Роль математических компетенций студентов в изучении ими дисциплин профессионального цикла

Развитие общества немыслимо без формирования и развития математической компетентности его членов. Математическая подготовка является полноправной и важной составляющей среднего профессионального образования (СПО). Она в образовательных учреждениях среднего профессионального образования (ОУ СПО), ведущих подготовку специалистов среднего звена, осуществляется в соответствии с требованиями Государственного образовательного стандарта среднего профессионального образования (ГОС СПО). Разноуровневое изучение математики на 1–3-м курсах создает фундамент, необходимый для формирования и развития общих и профессиональных компетенций, воспитывает математическую культуру, способствует осознанию значения математических компетенций в различных сферах профессиональной деятельности.

Актуальной остается проблема эффективной реализации межпредметных связей общеобразовательных дисциплин между собой и с дисциплинами профессионального цикла. Например, при изучении геометрии понятие «вектор» тождественно для студентов понятию «направленный отрезок», причем все направленные отрезки, имеющие одинаковую длину (модуль) и направление, понимаются как один и тот же вектор. Для нужд же физики и технической механики такое недифференцированное понимание оказывается недостаточным, поэтому вводятся уточнения: «свободный вектор» (направленный отрезок, характеризующийся лишь длиной и направлением; так понимают векторы при преподавании геометрии); «скользящий вектор» (характеризуется не только длиной и направлением, но и прямой, которой принадлежит; все направленные отрезки одинаковой длины и направления, принадлежащие одной прямой, понимаются как один и тот же скользящий вектор); «связанный вектор» (характеризуется длиной, направлением

и точным указанием начала; два направленных отрезка одинаковой длины и направления, но начинающиеся в разных точках – это два разных связанных вектора). Далеко не каждый студент сразу сообразит, что «свободный вектор», о котором говорит преподаватель физики или технической механики,– это тот же самый «вектор», о котором говорил преподаватель математики. Подобных «разночтений» в понимании сущности фундаментальных математических понятий преподавателями математики и педагогами, преподающими обеспечиваемые математикой дисциплины, имеется, к сожалению, множество [5].

Поэтому очень важным является осмысленное приложение базовых математических компетенций к решению образовательных задач, возникающих при изучении студентами ОУ СПО дисциплин профессионального цикла. По нашему мнению, основная функция преподавателей математики, состоит в «вооружении» студентов основами математических знаний и умений в объеме, необходимом в их повседневной жизни, в практической деятельности, в сознательном усвоении дисциплин профессионального цикла. Объем этот должен быть достаточен и в контексте дальнейшего самообразования.

Важным достоинством рассматриваемых нами далее математических заданий является их прикладная направленность. Они направлены на формирование у обучающихся навыков построения и исследования математических моделей реальных процессов, они способствуют развитию логического мышления, стимулируют творческий подход к поиску решения. У студентов формируется и развивается умение оценивать полученный результат, прогнозировать исход изучаемой ситуации (физического эксперимента), сравнивать, анализировать, контролировать правильность полученных выводов, оценивать степень их обоснованности и тому подобное.

Иногда обучающиеся не осознают необходимость математических знаний и умений в обучении выбранной специальности. Их тревожит разнообразие изучаемых математических понятий: логарифмы, показательная функция, тригонометрические функции, пределы функций, производные функций, неопределенные и определенные интегралы, дифференциальные уравнения. Обучающимся не вполне понятно, действительно ли при работе на предприятии, в банке, в бухгалтерии, в офисе все эти понятия будут использоваться. Студенты сомневаются в том, что они способны качественно усвоить такой большой объем учебного материала.

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Рассмотрим пример. Обучающиеся выполняют задания контрольной работы по теме «Показательная и логарифмическая функции»: строят графики, решают уравнения и неравенства, потенцируют и логарифмируют выражения. Если решение математически верно, студент получает положительную оценку, действуя в том же духе далее, успешно сдает промежуточную или итоговую аттестацию, обретает право на получение стипендии. К сожалению, для многих студентов такой, хотя и положительный, но все же внешний, мотив при изучении математики становится доминирующим. Иначе обстоит дело при изучении дисциплин профессионального цикла, например, дисциплины «Программирование». Обучающийся добивается от программируемого им автомата не просто выполнения абстрактных функций и достижения отвлеченного результата. Студент получает удовольствие и удовлетворение, осознавая, что его деятельность принесет практическую пользу. В связи со сказанным мы полагаем, что занятиям математикой и содержанию математических заданий следует придавать такое содержание, которое позволяло бы достигать доминирования в мотивации учения студентов внутренних положительных мотивов.

Для развития интереса студентов к математическим дисциплинам преподавателю ОУ СПО необходимо учитывать ведущие группы мотивов учения: интерес к знаниям, к процессу их приобретения, осознание теоретической и практической значимости изучаемого материала, стремление к достижению успеха при выполнении заданий прикладного характера.

Решение прикладной задачи начинается с построения ее математической модели. Вообще, алгоритм математического решения прикладной задачи таков:

• -    дана прикладная задача - техническая, экономическая (вообще говоря, предметная, содержательная) модель какого-либо реального объекта, процесса, явления;

• -    на основании данных прикладной задачи выполняется построение ее математической модели (строится математическая интерпретация данных исходной задачи);

• –   для математической задачи выбирают (а если не из чего выбирать,

то и разрабатывают) метод решения ;

• -   метод решения реализуется путем осуществления процесса решения,

выполнения шагов алгоритма решения математической задачи;

– полученному математическому решению (результату) дается техническая, экономическая (вообще говоря, предметная, содержательная) трактовка.

Как видим, обучающийся должен уметь строить и анализировать математические модели, выбирать методы решения, обосновывать результаты. Поле деятельности не ограничивается при этом изучением именно математики. Например, для студентов специальности «Автоматизация технологических процессов и производств» обладание развитыми математическими компетенциями актуально при освоении следующих дисциплин:

– ОП.02 Электротехника: решение квадратных систем линейных алгебраических уравнений (например, методом Крамера) при расчете по правилам Кирхгофа сил постоянного тока в сложных электрических цепях с заданным значением электродвижущей силы; построение синусоидальных кривых и изображающих их комплексных чисел (векторов) по уравнению зависимости гармонических колебаний электрических характеристик цепи переменного тока; расчет характеристик цепей переменного тока с использованием комплексных чисел и гармонических функций комплексного переменного; разложение периодической функции в ряд Фурье при исследовании несинусоидальных токов.

– МДК.01.01 Технология формирования систем автоматического управления типовых технологических процессов, средств измерений, несложных мехатронных устройств и систем, МДК.01.03 Теоретические основы контроля и анализа функционирования систем автоматического управления: применение дифференциальных уравнений при описании электрических цепей, при составлении передаточных функций, при изучении устойчивости систем; применение интегрального исчисления при описании динамических звеньев.

– ЕН.03 Информационное обеспечение профессиональной деятельности, ОП.07 Электронная техника, ОП.08 Вычислительная техника: решение с применением математико-ориентированных компьютерных систем алгебраических уравнений и их систем, вычисление пределов функций, определенных интегралов, построение графиков функций; путем программирования в интегрированных средах разработки программного обеспечения выполнение расчета серии значений функции на указанном промежутке и так далее.

Кроме того, все студенты ОУ СПО изучают в большем или меньшем объеме те или иные экономические дисциплины, где математическое моделирование и исследование предметной области (вычисление производительности труда,

себестоимости продукции, заработной платы и тому подобного) часто сводится к анализу математико-графических объектов.

Пример типичной задачи: зависимость измеряемой в рублях стоимости перевозки груза (обозначим ее y ) от измеряемой в километрах дальности перевозки (она обозначена x ) для каждого из трех видов транспорта задается формулами:

y^lO+lOx, v2=20+^x, v3=30+5x.

Используя графический метод, требуется определить: вид транспорта, обеспечивающий наименьшую стоимость перевозки при дальности 200 км, 300 км, 450 км; из первого и второго видов транспорта выбрать тот, перевозка груза которым экономически более выгодна при дальности 400 км.

При изучении дисциплин профессионального цикла студенты сталкиваются с необходимостью строить и читать графики различных видов, производить расчеты с применением графических методов (особенно это относится к студентам, осваивающим профессии и специальности технического профиля). Студенты должны правильно строить и читать графики различных функций для того, чтобы произвести ремонт оборудования, наладку или настройку аппаратуры, выбор режима реализации технологического процесса в соответствии с заданными техническими условиями. Существуют задачи на построение графиков выпуска продукции в определенных экономических условиях, исследование динамики экономических показателей в результате модернизации производства, оценку показателей эффективности использования средств, израсходованных на совершенствование технологического процесса и так далее. Такого рода задачи приводятся зачастую к трудным для решения аналитическими методами системам уравнений и неравенств (иногда сопровождаемых дополнительными требованиями, например, требованием достижения экстремальных значений одной или несколькими целевыми функциями) [4]. Такие задачи тогда можно решать графическими методами, являющимися к тому же, инструментом реализации дидактического принципа наглядности в обучении [3].

Студенты специальностей «Сети связи и системы коммутации» и «Информационная безопасность телекоммуникационных систем», изучая дисциплины

профессионального цикла, производят расчеты с использованием графического метода по темам «Составляющие прямоугольных импульсов», «Прохождение сигналов через нелинейные цепи», «Нелинейные характеристики диодов, транзисторов», «Спектральное представление сигналов» и так далее. Студенты специальности «Банковское дело» решают (и не только графическими методами) экономические проблемы, приводящие к задачам линейного программирования (поиску точки n -мерного линейного пространства, в которой достигает экстремума (оптимального значения) линейная форма n переменных, на значения которых наложены ограничения, являющиеся равенствами или неравенствами, с левыми частями, представленными линейными формами, и правыми частями, представленными действительными числами) [1; 2].

При решении многих задач экономического содержания используются элементы теории матриц. Объясняется это тем, что довольно большое количество экономических объектов и процессов в математической форме именно с помощью матриц представляется наиболее просто и компактно.

Актуальными для студентов ОУ СПО некоторых специальностей и профессий являются также математические компетенции, связанные с арифметикой и алгеброй комплексных чисел, с элементами теории функций комплексного переменного. В современной компьютерной технике не только на программном, но в некоторых случаях и на аппаратном уровне используется комплекснозначная арифметика. Интересны комплексные числа и студентам специальности «Экономика и бухгалтерский учет». Вообще, в современных экономических исследованиях комплекснозначные величины находят все большее применение. Например, качество товара может быть представлено комплексным числом Т = П + iЦ , действительная часть которого П является интегральной числовой характеристикой потребительских свойств товара, а мнимая часть Ц есть числовая оценка его рыночной стоимости, цена товара ( i – мнимая единица, i² = -1 ).

Мы полагаем, что при изучении математики следует предлагать студентами решать как можно большее число прикладных задач, связанных с их будущей профессией, специальностью. Преподаватель математики может подбирать и составлять такие задачи в сотрудничестве с преподавателями дисциплин общепрофессионального и профессионального циклов. Приведем конкретные примеры.

При изучении линейной алгебры (тема «Решение систем линейных алгебраических уравнений»; применяются методы Крамера, Гаусса, обратной матрицы) можно обратить внимание обучающихся на слова академика П.С. Александрова, отмечавшего огромное

значение в системе обучения математике уравнений как средства познания природы: «Составление уравнения есть основной прием, посредством которого математика применяется к естествознанию и технике. Без уравнения нет математики как средства познания природы». Затем уместно предложить задачу: изучая сложную электрическую цепь постоянного тока с заданными электродвижущими силами, обозначая силы токов в ветвях цепи буквами I 1 , I 2 , I 3 и применив правила Кирхгофа, исследователь получил следующую систему линейных алгебраических уравнений:

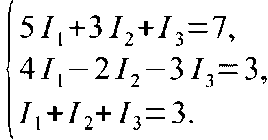
Найдите силы токов I 1 , I 2 , I 3 .

При изучении математического анализа (тема «Комплексные числа») можно предложить задачи, данные ниже.

• 1.    Найдите силу переменного тока, протекающего через участок цепи, если напряжение между его концами и импеданс (комплекснозначное сопротивление) таковы:

  

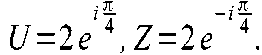
первого вектора и модуль второго вектора измерены соответственно в амперах и вольтах. Найдите импеданс (комплекснозначное сопротивление) обмотки, воспользовавшись законом Ома для участка цепи.

Студентам экономических специальностей при изучении линейной алгебры (тема «Матрицы и действия над ними») могут быть интересны прикладные задачи подобные следующей: по данным таблицы 1 выполните расчет суммарной заработной платы, выплачиваемой предприятием работникам, при выполнении каждого из заказов Зак 1 , Зак 2 , Зак 3 . В каждом из заказов нужно изготовить и отпустить заказчику в заданных количествах и ассортименте изделия видов А, В, С. Производство продукции осуществляется на пяти рабочих местах РМ 1 , РМ 2 , РМ 3 , РМ 4 , РМ 5 , для которых известна заработная плата, выплачиваемая работнику за час работы и затраты труда на единицу продукции.

Таблица 1. Данные сформулированной выше задачи с экономическим содержанием

Виды изделий	Затраты труда на рабочих местах (часов на одно изделие)					Количество изделий
	РМ,	РМ2	РМ3	РМ4	РМ5	Зак,	Зак2	Зак3
А	2	1	4	5	0	0	0	5
В	1	4	2	5	2	4	2	1
С	0	1	0	3	4	2	4	0
Часовая зар. плата (руб.)	1,25	1,50	1,40	1,40	1,25

Необходимость обладания математическими компетенциями сопровождает студента ОУ СПО в течение всего срока обучения. Не является исключением период подготовки и защиты дипломной работы. В практике автора имеется позитивный опыт, связанный с вышесказанным. Студенты-дипломники специальности «Программирование в компьютерных системах», консультируемые преподавателями математики, работали над созданием программных оболочек «Комплексные числа», «Элементы линейной алгебры». При защите названные дипломные проекты получили положительные отзывы, а разработанные программные оболочки были рекомендованы ко внедрению в образовательный процесс.

t^CCtH»*

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Например, задачей дипломного проекта «Решение экономических задач с применением матричного исчисления» было создание программной оболочки, предназначенной для решения экономических задач методом матричных вычислений с возможностью добавления в функционал программы средств реализации дидактического тестирования обучающихся.

Проект был реализован поэтапно. Для проверки корректности выводимых данных, корректности ввода, правильности выполнения логических операций и тому подобного программа была протестирована на типовых и критических значениях, на заведомо некорректных или ошибочных входных данных, на способах ввода-вывода, приводящих к системным ошибкам (ошибки чтения файлов, несоответствие файловых форматов). Тестирование подтвердило полную работоспособность программы, ее верную функциональность и соответствие поставленному техническому заданию.

Программа распространяется в самораспаковывающемся архиве. Продукт сопровождается интерактивной гипертекстовой справочной системой. Пользователь-студент может выбрать тип задачи из числа предложенных и ввести конкретные числовые данные. Чтобы увидеть решение, после ввода данных необходимо нажать кнопку «Показать решение». После ее нажатия возникнет форма с запросом пароля. Без ввода пароля студент не сможет увидеть правильных ответов, поэтому сначала преподаватель должен проверить решение, выполненное студентом «вручную». Потом будет введен пароль и результат, полученный студентом, можно сравнить с выводом программы. Здесь преподаватель может поставить студенту оценку за решение расчетной части комплексного задания.

После оценивания расчетной части студент может закрыть программу (если теоретическую часть он уже сдал устно) либо перейти к дидактическому тестированию. Пройдя тест, студент сможет увидеть краткий анализ своих результатов.

В заключение отметим: результатом изучения студентами ОУ СПО математики как отдельной дисциплины, широкого применения и развития математических компетенций при освоении дисциплин профессионального цикла должно стать осознание обучающимися того, что область приложений математики является неограниченной, что математические объекты, понятия и факты суть необходимый фундамент для изучения естественно-научных дисциплин и дисциплин профессионального цикла. Каждый член современного общества должен быть математически грамотным.