Роль вариационных принципов механики в исследовании эволюции неконсервативных динамических систем

Мопертюи ( 1698-1759 ) предложил универсальную гипотезу, согласно которой любые события в природе описываются при помощи определенной величины, называемой действием , принимающей минимальной значение на истинном пути движения. Однако Мопертюи не смог четко определить величину, которая должна быть минимизирована.

Эйлер (1707-1783) внес существенный вклад в развитие теоретической механики, свои работы в области вариационной механики он начал с изучения «изопериметрических» задач, для которых нашел решение в явном виде. Хотя Эйлер и не сформулировал четкого принципа наименьшего действия, что было впервые сделано Лагранжем, его применения этого принципа к механическим задачам, по сути дела, эквивалентны лагранжевой явной формулировке.

Лагранж (1736-1813). Если принцип виртуальных перемещений и принцип Даламбера позволили рассматривать механическую систему как нечто целое, не разбивая ее на изолированные частицы, то уравнения Лагранжа добавили еще одно важное свойство – инвариантность относительно произвольных преобразований координат. Лагранж создал инструмент решения механических задач при помощи чистых вычислений, без каких бы то ни было физических или геометрических соображений, при условии, что кинетическая и потенциальная энергии заданы в аналитической форме. Метод использования дополнительных условий при помощи неопределенных множителей – открытие Лагранжа, которое играет важную роль в теоретической механике.

Гамильтон ^(1805-1865) . Уравнения Лагранжа были довольно сложными дифференциаль ными уравнениями второго порядка. Гамильтон сумел преобразовать их в систему дифференциальных уравнений первого порядка с удвоенным числом переменных, позиционные координаты и импульсы рассматривались при этом как независимые переменные. Это простейшая и наиболее удобная форма, к которой могут быть приведены уравнения вариационной задачи, получившей название «канонические уравнения», данное им Якоби. Гамильтон, преобразовав принцип Даламбера, впервые дал точную формулировку принципа наименьшего действия. Форма, в которой применяли этот принцип Эйлер и Лагранж, справедлива лишь для консервативных (склерономных) систем.

Принцип наименьшего действия (стационарности действия) является фундаментальной основой лагранжевой и гамильтоновой формулировок механики. Не все физические системы имеют уравнения движения, которые можно получить из этого принципа, однако все фундаментальные взаимодействия ему подчиняются, в связи с чем этот принцип признан одним из ключевых положений современной физики. Получаемые с его помощью уравнения движения имеют название уравнений Эйлера — Лагранжа.

При исследовании одномерного механического движения принцип стационарности действия записывается в форме функционала движения [2,3]:

S[x(t)] = J L(x(t ),5 & (t),t)dt ^ expr ,                                       (1)

t 0

где Ц ) = df .

Наша задача - нахождение истинного закона движения x = x ⁰( t ), удовлетворяющего уравнению (1). Решением данной задачи является решение классической задачи функционального анализа о «траектории с закрепленными концами».

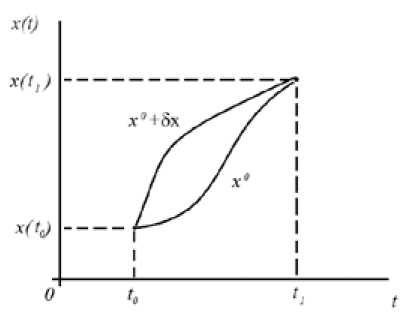
Рис. 1. Графическое представление траектории с закрепленными концами

Графически данную задачу можно представить в виде графика (рис. 1).

Из всего многообразия функций х = х ( t ) истинным будет тот закон, который удовлетворяет условию ⁽¹⁾ при движении из точки х ⁽ t 0 ) в точку ^{х (} t 1 ).

Любой неистинный закон будет отличаться от истинного закона на величину 8х = 8х(t) и будет иметь вид х = х0 (t) + 8х(t),                                                      (2)

где ^{8 х (} t ) ^- произвольная функция.

Отклонение от х0 (t) на величину 8х(t) будет приводить приращению функционала (1), которое составит t1

A S [ х ⁽ t ^)] = J L ⁽ x ⁰ + 5 x , x ⁰ + 3 x, t ) ^- L ⁽ x ⁰, x ⁰, t ) dt .

t 0

В уравнении (3) функция 8 х ( t ) = х ( t ) - х ⁰ ( t ) является вариацией аргумента функционала

(1). На границах истинной траектории выполняется условие

8 х(t о ) = 0 ,                                                                           (₄

⁸ x^(t i ) = °

Подынтегральная функция уравнения (3) может быть разложена по формуле Тейлора (5):

I

A L = dL + — d² L + ••• 2 /

Линейная часть приращения функции L описывается первым дифференциалом dL :

dL = — ( L ( x ⁰ + 5 x , x ⁰ + 5 x, t ) - L ( x °, Xc °, t )).

dt dt

Определим производные:

б)

d L

d L Г d x d

-----1 I + d x (5 t J

d L Г d x | d x 15 t J ’

_ дL  дL Sx  дL Sx а-б) — =--+--.

д t   дx д t   дx д t

С учетом (7) выражение (3) примет вид dLs 8L^

A S I x ( t ) l = (— 8x + &) dt .

i d x 6 x

Целью решения задач вариационного исчисления является поиск дифференциального уравнения, удовлетворяющего условию (1), для этого применяется основная лемма вариационного исчисления. При получении уравнения (8) лемма применяется при выносе за скобки общего множителя 8 X и 8 X .

Проинтегрировав по частям второе слагаемое уравнения (8), получим условие выполнения равенства (1):

• ^{4 5} [ * ¹ 1 > 1=) \т - d ¹ d L > V» = , 15 x dt 6x )

  
  

С учетом основной леммы вариационного исчисления условие (9) примет вид dL

8 x

d ( dL d dt (ax J

= 0.

Выражение (10) называется уравнением Эйлера – Лагранжа. Уравнение (10) также можно получить, применив лемму Дюбуа – Реймона.

Рассматривая поведение функции L относительно преобразований координат, можно по

^, лучить ряд инвариантов механической системы. Одним из таких инвариантов является полная механическая энергия консервативной системы.

Полная производная функции L ( x ( t ),, x ( t ), t ) по времени имеет вид (при условии, что она не зависит явно от времени)

dL дL дx дL дX

— = ——+ — — . dt   дx д t дx д t

С учетом (10) уравнение (11) примет вид

dL  d (8 L Y d L

— = —I — l x +-- x .

dt dt Vc)xc J    d xc

Уравнение (12) представляет собой производную произведения функций ∂L и по времени, dX следовательно,

dL d ( a L ) .a L d (8L Y — = —I — I x + x = —I — x I. dt dt dd x:) d x: dt d d x )

Уравнение (13) можно переписать в виде

a l

Из уравнения (14) видно, что величина E = —x - L, называемая энергией, остается посто-дx янной во времени.

Если ввести обозначения

dL-n д x p ^,

5L = f

9x     ’ где p – обобщенный импульс; f – обобщенная сила, то уравнение энергии примет вид

E = px - L .

Закон движения материальной точки под действием сил, зависящих от простран-w                                                     w                                 тт ственной координаты и её скорости, описанный с помощью уравнения Ньютона, имеет вид

mx + n ( x ) x = ф ( x ),

где m - масса материальной точки; n ( x ) - коэффициент трения, зависящий от координаты;

dП

^ ( x ) =---возмущающая потенциальная сила.

dx

Запишем уравнение Лагранжа второго рода для данной механической системы:

d дк дк   дn  , . d к

^{n ( x} , dt д x   д x     д x       д x

где

K = —

.

Умножим обе части уравнения (17) на неизвестную функцию ц и представим его в следующем виде:

d д K      . ,9K   д . _v

^- — + ц- п ⁽ x )— = —⁽ p K ^- р П) . dt д x           д x    д x

Определим вид функции μ таким образом, чтобы левая часть уравнения (18) представляла собой производную по времени от произведения двух функций:

d ( д K )

—I ц — I = Ц dt\    д x J

d д K ₊ d ц д K dt д x dt д x:

d д K dt д x

d д

+ ц n ( x )— = — —⁽ ^ K ^- у П ) .     ⁽²¹⁾

д x   dt д )&

Из уравнения (19) видно, что dy

— = у n ⁽ x ).

dt

⁵ K - 1

Разделим обе части уравнения (22) на р и, умножив на dt --, проинтегрируем: 8 x

J -^-/n (,) dt = b« - n (x) t.(23)

Выразив из (21) μ, получим

Ц = e"(-) t.(24)

С учетом уравнений (20), (21) и (24) имеет место равенство

— (pK - цП) --—(pK - МП) = 0.(25)

8 x^      dt 8 x^

Уравнение (25) соответствует уравнению Эйлера (10). Таким образом, функция Лагранжа рассматриваемой механической системы имеет вид

L = (K - П)p

При этом действие такой системы описывается уравнением t1

S[x(t)] = J(K(x) - П(x))p(x, t)dt ^ extr.

t ₀

Ковариантность уравнения (25) относительно замены координат и знание вида Лагранжиана (26) позволяет получать уравнения движения в удобной для решения форме, исследовать эволюцию динамических систем с линейным трением, а также определить преобразования симметрии и соответствующие им инварианты с применением теоремы Нётер.

Законы сохранения имеют глубокое происхождение, связанное с инвариантностью описания механической системы относительно некоторой группы преобразований времени и координат. Согласно теореме Нётер, каждой непрерывной симметрии физической системы соответствует некоторый закон сохранения. Симметрия - соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях. Рассматривая различные преобразования координат, мы приходим к основным физическим симметриям [4].

При рассмотрении движения механической системы в пространстве могут быть использованы преобразования координат вида (28).

Таблица 1. Симметрия в физике

Преобразование	Соответствующая инвариантность	Соответствующий закон сохранения
Трансляция времени	Однородность времени	энергии
	Изотропность времени	четности
Трансляция пространства	Однородность пространства	импульса
Вращение пространства	Изотропность пространства	Момента импульса
Группа Лоренца	Относительность Лоренц-инвариантность	4-импульса
Калибровочное преобразование	Калибровочная инвариантность	заряда

t = f/t, x, a)                                               рю ((i = !,2, K, П) ,                                             (28) Ix, = ft (t, x, a) где a – независимый параметр.

Если рассматривать значения параметра а достаточно близкими к нулевым, то преобразования (26) можно представить в виде

■	\t * , f “( / ’ л )( i = 1,2, K, n ) .                                              (29) I xf = f i^ ( t, x , A a )

В результате разложения в ряд Тейлора преобразований (29), ограничиваясь членами, линейными относительно А а , получают бесконечно малые преобразования, которые можно записать в виде

•	* */Л           A (i = !’2’ K ’ П ) .                                                (30) t xi(t ) = xAt ) + A x

Например, возможные параллельные переносы трехмерной системы координат описываются преобразованием

J	* t t ( i = 1,2,3) .                                                       (31) q i = q i + a i

А бесконечно малое преобразование при этом имеет вид

■	\ t * = t I q * = q i + ^'- 1,2,3) .                                                (32)

Совокупность всех вращений декартовой системы координат на плоскости описывается преобразованием

‘	*            t = t X = X . cos( a ) - y . sin a ) .                                           (33) . y =- X • sin( a) + y • cos( a a

А его бесконечно малое преобразование таково:

* t ='

• 1    ^X = ^{X - е}-y .

У * = У - £• X

Преобразования (30) называются преобразованиями симметрии, если выполняется условие инвариантности действия относительно этих преобразований. Данное условие имеет вид:

t1                                     t1                         **

I L(x, x, t)dt = I L1(x, x, t )dt ,(35)

* t0

где функция L 1 - некоторая другая функция Лагранжа, позволяющая получить те же уравнения движения, что и L.

Одним из следствий теоремы Нётер является уравнение первого интеграла движения, который с использованием функции Лагранжа описывается следующим уравнением:

n

LAt + У —+. +АЯ = А C, : dx '

где 5x, = Ax — xAt, а АХ — функция, определяемая из уравнения дL хdL .   , ■n дL         d d , .

— A t + / —Ax i + / — Ax i + L — A t —--(AA).

д t        i _— 1 д x        i _— 1 д x          dt dt

Уравнение (37) применяется в качестве критерия для выяснения, является ли (28) преобразованием симметрии для исследуемой системы.

В качестве примера использования теоремы Нетер и функции Лагранжа на практике рассмотрим колебательную системы с силой трения, линейно зависящей от скорости и не зависящей от координаты. Лагранжиан такой системы с учётом (26) и (24) будет иметь вид

L = ( К - П) , = ⁽2 mx- - 2 cx ■ > e nt .

Обозначив

2в = n, k2 = c/m(39)

лагранжиан представим в виде

Уравнение движения такой системы имеет вид x + 2px + k2 x = 0.(41)

Преобразованием симметрии такой системы будет преобразование вида

*

t = t + £

"

I x = x - ^{£в х}

Действительно, учитывая, что А t = е, А x = -ев x , A x = -в х из уравнения (37) получаем

Δλ = 0, а из уравнения (36) – первый интеграл системы:

1 &  2      1 7 2 2 О &  | 2 pt

• 2    ^{х +} 2 ^{х + хх} у       .

'

Решение уравнения (39) можно представить в виде графика (рис. 2)

Для интерпретации физического смысла первого интеграла (43) рассмотрим во времени графики слагаемых первого множителя уравнения (43) и самого интеграла (рис. 3).

Таким образом, интеграл (41) играет ту же роль, что и интеграл энергии для консервативной системы.

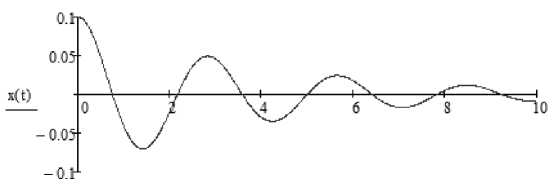
Рис. 2. Эволюция динамической системы с линейным трением во времени

Рис. 3. Эволюция первого интеграла во времени и его компонентов:           – потенциальная энергия,

– кинетическая энергия,           – работа сил трения

Первые интегралы движения имеют в механике большое значение. Даже в тех случаях, когда уравнения движения оказываются неинтегрируемыми, знание первых интегралов позволяет представить физическую картину изучаемого движения. Известные законы сохранения количества движения, кинетического момента, механической энергии системы являются первыми интегралами уравнений движения.

Исключительная общность вариационных принципов механики, возможность сравнительно простого их обобщения на многочисленные области физики, их связь с законами сохранения ставят эти принципы в центральное положение при решении многих фундаментальных проблем физики.

Как мы увидели выше, для учета диссипативных сил при исследовании динамической системы возможно определение функции Лагранжа такой системы и нахождение ее инвариантов. Все это помогает наиболее полно представить физическую картину изучаемой системы.