Рождение оптических вихрей при распространении поля с начальным дробным топологическим зарядом

Основными характеристиками лазерных вихревых пучков [1] являются топологический заряд (ТЗ) и орбитальный угловой момент (ОУМ). Топологический заряд оптического вихря (ОВ) формально определён Берри в [2], а ОУМ был введён в оптику в [3]. Если полный ОУМ параксиального светового поля сохраняется при распространении в свободном пространстве, то ТЗ сохраняется не всегда. Топологический заряд сохраняется при распространении, если амплитуду начального светового поля можно описать в факторизованном виде E ( r , ϕ ) = A ( r ) exp( in ϕ ), где A ( r ) – составляющая амплитуды, зависящая только от радиальной переменной r , ϕ – азимутальный угол, n – целое число, топологический заряд ОВ. Примерами таких световых полей являются хорошо известные пучки Бесселя–Гаусса и Лагерра–Гаусса. Примеры несо-хранения ТЗ при распространении ОВ можно найти в работах [4–9]. В [4] рассмотрена простая суперпозиция Гауссова пучка и моды Лагерра–Гаусса (ЛГ) с

номером (0, n), причём радиусы перетяжки у Гауссовых пучков разные. Из-за разной расходимости в комбинированном пучке при распространении в пространстве изменяется ТЗ. Если в начальной плоскости радиус перетяжки Гауссова пучка больше радиуса перетяжки моды ЛГ, то ТЗ комбинированного пучка сначала равен нулю. По мере распространения радиусы обоих пучков выравниваются, и после этой плоскости радиус моды ЛГ становится больше, чем радиус Гауссова пучка. С этого места ТЗ комбинированного пучка становится равен n. В [2] теоретически, а в [5, 6] экспериментально показано, что Гауссов пучок с начальным дробным ТЗ при распространении в ближней зоне имеет целый ТЗ, равный целому числу, ближайшему к дробному числу. То есть если начальный дробный ТЗ равен µ = n + ε (ε < 1/2), то ТЗ пучка равен n. Если начальный ТЗ равен µ = n + ε (1/2 < ε < 1), то ТЗ пучка равен n + 1. Но оказалось, что при дальнейшем распространении таких пучков их ТЗ претерпевает и другие изменения, ранее не известные. Так, в [7] численно и экспериментально показа- но, что в зоне Френеля ТЗ Гауссова оптического вихря с начальным дробным ТЗ равен целому числу на единицу большему, чем ближайшее целое число к начальному дробному ТЗ. То есть если начальный дробный ТЗ равен ц=n + s (0,1 < s < 1), то ТЗ пучка равен n +1. Хотя в [7] есть неточности. Начальный пучок задан в виде rц exp(-r2/w2 + iцф), и его Френель-образ должен быть пропорционален функции Куммера, зависящей от числа ц. Но в [7] нет функции Куммера. Аналогичное исследование провели авторы работы [8]. В [8] действительно ТЗ измеряется в Фурье-плоскости (в фокусе сферической линзы) и получены результаты, отличные от результатов работы [7]. В [8] показано, что ТЗ Гауссова оптического вихря exp(-r2/w2 + iцф) с дробным начальным ТЗ ц = (2к + 1) + s (0,1 < s < 1) в дальней зоне равен 2k + 1. А если начальный дробный ТЗ равен ц = 2к + s (0,1 < s < 1), то в дальней зоне равен ТЗ также 2k + 1. Эти исследования показали, во-первых, что ТЗ не всегда сохраняется при распространении, а во-вторых, что чётные и нечётные ТЗ по-разному ведут себя при распространении. Это следует из того, что какой бы дробный начальный ТЗ не был (близкий к чётному целому или близкий к нечётному целому), в дальней зоне ТЗ будет всегда целым нечётным числом.

Заметим, что измерять ТЗ можно с помощью треугольной диафрагмы [10, 11] или цилиндрической линзы [12].

Заметим также, что оптический вихрь может находиться на периферии распределения интенсивности лазерного пучка, там, где интенсивность очень мала. Обнаружить экспериментально такой ОВ затруднительно, если вообще возможно. Но при расчёте по формуле, которая определяет ТЗ, такой ОВ учитывается, и величина ТЗ зависит от этого вихря. В численном эксперименте результат расчёта величины ТЗ зависит от радиуса окружности, по которой суммируют градиент фазы светового поля. Поэтому правильного результата расчёта ТЗ следует ожидать, когда согласуются все три составляющие: расчёт по формуле [2], расчёт по модельным картинам фазы поля и экспериментальное определение ТЗ [10–12].

В данной работе мы теоретически и численно рассматриваем эволюцию Гауссова ОВ с начальным дробным ТЗ и фактически объединяем результаты работ [2], [7] и [8]. Мы показали, что имеется всего 4 возможных варианта эволюции ОВ с начальным дробным ТЗ. Мы показали, что в [2, 5, 6] измеряли ТЗ в ближней зоне, в работе [7] – в зоне Френеля и в [8] – в дальней зоне.

Как правило, при распространении ОВ в атмосфере в присутствии турбулентности для идентификации ОВ измеряют ОУМ [13, 14]. Но из-за малых «дрожаний» всего пучка и его составных частей ОУМ непрерывно изменяется. Хотя при слабой турбулентности он изменяется слабо, а при сильной – сильно. Если измерять ТЗ, то он может изменяться только дискретно, остава-

ясь целым. Поэтому при слабой турбулентности ТЗ вообще не должен изменяться. Мы показали с помощью дифракции ОВ на случайном фазовом экране, что ТЗ остаётся неизменным вплоть до существенных искажений величины случайной фазы экрана.

1. Теория

Топологический заряд рассчитывается с помощью формулы, предложенной Берри [2]:

TC = lim 1 f d ф A arg E ( r , ф ) = r н- да 2 п 0    дф

1 lim _т ²r , d E ( r , ф ) / дф

=--Im dф--———.

2 п r ^ да    0       E ( r , ф )

Амплитуда Гауссова пучка с начальным дробным топологическим зарядом имеет вид [2]:

E ( r , ф , z = 0) = exp

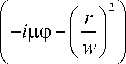
e in ф- r ² / w ²

e* ^пц sin пц

п

да

I n=-да

ц- n

Амплитуда поля (2) в зоне Френеля выражается через разность модифицированных функций Бесселя [15]:

E (p, 9 , z ) = J— | —— |expf^5- + i пц1х ⁽ ) qz J 4 2 z      J

x sin ( пц ) V x exp ( - x ) x

да x I (-i)

m =-да

exp ( im 9 ) ц- m

I m H ( x ) - 1 | m H ( x )

где x = ( z 0 / z )²( p / w )²/(2 q ), q =1- i ( z 0 / z ), I v ( x ) - модифицированная функция Бесселя.

В «ближней зоне» z <<  z 0 параметры в (3) принимают вид: x = ik p ²/(2 z ), q = - i ( z 0 / z ). И так как модифицированная функция Бесселя и обычная связаны известным соотношением

I _v ( ix ) = i ^v J _v ( x ),

то получаем в ближней зоне [2, 15]:

A A 1       f ik p²_u- 1

E ( p , 9 , z ) = ,— exp I---- + i пц lx

V 2 п    ( ² z      )

x sin ( пц ) .Jty exp ( - iy ) x

( -A m e im ⁹

^x I ( - i ) ----- m =-да ц- m

i ^{(| m | 1)/2} J Im | - 1 ( y ) - iJ Im | + 1 ( y ) ,

где y = к p ²/(2 z ). В пределе при p ^да, используя асимптотику функций Бесселя

J v ( y >>  1) «

y

vп

получим:

E(p ^ да,9,z) ®

Подставив (10) в формулу для расчёта топологического заряда (1), получим:

^

exp (i пц) sin (пц) п

да m=-да

exp (im 9) ц-m

Выражение (7) совпадает с (2) при w → ∞. Подставив (7) в (1), получим формулу для расчёта ТЗ в «ближней зоне»:

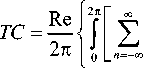
neinф ц-n

1-1

да ,nn ф

2 — d Ф^ .

n=-даЦ- n J

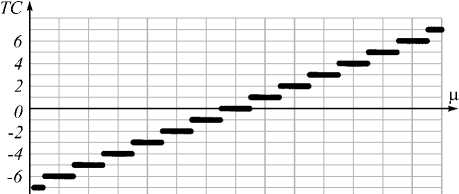
Расчёт по формуле (8) приводит к известной ступенчатой функции для ТЗ со скачками при ц = n + 1/2 (рис. 1). На рис. 1 показана зависимость TЗ Гауссова пучка с начальным вихрем с дробным ТЗ (2) в «ближней зоне» ( z <<  z 0 ), рассчитанного по формуле (8) для -7 <  ц < 7 с шагом 0,05, от величины начального дробного ТЗ ц .

-6     -4     -2      0      2      4      6

Рис. 1. TЗ Гауссова пучка с начальным дробным ТЗ, рассчитанный по формуле (8)

Как видно на рис. 1, скачки TЗ имеют место при полуцелых значениях, когда ц = n + 0,5, т.е. как описано в [2].

Рассчитаем далее ТЗ поля с начальным дробным ТЗ (2) в зоне Френеля. Для этого воспользуемся асимптотикой для модифицированной функции Бесселя при больших значениях аргумента:

In-1 (^)- In+1 (^) ~

e ^ 1Г 1 ( n - 1 ) 2 - 1

7м I     8^

ne ^

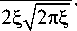
2 п

n 2 п

TC = Re 9

2п ,

да

e in ф

n =-да

да

n =-да

ц-n

e^ Ф

ц-n

dф >.

Рис. 2 показывает TЗ Гауссова пучка с начальным дробным ТЗ (2), рассчитанный в зоне дифракции Френеля по формуле (11) для 5 <  ц < 10 с шагом 0,05.

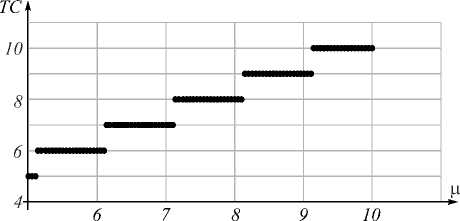
Рис. 2. TЗ Гауссова пучка с начальным дробным ТЗ (2) в зоне дифракции Френеля, рассчитанный по формуле (11)

Из рис. 2 видно, что скачки TC находятся вблизи каждого целого числа, когда ц ~ n + 0,1, как описано в [7]. Но в [7] утверждали, что такая зависимость для ТЗ имеет место в зоне дифракции Фраунгофера, а не Френеля. Но в [8] также, как в [7], исследовали ТЗ в дальней зоне (зоне дифракции Фраунгофера или в фокусе сферической Фурье-линзы) и получили другой результат.

В дальней зоне дифракции (в фокусе Фурье-линзы) амплитуда поля примет вид:

1 Г - iz , 1

E (р, 9, z )=             exp (i пц)хv 7 V2п I f хsin(пц) Vx exp(-x)x

.H exp(im< x2(-i)              Imb!(x)-iH;1 (x), m=-да          ц m 22

8^

Тогда получим с учётом асимптотики (9) вместо (3) следующее выражение:

E(р^ю,9,z) =

- iz 1I w I

z 0 Д p

Г ik р2 . )

exp I —— + i пц I sin ( пц ) х

”      mlexp (Im9)

^х т ²да ⁽ i )    ц- m ^H

где аргумент у функций Бесселя становится действительной величиной x = ( z o / f )²( p / w )²/2, f - фокусное расстояние линзы, формирующей дальнюю зону в плоскости фокуса. Расчёт ТЗ по формуле (12) и по формуле (1) приводит к ступенчатой функции, показанной на рис. 3. На рис. 3 показан TЗ Гауссова пучка с начальным дробным ТЗ (2) в дальней зоне дифракции, рассчитанный по формулам (12) и (1) для -5 <  ц < 5 с шагом 0,05.

Согласно рис. 3, скачки между соседними целочисленными значениями TЗ происходят при чётных целочисленных значениях, как описано в [8]. Из рис. 3 видно, что если начальный ТЗ целый ц = n , то он таким же останется в дальней зоне. Но слабые отклонения начального ТЗ от целого приводят к разным последствиям, в зависимости от того, чётное или нечётное это

целое число. Слабые отклонения начального ТЗ от нечётного целого числа не изменяют ТЗ в дальней зоне: он остается целым нечётным числом. Слабые отклонения начального ТЗ от целого чётного числа скачком изменяют ТЗ такого оптического вихря в дальней зоне. Если начальный ТЗ немного меньше чётного целого числа 2 m , то в дальней зоне ТЗ будет равен 2 m – 1. А если начальный ТЗ будет немного больше чётного числа 2 m , то в дальней зоне ТЗ будет равен 2 m + 1. Авторы пока не могут объяснить, почему происходит именно так.

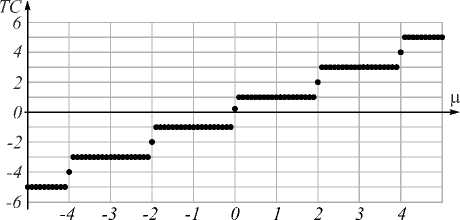
Рис. 3. TЗ Гауссова пучка с начальным дробным ТЗ (2) в Фурье-плоскости, рассчитанный по формулам (12) и (1)

Из рис. 1–3 следует интересная эволюция светового поля с начальным дробным ТЗ (2). Из рис. 3 видно, что в дальней зоне любое начальное дробное поле приводит только к нечётным ТЗ. Чётные ТЗ в дальней зоне можно сформировать, только если начальное поле будет иметь целый чётный ТЗ. Действительно, пусть в начальной плоскости ТЗ равен µ = 3,3. Тогда в «ближней зоне» сформируется ОВ с TC=3 (рис. 1), далее в зоне Френеля произойдёт рождение нового вихря с ТЗ +1, и ТЗ пучка станет равен TC=4 (рис.2). А в дальней зоне произойдёт рождение другого вихря с ТЗ –1, и ТЗ пучка опять станет TC=3 (рис. 3), как в «ближней зоне».

Иная эволюция у поля с начальным дробным ТЗ, близким к чётному целому числу, например, µ = 4,3. В «ближней зоне» у такого пучка ТЗ равен TC=4 (рис. 1), в зоне Френеля он равен TC=5 (рис. 2), и в дальней зоне ТЗ остаётся равным TC=5 (рис. 3).

Есть ещё два сценария эволюции поля с начальным дробным ТЗ, которые видны из табл. 1. В этой таблице приведены все 4 возможных сценария эволюции начального дробного вихря. Если простое начальное поле имеет целый ТЗ, то он сохраняется при распространении. Но если имеется линейная комбинация двух полей с разной расходимостью, то начальный целый ТЗ будет меняться [4]. В Приложении А приведён расчёт ТЗ комбинации двух оптических вихрей, обобщающий результат работы [4].

• 2.    Моделирование

• 3.    Эксперимент

Для подтверждения расчётов величины ТЗ по формулам (8), (11) и (12) в разных зонах дифракции Гауссова пучка с начальным дробным ТЗ было проведено моделирование. Распределения интенсивности и фазы в «ближней зоне» и зоне Френеля были получены BPM-методом (программа BeamProp фирмы

RSoft) при следующих параметрах: длина волны: λ =532 нм, радиус перетяжки Гауссова пучка w 0 = 5 λ (длина Рэлея в этом случае равна z R ~ 25 πλ ), полуразмер расчётной области: R = 50 λ , поперечный шаг дискретизации: Δ x = Δ y = λ /32, продольный шаг дискретизации: Δ z = λ /16. А распределения интенсивности и фазы в дальней зоне были получены с помощью преобразования Фурье, выполненного сферической линзой с фокусным расстоянием f = 100 мм для Гауссова пучка с радиусом перетяжки w 0 =0,5 мм, но с тем же начальным ТЗ. Начальный ТЗ был равен µ =3,3 (тип эволюции соответствует четвёртой строке табл. 1). Расчёт в ближней зоне был на расстоянии z =3 λ , а в зоне Френеля – на расстоянии z = 50 λ .

Табл. 1. Сценарии изменения ТЗ при распространении Гауссова пучка с начальным дробным ТЗ exp(–r²/w²)+i µϕ (p – произвольное целое число, 0<ε<1/2)

Начальный ТЗ z = 0	ТЗ в ближней зоне z <<  z 0	ТЗ в зоне Френеля z ≈ z 0	ТЗ в дальней зоне z >>  z 0
µ = 2 p + ε	2 p	2 p + 1	2 p +1
µ = 2 p – ε ,	2 p	2 p	2 p – 1
µ =(2 p + 1)+ ε	2 p + 1	2 p +2	2 p +1
µ =(2 p +1) – ε	2 p + 1	2 k + 1	2 p + 1

На рис. 4 показаны распределения интенсивности ( a , в , д ) и фазы ( б , г , е ) Гауссова пучка с дробным оптическим вихрем порядка µ =3,3 в «ближней зоне» ( z =3 λ ) ( a , б ), в зоне Френеля ( z = 50 λ ) ( в , г ) и в дальней зоне (в Фурье-плоскости сферической линзы с фокусным расстоянием f = 100 мм) ( д , е ). Стрелками на распределениях фазы показаны оптические вихри (центры сингулярностей) плюс первого порядка, а пунктирной стрелкой (на рис. 4 е ) показан оптический вихрь минус первого порядка.

Рис. 4 подтверждает результаты расчёта по полученным формулам (8), (11) и (12), которые отражены на рис. 1–3 соответственно. И подтверждает эволюцию ОВ, описанную в строке 4 табл. 1. Действительно, на рис. 4 б видно, что, хотя в начальной плоскости ( z =0) ТЗ был равен µ = 3,3, сразу же за начальной плоскостью (на расстоянии всего 3 λ ) у ОВ есть только 3 точки сингулярности (ТЗ равен 3). Хотя какие-то возмущения фазы с правой стороны на рис.4 б присутствуют, но разглядеть ещё точки сингулярности не удаётся. На рис.4 г на расстоянии 50 λ (длина Рэлея примерно 75 λ ) видно, что появилась четвертая точка сингулярности (это показывает сбой полос повыше трёх исходных точек сингулярности). Топологический заряд теперь равен 4. При дальнейшем распространении (в фокусе сферической линзы), как показано на рис.4 е снизу, появляется ещё точка сингулярности, но с обратным знаком (–1). И полный ТЗ пучка опять стал равен начальному 3.

Этот параграф посвящён изучению устойчивости ТЗ оптического вихря к фазовым искажениям. В нашем эксперименте мы исследуем сохранение целого ТЗ при случайных фазовых искажениях вихревого лазерного пучка. Для измерения TЗ мы используем цилиндрическую линзу [12]. Гауссов пучок с диаметром перетяжки w = 1,1 мм освещает пространственный модулятор света (SLM), на котором записана вихревая фаза mϕ с m =5. Каждый пиксель SLM искажается добавлением числа 2πα к его фазе mϕ. Величина α является случайным числом в интервале [0, 1]. На рис. 5

показаны искажённые фазы начального светового поля, записанные на SLM (левый столбец), распределения интенсивности (600 × 600 мкм), измеренные в фокальной плоскости сферической линзы с фокусным расстоянием f = 150 мм (центральный столбец), и распределения интенсивности (1900 × 1900 мкм), измеренные на двойном фокусном расстоянии от цилиндрической линзы с фокусным расстоянием f = 100 мм (правый столбец) для разных фазовых искажений α .

а)

б)

в)

г)

д)

е)

Рис. 4. Распределения интенсивности (a, в, д) и фазы (б, г, е) Гауссова пучка с начальным дробным ТЗ μ = 3,3 в ближней зоне (a, б), в зоне Френеля (в, г) и в дальней зоне (д, е). Стрелками на распределениях фазы показаны оптические вихри плюс первого порядка, а пунктирной стрелкой (е) показан оптический вихрь минус первого порядка. Для фазы чёрный цвет – это ноль, а белый цвет – 2π

б)

з)

о)

в)

г)

д)

е)

Уж1 Е2Я

I ™ Я шшЖ

и)       к) Ж'1ы

и)

к)

^

л)

II

м)

п)

р)

с)

т)

Рис. 5. Искажённые фазы (a, г, ж, к, н, p), распределения интенсивности (600 × 600 мкм) в фокальной плоскости сферической линзы с фокусным расстоянием f = 150 мм (б, д, з , л, о, с) и распределения интенсивности (1900 × 1900 мкм) на двойном фокусном расстоянии от цилиндрической линзы с фокусным расстоянием f = 100 мм (в, е, и, м, п, т) для разной степени искажения: α = 0 (а, б, в), α = 0,2 (г, д, е), α = 0,4 (ж, з, и), α = 0,6 (к, л, м), α = 0,8 (н, о, п), α = 1,0 (р, с, т)

Согласно рис. 5 при α =0,6 (то есть фаза искажается случайным значением в интервале [0; 1,2 π ]) всё ещё чётко видны 6 пиков на диагонали под углом –45° (или 5 тёмных полос, или 5 нулей интенсивности), что означает, что TЗ оптических вихрей равен 5. Однако при α ≥ 0,8 TЗ не может быть обнаружен (рис. 5). То есть ТЗ оптического вихря остаётся целым числом, равным 5, вплоть до величины случайного искажения начальной фазы ОВ, примерно равной половине длины волны ( λ /2).

Заключение

В работе теоретически показано, что Гауссов пучок, в который внедрён оптический вихрь с начальным дробным ТЗ, при распространении не сохраняет начальный ТЗ. Топологический заряд Гауссова пучка с начальным дробным ТЗ в разных зонах дифракции («ближней зоне» (z << z0), зоне Френеля (z ≈ z0) и дальней зоне (z >> z0)) может быть разный. Это подтверждено численным моделированием с помощью программы BeamProp (в ближней зоне и зоне дифракции Френеля) и с помощью преобразования Фурье (в дальней зоне). Описаны 4 типа эволюции Гауссова пучка с начальным дробным ТЗ. Один из них, например, такой. Если в начальной плоскости ТЗ равен 3,3, то в «ближней зоне» ТЗ равен 3, в зоне Френеля 4, а в зоне Фраунгофера (в фокусе сферической линзы) опять 3. Таким образом, в этом типе эволюции в зоне Френеля появляется ТЗ +1, а затем в дальней зоне появляется ещё ТЗ –1, который компен- сирует ТЗ +1. Но «рождаться» в ходе распространения дополнительные ОВ могут не только в случае начального дробного заряда, но и в случае комбинированного пучка, состоящего из линейной комбинации двух мод Лагерра–Гаусса с номерами (0, n) и (0, m) и разными радиусами перетяжек Гауссовых пучков. В этом случае могут «рождаться» сразу несколько ОВ |n – m|. Уничтожение ОВ происходит в том смысле, что «рождаются» ещё |n – m| ОВ, но с обратными по знаку ТЗ. Экспериментально показано, что при слабых случайных фазовых искажениях ОВ (величина задержки фазы меньше π) ТЗ сохраняется. Поэтому для идентификации ОВ в системах беспроводной связи можно использовать измерение ТЗ (наряду с измерением ОУМ).

У читателя может возникнуть вопрос: откуда берутся дополнительные ОВ в зоне Френеля и Фраунгофера (см. табл. 1)? Ответ может быть таким. Начальное световое поле с дробным ТЗ содержит весь спектр угловых гармоник и «несёт» в себе эти дополнительные ОВ. Доказательством могут служить два хорошо известных случая. Если в начальной плоскости имеется пучок Эрмита–Гаусса с номером (0, n ), прошедший через цилиндрическую линзу, повернутую в начальной плоскости на угол в 45° к декартовым осям, то ТЗ такого пучка в начальной плоскости равен нулю. Но на расстоянии, равном двойному фокусному расстоянию цилиндрической линзы, формируется вихревой пучок Лагерра–Гаусса (ЛГ) с номером (0, n ) [16]. Это означает, что «родился» оптический вихрь с ТЗ n. Другой пример. Пусть в начальной плоскости имеется суперпозиция Гауссова пучка с радиусом перетяжки w 1 и оптический вихрь ЛГ с номером (0, n ) и радиусом перетяжки w 2 . И пусть w 1 (0) <  w 2 (0), тогда [4] в начальной плоскости и далее до расстояния z 1 ТЗ такого комбинированного пучка будет равен n . Но при z >  z 1 , когда w 1 ( z ) >  w 2 ( z ), ТЗ пучка изменится и станет равен нулю. Это означает, что «родились» n оптических вихрей с ТЗ –1, которые «скомпенсировали» n оптических вихрей с ТЗ +1, которые были в начальной плоскости.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 1829-20003 , теоретические результаты, и грант № 1807-01129 , результаты моделирования), Российского научного фонда (грант № 18-19-00595 , эксперимент), а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (введение и заключение).