R/s анализ временных рядов излучения импульсного электроионизационного СО-лазера

Отличительной особенностью электроио-низационного СО-лазера (СО-ЭИЛ) являются его высокие выходные энергетические характеристики и богатый спектр излучения. Вместе с тем СО-ЭИЛ – сложная для анализа система, отличающаяся многообразием взаимосвязанных процессов, которые определяют динамику его излучения. Среди созданных к настоящему времени газовых лазеров, элект-роионизационные СО-лазеры (СО-ЭИЛ) обладают наибольшими КПД генерации ( ~ 3545%) и удельными энергосъемами (до 150 -200 Дж/л-Амага). До настоящего времени исследование СО-ЭИЛ проводилось либо экспериментально, либо путем численного расчета при использовании существующей модели. Однако наличие в этой модели большого количества взаимозависимых параметров молекулы СО делают такой расчет достаточно приближенным. В данной работе предлагается использовать метод R/S - анализа, позволяю- щий объединить два этих подхода.

Эмпирический закон Херста

Свой эмпирический закон гидрогеолог Харольд Эдвин Хёрст открыл, занимаясь изучением особенностей водного баланса Нила. Впоследствии оказалось, что многие другие природные явления хорошо описываются этим законом [1].

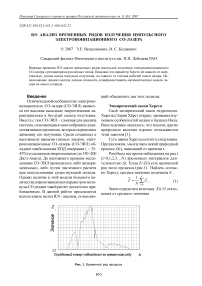
Суть закона Херста состоит в следующем. Предположим, мы изучаем некий природный процесс Z(t), зависящий от времени t.

Разобьем все время наблюдения на ряд i (i=0,1,2,3…N) временных интервалов длительностью A t. Тогда Z=Z(i) есть временной ряд этого процесса (рис.1). Найдем, согласно Херсту, среднее значение величины Z .

1 ^N

Z = «2 Z .          (1)

N i = 0

Затем определим величину X(i,N) отклонения от среднего значения

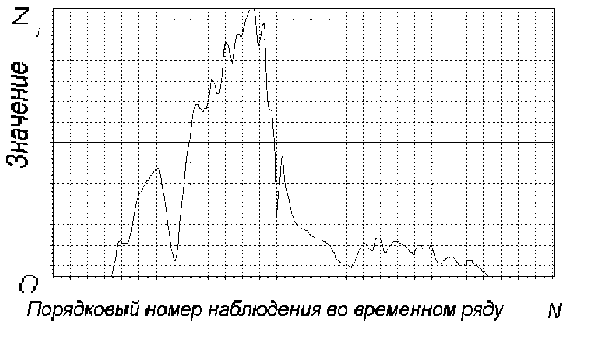
Рис. 1. Временной ряд процесса

X (i, N ) = £ Z . — Z ) .         ₍2)

j = 0

Далее определим величину R, которая носит название максимального размаха ис- следуемого ряда

R = max X (—

I I N ))

—

min X f—

I I N ))

и среднее квадратичное отклонение наблюдений

s

.

N

Как показал Херст, для многих природных явлений справедливо следующее равенство

R = N H S

,

где величина H , впоследствии названная показателем Херста, может меняться от 0 до 1. Показатель Херста, определяемый как

H = z ' lg ( N )

где R – максимальный размах исследуемого ряда; S – СКО наблюдений; n – количество наблюдений, служит удобной мерой устой- чивости статистического явления.

Показатель Хёрста

Если показатель Херста принимает значения 0 < H < 1, но не равен 0,5, то ряд является фракталом, поведение которого существенно отличается от случайных блужданий при Н = 0,5 [2].

Для процесса с Н > 0.5 тенденция к увеличению в прошлом означает тенденцию к увеличению в будущем. И наоборот, тенденция к уменьшению в прошлом означает, в среднем, продолжение уменьшения в будущем. Такой процесс называется персистентным.

При Н=0.5 никакой выраженной тенденции процесса не проявляется, и нет оснований считать, что она появится в будущем.

Случай Н < 0.5 характеризуется антиперсистентностью – рост в прошлом означает уменьшение в будущем, а тенденция к уменьшению в прошлом делает вероятным увеличение в будущем.

Этот подход и был использован при исследовании временных рядов излучения импульсного электроионизационного СО-лазера.

Методика эксперимента

Экспериментальные исследования излучения импульсного электроионизацион-ного СО-лазера проводились на установке, основой которой являлся охлаждаемый до криогенных температур импульсный СО-ЭИЛ-С лазер[4] . В экспериментах использовался либо неселективный резонатор лазера, либо селективный резонатор, одним из элементов которого была отражательная дифракционная решетка ( ДР₂ , t=0.01мм, угол блеска α ₀ = 30⁰) (рис. 2 (а-г)). В ходе работы измерялись спектрально-временные и энергетические характеристики излучения СО-ЭИЛ. Спектрограф для измерений строился по известной схеме Эберта [5].

Излучение лазера, проходя через плоскопараллельные пластины П₁ и П₂ из CaF₂ и последовательно отражаясь от сферических зеркал З₃ (R=2000 мм) и З₄ (R=3000 мм), образующих вместе со щелью Д₁ коллиматор, падало на дифракционную решетку ДР 1 (t=0,01MM, угол блеска a 0 = 30 0 ), образуя угол =24,29⁰ с нормалью к плоскости решетки. Дифрагированные лучи с помощью зеркала З₅ (R=3000 мм), фокусировались на экран Э₁, где для измерения абсолютного значения энергии излучения на отдельных колебательно-вращательных переходах молекулы СО или регистрации формы импульса излучения устанавливались либо калориметр К ₁ , либо охлаждаемый жидким азотом фоторезистор ФР₁ на основе Нe:Au (временное разрешение ~10^-7 сек). Часть энергии излучения, отраженная от граней пластины П ₁ и сфокусированная линзой Л₁ на калориметр К₂ (аналогичный калориметру К₁), позволяла судить о полной энергии излучения электроиони-зационного СО-лазера. Форма импульса излучения СО-ЭИЛ регистрировалась фоторезистором ФР₂ (аналогичным ФР₁).

Юстировка оптических элементов схемы и зеркал резонатора лазера осуществлялась с помощью гелий-неонового лазера He-NeI, излучение которого пластиной П2 заводилось в спектральную часть схемы, а последовательным отражением от плоскости П2 и П4 направлялось в резонатор лазера[6].

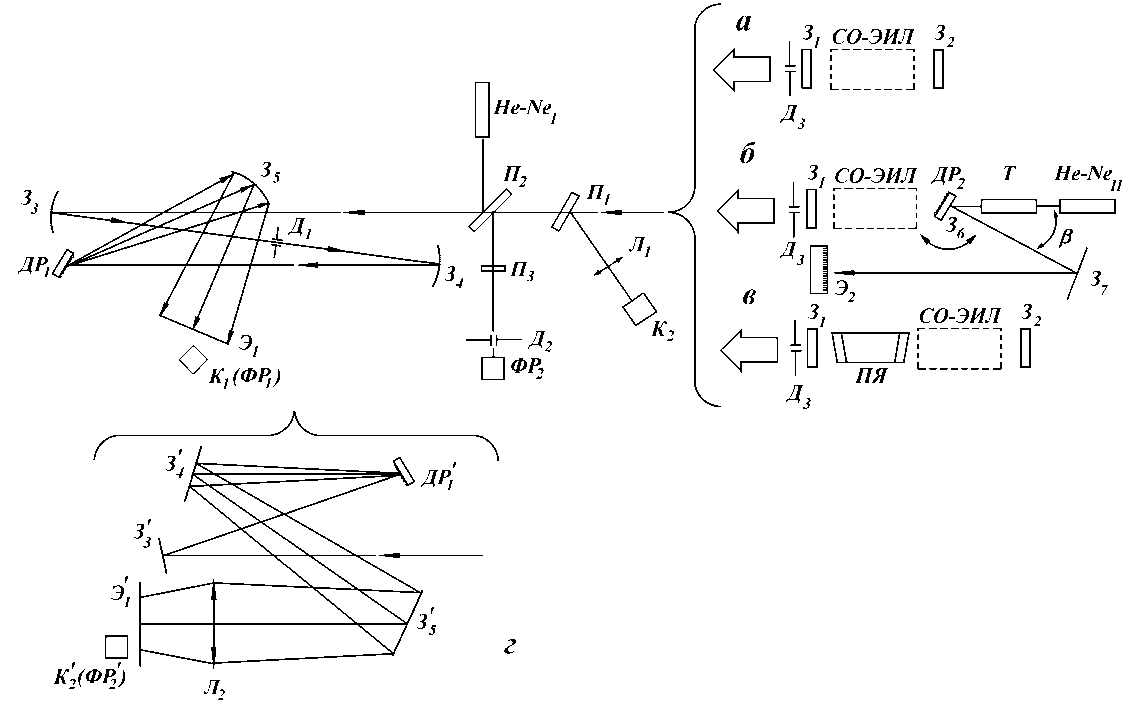
Рис. 2. Принципиальная схема измерения спектрально-временных характеристик излучения импульсного СО-ЭИЛ:

а – СО-ЭИЛ с неселективным резонатором; б – СО-ЭИЛ с селективным резонатором (дифракционная решетка);

в – СО-ЭИЛ с селективным резонатором (поглощающая водяная ячейка); г – спектральная схема с разрешением ~ 4см-1

Результаты и анализ полученных данных

В результате выполнения экспериментов были получены временные характеристики излучения импульсного СО-ЭИЛ для разных газовых смесей и с резонаторами различных типов.

Ряд осциллограмм импульсов излучения представлен на рис. 3.

Для получения временных рядов излучения проводилась оцифровка осциллограмм с помощью программы Graph Digitizer 1.8. Определение показателя Хер-

	Селективный резонатор, Qвкл=490Дж/л х Амага 12 ^ 11(Р14) λ =1800,43см-1		Селективный резонатор, Qвкл=490Дж/л х Амага 14 ^ 13(Р14) λ =1750,23см-1
	Селективный резонатор, Qвкл=500Дж/л х Амага 12 ^ 11(Р19) λ =1780,3см-1	11 j/i i KL L*h tn—-Ш	Неселективный резонатор, Qвкл=410Дж/л х Амага 10 ^ 9(Р10) λ =1870,7см-1

Рис. 3. Форма импульсов излучения СО-ЭИЛ для резонаторов различных типов для смеси СО: N2 - 1:9, N=0,5 Амага, развертка 25мкс/дел

Неселективный резонатор, рвкл.=410Дж/л: Амата 10->9(Р10) Х=1870.7см-1

Н=0.8958

Селективный резонатор, Qbkh . 490Дж/лх Амата 14->13(Р14) Х=1750.23см-1

Н=0.8466

Рис. 4. R/S анализ временных рядов мощности излучения СО-ЭИЛ с резонаторами различных типов для смеси СО:N2-1:9, N=0.5 Амага

ста осуществлялось на основе анализа временных рядов с использованием программы FRACTAN. Результаты R/S анализа временных рядов мощности излучения СО-ЭИЛ с резонаторами различных типов для смеси СО:N2-1:9, N=0.5 Амага представлены на рис. 4

Как показали эксперименты, для гелийсодержащих и безгелиевых смесей показатель Херста практически не зависит ни от длины волны импульса излучения, ни от величины энерговклада

Для смеси СО:N2 =1:9 показатель Херста оказался в среднем равен H=0,8679, а для смеси CO:N2 :He =1:9:10 эта величина составила H=0,8367. Таким образом, по- казатель Херста является своего рода “визитной карточкой” смеси определенного состава. Поскольку величина H для обеих смесей лежит в диапазоне 0.5<Н<1, это означает, что временные ряды импульсов излучения СО-ЭИЛ персистентны. Однако, из этого следует также и то, что среди большого ряда процессов, происходящих в колебательно-возбужденной системе молекул окиси углерода, есть некая причина, вносящая элемент хаоса, проявляющийся в особенностях временных характеристик излучения лазера. Этот важный момент обязательно должен присутствовать в теоретической модели, которая претендует на то, что она правильно описывает работу

8 -

А

С ^^ 0

6 -

4 -

2 -

9 760

Д.767Х103,                                                        В                                                         Д.942x103

Рис. 5. Сравнение поведения показателя Херста при разных энерговкладах (селективный резонатор):

А – показатель Н для 526,00 Дж; С – показатель Н для 578,34 Дж; В – длина волны в обратных см импульсного СО-ЭИЛ. В этом случае критерием правильности модели лазера, может служить тот факт, что величина показателя Херста временных рядов излучения импульсного СО-ЭИЛ, рассчитанных теоретически, соответствует показателю, полученному на основании экспериментальных данных.

Выводы

• 1.    Впервые проведен R/S анализ временных рядов излучения импульсного СО-ЭИЛ с резонаторами различных типов.

• 2.    Показано, что для СО-ЭИЛ с составом рабочей смеси СО:N₂ =1:9 показатель Херста в среднем равен H =0,8679. Для смеси CO :N₂ :Нe=1:9:10 эта величина равна H =0,8367.

• 3.    Для гелийсодержащих и безгелиевых смесей показатель Херста временных рядов излучения СО-ЭИЛ практически не зависит ни от длины волны импульса излучения, ни от величины энерговклада.

• 4.    Показатель Херста является характеристикой, использование которой может позволить проверить существующие теоретические модели этого лазера на адекватность описания процессов, протекающих в активной среде СО-ЭИЛ.