Самоконфигурируемый ансамбль генетических алгоритмов для решения задач мультимодальной оптимизации
Автор: Сопов Е.А., Аплеснин С.С.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 т.16, 2015 года.
Бесплатный доступ
Задача мультимодальной оптимизации (ММО) заключается в нахождении множества всех глобальных и локальных оптимумов или аппроксимации этого множества. В последние годы было предложено множество эффективных бионических и эволюционных алгоритмов для ММО с вещественными переменными (в частности, на базе алгоритмов эволюционных стратегий, роя частиц (PSO), дифференциальной эволюции и др.). В то же время, многие практические задачи оптимизации часто содержат переменные нескольких разных типов, включая целочисленные, ранговые, бинарные и др. В таком случае переменные переводятся в наиболее слабую из шкал, обычно используется бинарное представление решений. К сожалению, сегодня достаточно эффективных подходов для ММО с бинарным представлением не предложено. Существующие решения в основном базируются на общих идеях метода ниш (niching). Более того, возникает проблема выбора подходящего алгоритма и тонкой настройки его параметров под конкретную задачу ММО. Предложен новый подход, основанный на метаэвристике для построения генетического алгоритма, включающего многие стратегии поиска. Предложенный подход позволяет управлять взаимодействием нескольких поисковых алгоритмов (разных генетических алгоритмов для ММО) и обеспечивает самоконфигурируемое решение задачи с априори неизвестной структурой (оптимизация «черного ящика»). Представлены результаты численных экспериментов и сравнение с другими известными подходами на множестве традиционных тестовых задач ММО и задачах, предложенных на конкурсе по ММО в рамках конференции CEC’2013. Предложенный подход демонстрирует эффективность лучшую, чем стандартные подходы, основанные на идее ниш, и сравнимую с современными усовершенствованными алгоритмами. Особенностью и преимуществом предложенного подхода является то, что он не требует привлечения дополнительных экспертных знаний, так как работает в автоматизированном, самоконфигурируемом режиме.
Мультимодальная оптимизация, самоконфигурирование, генетический алгоритм, метаэвристика, метод ниш
Короткий адрес: https://sciup.org/148177501
IDR: 148177501 | УДК: 519.85
Текст научной статьи Самоконфигурируемый ансамбль генетических алгоритмов для решения задач мультимодальной оптимизации
Введение. Многие прикладные задачи оптимизации имеют более одного оптимального решения, или существует один глобальный оптимум и множество локальных оптимумов в допустимой области пространства поиска. Такие задачи оптимизации называются многоэкстремальными или мультимодальными. Цель задачи мультимодальной оптимизации (ММО) -найти множество всех глобальных и локальных оптимумов или репрезентативную аппроксимацию этого множества.
Эволюционные алгоритмы (ЭА) в целом и генетические алгоритмы (ГА) в частности демонстрируют высокую эффективность для многих сложных задач оптимизации. ЭА и ГА эффективны и при решении многоэкстремальных задач, так как используют стохастический популяционный поиск вместо последовательного улучшения единственного решения. В то же время традиционные ЭА и ГА имеют тенденцию сходиться к лучшему найденному решению и теряют разнообразие популяции.
В последние годы задача ММО становится более полярной, было предложено множество эффективных бионических и эволюционных подходов для ММО. Практически все алгоритмы построены на идее поддержки разнообразия популяции, но отличаются способами исследования пространства поиска, обнаружения и идентификации областей притяжения оптимумов. На сегодняшний день большинство алгоритмов и наилучшие результаты получены для задач ММО с вещественными переменными [1]. Основная причина - лучшее понимание и использование свойств ландшафта целевой функции в вещественном пространстве поиска. В итоге, было разработано множество хорошо обоснованных эвристик.
К сожалению, многие практические задачи ММО обычно являются задачами типа «черного ящика», что затрудняет применение алгоритмов ММО. Более того, многие практические задачи оптимизации часто содержат переменные нескольких разных типов, включая целочисленные, ранговые, бинарные и др. В таком случае переменные переводятся в наиболее слабую из шкал, обычно используется бинарное представление решений. К сожалению, сегодня достаточно эффективных подходов для ММО с бинарным представлением не предложено. Существующие решения в основном базируются на общих идеях метода ниш (niching) и разделения пригодности (fitness sharing). Эвристики из эффективных алгоритмов для ММО с вещественным представлением решений не могут быть напрямую применены для задач с бинарным представлением из-за разности свойств вещественного и бинарного пространств поиска.
В данной работе предложен новый подход, основанный на метаэвристике для построения генетического алгоритма, включающего многие стратегии поиска. Основная идея - создать ансамбль из нескольких ММО-алгоритмов и адаптивно управлять их взаимодействием. Такой подход обеспечит самокон-фигурируемое решение задач ММО с априори неизвестной структурой.
Состояние исследований в области ММО. Задача идентификации многих экстремумов существует с момента появления ЭА. В ранних работах особенности ММО учитывались для усиления стандартных ЭА и ГА при нахождении глобального оптимума в мультимодальной среде.
Сегодня задача ММО имеет как минимум 3 постановки [2]:
-
- поиск единственного (глобального) оптимума многоэкстремальной задачи;
-
- поиск всех глобальных оптимумов;
-
- поиск всех оптимумов (глобальных и локальных) или их репрезентативного подмножества.
Очевидно, что 2 и 3 постановки более интересны как с теоретической, так и практической точек зрения. Интерес к ММО в последнее десятилетие существенно повысился. Последние достижения в этой области в основном сфокусированы на задаче поиска многих оптимумов задачи, предложено большое количество различных эффективных эвристик. В 2013 году состоялся глобальный конкурс по ММО в рамках Международной конференции IEEE CEC’13 [3], где были сформулированы тестовые задачи, требования для сравнения эффективности алгоритмов ММО и представлены современные подходы к решению сложных задач ММО.
Список наиболее популярных и хорошо исследованных подходов включает [1; 4; 5]:
-
1) базовые эвристики:
-
- параллельный и последовательный метод ниш (niching);
-
- разделение пригодности (fitness sharing), метод «очистки» популяции (clearing) и метод ниш, основанный на кластеризации (duster-based niching);
-
- контроль скопления (crowding);
-
- турнирная селекция с ограничением (restricted tournament selection (RTS));
-
- ограничение спаривания (mating restriction);
-
- сохранение особей (species conservation);
-
2) специальные подходы:
-
- метод ниш с локальным поиском (niching memetic algorithm);
-
- многонациональная модель ЭА (multinational EA);
-
- двухкритериальный ЭА для ММО (bi-objective MMO EA);
-
- ЭА для ММО с использованием кластеризации (clustering-based MMO EA);
-
- популяционный метод ниш (population-based niching);
-
- топологические алгоритмы (topological algorithms);
-
3) другие бионические алгоритмы, модифицированные для решения задач ММО: метод роя частиц
(PSO), эволюционные стратегии (ES), дифференциальная эволюция (DE), алгоритм муравьиной колонии (ant colony optimization) и др.
Примечание . Далее в статье будут использоваться оригинальные названия подходов и алгоритмов и их специфичных параметров на английском языке, так как не все названия имеют компактный перевод, сохраняющий исходный смысл, а общепринятой терминологии на русском языке пока нет.
Бинарные и бинаризованные задачи ММО обычно решаются с помощью ГА, использующих базовые эвристики. Некоторые специальные подходы применяются, но часто их свойства в бинарном пространстве поиска теряются. К сожалению, многие эффективные бионические алгоритмы для ММО не имеют бинарной модификации и не могут быть без потерь преобразованы для задач с бинарным представлением решений.
Исследования в области ММО показывают, что на текущий момент не предложено универсального подхода, который бы эффективно справлялся с произвольными (или хотя бы многими) задачами ММО. Многие исследователи предпочитают разрабатывать гибридные схемы, которые объединяют поисковые алгоритмы и различные эвристики для улучшения метода ниш. В качестве примера можно привести 4 алгоритма-победителя с конкурса по ММО CEC’13:
-
- Niching the CMA-ES via Nearest-Better Clustering (NEA2);
-
- A Dynamic Archive Niching Differential Evolution algorithm (dADE/nrand/1;
-
- CMA-ES with simple archive (CMA-ES);
-
- Niching Variable Mesh Optimization algorithm (N-VMO) [6].
Другой подход - комбинация многих ММО-алгоритмов, которые решают задачу параллельно, обмениваются индивидами и обобщают результаты. В [7] применяется островная модель, в которой острова итеративно переопределяются в зависимости от генетической близости индивидов. В [8] четыре алгоритма на базе метода ниш работают параллельно и производят потомков, которые собираются в общий пул для реализации шага замещения. В [9] аналогичная схема реализована с алгоритмом «очистки».
Концепция проектирования алгоритма ММО в виде ансамбля является весьма перспективной. Метаэвристика, которая включает различные подходы для ММО (различные стратегии поиска), должна справляться с различными типами задач ММО. Такая метаэвристика может быть самоконфигурируемой за счет адаптивного управления взаимодействием алгоритмов в процессе работы.
В [10] был предложен самоконфигурируемый генетический алгоритм на базе многих стратегий поиска, являющийся гибридом островной модели конкурирующей и кооперационной коэволюции. Подход основан на параллельной и независимой работе многих различных ГА, реализующих различные стратегии поиска. Такой подход позволяет решать задачи оптимизации с различными свойствами (в рамках определенного класса задач). Подход продемонстрировал хорошие результаты для задач многокритериальной и нестационарной оптимизации.
Самоконфигурируемый ансамбль ГА ММО. В области прикладной статистики и машинного обучения часто используется метод ансамблей алгоритмов для повышения надежности принятия решений. В среднем коллективное решение из частных решений многих алгоритмов дает лучшие результаты, чем полученные от них по отдельности. Эту концепцию можно применить и для бионических алгоритмов, и, в частности, для ГА. Основная идея - включить в ансамбль разные стратегии поиска и организовать эффективное управление их взаимодействием. Основная гипотеза - различные ГА учитывают различные особенности задач оптимизации и предназначены для преодоления различных трудностей в ходе работы. Вероятность того, что все ГА не справятся с некоторой ситуацией во время решения задачи, крайне низка. Более того, взаимодействие алгоритмов может обеспечить ансамбль новыми свойствами, которые отсутствуют у частных алгоритмов (синергетический эффект).
Структура самоконфигурируемого ГА на базе многих стратегий поиска, предложенного в [10], представлена на рис. 1. Общая схема метаэвристики обозначается как Self*GA, где символ звезды заменяется на ссылку на конкретный класс задач оптимизации при формировании коллектива ГА.
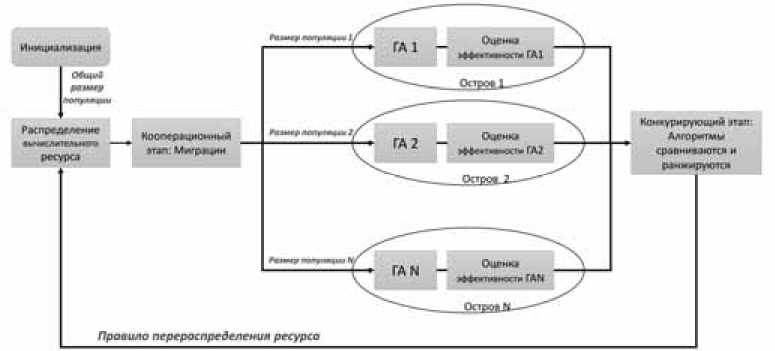
Рис. 1. Общая схема Self*GA
Общий размер популяции называется вычислительным ресурсом. Ресурс распределяется между алгоритмами, которые работают параллельно и независимо в течение определенного числа поколений (которое называется «период адаптации»). После распределения ресурсов каждый ГА в составе ансамбля имеет свою собственную популяцию, не пересекающуюся с популяциями других ГА. При инициализации все алгоритмы получают равные порции вычислительного ресурса. Эта концепция соответствует островной модели ГА, где каждый остров реализует свою собственную стратегию поиска.
По окончании адаптационного периода оцениваются показатели эффективности частных алгоритмов, алгоритмы ранжируются. ГА, показавшие более высокую эффективность, увеличивают свой вычислительный ресурс (размеры своих популяций) за счет менее эффективных алгоритмов. В то же время все алгоритмы имеют определенное количество ресурса, которое не перераспределяется, чтобы дать шанс менее эффективным алгоритмам проявить себя в будущем в других ситуациях. Эта концепция соответствует конкурирующей коэволюции.
Далее выполняются случайные миграции индивидов, чтобы уравнять стартовые позиции алгоритмов на следующий период адаптации. В зависимости от оптимизационной задачи, такие миграции могут быть детерминированные, основанные на операторе селекции или случайные. Эта концепция соответствует кооперативной коэволюции.
Данный подход позволяет избавиться от необходимости выбора подходящей стратегии поиска под конкретную задачу оптимизации, так как выбор лучших алгоритмов происходит автоматически в процессе поиска.
Аналогично можно построить ансамбль для задач ММО. Такой алгоритм может быть назван SelfMMOGA (MMO - multimodal optimization). На первом этапе определяются индивидуальные алгоритмы, включенные в состав ансамбля. В данной работе используются шесть базовых подходов, которые хорошо исследованы [1; 11] и могут применяться для задач с бинарным представлением. Мотивация такого выбора: если SelfMMOGA эффективен с ансамблем базовых алгоритмов, то в будущем алгоритм можно усилить более совершенными подходами.
Алгоритмы и их специфичные параметры представлены в табл. 1. Для значений параметров радиусов и расстояний используется метрика Хемминга для задач с бинарным представлением и евклидова метрика - для вещественных переменных.
Период адаптации является настраиваемым параметром алгоритма, его значение зависит от ограничений на вычислительный ресурс (число вычислений функции пригодности).
Важным моментом в любой коэволюционной схеме является способ оценки эффективности отдельных алгоритмов. Для задач ММО критерии должны включать оценку количества найденных оптимумов и то, как популяция распределена в пространстве поиска. К сожалению, хорошие метрики предложены только для тестовых задач ММО, в которых число оптимумов и их характеристики известны. Способы оценки эффективности для задач ММО, являющихся моделью «черного ящика», до сих пор обсуждаются. Некоторые рекомендации можно найти в [12]. В этой работе используются следующие критерии.
Первая метрика - BR (Basin Ratio) определяет число идентифицированных областей притяжения оптимумов, которые найдены общей популяцией (всеми индивидами всех алгоритмов). Метрика не требует предварительных знаний об оптимумах задачи, так как строится их аппроксимация в процессе работы. BR вычисляется следующим образом:
BR( pop) =1,(1)
k kI l = £ min 11, £ b(x, z,) >, i=1 I xe pop
I x *
11,if x e basin(z) b (x,z) = 1 л ■,
| 0, otherwise где pop - популяция оцениваемого ГА; k - число идентифицированных областей притяжения; l - индикатор покрытия области притяжения алгоритмом; b - функция, определяющая попадание индивида в область притяжения оптимума.
Для использования метрики (1) необходимо выбрать способ идентификации областей притяжения оптимумов и определить функцию b ( x , z ).
Таблица 1
Алгоритмы в составе SelfMMOGA и их параметры
|
Обозначение |
Алгоритм |
Параметры |
|
Alg1 |
Clearing |
Clearing radius, Capacity of a niche |
|
Alg2 |
Sharing |
Niche radius, a |
|
Alg3 |
Clustering |
Number of clusters, min distance to centroid, max distance to centroid |
|
Alg4 |
Restricted Tournament Selection (RTS) |
Window size |
|
Alg5 |
Deterministic Crowding |
— |
|
Alg6 |
Probabilistic Crowding |
— |
Для вещественных задач ММО области притяжения могут быть определены с помощью различных процедур кластеризации, например, алгоритмов Джависа-Патрика, ближайшего-лучшего и др. [13]. В данной работе для задач ММО с бинарным представлением используется следующий подход. Используется общая популяция (объединение популяций всех алгоритмов SelfMMOGA). Для каждого индивида рассматривается предопределенное количество 5 его ближайших соседей (в метрике Хемминга). Если пригодность выбранного индивида лучше, он помечается как локальный оптимум и центр идентифицированной области притяжения. Число ближайших соседей является настраиваемым параметром. Для прикладных задач значение может выбираться из практических соображений. Псевдокод процедуры имеет следующий вид:
Z = 0 ;
for all (x е общая популяция) { for i=1,..,S yi=ближайший сосед(x);
if ( fitness(x) > fitness(y i ) ) for all y i {
Z = Z + x;
};
}; _______________________________________________________
Функция b ( x , z ) определяет, находится ли индивид x в предопределенном радиусе относительно центра области притяжения z . Радиус является настраиваемым параметром. В данной работе радиус определяется как
.. total population size radius =------------------- (2)
где k - число идентифицированных областей притяжения ( k = |Z |).
Вторая метрика - SDNN (Sum of Distances to Nearest Neighbour) определяется как сумма расстояний до ближайших соседей. Этот критерий не требует информации об оптимумах и областях притяжения и используется как штраф за потерю разнообразия (кластеризацию решений). Метрика SDNN может быть вычислена следующим образом:
popsize
SDNN( pop ) = £ d nn ( x , ., pop ), (3)
i = 1
d nn ( x , , pop ) = min { dist ( x , y ) } ,
-
У е pop \{ x }
где dnn - расстояние до ближайшего соседа; dist - метрика Хемминга.
Метрики BR и SDNN объединяются в интегральный критерий K :
K = «• BR ( pop ) + (1 -а ) • SDNN( pop ), (4)
где SDNN - нормализованное значение SDNN; а определяет вес частных критериев в сумме (а е [0,1]).
Далее необходимо определить схему перераспределения вычислительного ресурса: определяются размеры популяций каждого ГА на следующий период адаптации. В данной работе все алгоритмы отдают алгоритму-победителю заданный процент размера своих популяций с учетом минимально гарантированного значения ресурса, который не распределяется.
На кооперационной стадии во многих коэволюци-онных алгоритмах применяется схема, когда новый период адаптации начинается с одинаковых стартовых точек по принципу «лучшие вытесняют худших». Для задач ММО лучшие решения определяются идентифицированными локальными оптимумами. Поскольку аппроксимация множества оптимумов уже выполнена на предыдущих шагах (множество Z ), индивиды из Z копируются в популяции частных алгоритмов, замещая наиболее близких к ним индивидов.
Критерии останова в SelfMMOGA такие же, как в стандартном ГА: ограничение на число вычислений целевой функции, число поколений без улучшений, стагнация и т. д.
Результаты численных экспериментов. Для оценки предложенного подхода использовались следующие наборы тестовых задач:
-
1. Шесть бинарных задач ММО, предложенных в [8]. Данные задачи основаны на функции подсчета единиц (the unitation functions) и являются существенно мультимодальными и десептивными.
-
2. Восемь вещественных задач ММО, предложенных на конкурсе по ММО в рамках международной конференции IEEE CEC’13 [6].
В табл. 2 представлены обозначения и некоторые детали тестовых задач.
Таблица 2
Набор тестовых задач
|
Обозначение задачи |
Число оптимумов |
Размерность задачи* |
|
binaryF11 |
32 global |
30 |
|
binaryF12 |
32 global |
30 |
|
binaryF13 |
27 global |
24 |
|
binaryF14 |
32 global |
30 |
|
binaryF15 |
32 global |
30 |
|
binaryF16 |
32 global |
30 |
|
cecF1 |
2 global + 3 local |
9, 12, 15, 19, 22 |
|
cecF2 |
5 global |
4, 7, 10, 14 ,17 |
|
cecF3 |
1 global + 4 local |
4, 7, 10, 14 ,17 |
|
cecF4 |
4 global |
14, 22, 28, 34, 42 |
|
cecF5 |
2 global + 2 local |
11, 17, 24, 31, 37 |
|
cecF6 |
18 global + 742 local |
16, 22, 30, 36, 42 |
|
cecF7 |
36 global |
14, 20, 28, 34, 40 |
|
cecF8 |
12 global |
8, 14, 20, 28, 34 |
* Вещественные задачи предварительно были бинаризованы, используя стандартное бинарное кодирование с 5 уровнями точности.
Для оценки эффективности SelfMMOGA на тестовых задачах с вещественными переменными использованы следующие критерии:
-
- PR (Peak Ratio) - процент оптимумов, найденных алгоритмом (5);
-
- SR (Success Rate) - процент успешных запусков алгоритма, когда были найдены все оптимумы задачи:
{q е Q л dm (q,pop) <е}|
PR =------------------ k
где Q = { q 1 , q 2 ,..., qk } - множество всех известных оптимумов; е - уровень точности.
Максимальное число вычислений целевой функции и уровни точности для вычисления PR - в соответствии с правилами конкурса CEC [6]. Число независимых запусков алгоритма - 50.
В случае бинарных задач уровни точности для PR не могут быть определены, поэтому необходимо найти конкретную точку в пространстве поиска. Критерий SR был заменен метрикой PD (Peak Distance), которая показывает среднее расстояние от известного оптимума до ближайшего индивида в популяции [12]:
1 k
PD=тЕ d™ ( q - , pop ). (6) k i = 1
Для наглядного представления процесса управления взаимодействием ГА в SelfMMOGA был выбран и визуализирован произвольный запуск алгоритма на задаче cecF1. График изменения популяций (перераспределение ресурсов) показан на рис. 2. Общий размер популяции равен 200 индивидам, размер гарантированного ресурса - 10. Максимальное число поколений - 200, период адаптации - 10. Таким образом, на горизонтальной оси графика отмечено 20 периодов адаптации, на вертикальной - значение размера популяции каждого ГА.
Как мы видим, нет ни одного алгоритма, кто бы «выигрывал» все время. На первых двух периодах лучшую эффективность показали Alg2 (Sharing) и Alg1 (Clearing). Наибольшее количество ресурса получил Alg3 (Clustering) на 10-м периоде адаптации. На финальных этапах лучшие результаты показал Alg5 (Deterministic Crowding).
Результаты оценки эффективности SelfMMOGA на множестве задач с бинарным представлением представлены в табл. 3. Таблица содержит значения по метрикам PR, SR и PR, усредненным по 50 незави симым запускам алгоритма. Результаты сравнены с результатами реализации ансамбля различных алгоритмов на основе метода ниш (ENA), предложенного в [8]. Оба алгоритма имели равное ограничение на максимальное число вычислений целевой функции, для алгоритма ENA в первоисточнике представлены только значения по метрике SR.
Настройки SelfMMOGA следующие:
-
- максимальное число вычислений целевой функции - 50 000 (как и у ENA);
-
- размер общей популяции (сумма размеров популяций всех ГА) - 200 (ENA использует 500);
-
- период адаптации - 10 поколений 25 раз;
-
- все стандартные параметры ГА являются само-настраиваемыми - используется идея, предложенная в [14].
Результаты показывают, что бинарные проблемы оказались не таким сложными для SelfMMOGA и ENA. Для более детального анализа в табл. 4 результаты работы SelfMMOGA сравнены с результатами каждого из его частных алгоритмов, реализованных по отдельности. Также вычислено среднее значение (столбец «Mean») по показателям 6 частных алгоритмов. Оценку среднего можно рассматривать как среднюю эффективность при случайном выборе алгоритма (из представленных 6). Такая оценка весьма полезна, так как в случае задач ММО, являющихся «черным ящиком», исследователь не имеет информации о задаче и, как следствие, не может выбрать подходящий ГА. Если эффективность SelfMMOGA оказывается выше средней эффективности алгоритмов в его составе, то выбор SelfMMOGA будет предпочтительнее.
Как видно из табл. 4, SelfMMOGA на бинарных задачах во всех случаях превосходит среднее значение. Более того, в задачах F15 и F16 ни один из частных алгоритмов не достиг значения SR, равного 1, но их ансамбль в SelfMMOGA показал максимальную эффективность.
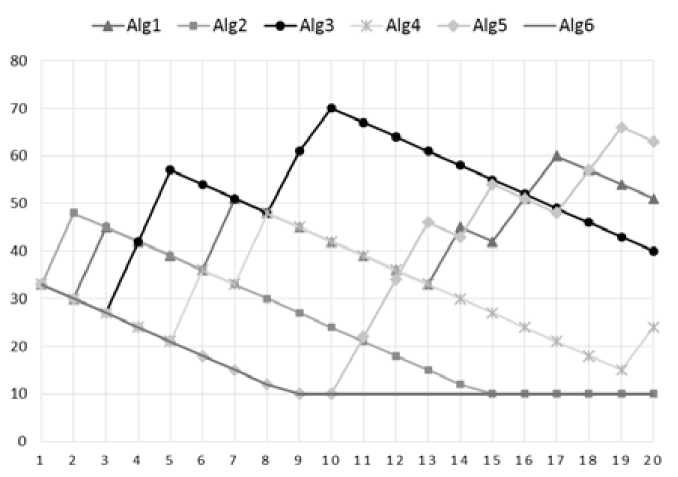
Рис. 2. Пример управления размером популяций в SelfMMOGA
Результаты экспериментов на наборе бинарных задач
Таблица 3
|
Задача |
SelfMMOGA |
ENA |
||
|
PR |
SR |
PD |
SR |
|
|
binaryF11 |
1,00 |
1,00 |
0,00 |
1,00 |
|
binaryF12 |
1,00 |
1,00 |
0,00 |
1,00 |
|
binaryF13 |
1,00 |
1,00 |
0,00 |
1,00 |
|
binaryF14 |
1,00 |
1,00 |
0,00 |
1,00 |
|
binaryF15 |
1,00 |
1,00 |
0,00 |
1,00 |
|
binaryF16 |
1,00 |
1,00 |
0,00 |
0,99 |
Детализированные результаты экспериментов на наборе бинарных задач
Таблица 4
|
Alg1 |
Alg2 |
Alg3 |
Alg4 |
Alg5 |
Alg6 |
Mean |
Self-MMOGA |
|
|
Задача: binaryF11 |
||||||||
|
PR |
0,94 |
0,84 |
0,91 |
1,00 |
0,97 |
0,78 |
0,91 |
1,00 |
|
SR |
0,90 |
0,84 |
0,88 |
1,00 |
0,94 |
0,80 |
0,89 |
1,00 |
|
PD |
2,40 |
3,37 |
2,40 |
0,00 |
2,33 |
3,30 |
2,30 |
0,00 |
|
Задача: binaryF12 |
||||||||
|
PR |
0,97 |
0,97 |
1,00 |
1,00 |
0,97 |
0,84 |
0,96 |
1,00 |
|
SR |
0,96 |
0,98 |
1,00 |
1,00 |
0,94 |
0,84 |
0,95 |
1,00 |
|
PD |
2,00 |
1,00 |
0,00 |
0,00 |
1,67 |
3,62 |
1,38 |
0,00 |
|
Задача: binaryF13 |
||||||||
|
PR |
1,00 |
0,96 |
0,96 |
0,93 |
0,96 |
0,89 |
0,95 |
1,00 |
|
SR |
1,00 |
0,96 |
0,94 |
0,90 |
0,94 |
0,84 |
0,93 |
1,00 |
|
PD |
0,00 |
2,50 |
2,67 |
2,80 |
2,67 |
3,37 |
2,34 |
0,00 |
|
Задача: binaryF14 |
||||||||
|
PR |
0,91 |
0,81 |
0,91 |
1,00 |
0,94 |
0,75 |
0,89 |
1,00 |
|
SR |
0,92 |
0,92 |
0,90 |
1,00 |
0,94 |
0,80 |
0,91 |
1,00 |
|
PD |
3,25 |
2,50 |
2,60 |
0,00 |
2,67 |
3,20 |
2,37 |
0,00 |
|
Задача: binaryF15 |
||||||||
|
PR |
0,88 |
0,88 |
0,84 |
0,88 |
0,88 |
0,72 |
0,84 |
1,00 |
|
SR |
0,88 |
0,86 |
0,84 |
0,86 |
0,84 |
0,64 |
0,82 |
1,00 |
|
PD |
2,33 |
2,57 |
2,62 |
2,71 |
2,37 |
3,06 |
2,61 |
0,00 |
|
Задача: binaryF16 |
||||||||
|
PR |
0,84 |
0,75 |
0,84 |
0,88 |
0,78 |
0,56 |
0,78 |
1,00 |
|
SR |
0,84 |
0,80 |
0,86 |
0,84 |
0,76 |
0,66 |
0,79 |
1,00 |
|
PD |
3,25 |
2,80 |
3,00 |
2,87 |
3,08 |
3,47 |
3,08 |
0,00 |
Результаты оценки эффективности SelfMMOGA на вещественных задачах представлены в табл. 5-7. Табл. 5 содержит детальную информацию, табл. 6 демонстрирует показатели в сравнении с другими известными алгоритмами, в табл. 7 сравниваемые алгоритмы проранжированы по критериям.
Все критичные настройки и ограничения алгоритмов при решении задач определены правилами конкурса CEC’13. Для каждой задачи используются 5 уровней точности для определения попадания в об ласть притяжения оптимума (е = {1e-01, 1e-02,..., 1e-05}). Таким образом, каждая задача была бинаризована 5 раз (размерности бинарного пространства поиска представлены в табл. 2).
Результаты работы SelfMMOGA сравнены с оценками эффективности других эффективных алгоритмов, представленных на конкурсе CEC’13: DE/nrand/1/bin and Crowding DE/rand/1/bin [6], N-VMO [15], dADE/nrand/1 [16] и PNA-NSGAII [17].
Таблица 5
Результаты экспериментов на наборе задач CEC’13
|
Уровень точности £ |
cecF1 |
cecF2 |
cecF3 |
cecF4 |
||||
|
PR |
SR |
PR |
SR |
PR |
SR |
PR |
SR |
|
|
1e-01 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
|
1e-02 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
|
1e-03 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
|
1e-04 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
|
1e-05 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
0,887 |
0,623 |
|
Уровень точности £ |
cecF5 |
cecF6 |
cecF7 |
cecF8 |
||||
|
PR |
SR |
PR |
SR |
PR |
SR |
PR |
SR |
|
|
1e-01 |
1,000 |
1,000 |
0,843 |
0,540 |
0,851 |
0,540 |
1,000 |
1,000 |
|
1e-02 |
1,000 |
1,000 |
0,834 |
0,536 |
0,792 |
0,223 |
1,000 |
1,000 |
|
1e-03 |
1,000 |
1,000 |
0,814 |
0,378 |
0,762 |
0,029 |
0,966 |
0,775 |
|
1e-04 |
1,000 |
1,000 |
0,560 |
0,140 |
0,731 |
0,000 |
0,964 |
0,753 |
|
1e-05 |
1,000 |
1,000 |
0,000 |
0,000 |
0,687 |
0,000 |
0,954 |
0,670 |
Таблица 6
Средние значения метрик
|
£ |
SelfMMOGA |
DE/nrand/1/bin |
cDE/rand/1/bin |
N-VMO |
dADE/nrand/1 |
PNA-NSGAII |
||||||
|
PR |
SR |
PR |
SR |
PR |
SR |
PR |
SR |
PR |
SR |
PR |
SR |
|
|
1e-01 |
0,962 |
0,885 |
0,850 |
0,750 |
0,963 |
0,875 |
1,000 |
1,000 |
0,998 |
0,938 |
0,945 |
0,875 |
|
1e-02 |
0,953 |
0,845 |
0,848 |
0,750 |
0,929 |
0,810 |
1,000 |
1,000 |
0,993 |
0,828 |
0,910 |
0,750 |
|
1e-03 |
0,943 |
0,773 |
0,848 |
0,748 |
0,847 |
0,718 |
0,986 |
0,813 |
0,984 |
0,788 |
0,906 |
0,748 |
|
1e-04 |
0,907 |
0,737 |
0,846 |
0,750 |
0,729 |
0,623 |
0,946 |
0,750 |
0,972 |
0,740 |
0,896 |
0,745 |
|
1e-05 |
0,816 |
0,662 |
0,792 |
0,750 |
0,642 |
0,505 |
0,847 |
0,708 |
0,835 |
0,628 |
0,811 |
0,678 |
|
Среднее |
0,916 |
0,780 |
0,837 |
0,750 |
0,822 |
0,706 |
0,956 |
0,854 |
0,956 |
0,784 |
0,893 |
0,759 |
Таблица 7
Сравнение алгоритмов по отдельным критериям
|
Ранжирование по критерию PR |
Алгоритм |
Ранжирование по критерию SR |
Алгоритм |
|
1 |
N-VMO and dADE/nrand/1 |
1 |
N-VMO |
|
2 |
SelfMMOGA |
2 |
dADE/nrand/1 |
|
3 |
PNA-NSGAII |
3 |
SelfMMOGA |
|
4 |
DE/nrand/1/bin |
4 |
PNA-NSGAII |
|
5 |
cDE/rand/1/bin |
5 |
DE/nrand/1/bin |
|
— |
— |
6 |
cDE/rand/1/bin |
Настройки SelfMMOGA следующие:
-
- максимальное число вычислений целевой функции - 50000 (для задач cecF1-cecF5) и 200000 (для cecF6-cecF8);
-
- размер общей популяции (сумма размеров популяций всех ГА) - 200;
-
- период адаптации -10 поколений 25 раз (для задач cecF1-cecF5) и 25 поколений 40 раз (для cecF6-cecF8);
-
- все стандартные параметры ГА являются само-настраиваемыми.
Как видно из табл. 5-7, SelfMMOGA демонстрирует результаты, сравнимые с известными и хорошо исследованными подходами. Он уступает алгоритмам dADE/nrand/1 и N-VMO, но стоит отметить, что эти подходы заняли на конкурсе CEC’13 2 и 4 место соответственно. В то же время среднее значение эффективности близко к первым 2 алгоритмам, превосходит PNA-NSGAII, CrowdingDE и DE, которые заняли 7, 8 и 9 места на CEC’13.
В данной работе мы включили в алгоритм только 6 базовых подходов для ММО. Тем не менее, они де монстрируют высокую эффективность, благодаря коллективной работе в ансамбле. Главной особенностью предложенного подхода является то, что он работает в автоматизированном, самоконфигурируемом режиме. Поэтому SelfMMOGA является хорошей альтернативой при решении сложных задач ММО, являющихся моделью «черного ящика».
Заключение. В работе предложен новый ГА для ММО, названный SelfMMOGA. Он базируется на метаэвристике, использующей и адаптивно управляющей несколькими разными стратегиями поиска в задачах ММО. SelfMMOGA позволяет решать сложные задачи ММО, являющиеся моделями «черного ящика», так как не использует в явном виде априорную информацию о задаче и ее свойствах. Алгоритм использует бинарное представление решений, что позволяет применять его в практических приложениях с переменными произвольного типа (включая смешанные).
На данном этапе в SelfMMOGA были включены только 6 базовых подходов ММО, чтобы показать эффективность метаэвристики. Эффективность подхода продемонстрирована на множестве тестовых задач с бинарными переменными и на задачах с вещественными переменными, представленным на глобальном конкурсе по ММО в рамках Международной конференции IEEE CEC’2013. Предложенный подход демонстрирует эффективность, сравнимую с другими известными алгоритмами.
Эксперименты показывают, что SelfMMOGA превосходит среднюю эффективность частных алгоритмов, включенных в его ансамбль. Это означает, что эффективность подхода в среднем выше, чем эффективность случайно выбранного ГА для ММО. Это свойство весьма важно для задач типа «черного ящика», так как исследователь не имеет возможности выбрать подходящий алгоритм и тонко настроить его параметры. SelfMMOGA же не требует участия эксперта и решает задачи ММО в автоматизированном, самоконфигурируемом режиме.
В дальнейших работах планируется исследовать работу SelfMMOGA с более сложными подходами в ансамбле.
Acknowledgments. The research was supported by President of the Russian Federation grant (MK-3285.2015.9).
Список литературы Самоконфигурируемый ансамбль генетических алгоритмов для решения задач мультимодальной оптимизации
- Das S., Maity S., Qub B.-Y. and Suganthan P. N. Real-parameter evolutionary multimodal optimization: a survey of the state-of-the art. Swarm and Evolutionary Computation 1, 2011, P. 71-88.
- Preuss M. Tutorial on Multimodal Optimization. In the 13th International Conference on Parallel Problem Solving from Nature, PPSN 2014. Ljubljana, 2014.
- Li X., Engelbrecht A. and Epitropakis M., Results of the 2013 IEEE CEC Competition on Niching Methods for Multimodal Optimization. Report presented at 2013 IEEE Congress on Evolutionary Computation Competition on: Niching Methods for Multimodal Optimization, 2013a.
- Liu Y., Ling X., Shi Zh., Lv M., Fang. J. and Zhang L. A Survey on Particle Swarm Optimization Algorithms for Multimodal Function Optimization. Journal of Software, 2011, Vol. 6, No. 12, P. 2449-2455.
- Deb K., Saha A. Finding Multiple Solutions for Multimodal Optimization Problems Using a Multi-Objective Evolutionary Approach. Proceedings of the 12th Conference on Genetic and Evolutionary Computation, GECCO 2010. ACM, New York, 2010, P. 447-454.
- Li X., Engelbrecht A., Epitropakis M. G. Benchmark functions for CEC’2013 special session and competition on niching methods for multimodal function optimization. Evol. Comput. Mach. Learn. Group, RMIT University, Melbourne, VIC, Australia. Tech. Rep, 2013b.
- Bessaou M., Petrowski A., Siarry P. Island Model Cooperating with Speciation for Multimodal Optimization. Parallel Problem Solving from Nature PPSN VI, Lecture Notes in Computer Science, 2000, Vol. 1917,
- P. 437-446.
- Yu E. L., Suganthan P. N. Ensemble of niching algorithms. Information Sciences, 2010, Vol. 180, No. 15, P. 2815-2833.
- Qu B., Liang J., Suganthan P.N., Chen T. Ensemble of Clearing Differential Evolution for Multi-modal Optimization. Advances in Swarm Intelligence Lecture Notes in Computer Science, 2012, Vol. 7331, P. 350-357.
- Sopov E. A Self-configuring Metaheuristic for Control of Multi-Strategy Evolutionary Search. ICSI-CCI 2015, Part III, LNCS 9142. 2015, P. 29-37.
- Singh G., Deb K. Comparison of multi-modal optimization algorithms based on evolutionary algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference, Seattle. 2006, P. 1305-1312.
- Preuss M., Wessing S. Measuring multimodal optimization solution sets with a view to multiobjective techniques. EVOLVE -A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation IV. AISC, vol. 227, Springer, Heidelberg. 2013, P. 123-137.
- Preuss M., Stoean C., Stoean R. Niching foundations: basin identification on fixed-property generated landscapes. Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, GECCO 2011. 2011, P. 837-844.
- Semenkin E. S., Semenkina M. E. Self-configuring Genetic Algorithm with Modified Uniform Crossover Operator. Advances in Swarm Intelligence. Lecture Notes in Computer Science 7331. Springer-Verlag, Berlin Heidelberg. 2012, P. 414-421.
- Molina D., Puris A., Bello R., Herrera F. Variable mesh optimization for the 2013 CEC special session niching methods for multimodal optimization. Proc. 2013 IEEE Congress on Evolutionary Computation (CEC’13). 2013, P. 87-94.
- Epitropakis M. G., Li X., Burke E. K. A dynamic archive niching differential evolution algorithm for multimodal optimization. Proc. 2013 IEEE Congress on Evolutionary Computation (CEC’13). 2013, P. 79-86.
- Bandaru S., Deb K. A parameterless-niching-assisted bi-objective approach to multimodal optimization. Proc. 2013 IEEE Congress on Evolutionary Computation (CEC’13). 2013, P. 95-102.


