Самонастраивающиеся алгоритмы стабилизации и слежения в системах управления динамическими объектами при степенных воздействиях

ствия методом автоматического масштабирования задания. Необходимость решения подобных задач возникает также в системах стабилизации и слежения за подвижными объектами.

Для управляемой замкнутой линейной стационарной системы с передаточной функцией W ( s ) изображение по Лапласу переменной x(t) имеет вид [1]:

X ( s ) = W ( s ) X о ( s ) + £ W f x ( s ) F i ( s ) + A^ ;

A ^{( s} )

где X о ( s ) и F i ( s ) изображения входного и возмущающих воздействий, W fx ( s ), i = 1, r - передаточные функции системы ⁱ по возмущениям, А_н ( s ) - полином, который определяется пред-начальными условиями переменных состояния, А ( s ) - характеристический полином передаточной функции замкнутой системы.

Изображение ошибки для произвольных воздействий при нулевых начальных условиях запишется следующим образом

r

Е ( s ) = W e ( s ) X о ( s ) + £ W f ( s ) F i ( s ) ,   (1)

i = 1

где W_e ( s ) , W ef ( s ), i = 1, r - передаточные функции системы ⁱ по ошибке, связывающие зависимость E(s) от задающего и возмущающих воздействий.

Предельное значение реакции системы на эти воздействия может быть определено по теореме о конечном значении оригинала:

Hm e ( t ) = s lim sE ( s ) .             (2)

t ^^       s ^ 0

Известны способы расчета и подавления установившейся реакции системы на задающие и возмущающие воздействия определенного типа [1, 3, 4, 5] (постоянные воздействия - X0(s) = x0, F(s) = f0, степенные воздей-ss nU a..                  f ствия общего вида X0(s) = Z“U, - F(s) = Z , u=1 s                X=1 5

nn

^X 0^{( s} ) = Z4 , F i ^(s ) = Z "T A h ( s ) = 0 .

i = 0 ^s

i = 0 ^s'

u = 1,2,..., n ; X = 1,2,..., r , воздействия в виде суммы экспонент и другие ).

Если передаточные функции по задающему и возмущающему воздействиям имеют k-кратный нулевой корень, а, например, изображения по Лапласу задающего или возмущающего воздействий - m-кратный нулевой полюс, то предельное значение ошибки системы на эти воздействия может быть определено следующим образом: skх e = lim sW (s) -m уст            е x ' m+1 , s >0

или sk f eycm = {sWef (s) m"i .(3)

s >0

При k>m – в системе нулевая статическая ошибка; при k=m – установившаяся реакция постоянна; при k – система теряет работоспособность. При степенных воздействиях общего вида количество k-кратных нулевых корней в передаточной функции разомкнутой системы должно быть не менее n, что требует для устранения статической ошибки повышения астатизма основного контура, и, как следствие, решения проблем устойчивости и преодоления трудностей, связанных с физической реализуемостью системы.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается управляемая замкнутая линейная стационарная система с передаточной функцией W ( s ) , так что X ( s ) определяется выражением (1). При этом входное - X о ( s ) и возмущающие воздействия F ( s ) изменяются по степенному закону общего вида -

Требуется построить управление, обеспечивающее: е у _Ст = °-

Задача решается методом автоматического масштабирования входного воздействия [4, 5] через организацию контура самонастройки с сигнальной адаптацией так, как это представлено на рис.1.

Пусть основной контур структуры рис.1 не содержит интегрирующих элементов, а в качестве исполнительных элементов, для простоты анализа, используются устройства с передаточными k функциями Wi(s) = —, i=1,2,™,n, реализующие s функцию интегрирования входных величин. Тогда для структуры рис. 1:

,  n-1 n - mA

Z П V" + W o ( s ) F ( s )

s  m=0 i=1.

X 0 ( s )W_pa(. s ) | 1 + X ( s ) =

11 n-1 n - mA

, (4)

e„r= lim s уст { s >0

= 0.

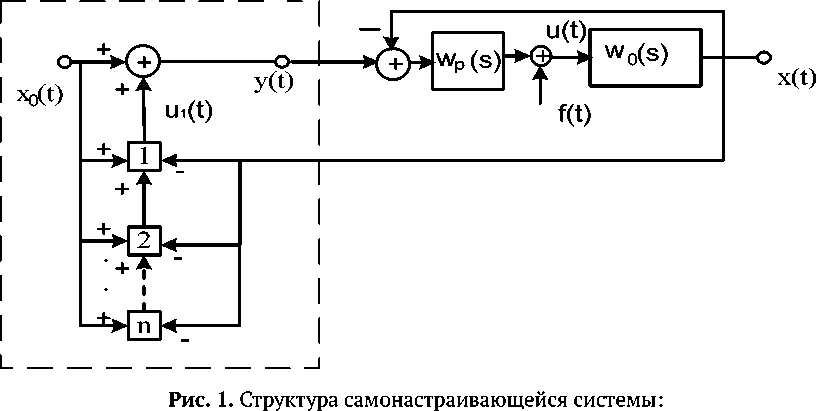
W_p ( s ) , W_o ( s ) - передаточные функции регулятора о объекта, 1,2,™,n исполнительные элементы, x 0 ( t ) - задание, x ( t ) - регулируемая переменная, u ( t ) и u i ( t ) - управления, f ( t ) - возмущение

элементов в структуре рис.1 уменьшается на степень его астатизма, а сами исполнительные элементы могут выполнять дополнительно функции усиления, дифференцирования и другие.

В системах стабилизации и слежения, помимо устранения статической ошибки и обеспечения асимптотической устойчивости, возникают также задачи синтеза законов и алгоритмов управления u(t) и u1(t) (рис.1), гарантирующих заданную точность в переходном режиме, предельное быстродействие и другие показатели, наилучшим образом согласующиеся с целями функционирования объекта [6,7,8].

Ниже, в качестве иллюстрации работоспособности структуры рис. 1 и операторов преобразования информации, приведены примеры синтеза управления линейными и нелинейными объектами и их исследование методом компьютерного моделирования. Некоторые результаты экспериментов представлены на рис. 2 и 3.

ПРИМЕР 1

Объект имеет передаточную функцию

0.5

W_n ( 5 ) =-------------- о      ( 5 + 1)(0.5 5 + 1)

, а изображения воздействий -

0.5   1    2

F ( 5 ) = ^0.1 +     X 0 ⁽ 5 ) = —+ —⁺ — , A„ ( 5 ) = -^{01 5}

5   5 ^{3                5}    5 ² 5 ^HV     0.5 5 + 1

.

Синтез оптимального регулятора основного контура системы осуществлен с использованием t критерия J = j (e2 (t) + T2e2 (t))dt, обеспечиваю-0

щего апериодические переходные процессы в основном контуре при ступенчатых воздействиях, где e(t) и e(t) - ошибка и ее производная, Т - постоянный коэффициент, равный в данном экс- перименте 0.25, так что W (5) = 6 + 25 + , а пар s раметры управления исполнительных элементов 8           8

W1 (5) = 2 + —, Wj (5) = — - назначены из условия ss гурвицевости характеристического полинома замкнутой системы.

ПРИМЕР 2

Рассматривается задача управления движением центра масс подвижного объекта, поведение которого описывается системой нелинейных дифференциальных уравнений [7, с. 129]:

x1 = x2, x2 = ax3 + bx3 , x3 =-wx3 + cu, (3) где x1 = Ah - координата центра масс, x2 = Ah(t), x3 =5 - отклонение управляющего органа, a,b,c, w - постоянные коэффициенты.

Синтез управления основного контура методом аналитического конструирования агрегированных регуляторов [8] на основе сопровождающего функционала

J = J (с 2V 2 + m 2v 2) dt с макропеременной вида

V = k 1 x 1 + k ₂ x ₂ + x ₃ ,           (4)

при с = m = 1 приводит к следующему соотношению:

u = -[k1 x1 + (k1 + k2)x2 + k2(a + bx32)x3] . (5)

Управление u переводит объект из произвольного начального состояния на притягивающее многообразие (4) с последующим устойчивым

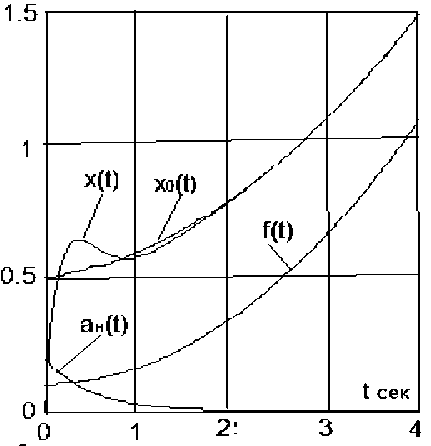
Рис. 2. Процессы в системе стабилизации и слежения:

x 0 ( t ) - задание, x ( t ) - ре гулируемая величина, f(t)- возмущение, а_н(t) - возмущение на выходе объекта

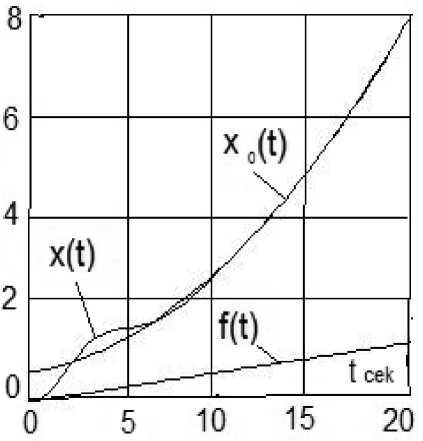
Рис. 3. Процессы в нелинейной системе:

x o ( t ) - задание, x ( t ) - регулируемая величина, f(t) - возмущение

движением вдоль него в заданное конечное состояние по траектории, являющейся одним из решений системы дифференциальных уравнений (3) с управлением (5). Включение объекта (3) в структуру рис.1 позволяет обеспечить слежение за степенным входным воздействием с нулевой статической ошибкой в условиях действия возмущений того же класса. Результаты компьютер- ного моделирования системы управления пред- ставлены на рис. 3 при следующих параметрах объекта и управления: а=2, b=0.2, c=1, w=1, k1=0.5, k2=1.5. Задающее и возмущающее воздействия изменялись по законам: x0 (t)

= 0.5 + 0.05 1 + 0.05 1 ²

f ( t ) = 0.05 t , а W 1 (s ) = 1.5 + ^0.5 , W ₂( s ) = ^0.1 .

ss

Графики процессов рис. 2 и 3 показывают, что управление в системах обеспечивает стабилизацию регулируемых координат x ( t ) с одновременным слежением за их изменением с нулевой статической ошибкой.

ВЫВОДЫ

• 1.    Исследован новый подход к формированию операторов преобразования текущей информации о задающих, возмущающих сигнальных степенных воздействиях общего вида и регулируемых координат в системах автоматического управления, обеспечивающий нулевую установившуюся реакцию систем. Предложенный метод основан на автоматическом масштабировании входного воздействия и не требует повышения астатизма основного контура замкнутой системы, а также измерения возмущений.

• 2.    Методом компьютерного моделирования

• 3.    Исследованный метод компенсации статической ошибки в системах может быть использован также для ее устранения или уменьшения при произвольных воздействиях, для которых вдали от начальной точки процессов существенное значение имеет конечное число их производных.

выявлены качественные показатели процессов в линейных и нелинейных системах и их особенности в переходном и установившемся режимах работы при степенных воздействиях, которые согласуются с результатами аналитического анализа.