Самоорганизация вуза как сложной системы

Самоорганизация присуща сложным развивающимся системам, таким как вуз, фирма, государство, общество. К изучению таких систем необходимы новые подходы, поскольку они являются нелинейными и неустойчивыми [3]. Системы этого типа более сложны, чем кибернетические системы; кроме открытости, гомеостаза, обучаемости, эти системы являются целеустремленными, адаптивными, относительно автономными (их реакции зависят не только от воздействий среды, но и от внутренних состояний).

Самоорганизующиеся системы (СОС) на основе взаимодействий с внешней средой и обработки получаемой из среды информации строят модель мира, т.е. формируют онтологию окружающего мира. Однако являясь наблюдателями в системе «СОС-среда», СОС сами воздействуют на среду. Такой наблюдатель, участвующий в обменах со средой, влияющий на нее (перцептивная петля Нейссера) характерен для функционирования СОС.

СОС непрерывно изменяются под воздействием внешней среды и, главное, под влияниями внутренней среды, понимания ее онтологической структуры и построения онтологической модели мира. В этом плане социально-экономические системы самоорганизующиеся, т.к. сохраняют устойчивость, внутреннюю гармонию, развиваются, направляя свое движение к определенным центрам притяжения - аттракторам. Основной закономерностью самоорганизации является эволюция сложных систем.

Под самоорганизацией понимается свойство сложной системы изменять свои характеристики без внешних воздействий, под влиянием целевых установок и внутренних состояний. Эти свойства самоорганизации проявляются на макроуровне в определенных эмпирических законах. Одним из них является закон Ципфа: частота появления n-го часто используемого слова обратно пропорциональна его рангу n. Такой гиперболический закон оказывается характерным для ряда сложных социальных процессов: размеров города Rn=Rо/n, где Rо - размер наибольшего города; частоты появления слов F(n)= Fо / n, где n-ранг слова, Fо - нормирующий множитель.

Проверим закон Ципфа на ряде примеров функционирования вуза. На экзамене по стратегическому управлению фирмой студенты получили следующие оценки (табл. 1).

Таблица 1 - Распределение оценок студентов

Количество	отлично	хорошо	удовлетворительно	Не удовлетворительно
Студентов	10	5	3	2
Вероятность,f	0,5	0,25	0,15	0,1
Ранги, r	1	2	3	4

Это распределение носит гиперболический характер и имеет вид: r = 0,5 /f                           (1)

На профилирующей кафедре 49 опубликованных статей за год распределились таким образом (табл. 2).

Таблица 2 - Распределение публикаций сотрудников кафедры

Количество	25	13	7	3	1
Частота, f	1	2	4	7	13
Вероятности р	0,51	0,26	0,14	0,06	0,02
Ранг, r	1	2	3	4	5

График этой функции также близок к гиперболическому распределению (рисунок 1).

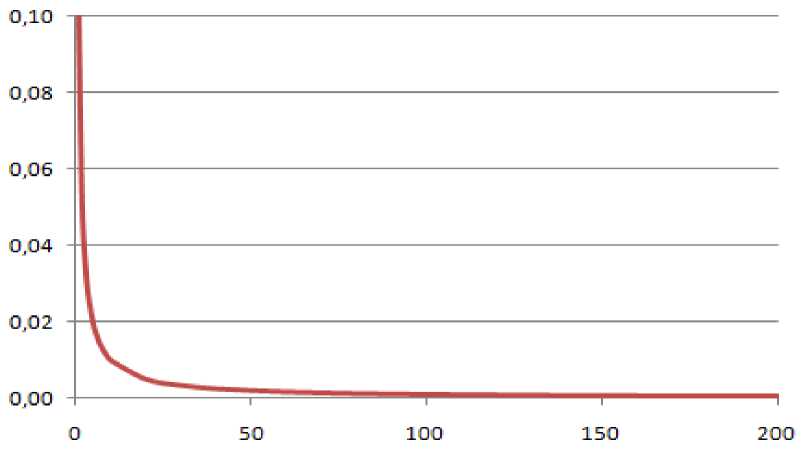
Рисунок 1 - Гиперболическое распределение Ципфа.

При этом произведение ранга на вероятность имеет примерно одинаковое значение. Интересно, что статистика дает следующее распределение умений людей: примерно 9% населения страны умеют зарабатывать деньги, 1%- имеет предпринимательский талант, 0,1%-генераторы идей, творческие личности, т.е. это распределение имеет не гауссов характер, и это может отражаться в социальных процессах. Если вероятность встретить действительно талантливого студента 0,2 (100 из 500 чел.), можно оценить инверсную частоту как:

I= lg( Общее число/ Число талантов)= lg 5= 0,7 хартли     (2)

Этот индекс будет выше у вуза, где раскрывшихся талантов будет меньше, поэтому мерой инверсной частоты лучше применить обратную величину:

i = lg (Число талантов/ Общее число)= - lg 50/500= 1,0 хартли (3)

Попробуем оценить вес ученого; если он входит в первую двадцатку из 350 преподавателей, то его показатель инверсной частоты равен:

i = - lg (20/ 350) = 1,24 хартли                                 (4)

Если учесть его частоту в множестве р= 20/350= 0,06                       (5)

то его вес будет равен:

w = i . p = 0,074                                                 (6)

Если он входит в первую десятку успешных ученых, то

I = 1,54, p=0,029, w=0,044,

Т.е. этот показатель чувствителен к рейтингу ученого и его можно использовать в рейтинговой системе.

Закон Ципфа таким образом отражает результаты процессов самоорганизации в социальных системах, свидетельствует о наличии синергетических механизмов саморегуляции, связи количественных и качественных характеристик процессов. Закон Ципфа показывает тенденцию дальнейшего увеличения удельного веса элементов, обладающих более высоким рейтингом или рангом. Эта тенденция хорошо видна на примере роста уровня образования и смещения асимметрии закона Ципфа влево. Например, в России за последние 10 лет существенно вырос накопленный образовательный потенциал и количество специалистов с высшим образованием. То же имеет место в развитых странах. По изменению моментов и асимметричности закона Ципфа можно судить о процессах самоорганизации. Если закон Ципфа рассчитывать по формуле:

U= (max x)/ rb                               (7)

где max x – наибольшая величина признака в убывающей последовательности, то параметр b характеризует степень самооргаиизации системы, уровень порядка.

Интересны рыночные интерпретации закона Ципфа: если наиболее эффективные фирмы имеют ранг 1, то лишь ½ их числа будет иметь ранг 2, соответственно 1/3 –ранг 3 и т.д. На этой основе можно строить модель рыночной ситуации. Также интересен закон Прайса, который утверждает, что число ученых y , опубликовавших 50% всех статей в вузе, равно корню квадратному из количества n ученых в вузе:

y = √ n                              (8)

Если в вузе 350 ученых (преподавателей), то число у= √ 350= 19 человек, т.е. 19 преподавателей опубликуют 50% всех работ вуза. Этот результат также свидетельствует о наличии соотношений между количеством и качеством в творческом потенциале вуза. Для перехода вуза к стратегии возрастающей отдачи необходимо наличие большего числа успешных ученых в вузе. Поэтому в американских вузах есть категория пожизненных профессоров, которые продолжают творческую работу в вузе в пенсионном возрасте. Можно отметить также фрактальный характер процессов вузе: если на уровне факультетов 20% более эффективны, то на них примерно 20% обеспечивают этот эффект, на кафедре 20% преподавателей обеспечивают результаты кафедры. Интересно, что в последнем перечне ведущих вузов России представлено только 20% от общего их общего количества («принцип Парето 20/80»). Происходит фундаментальный переворот: не человек служит развитию производства, а производство служит человеческому развитию, самосознанию.

Анализ фактов, приводимых многими авторами, показывают, что никогда еще власть и богатство не были сконцентрированы в столь немногих руках. Менее 0,5% американцев, т. е. 843 000 семей, владеют 56,2% реального имущества и 37,4% финансовых активов. Под этим слоем сверхбогатой части социума располагается слой новых работников знания. Это 3,8 млн. человек или 4% работающего населения. Они руководят цифровой экономикой высоких технологий. Доход этих 4% равняется доходу 51% (49,2 млн.) трудящихся, стоящих на нижних ступенях пирамиды доходов. К этой элите сектора знания (knowledge elite) нужно прибавить еще 16% людей, занятых интеллектуальными профессиями. Итак, все работники «отрасли знания» составляют 20% работающего населения и делят между собой половину валового социального продукта. Доходы остальных 80% населения, напротив, уменьшились, и «средний класс» значительно сократился. Согласно опросу Wall Street Journal , «более 35% молодых выпускников высшей школы вынуждены были пойти на работу, которая не требует высшего образования. Никогда еще со времен Второй мировой войны рынок труда для выпускников высшей школы не был так узок» [2].

В условиях быстро меняющейся среды предприятия возрастает важность динамического моделирования для правильного выбора решений. Существует ряд подходов к моделированию динамики процессов управления, развиваются методы динамического моделирования в когнитивном анализе.

Динамика процессов управления развитием экономических и социальных систем изучалась на основе аппарата дифференциальных уравнений и передаточных функций в теории автоматического регулирования, затем стали применяться вероятностные модели дискретных процессов, имитационные модели. В 60-х годах разработаны модели системной динамики, в 90-х - мультиагентные системы и когнитивные методы [1] (рис. 2).

Уровень абстракции

Очень высокий уровень

Высоки й уровень

Системная динамика

Имитационные модели

Средний уровень

Дискретные модели эволюции

Низкий уровень

Динамические процессы ТАР (непрерывные процессы)

Вероятностн ые процессы (дискретные)

Когнитивные методы (мультиагентное, системное дискретное моделирование,

---------------------------------------------------► 1945                    1950             1955          1960          1975-  2000Г

Рисунок 2 – Возрастание сложности динамического моделирования

Поэтому можно выделить семь динамики систем уп ра вления (рис. 3).

основных подходов

к моделированию

Имитационное моделирование динамики:

• -    структура системы - случайные переменные

Дискретные модели: - события - логика последовательно сти

Системная динамика: - структура связей - обратные связи - уравнения потоков

Мультиагентные системы:

• -    правила работы

• -    правила взаимодействия

• -    поиск решений

Система

Динамические процессы связей выходов и входов, расчеты реакций на комбинации входов:

• -    дифференциальные уравнения

• -    операционное исчисление

Вероятностные процессы:

• -    состояния элементов

• -    переходы

• -    прогнозы состояний

Нечеткая динамика:

• -    сценарии

• -    нечеткие карты

• -    нечеткие прогнозы

Рисунок 3 – Основные подходы к моделям динамики систем управления.

Таким образом, система образования, играющая стратегическую роль в развитии экономики, должна являться системой с возрастающей отдачей вложений. Процесс накопления и использования знаний в экономике можно изучать и прогнозировать методами динамического моделирования.

Для сложных социальных процессов характерна самоадаптация на базе самоорганизации, благодаря которой характеристики процесса распределяются по рангам в соответствии с существенно асимметричным законом, при этом возможен длинный хвост распределения. Кривая выживаемости вузов разных размеров имеет двустороннее распределение, показывающее уменьшение количества вузов при изменении их размеров. Среднее значение распределения показателей эффективности вузов сильно зависит от выборки. Ввиду повторяемости процессов в вузах можно говорить об их фрактальном самоподобии.