Самовоспроизводящиеся лазерные пучки и их применение стенограмма научного сообщения на совместном семинаре ИСОИ РАН и Института компьютерных исследований СГАУ 28 марта 2006 года

Рассмотрены самовоспроизводящиеся пучки с особыми свойствами. Расширено понятие самовоспроизведения для световых пучков. Рассмотрены различные приложения самовоспро-изводящихся световых пучков с особами свойствами. Особенно подробно описывается использование самовоспроизводящихся пучков в задачах манипулирования микрообъектами.

Уважаемые коллеги!

Сегодня я хочу представить доклад, систематизирующий длительный период исследований. В моем докладе можно выделить пять основных разделов, которые представлены на слайде 2.

Условия самовоспроизведения для световых пучков, формирование самовоспроизводящихся лазерных пучков с помощью дифракционных оптических элементов (ДОЭ), применение самовос-производящихся пучков в оптических информационных системах, рассмотрение сил, действующих на микрочастицы в световых пучках, и оптическое манипулирование микрочастицами с помощью самовоспроизводящихся пучков.

Простейший случай самовоспроизведения светового поля был рассмотрен Тальботом еще в 1836 году (слайд 3). В его экспериментах при освещении белым светом наблюдалось повторение цветных изображений решеток. Выражение для расстояния периодичности было получено Релеем в 1881 году.

Одновременно в моем докладе будет рассмотрено еще одно свойство световых полей – давление света (слайд 4). Впервые формулу для расчета сил светового давления получил Максвел в 1873 году. Независимо от него ту же формулу получил Бартоли в 1879 году, основываясь на законах термодинамики. В 1898 году Лебедев впервые смог экспериментально измерить силу светового давления. Появление мощных источников когерентного излучения дало сильный толчок к изучению воздействия света на микрообъекты. В 1970 году Эшкин в своих экспериментах добился устойчивого захвата микрообъекта в гауссовом лазерном пучке, В 1996 году это было сделано для вихревого светового пучка в экспериментах. В том же 1996 году было получено устойчивое вращение микрообъекта в световом пучке. В 2001 году впервые была захвачена в световом пучке группа микрообъектов.

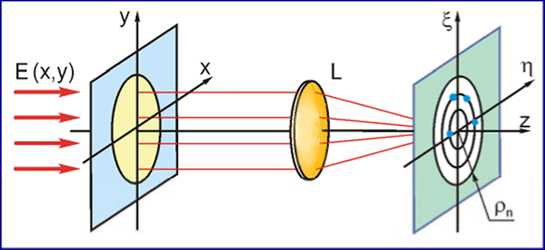
Вернемся к свойствам самовоспроизведения световых полей (слайд 5). Для самовоспроизведения светового поля с периодом z T его пространственный спектр должен лежать на кольцах Френеля радиуса r n : В качестве примера такого поля можно привести суперпозицию мод Бесселя. Если рассматривать классическое определение мод, как результат решения уравнения на собственные функции оператора, то необходимо определить еще мода Гаусса-Лагерра и Гаусса-Эрмита, которые также были использованы в исследованиях (слайд 6).

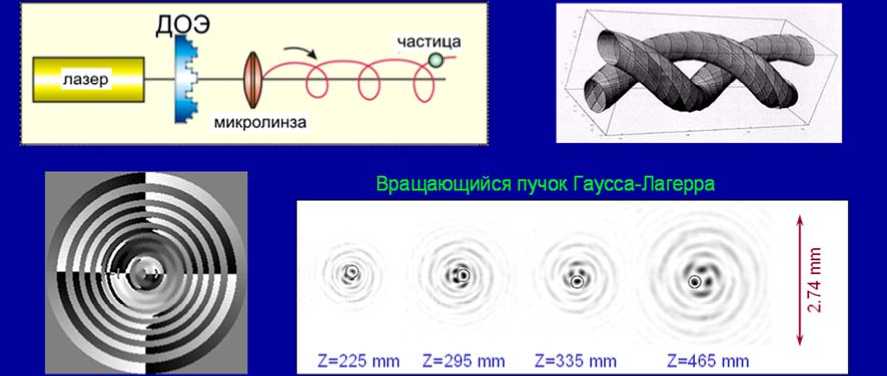
Моды обычно формируются и распространяются в некой специальной среде, но их также можно сформировать с помощью специального дифракционного оптического элемента – модана (слайд 7).

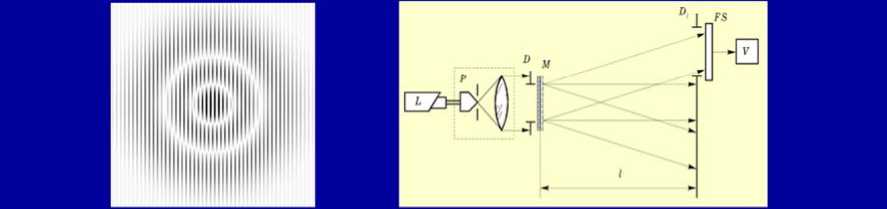
Моданы позволяют формировать не только одиночные моды, но и суперпозицию этих мод. При этом распределение интенсивности при распространении моды в пространстве может оставаться стабильным или периодически изменяться с заданным периодом (слайд 8).

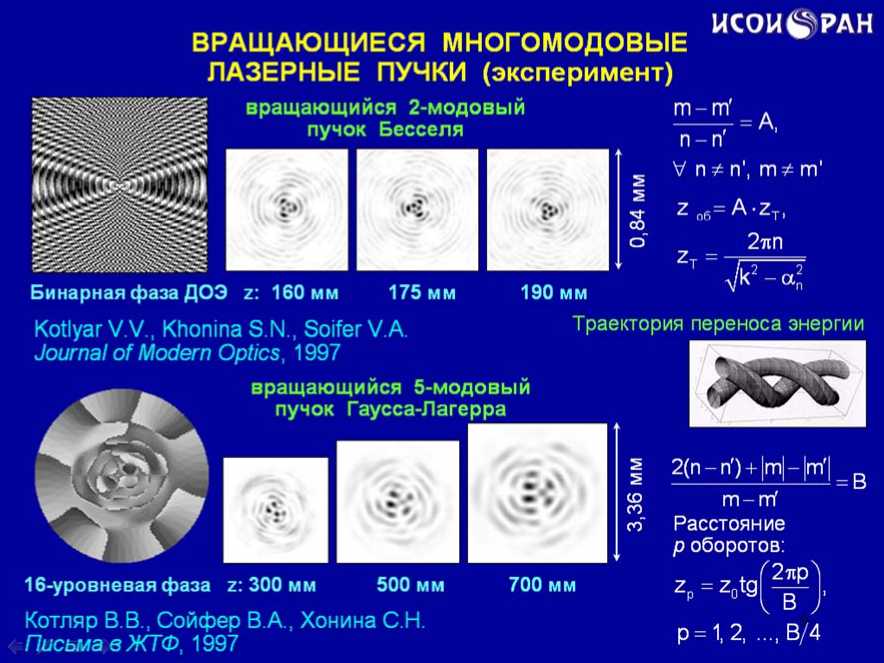
При соблюдении ряда условий можно наблюдать частный случай периодичности – вращение распределения интенсивности при распространении суперпозиции мод. При этом суперпозиция мод Бесселя вращается с постоянным периодом, а суперпозиция мод Гаусса-Лагерра вращается с переменным периодом при распространении в свободном пространстве (слайд 9).

Суперпозиция мод Гаусса-Эрмита также само-воспроизводится в пространстве с переменным периодом (слайд 10).

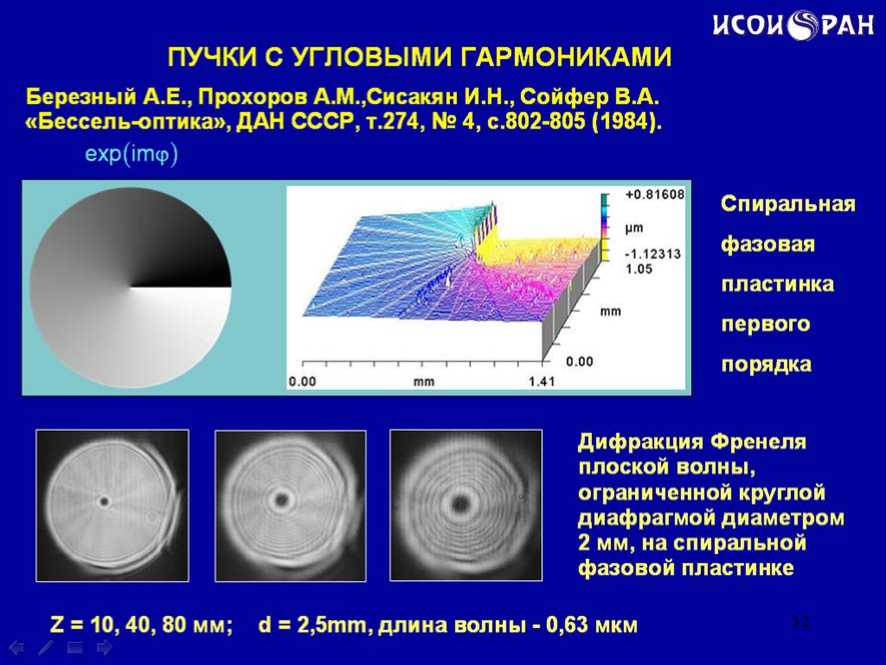
Очень важное значение имеет изучение световых полей содержащих угловые гармоники. Эти световые поля могут быть сформированы одним из трех элементов представленных на рисунке. Это либо винтовой фазовый ДОЭ, либо винтовая зонная пластина, либо решетка с развилкой (слайд 11).

На следующем слайде представлен фазовый винтовой ДОЭ и сформированное им световое поле на разных расстояниях (слайд 12).

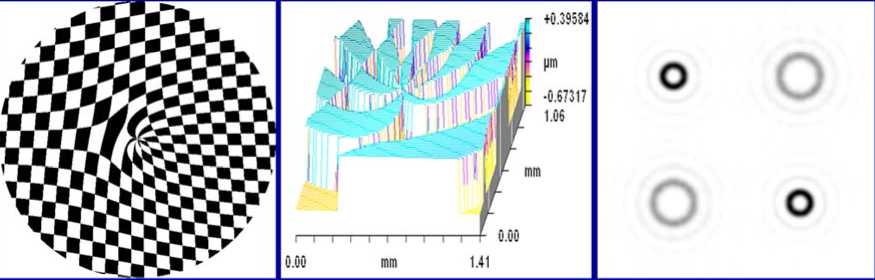
ДОЭ позволяют формировать не только одиночные световые пучки с угловыми гармониками, но также одновременно несколько световых пучков каждый из которых содержит угловую гармонику. На рисунке представлен такой ДОЭ. Он может формировать одновременно четыре пучка с угловыми гармониками –7-го, 3-го, 3-го, 7-го порядков (слайд 13).

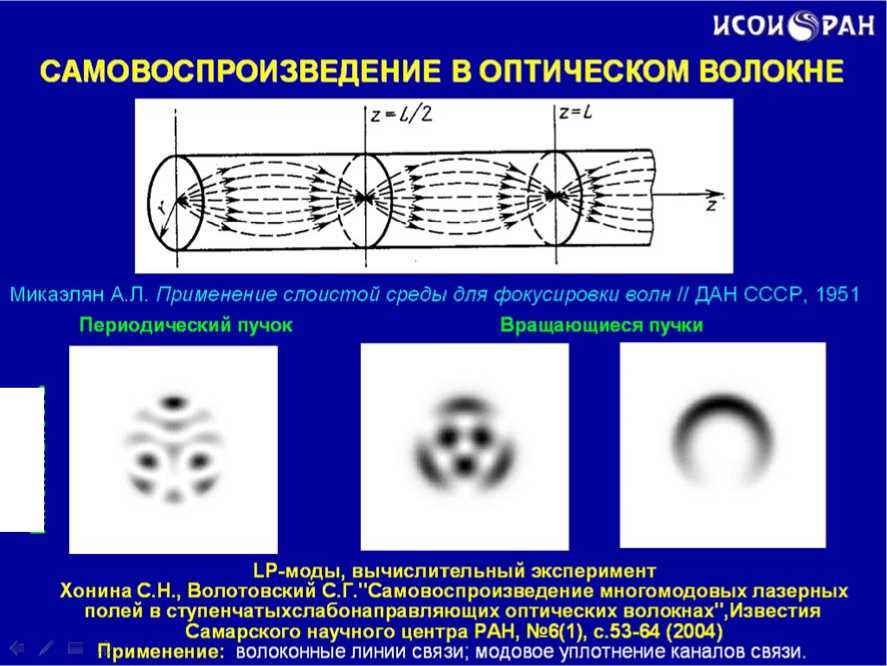
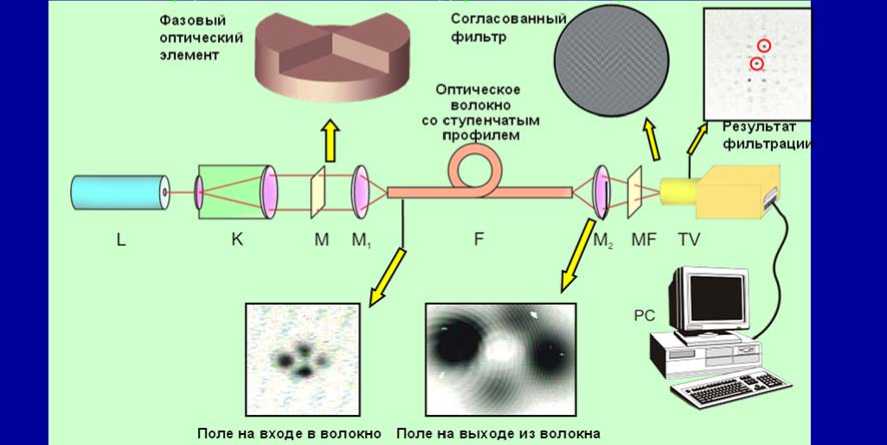
Световые пучки могут также самовоспроизво-диться при распространении внутри оптических волокон (слайд14). В результате возникает желание использовать ДОЭ формирующие модовые пучки для уплотнения каналов передачи информации по оптическим волокнам. На рисунке представлена схема эксперимента по возбуждению и селекции LP-мод в оптическом волокне. С помощью модана в волокне со ступенчатым профилем показателя преломления была возбуждена LP-мода с номером (1,1). Световое поле на выходе из волокна было подвергнуто анализу с помощь согласованного фильтра, и на месте где располагается мода (1,1), мы получили четко выраженный корреляционный пик (слайд 15).

Еще одна практическое применение световых пучков с угловыми гармониками напрямую связано с наличием у таких пучков орбитального углового момента. Орбитальный угловой момент обычно определяется для частицы имеющей отличную от нуля массу покоя и находящуюся в связанном состоянии, например электрон на электронной оболочке в атоме. Считается, что фотон не может образовывать связанные состояния, т.к. у него отсутствует масса покоя. Но световые пучки с угловыми гармониками можно считать неким аналогом связанного состояния для фотона, с одним единственным отличием, если электронные оболочки в атоме имеют сферическую симметрию, то для фотонов будет связанное состояние с цилиндрической симметрией вокруг оси распространения, и, следовательно, можно определить орбитальный угловой момент как для отдельного фотона, так и для всего пучка (слайд 16).

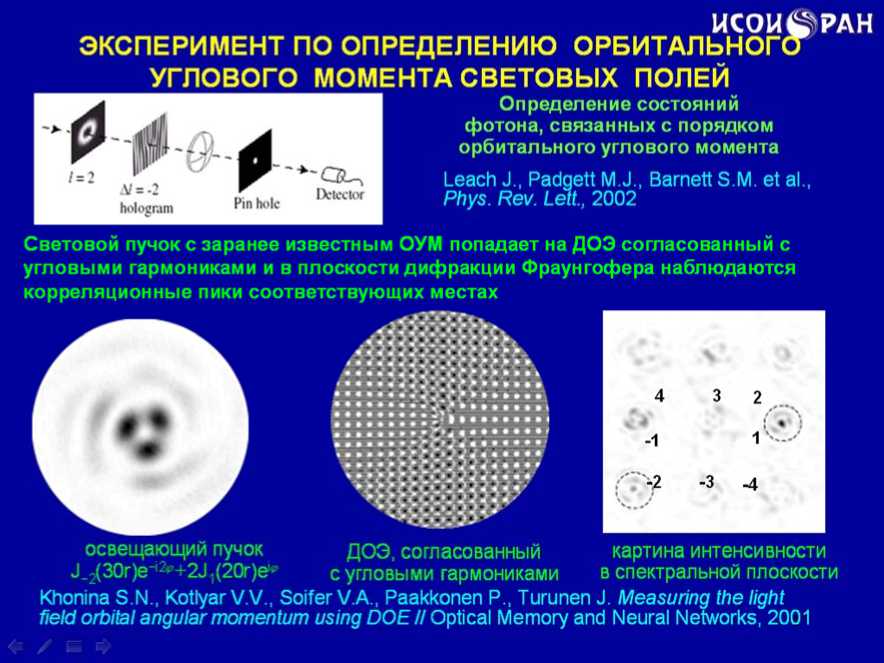
С помощью ДОЭ можно определять орбитальный угловой момент отдельных фотонов. На рисунке вы можете видеть схему такого эксперимента, в ходе которого на дифракционный элемент, формирующий световые пучки с угловыми гармониками падал пучок света с заранее известно суперпозицией мод Бесселя, а, следовательно, в этом пучке содержатся фотоны с заранее известными орбитальными угловыми моментами. После ДОЭ в Фурье-плоскости наблюдаются корреляционные пики в соответствующих местах (слайд 17).

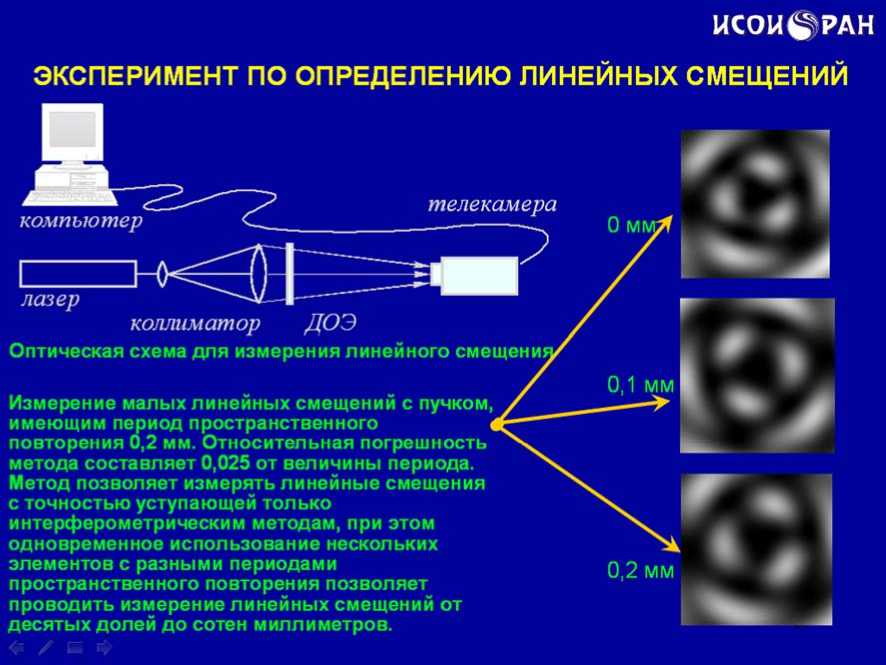
Вращение суперпозиции мод Бесселя при распространении в свободном пространстве с посто- янным периодом приводит к мысли использовать этот эффект при измерении смещений. На рисунке показана схема такого эксперимента, при котором определялось смещение непосредственно телекамеры регистрирующей распределение. Смещение измерялось погрешностью 0,025 от периода. Учитывая, что величина периода вращения может быть очень малой, этот метод способен занять промежуточное по точности измерения место между механическим и интерферометрическим методами (слайд 18).

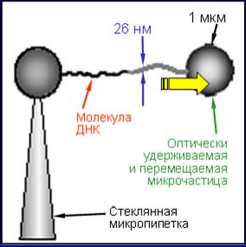
Следующее применение самовоспроизводя-щихся пучков напрямую связано с силой светового давления. Самовоспроизводящиеся пучки позволяют существенно расширить методологию «оптического пинцета» (слайд 19).

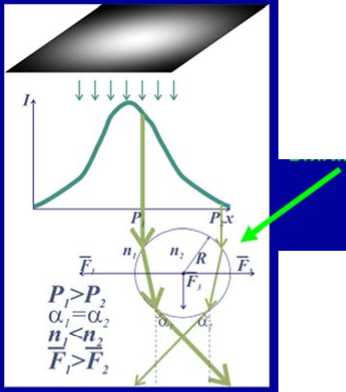
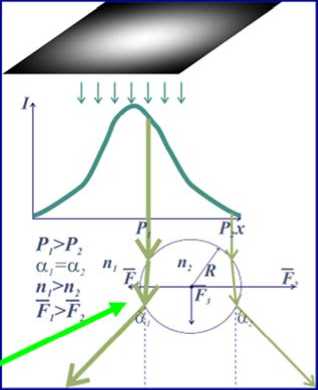
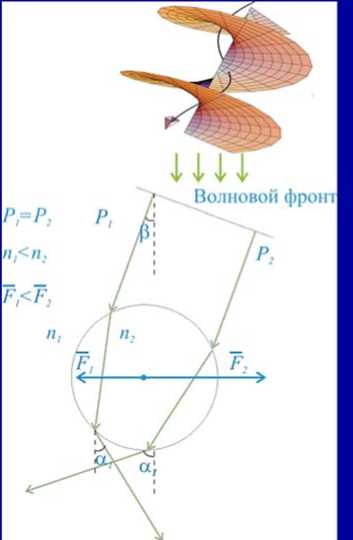
Световые пучки по-разному воздействуют на прозрачные микрочастицы. Если частица оптически более плотная чем окружающая среда, то частица будет втягиваться в область с повышенной интенсивностью. И, наоборот, менее плотная микрочастица будет выталкиваться из светового поля (слайд 20).

Если микрообъект оптически более плотный чем окружающая среда попадает в световой пучок с градиентом фазы (например, световой пучок с угловой гармоникой), то градиентная сила будет направлена против градиента фазы. Эта сила вызывает круговое движение в световых пучках с орбитальным моментом. Происходит передача орбитального момента светового пучка микрочастице. При этом энергетическая эффективность этой передачи невысока. В механическую энергию движения микрочастиц переходит не более 10-19 от общей энергии светового пучка (слайд 21).

В зависимости от видов микрочастиц и световых пучков можно составить примерную таблицу, систематизирующую способы микроманипулирования (слайд 22).

На следующем рисунке представлена примерная схема эксперимента по манипулированию микрообъектами в световом пучке сформированном ДОЭ. Оптически плотная микрочастица должна двигать вдоль линий максимальной интенсивности светового пучка (слайд 23).

А далее представлена оптическая схема и фотография реальной установки для манипулирования микрообъектами. Первоначально в этой установке использовался один и тот же микрообъектив для фокусировки излучения и наблюдения, что создавало ряд технических трудностей. В частности невозможно было менять область фокусировки. В качестве лазера использовался ЛГН-503 (слайд 24).

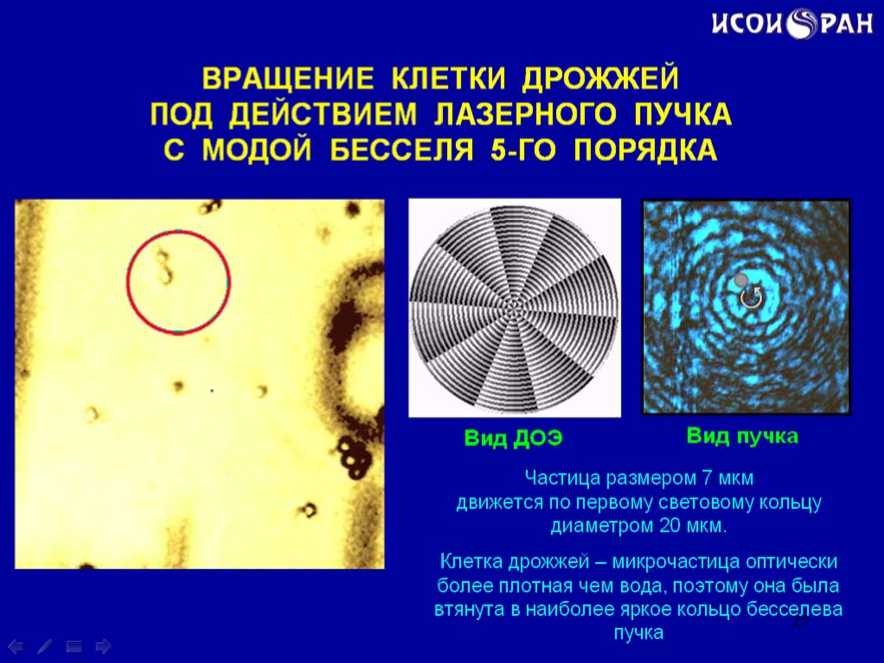
В самых первых экспериментах в качестве микрочастиц были использованы клетки дрожжей. На видеоролике показано движение клетки дрожжей в пучке Бесселя пятого порядка. При этом самого пучка не видно т.к. использован специальный светофильтр, поглощающий в зеленой области спектра (слайд 25).

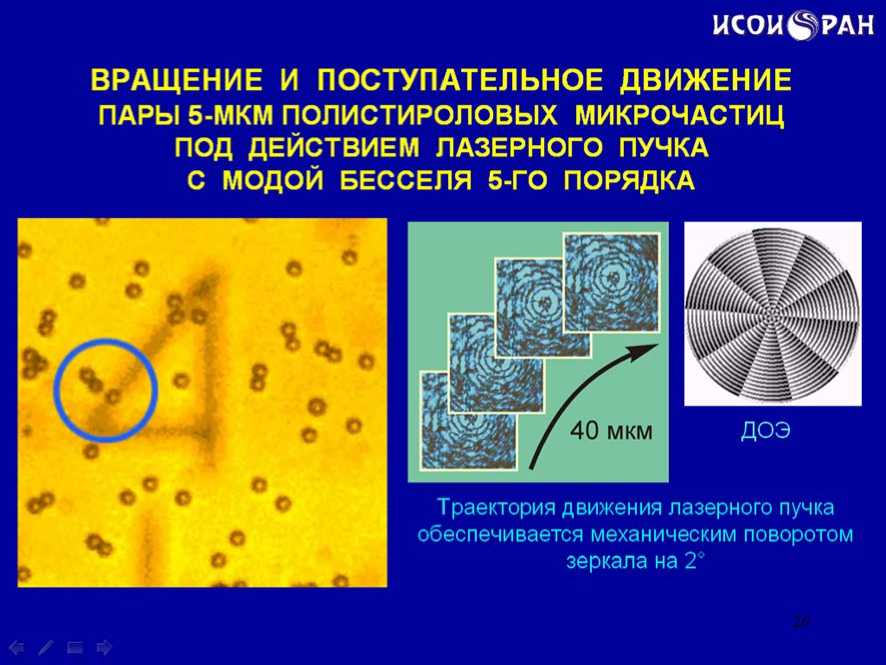
В следующем эксперименте за счет механического смещения положения фокуса пара полистироловых микрочастиц диаметром по 5мкм не только вращалась, но и перемещалась вслед за пучком (слайд 26).

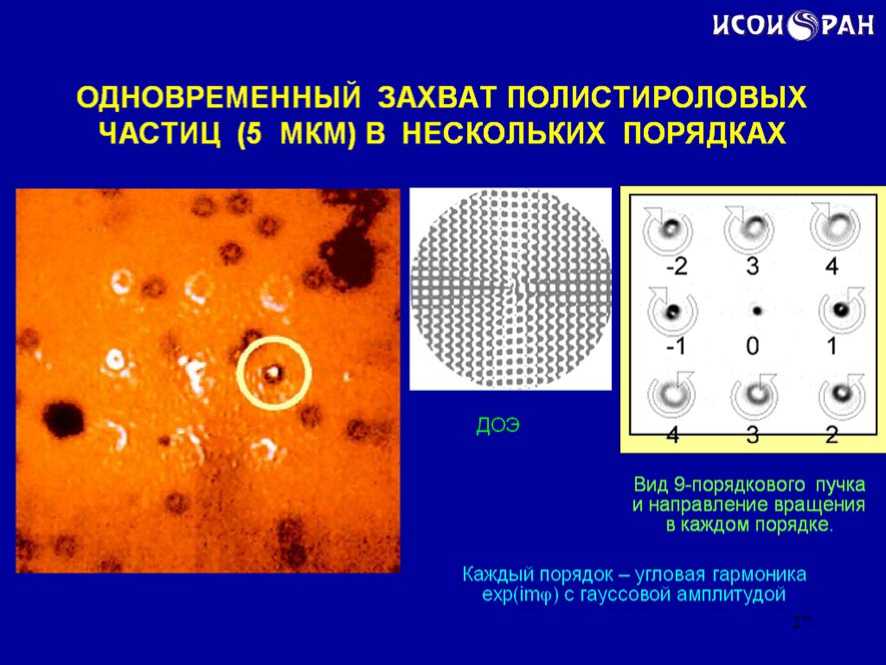
На следующем видеоролике показан эксперимент по захвату полистироловых микрочастиц из потока многопорядковым пучком с угловыми гармониками. Всего удалось захватить 4 микрочастицы в нулевом, плюс первом, минус втором и плюс четвертом порядках. При этом не удалось добиться ращения микрочастиц из-за малой мощности лазера (200 мВт) (слайд 27).

В последующих экспериментах была изменена оптическая схема. В частности для фокусировки и наблюдения использовались разные микрообъективы, а в качестве лазера был использован твердотельный лазер с длиной волны 532 нм и мощностью 500 мВт. Это позволило не только захватывать микрочастицы, но и вращать их в световом пучке, используя механизм передачи орбитального углового момента светового поля микрочастицам. При данной схеме появилась возможность одновременно наблюдать пучок и микрочастицы. Результаты экспериментов по вращению представлены в видеороликах (слайд 28).

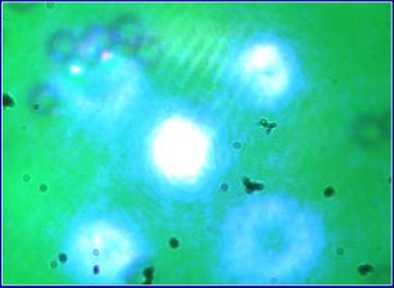
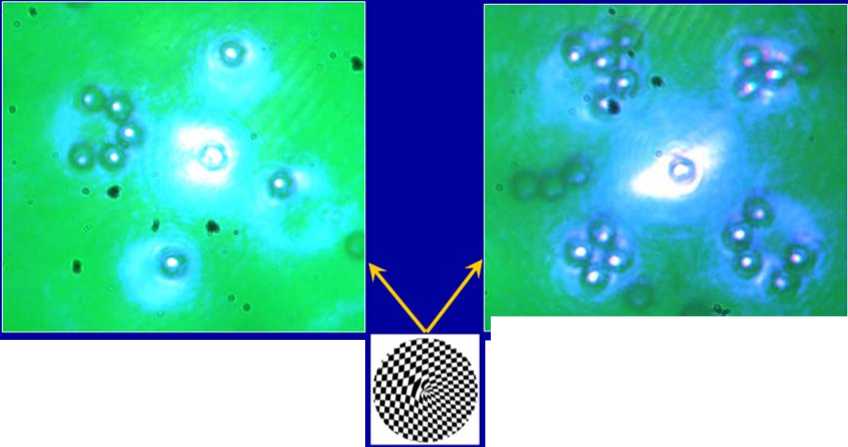
Световой пучок с угловыми гармониками, использованный в экспериментах имеет угловые гармоники разных знаков, что означает разное направление вращения в них. На следующем видеоролике представлен результат эксперимента, подтверждающий это положение. В пучках с третьей и минус третьей угловыми гармониками группы микрочастиц вращаются в разные стороны (слайд 29).

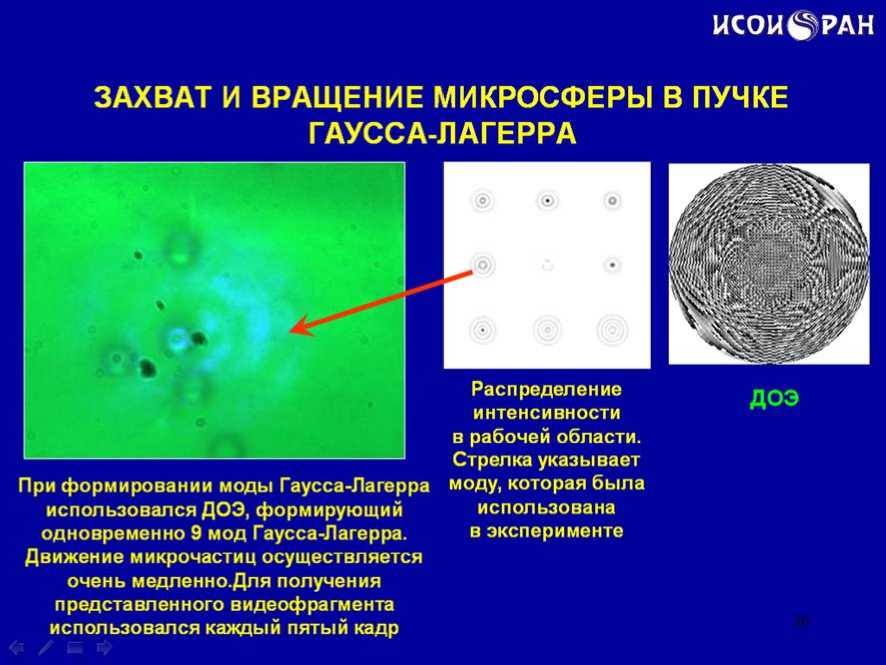
Для вращения микрочастиц использовались также моды Гаусса-Лагерра, на слайде представлен элемент, формирующий восемь мод Гаусса-Лагерра, а в видеоролике можно видеть движение микрочастицы в одном из этих пучков (слайд 30).

Для пучков Бесселя используемых при манипулировании микрочастицами было зафиксировано осаждение микрочастиц на дно кюветы, что объясняется относительной стабильностью Бесселева пучка по всей глубине кюветы (100 мкм). Если осуществлять механическое смещение кюветы можно получить ряд из микрочастиц, осажденных на дно (слайд 31).

В качестве областей применения оптического микроманипулирования следует упомянуть микробиологию, микромеханику, а также нанотехнологии (слайд 32).

Подводя итог можно сказать, что ДОЭ позволяют наиболее эффективно реализовывать следующие действия (операции) с микрочастицами:

• -    вращение проводящих и диэлектрических частиц с помощью лазерных пучков, несущих заданный орбитальный угловой момент (оптический «гаечный ключ»),

• -    захват проводящих частиц в 3D световую полость (оптическая «бутылка»),

• -    перемещение прозрачных диэлектрических микрочастиц по заданной 3D траектории (оптический «гид»),

• -    одновременное однотипное манипулирование несколькими микрочастицами, захваченными вдоль оптической оси Бесселевого пучка (оптический «вал»),

• -    одновременное разнотипное манипулирование несколькими микрочастицами, захваченными в различных точках пространства с помощью многопорядковых ДОЭ (матричный оптический «привод»),

• -    отклонение движения микрочастиц определенного размера от прямолинейного с помощью светового поля с поперечно-периодической структурой (оптический «сепаратор»).

Спасибо за внимание.

UCOU^PAH

САМОВОСПРОИЗВОДЯЩИЕСЯ ЛАЗЕРНЫЕ ПУЧКИ И ИХ ПРИМЕНЕНИЕ

Сойфер ВЛ., Котляр В.В., Хонина С.Н., Скиданов Р.В.

ИНСТИТУТ СИСТЕМ ОБРАБОТКИ ИЗОБРАЖЕНИЙ РАН

исои

РАН

Слайд 1

ИСОИ^РАН

ПЛАН ДОКЛАДА

• •    Введение: эффект Тальбота, условия самовоспроизведения

• •    Формирование самовоспроизводящихся лазерных пучков с помощью дифракционных оптических элементов (ДОЭ)

• •    Применение в оптических информационных системах

• • Силы действующие на микрочастицы в световых пучках

•Оптическое манипулирование микрочастицами с помощью самовоспроизводящихся пучков

• •    Заключение

UCOU^PAH

ПЕРИОДИЧЕСКОЕ САМОВОСПРОИЗВЕДЕНИЕ ПОПЕРЕЧНО-ПЕРИОДИЧЕСКИХ ПОЛЕЙ

Эффект Тальбота

Длина волны X Период d

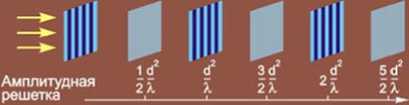
W.H.F. Talbot, Facts relating to optical sciences П Phil. Mag., 1836 (при освещении белым светом наблюдалось повторение цветных изображений решеток)

ZT = 2d2/X - период Тальбота Lord Rayleigh, Phil. Mag., 1881 (получено расстояние периодичности)

самовоспроизведение суперпозиции плоских волн

Е(х)=^Спехр i2nnx d

, d - поперечный период

_ _ 2d2	d2	d2 — ___	7
X	X 2	- 2Х 4	i NX 2N
полное повторение	поперечный сдвиг на d/2	сложение исходного и сдвинутого изображений FFFFF ЕЕЕЕЕ LLLLLЕЕЕЕЕ	сложение N сдвинутых копий исходного изображения

Слайд 3

ИСОИ^РАН

СИЛА ДАВЛЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

1873г - расчет светового давления в рамках электродинамике(Дж. Максвелл)

1879г- расчет светового давления в рамках термодинамики(А Бартоли)

1898г- опыты по измерению светового давления (П.П. Лебедев)

1970г- захват микрообъектов в лазерных пучках (А Эшкин )

1996г- захват микрообъектов в вихревых световых пучках (К. T-Gahagan)

1996г- вращение микрообъекта в вихревых световых пучках полученных с помощью амплитудных голограмм (М. Е Friese. )

2001г. - использование ДОЭ для оптического захвата группы микрообъектов(У.Ogura)

2004г-использование многопорядковых ДОЭ для оптического захвата и

Вращения микрообъектов (В. А. Сойфер)

UCOU^PAH

УСЛОВИЯ САМОВОСПРОИЗВЕДЕНИЯ СВЕТОВЫХ ПОЛЕЙ В СВОБОДНОМ ПРОСТРАНСТВЕ

Для самовоспроизведения светового поля с периодом z_T его пространственный спектр должен лежать на кольцах Френеля радиуса р_п:

Это обратная задача Montgomery W.D. (J. Opt. Soc. Am., 1967)

P = ^7 +W

Суперпозиция Бесселевых пучков : Е(г,ф) = У J_m(a_nr)exp(im

■"Де a„ = Vk’" nW. k = Т Л г = Vx2 + У2

у

Ф = arctg-х

Слайд 5

UCOU^PAH

СИНТЕЗИРОВАННЫЕ НА КОМПЬЮТЕРЕ ГОЛОГРАММЫ ДЛЯ ФОРМИРОВАНИЯ МОДОВЫХ ПУЧКОВ (моданы)

1. Голуб М.А., Прохоров А.М., Сисакян И.Н., Сойфер В.А. Синтез пространственных фильтров для исследования поперечного модового состава когерентного излучения И Квантовая электроника, 1982.

Кодирование на основе несущей пространственной частоты

2 Bartelt Н.О., Lohmann A.W., Freude W., Grau G. К. Mode analysis of optical fibers using computer-generated matched filters II Electronic Letters, 1983.

Слайд 7

Бинарная фаза ДОЗ

50 мм

UCOU^PAH

САМОВОСПРОИЗВЕДЕНИЕ ПУЧКОВ БЕССЕЛЯ Jm(anr) ехр(|тф) (эксперимент)

Суперпозиция Бесселевых пучков: Е(г,ф) = У J_m(a_nr)exp(imq)),

СТАБИЛЬНЫЙ: a_n=const Vm

2-модовый пучок Бесселя: J 3 (120,5r)e-'3’ + J3 (120,5г)е|3ф,гт =0

ПЕРИОДИЧЕСКИЙ: a₁(z_T)T11(z_T) Vm

3-модовый пучок Бесселя:

J -.(50.44г)е"2ф + Jo (83.27г) + J2 (50.44r) el?v,zT = 20мм

Бинарная фаза ДОЗ z: 85 мм 90 мм        95 мм       105 мм

1. Котляр В.В., Сойфер В.А., Хонина С.Н. Квантовая электроника, 1991

2. Kotlyar V.V, Khonina S.N., Soifer V.A. Journal of Modern Optics, 1995

3. Khonina S.N., Kotlyar V.V., Soifer V.A., Lautanen J., Honkanen M., Turunen J. Optik, 1999

80 мм

60 мм

70 мм

0,83 мм               0,71 mm

Слайд 8

16-уровневая фаза

z: 300 мм

500 мм

700 мм

AzTl 2лП

Расстояние р оборотов:

Котляр В. В., Сойфер В А, Хонина С.Н Письма в ЖТФ, 1997

ВРАЩАЮЩИЕСЯ МНОГОМОДОВЫЕ ИС0М^РАН

ЛАЗЕРНЫЕ ПУЧКИ (эксперимент) вращающийся 2-модовый           m-m' _д

§        пучок Бесселя                      < ~А>

Kotlyar V.V., Khonina S.N., Soifer V А.

Journal of Modern Optics, 1997

вращающийся 5-модовый

^^^       пучок Гаусса-Лагерра

Бинарная фаза ДОЗ z: 160 мм 175 мм

190 мм             v п

Траектория переноса энергии

Слайд 9

UCOU^PAH

САМОВОСПРОИЗВЕДЕНИЕ МНОГОМОДОВЫХ ПУЧКОВ ГАУССА-ЭРМИТА

8^И QE3H

I______________________________________________________________________I___________________________________________I________________________________________________________I

0            21 мм 32 мм 50 мм

Многомодовый лазерный пучок самовоспроизводится

(с точностью до масштаба) с переменным интервалом:

Г

, .                 . । 2 Til z (z) = z + z tg —

⁷             0 I p

1 = 1, 2,3,..., p = (m-m') + (n-n'), (m,n)-номера мод

Хонина C.H., Котляр В.В., Сойфер В.А. Письма в ЖТФ, 1999

«ВИНТОВЫЕ» ДИФРАКЦИОННЫЕ ОПТИЧЕСКИЕ ЭЛЕМЕНТЫ (ДОЭ) для формирования вращающихся полей

UCOU^PAH

Винтовой фазовый ДОЭ exp(im

Винтовая зонная пластина sgnfcos(mv+kr²)]

Решетка с «вилкой»

sgn[cos(m

• 1.    Березный А.Е., Прохоров А.М., Сисакян И.Н., Сойфер В.А. Бессель-оптика //ДАН, 1984.

• 2.    Khonina S.N., Kotlyar V.V., Shinkaryev M.V., Soifer V. А., Uspleniev G.V., The phase rotor filter //J Modern Optics, 1992

1. Heckenberg N.R. et al. Generation of optical phase singularities by computer-generated holograms //Opt. Lett., 1992

1. Bazhenov V. Yu., Soskin M.S., Vasnetsov M.V. Screw dislocations in light wavefronts //J. of Mod. Opt, 1992

Слайд 11

UCOU^PAH

ДОЭ ДЛЯ ФОРМИРОВАНИЯ СВЕТОВЫХ ПУЧКОВ С УГЛОВЫМИ ГАРМОНИКАМИ

Фаза ДОЭ                  Центральная часть          Распределение интенсивности

±/3<р    ±z'7 ф            микрорельефа ДОЭ         в зоне дифракции Фраунгофера

С j С                                          после ДОЭ

ДОЭ формирует 2 световых кольца с угловыми гармониками 3-го порядка (малые кольца) и 2 световых кольца с угловыми гармониками 7-го порядка (большие кольца).

Слайд 13

Интенсивность

z-L/2.

МСОИ^РАН

САМОВОСПРОИЗВЕДЕНИЕ В ОПТИЧЕСКОМ ВОЛОКНЕ

Микаэлян А.Л. Применение слоистой среды для фокусировки волн И ДАН СССР, 1951

Периодический пучок

Вращающиеся пучки

LP-моды, вычислительный эксперимент

ХонинаС.Н., Болотовский С.Г."Самовоспроизведение многомодовых лазерных полей в ступенчатыхслабонаправляющих оптических волокнах",Известия Самарского научного центра РАН, №6(1), с.53-64 (2004) Применение: волоконные линии связи; модовое уплотнение каналов связи.

Слайд 14

ВОЗБУЖДЕНИЕ И СЕЛЕКЦИЯ UCOU^PAH МОД ОПТИЧЕСКОГО ВОЛОКНА

Используя свойство пучков Гаусса-Эрмита воспроизводится в свободном пространстве с точностью до масштаба можно возбудить в волокне одновременно до 5-6 LP-мод, а затем на выходе селектировать их с помощью согласованного с этими модами фильтра. Оптическое волокно имеет ступенчатый профиль показателя преломления с диаметром сердцевины 9.3 мкм и диаметром оболочки 125 мкм. Числовая апертура NA 0.3, длина волны отсечки 1270 нм. Длина волокна 1.5 метра. На торцы волокна вклеены стандартные коннекторы типа FC.

rxmv р = йк Импульс отдельного фотоне

ОРБИТАЛЬНЫЙ УГЛОВОЙ МОМЕНТ (ОУМ) МС0М^РАН СВЕТОВОГО ПОЛЯ

J = LMT 1 (м2кгс1) размерность орбитального углового момента перпендикулярная к Pi = Йк±направлению распространения составляющая импульса

J = [rxp±] ОУМ отдельного фотона

ОУМ отдельного фотона принимает дискретные значения IJ1= 0;л;2л;Зл... соответствующие угловым гармоникам

О;^;^'2^;^-3^

момент количества движения, может быть определен также и для фотонов, как для частиц обладающих ненулевым импульсом с Re[Ex Н И аналог орбитального углового

8л       J момента для электромагнитного поля

Слайд 15

hologram l । Detector Pin hole

Khonina S.N., Kotlyar V.V., Soifer V.A., Paakkonen P„ Turunen J. Measuring the light field orbital angular momentum using DOE H Optical Memory and Neural Networks, 2001

ДОЗ, согласованный с угловыми гармониками освещающий пучок

JJ30r)e-'2₽+2J1(20r)el картина интенсивности в спектральной плоскости

Световой пучок с заранее известным ОУМ попадает на ДОЗ согласованный с угловыми гармониками и в плоскости дифракции Фраунгофера наблюдаются корреляционные пики соответствующих местах

UCOU^PAH

ЭКСПЕРИМЕНТ ПО ОПРЕДЕЛЕНИЮ ОРБИТАЛЬНОГО УГЛОВОГО МОМЕНТА СВЕТОВЫХ ПОЛЕЙ

Определение состояний

А                                фотона, связанных с порядком

Н^И<                 орбитального углового момента

Leach J„ Padgett M.J., Barnett S.M. et al.,

Phys. Rev. Lett., 2002

Слайд 17

0 мм

UCOU^PAH

ЭКСПЕРИМЕНТ ПО ОПРЕДЕЛЕНИЮ ЛИНЕЙНЫХ СМЕЩЕНИЙ компьютер лазер коллиматор ДОЗ

Оптическая схема для измерения линейного смещени

Измерение малых линейных смещений с пучком, имеющим период пространственного         < повторения 0,2 мм. Относительная погрешность метода составляет 0,025 от величины периода. Метод позволяет измерять линейные смещения с точностью уступающей только интерферометрическим методам, при этом одновременное использование нескольких элементов с разными периодами пространственного повторения позволяет проводить измерение линейных смещений от десятых долей до сотен миллиметров.

0,2 ММ телекамера

I I I I I I I

F=W(1*R)/c

P=4x10 H co О m=0 04 мг mg

60 Вт

ПСОМ^PAH СИЛЫ ВОЗДЕЙСТВИЯ СВЕТА НА ВЕЩЕСТВО

(ДАВЛЕНИЕ СВЕТА)

Сила давления света F=W(1+R)/c

Формула верна при нормальном падении света на поверхность.

W - количество падающей в секунду энерги R - коэффициент отражения поверхности (R=0 - поглощающая поверхность, R=1 - отражающая поверхность), с - скорость распространения световых луч!

Максвелл, 1873; Бартоли, 1879 (теория)

Лебедев, 1898 (эксперимент)

Оптический «пинцет»

Оптический «пинцет» предназначен для удерживания прозрачных микрообъектов.

Кроме сил светового давления, в методе оптического «пинцета» используются также градиентные силы

Слайд 19

UCOM^PAHСИЛЫ ВОЗДЕЙСТВИЯ СВЕТА НА ВЕЩЕСТВО

Оптически менее плотный объект (пузырек воздуха) -возникает сила выталкивания

(градиентные)

Оптически более плотный объект (полистироловый микрошар) -возникает сила втягивания

Если световой пучок попадает на прозрачный микрообъект, то возникает градиентная сила вызванная изменением суммарного импульса светового пучка после преломления на микрообъекте. Также будет присутствовать относительно небольшая составляющая силы F₃ направленная по световому пучку, обусловленная наличием френелевского отражения (давление света).

UCOU^PAH ПЕРЕДАЧА ОРБИТАЛЬНОГО МОМЕНТАСВЕТОВОГО ПУЧКА МИКРОЧАСТИЦЕ

Если микрообъект оптически более плотный чем окружающая среда попадает в световой пучок с градиентом фазы (например световой пучок с угловой гармоникой), то градиентная сила будет направлена против градиента фазы. Эта сила вызывает круговое движение в световых пучках с орбитальным моментом. Происходит передача орбитального момента светового пучка микрочастице.

При этом энергетическая эффективность этой передачи невысока. В механическую энергию движения микрочастиц переходит не более 1019 от общей энергии светового пучка.

Слайд 21

ТИПЫ ЧАСТИЦ И СВЕТОВЫХ ПУЧКОВ UCOU^PAH ДЛЯ РАЗЛИЧНЫХ СПОСОБОВ МАНИПУЛИРОВАНИЯ

	20-5 мкм	5 - 1 мкм				1 - 0.01 мкм наночастицы		10"3 . ю-9 мкм атомы, ионы. молекулы
	Прозрачные полые (градиентные силы выталкивания)	Прозрачные плотные (градиентные силы втягивания)	Двупере-ломляющие		Непрозрачные (силы светового давления)
	3D захват в min интенсивности (Ga hag ап. 1996, сфокусированный винтовой Гауссов пучок) Продольный захват нескольких объектов (Garces-Chavez. 2002, Бесселев пучок) 2D захват и вращение (Garces-Chavez. 2002. винтовой Бесселев пучок) (передача орбитального момента)	Ускорение (Ashkin. 1970. Гауссов пучок) 3D захват в max интенсивности (Ashkin. 1986. сфокусиров Гауссов пучок) 2D. 3D захват и перемещение (Reicherter. 1999, Liesener, 2000, динамический транспарант, сфокусированный Гауссов пучок) 2D. 3D захват и вращение (Paterson. 2001, винтовой сфокусированный Гауссов лучок) Продольный захват нескольких объектов (Artt, 2001. Garces-Chavez, 2002, Бесселев пучок) Захват нескольких объектов и их независимое перемещение (Curtis. 2002, Enksen, 2002. Rodrigo. 2002, динамический транспарант. матрица сфокусированных Гауссовых фунд или винтовых пучков)	3D захват в max интенсивности и вращение (Friese. 1998, 2001. Moothoo-2001. Гауссов пучок с круговой поляризацией)		3D захват в min интенсивности и вращение (Не. 1995, винтовой Гауссов nynoK.Fnese, 1996;Simpson, 1997, винтовой Гауссов пучок с круговой поляризацией)	3D захват кварцевой частицы 26нм (Ashkin. 1986, сфокусированный Гауссов пучок) Захват металлической частицы Збнм (Svoboda. 1994. интерференция двух сфокусированных Гауссовых пучок)		Торможение, охлаждение, концентрация (Летохов, Миногин, Балякин, 19681990, Ashkin, Bjorkholm, Chu, 1970-1988)
				Лазеры: -    достаточная мощность : 50- 200 мВт -    диапазон длин волн : 0.38 - 1,06 мкм

UCOU^PAH

ОПТИЧЕСКИЙ ЗАХВАТ И МАНИПУЛИРОВАНИЕ МИКРООБЪЕКТАМИ

Фаза ДОЗ

Применения:

• -    захват и манипулирование в нанотехнологиях и биофизике;

• -    генерация разрядов заданной пространственной структуры в жидкостях и газах; - бесконтактное измерение расстояний и скорости.

Слайд 23

Светофильтр

МСОИ^РАН

Фото оптической установки

Оптическая схема

Аргоновый лазер

Кювв а с микрочастицами

Осветитель

Для устойчивого захвата микрочастиц размером 5мкм необходима интенсивность в рабочей области >108 Вт/м2 в эксперименте используется аргоновый лазер с длиной волны 0,51 мкм и мощностью 200 мВт, для фокусировки излучения используется оптическая система микроскопа Биолам-М, для поглощения лазерного излучения перед телекамерой устанавливался светофильтр поглощающий световое излучение с длиной волны в диапазоне от 490 нм до 525 нм, что позволило наблюдать движение микрочастиц, при это лазерное излучение полностью отфильтровывалось.

ОПТИЧЕСКАЯ СХЕМА ДЛЯ МАНИПУЛИРОВАНИЯ МИКРООБЪЕКТАМИ

UCOU^PAH

Вид пучка

Вид ДОЭ

ВРАЩЕНИЕ КЛЕТКИ ДРОЖЖЕЙ ПОД ДЕЙСТВИЕМ ЛАЗЕРНОГО ПУЧКА С МОДОЙ БЕССЕЛЯ 5-ГО ПОРЯДКА

Частица размером 7 мкм движется по первому световому кольцу диаметром 20 мкм.

Клетка дрожжей - микрочастица оптически более плотная чем вода, поэтому она была втянута в наиболее яркое кольцо бесселева пучка

Слайд 25

40 мкм доэ

Траектория движения лазерного пучка обеспечивается механическим поворотом зеркала на 2°

МСОИ^РАН

ВРАЩЕНИЕ И ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ПАРЫ 5-МКМ ПОЛИСТИРОЛОВЫХ МИКРОЧАСТИЦ ПОД ДЕЙСТВИЕМ ЛАЗЕРНОГО ПУЧКА С МОДОЙ БЕССЕЛЯ 5-ГО ПОРЯДКА

UCOU^PAH

ОДНОВРЕМЕННЫЙ ЗАХВАТ ПОЛИСТИРОЛОВЫХ ЧАСТИЦ (5 МКМ) В НЕСКОЛЬКИХ ПОРЯДКАХ

ДОЭ

Каждый порядок - угловая гармоника exp(im

Вид 9-порядкового пучка и направление вращения в каждом порядке.

Слайд 27

МСОИ^РАН

ОДНОВРЕМЕННЫЙ ЗАХВАТ И ВРАЩЕНИЕ ГРУППЫ МИКРОЧАСТИЦ В СВЕТОВЫХ ПУЧКАХ С УГЛОВЫМИ ГАРМОНИКАМИ

Вращение пяти полистироловых микросфер в световом пучке с угловой гармоникой 7-го порядка

ДОЭ

Вращение шести полистироловых микросфер в световом пучке с угловой гармоникой 7-го порядка

ИСОИ^РАН

ОДНОВРЕМЕННЫЙ ЗАХВАТ И ВРАЩЕНИЕ ГРУППЫ МИКРОЧАСТИЦ В РАЗНЫХ ПОРЯДКАХВ СВЕТОВЫХ ПУЧКАХ С УГЛОВЫМИ ГАРМОНИКАМИ

Вращение пяти полистироловых микросфер в световом пучке с угловой гармоникой 7-го поряцка и одновременный захват микросфер в других порядках

ДОЭ

Вращение нескольких групп полистироловых микросфер в световых пучках с угловыми гармониками 3-го порядка (малые кольца) и 7-го порядка (большие кольца)

Слайд 29

МСОИ^РАН

ЗАХВАТ И ВРАЩЕНИЕ МИКРОСФЕРЫ В ПУЧКЕ ГАУССА-ЛАГЕРРА

ДОЭ

При формировании моды Гаусса-Лагерра использовался ДОЭ, формирующий одновременно 9 мод Гаусса-Лагерра.

Движение микрочастиц осуществляется очень медленно.Для получения представленного видеофрагмента использовался каждый пятый кадр

Распределение интенсивности в рабочей области. Стрелка указывает моду, которая была использована в эксперименте

UCOU^PAH

ЗАХВАТ И ОСАЖДЕНИЕ ГРУППЫ МИКРОЧАСТИЦ В ПУЧКЕ БЕССЕЛЯ ПЯТОГО ПОРЯДКА ИЗ ВОДНОЙ СУСПЕНЗИИ

После фокусировки пучка микросферы начинают движение по кругу, но с осаждением и захватом все большего количества микросфер круговое движение прекращается.

Слайд 31

ОБЛАСТИ ПРИМЕНЕНИЯ UCOU^PAHОПТИЧЕСКОГО МАНИПУЛИРОВАНИЯ

Биология

эксперимент по измерению упругих сил молекулы ДНК

Wuite GJ, Smith SB, Young M, Keller D, Bustamante C. // Nature, 2000

Bao X R , Lee H.J., Quake

S .R . // Phys. Rev. Lett., 2003

Микромеханика

передача в жидкости вращательного момента, полученного двулучепреломляющей частицей от пучка с круговой поляризацией

Friese M.E.J. et al, Optically driven micromachine elements П Appl. Phys. Let., 2001

Нанотехнологии

Korda P.T., Spalding G.C., and Grier D.G. Nanofabrication with

Holographic Optical Tweezers H Rev. Sci. Instruments, 2002

Chaumet, P.O., Rahmani A., and Nieto-Vesperinas M., Optical trapping and manipulation of nano-objects with an apertureless probe // Physical Review Letters, 2002

Ignatovich F. and Novotny L.

Experimental study of nanoparticle detection by optical gradient forces

H Rev. Sci. Instr., 2003

Sandoghdar V. et al, Scanning near-field optical studies of photonic devices

H Photonic crystals, Wiley-VCH, Germany, 2004

UCOU^PAHЗАКЛЮЧЕНИЕ

ДОЭ позволяют наиболее эффективно реализовывать следующие действия (операции) с микрочастицами:

• •    Вращение проводящих и диэлектрических частиц с помощью лазерных пучков, несущих заданный орбитальный угловой момент (оптический "гаечный ключ")

• •    Захват проводящих частиц в 3D световую полость (оптическая "бутылка")

• •    Перемещение прозрачных диэлектрических микрочастиц по заданной 3D траектории (оптический "гид")

• •    Одновременное однотипное манипулирование несколькими микрочастицами, захваченными вдоль оптической оси Бесселевого пучка (оптический "вал")

• •    Одновременное разнотипное манипулирование несколькими микрочастицами, захваченными в различных точках пространства с помощью многопорядковых ДОЭ (матричный оптический "привод")

• •    Отклонение движения микрочастиц определенного размера от прямолинейного с помощью светового поля с поперечнопериодической структурой (оптический "сепаратор")

Слайд 33