Satellite Attitude Determination Filter using Square Root based Spherical Simplex Unscented Transformation
Автор: Kaichun Zhao, Zheng You
Журнал: International Journal of Computer Network and Information Security(IJCNIS) @ijcnis
Статья в выпуске: 4 vol.3, 2011 года.
Бесплатный доступ
A square root based spherical simplex unscented transform was adopted in micro satellite attitude determination filter. The filter computation cost was reduced evidently by means of spherical simplex unscented transformation (SSUT) and the square root technique with modified Rodrigues parameters (MRPs). The filter performance and numerical stability were guaranteed by unscented transformation with positive-semi definiteness of the state covariance propagation. The simulation results of some micro-satellite showed that this algorithm could insure accuracy, fast convergence and high robustness with high computation efficiency, which was suitable for the attitude estimation of micro-satellite.
Spheral simplex unscented transformation, quare root, scented Kalman filter, titude measurement, herical simplex
Короткий адрес: https://sciup.org/15011029
IDR: 15011029
Текст научной статьи Satellite Attitude Determination Filter using Square Root based Spherical Simplex Unscented Transformation
Published Online June 2011 in MECS
-
I. I NTRODUCTION
High precision, low computational complexity and nonlinear filter plays an essential role in attitude control system for micro satellite. Various approximate nonlinear filtering techniques have been proposed to obtain a high performance attitude measurement. Since the early 1980’s, multiplicative extended Kalman filtering algorithm (MEKF)[1] has been implemented successfully in many actual engineering application. And the algorithm has been proven to have good performance in most practical space missions where the spacecraft’s angular rate is slow and the nonlinearities are not so impactive.
In recent years, advances in space missions, such as the greater agility and lower cost demand, a variety of high efficient nonlinear filtering has been presented. Among these advanced nonlinearity filtering algorithms, only few of them are close to restrict numerical expense requirements of actual onboard implementations. More and more attention is paid to the sigma points filter (SPF) [2,3], also known as the unscented Kalman filter(UKF) in last decade. The mean and covariance of the true posteriori probability [4]
The project is supported by China Postdoctoral Science Foundation (20090460373). corresponding author: Kaichun Zhao distribution could be approximated well by means of the sigma points transform which preserves the nonlinear property of the dynamic model in the time-update phase.
Although efficient among nonlinear filters, traditional SPKF[5,6,7] still seems computational costly for engineering implementation. To further reduce the complexity, strategies for introducing fewer sigma points are exploited, known as the reduced sigma point filters. Several simplex points selection strategy have been investigated, including the n+2 point minimal-skew simplex points[8], the spherical simplex points[9] and some enhanced higher order extensions [10].
The sample point number of spherical simplex unscented transformation (SSUT) decreased from 2n+1 to n+2 for an n-dimensional state space. A new squareroot spherical simplex unscented transform was presented to improved filter performance for micro satellite attitude determination. The organization of this paper was as follows. First, we established a general 6-state stellar spacecraft attitude kinemics and measurement model, and analyzed the partially linear structure in the system. Next a square root version SSUKF estimator based on MRPs is derived in detail. Finally, we incorporated the proposed sigma point set into the attitude determination framework to configure a complete attitude estimator, and indicated its performance in simulation with comparisons to the traditional multiplicative extended Kalman filter (MEKF).
-
II. S QUARE R OOT S PHERICAL S IMPLEX U NSCENTED T RANSFORM
A.pherical Simplex Unscented Transform
The traditional Unscented Transform (UT) approximates a probability distribution of nonlinear function by symmetrically-distributed set of 2n+1 sigma points which match the mean and covariance. The computational costs of the UT are directly proportional to the number of sigma points which are used. Therefore, minimizing the number of sigma points minimizes the computational costs. The Spherical Simplex Unscented
Transformation implements this work with only n+1 sigma points for an n-dimensional space, it is proved that, these points have the same accuracy as the symmetric set, they have half the computational costs. Let χ i j be the ith sigma point in the set for jth dimensional space. It is assumed, without loss of generality, that x = 0 and P xx = I (the n x n identity matrix). The point selection algorithm for the Spherical Simplex Unscented Transformation is as follow:
-
a) Choose 0 < W 0 < 1. (1)
-
b) Choose weight sequence:
W i = (1 - W 0 )/( n + 1), i = 1,2,..., n + 1 (2)
-
c) Initialize vector sequence as:
x 0 = [ 0 ] , x 1 =[- 1/М ] , x 2 = [-, 2 W ]
Expand vector sequence for j=2,…,n according to
v j - 1
χ 0
for i = 0
j
X 1 j =i
z j - 1
- 1/ V j ( j + 1) W
j j / V j (j + 1)W1
for i = 1,
for
j
i = j + 1
B.Square-root Spherical Simplex unscented Kalman filter
The derivation of SR-UKF for nonlinear state estimation is proposed in refs [11], [12]. Similarity, the general discrete-time nonlinear system model with purely additive process and observation noise is presented as follow.
x k + 1 = F ( x k , u k ) + v k
* k = H ( x k ) + n k
Where xk is the unobserved state of the system, uk is a known exogenous input, and yk is the observed measurement signal. The process noise vk drives the dynamic system, and the observation noise is given by nk . The mappings F and H represent the deterministic process and measurement models. It is assumed that vk and nk are uncorrelated zero-mean Gaussian noise processes with covariances given by Rv and Rn .
The filter is initialized by the matrix square root of the state covariance via a Cholesky factorization. However, the propagated and updated Cholesky factor is then used in subsequent iterations to directly form the sigma points. The entire algorithm is presented as follows:
Initialization:
x = Ex 0 ], 5 0 = chol > E X x 0 - x 0 )( x 0 - x 0 ) T ]}(6)
Where E denotes expectation operator.
For k e {1,.„, да }, Calculate sigma points:
Xi , k - 1 = x k - 1 + 5 k - 1 X " , i = 0,1, L , n + 1 (7)
Time update equations:
X k\k-1 = F(X k-1, uk-1)
n + 1
x;=Z Wixkk-1
i = 0
5 k = qr {[Д( x h n + 1, kk - 1 - X - ) R i ] ]} (10)
5 k = cholupdae5 - , x 0, k\k - 1 - x - , Oa1)
y k\k-1 = H[X k\k-1](12)
n + 1
У -=Y Wiy, kk-1
i = 0
Measurement update equations:
•s * = qr {[T W i ( y„ .u k - 1 - у ;) V R n ]} (14)
5 y = cholupdate{v5 y k , y 0 , e|l _ 1 - y - , W o)} (15)
P». =!E W (X, kk-1 - X- ХУ,.4k-1- У- )T(16)
K k = (Px.J5.k T Vs*k(17)
xk = xk+K k(*k- yk)
U =K k5yk(19)
5k = cholupdate{5k-, U, -1}
III.N ONLINEAR ATTITUDE DETERMINATION FILTER STRUCTURES
A.Definition of System State Vector
The system state is defined as x. = [ q kT , b T ] , where q k and b k represents the attitude quaternion and the gyros’ bias drift term respectively. xk is combined of the global state estimate x ˆ k and a small local error state 5 xk =[ a T , A b T 1 as k kk
xk =
q k
b k
= Jf k ® 8 x k =
qk ® ба (ak) i>k+Abk
Where a k =[АФ x , АФ y , АФ z ] is the 3-axis attitude
error, A b k is the gyro drift error,
3 q ( a k ) = ^ 3 q T , 3 q 4 k J is the local error-quaternion relating to a k , and the covariance of the system is defined as:
Pk = E (3Xk3xT)
( a k - a l k )
(Abk-A b > J kk
( a k - a k ) T , ( A b k -A b k )
t ! (22)
As discussed in refs. [14], in order to guarantee stability in numerical computation process, sigma points are constructed as a scattering of local error state 3Xk , and then interpreted into a corresponding set of state points. The transform is performed by a vector of Modified Rodrigues Parameters (MRPs) 3Pk = 4 ak as a juncture [13], [14], and then л 1-13PklI2
3 q 4, k = 2 , 3 q k =
( 1 + 3 q 4, k ) 5 p k 3 q 4, k
B.System Description
The differential equations for the spacecraft’s attitude kinematics is
|
0 |
^ z |
-® y |
® x |
|
-® z |
0 |
® x |
® y |
|
® y |
-® x |
0 |
® z |
|
-® z |
-® y |
-® x |
0 |
q
Where q is the attitude quaternion referring to the inertial coordinate system, ω is the inertial angular rate vector given from the gyro’s measurement ωmeas by compensating the gyro bias b :
ю = to meas - b - n ARw (25)
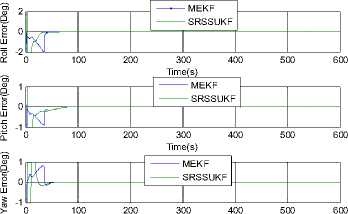
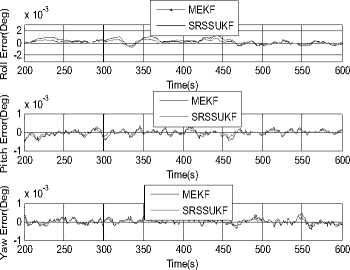
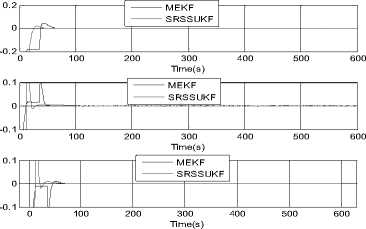
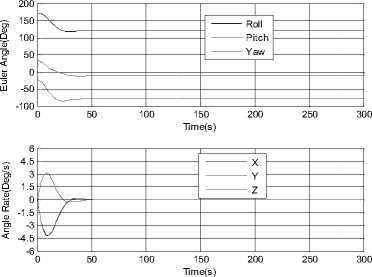
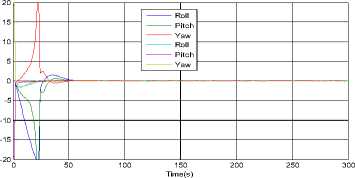
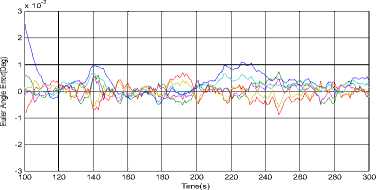
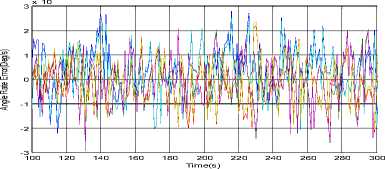
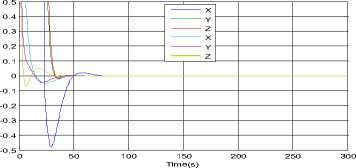
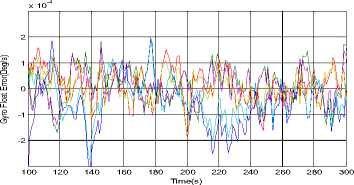
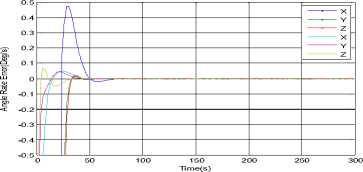
Where ηARW is a zero-mean Gaussian angular random walk noise with a covariance of modeled as a rate random walk process with white noise nRRW and a covariance of trRRW13. ^ = nRRW(26) From eqs. (24)~(26), we can derive the discrete-time version of the above models with numerical integration. /X /X/X qk / k-i = qk-i ® q^ Where qto-1 = C1 sintt -_ 2ccsjik - / 2) Ф1^! 1 -^-^cos -^-^ 1/2) 2 J T (28) with 6>k _, = meas ®и- bk-1 (29) /X /X Фk-1 = tok -1T, Фk -1 = =1 <4-11 (30) The period T is set to small enough, which is usually well satisfied in practice, and a second order accuracy is guaranteed. Not lost generality, the observation model in this article is established as an automatic star sensor with quaternion measurement qkmeas . But in actual practice this information is presented to the Kalman filter in a more convenient way as in terms of a 3-dimensional parameter. We choose to use the MRP parameter, and then the star sensor’s observation model is simply defined as the local error between the predicted and observed attitudes: zmea = h (xk) = a 3T)+Vk (31) a3T ) = 43qkT / (1 + 3q^^Г ) (32) 3qkm=qkx-i ® qm (33) Where a(3qmeas) is 3-axis attitude error relating to 3qmeas and Vk is the measurement noise covariance modeled as: Rk = ^3 (34) Clearly, such a MRPs-based expression is free from any square-root or trigonometric functions, economic in computation. The structure of attitude estimation filter is shown in figure.1. Fig.1. Structure of SRSSUKF for micro satellite attitude and rate estimation C . S p herical Simplex Unscented Kalman Filter Based on Modified Rodrigues Parameters 1) Initializaiton. Determine the set of associated weights for the sigma point: Wi, i = 1,2,..., n +1. Then initialized the global and local error state and the square root of system covariance as x0 = E[ x0 ] and S0 = chol{E[(x0 - .x0)(x0 - x0)T ]} .The system state at time step k -1 is Xk-1= [qk-, bT-1]T , the error state is 3Xk-1 = [alkT-1, AbT-1 ]T - [ 0T1,0T1 ]T and error covariance is Pk-1 . The disturbance sigma points {3x} k-1 are calculated as follows. 5Х (i) k-i = P-P • £ (i) = " s/ (i) k -i 'V b (i) k -i Sk = cholupdaeSk,SXo, kk -1-SXk, W)} (44) i = 1,2,... n + 1(35) yk / k-1 (i ) = h (X k / k-1 (i)) Where SxAb (i)k- 1 is the correction value of the n+1 yk / k-1 = ^ Wi yk / k-1 (i ) i=0 gyros’ disturbance bias drift term, Sxa (i)k-1 is the disturbance error of axis angular parameter. The disturbance error quaternion for Sxa (i)k-1 is as follows. 3) Measurement update. We have the innovation Then the innovation covariance is calculated as S.k = qr{[VW:(yto.1,kk-1 -y-) VRv]} (47) sq (sx (i)k_1)= 8-X (i)k-1 |6 sX (i)k-1SX (i)kJ 16+(sX (i)T-1^X (i)k-1) The sigma points { χ}k-1 are calculated with compounding disturbance sample points Sxa (i)k-1 and reference state Xk 1 = [qT-1, bT1 ]T . The revised sigma points are as follows: X(0)k-1 = xk-1 = ˆ qk-1 ˆ -1 bk X(i)k-1 = xk-1 ®sx0)k-1 Syk = cholupdate{sSyk, Уо,kk-1 - yk, Wo)} (48) n+1 Px.,. =^W (Sx, kk-1 -sx- )(yi,kk-1 - y- )T (49) i=0 ^xk = ^xk+ K k(,k- yk) U = K kSyk(51) Sk = cholupdate{S-, U, -1} 4) State update and error state reset. sqk =T(i+sq4, k)sPT, sq 4, k IT sq4, k =(i - IsPklГ )/(i+| Sp. I2) qk-1 ®Sq (sX(i)k-1) . bk-1s(i)k-1 . , г =1,..., n+1. xk = qˆk bk qk / k-1 ® sqk . bk / k-1+Abk sX:k = [ 0T1,03Tx1]T (55) 2) Time propagation. In this process, the global state xk । is propagated with Eqs. (24), (25) by numerical integration to Xk/k-1 , and each of the sigma point, x (i) is also propagated with Eqs. (24), (25) to xk/k-1 (i). Then the updated disturbing sigma point could be abstracted from Xk/k । (i): sX k-1 (i ) = xk/1k-1 ® X k / k-1 (i) = q k/k-1 ® X k / k-1(i) Xbbm-i( i)- hik-v k / k -1 k / k -1 sPk / k-1 (i) = SQk / k-1 (i )/(l+Sq 4 k / k-1 (i)) xk / k-1 (i ) = [ qT' k-1 (i ), A bk' k-1 (i )] T (41) = [4SPk/k-1 (i), AbT'k-1 (i)] In the same time, the observation estimation is calculated with Eqs. (31) ~ (33) as The predicted mean error state, mean observation and covariance is given respectively by sX k / k-1 =£ WiSxk / k-1 (i) (42) i=0 S--= qr{[^. (SX1n.Uk-1-SX-) Rv]]} (43) IV.SIMULATION In order to validate the effectiveness of the proposed algorithm simulation is performed by attitude determination system of some satellite. A multiplicative Extended Kalman filter is also simulated as a comparison, with its initial state and all other parameters equivalent. The spacecraft’s 3-axis inertia is [58.4, 51.2, 28.0]( kg • m2 ); The precision and sampling period of the sensors are: Gyro scopes nARw = 0.01o / 4h, Hrrw = 5o / h(100 5), dt = 0.055 . The star sensor is simulated with 3σ accuracy as: cross boresight 7 arc-seconds; around boresight 35 arc-seconds, and the sensor’s update-rate is 5Hz. The filtering period is set to be 0.05s, which is the equal to the sampling speed of gyro scopes. In scenario one, the spacecraft was controlled from an initial attitude [36.1 °,40.0 °,29.9 °], angular rate [0.80 ° /s,0.90 °s,0.7 °s]to near zero, and kept in 3-axis stability. Figure 2a illustrated the history of 3-axes Euler angle estimation and attitude error of the two filters. As can be seen, the multiplicative SRSSUKF presented a significantly better convergence speed. In the transitional process, the multiplicative SRSSUKF was smoother than the multiplicative EKF. The attitude measurement precision of the two filters is almost equivalent after the micro satellite attitude comes to stabilization. The angular rate estimation was performed with fig.3. From fig.3a, we can see the convergence time with SRSSUKF is about 1/2 of the one with MEKF. And the 3 axis angular rate measurement precision with in ± 0.0002 7s (3σ accuracy ) be achieved by both filters. Time(s) Fig.2a. History of attitude angle error of the spacecraft of SRSSUKF and MEKF Fig.2b. Euler angle error of the spacecraft with SRSSUKF and MEKF when the spacecraft attitude estimation is with stable state Fig.3a. History of angular rate error of the spacecraft with SRSSUKF and MEKF MEKF -2 200 250 300 350 400 450 500 550 600 x 10-4 200 250 300 -2 Time(s) 350 400 450 500 550 600 Time(s) -2 200 250 300 350 400 450 500 550 600 Time(s) Fig.3b. Angular rate error of the spacecraft with SRSSUKF and MEKF when the spacecraft attitude estimation is with stable state In scenario two, the spacecraft was implemented rapid maneuver with high speed sinusoid angle rate movement from an initial attitude [171.8 7 32.4 7 -23.3 7, angular rate [0.0001 7s, 0.0004 7s, 0.0002 7s]. The control object attitude and angular rate is with [121.0 ° 12.1 ° -78.4 ° ] and [0 7s, 0 7s, 0 7s]. And the spacecraft movement of attitude and angular rate is indicated in Fig.4. The angular rate is increased from 0 7s to about 4 7s , and then decreased from maximum to 0 7s in one minute during spacecraft rapid big attitude angular maneuver. Fig.4. The big attitude angle and rate movement of some satellite maneuver Fig.5 showed the history of attitude angle error of the spacecraft with the two filters. The real line is with square root SSUKF and the dashed one is with MEKF. From fig.5 a, we can clear see that the multiplicative SRSSUKF presented a much faster convergence velocity than the multiplicative EKF. And the attitude estimation precision of multiplicative SRSSUKF is a little better than MEKF when the spacecraft attitude estimation come to stable state (shown in Fig.5 b). Fig.5a. History of attitude angle error of the spacecraft with SRSSUKF and MEKF Fig.5b. Attitude angle error of the spacecraft with SRSSUKF and MEKF when the spacecraft attitude estimation is with stable state with SRSSUKF and MEKF Fig.7b. Angular rate error of the spacecraft with SRSSUKF and MEKF when the spacecraft attitude estimation come to stable state Fig.6 showed the history of gyro float error of the spacecraft with the two filters. The legend of two filters is same as fig.5. From fig.6 a, we can easily see that the multiplicative SRSSUKF presented a much shorter convergence time than the multiplicative EKF. And the gyro float estimation precision of multiplicative SRSSUKF is a little better than the one of MEKF when the spacecraft attitude estimation come to stable state (shown in Fig.6 b). Fig.6a. History of gyro float error of the spacecraft with SRSSUKF and MEKF Fig.6b. Gyro float error of the spacecraft with SRSSUKF and MEKF when the spacecraft attitude estimation come to stable state Fig.7 showed the history of angular rate error of the spacecraft with the two filters. The legend of two filters is same as the above figures. From fig.7 a, we can clear see that the multiplicative SRSSUKF presented a much faster convergence velocity than the multiplicative EKF. And the angular rate estimation precision of multiplicative SRSSUKF is equivalent to the one of MEKF when the spacecraft attitude estimation come to stable state (shown in Fig.7 b). Fig.7a. History of angular rate error of the spacecraft V. CONCLUSION A square root version of the SSUKF for spacecraft attitude and angular rate estimation has been presented and tested through simulation. Some essence technique has been developed within computation affordability consideration. The simulation results validated the effectiveness of the proposed algorithm, and concluded in that the multiplicative SRSSUKF had a better precision and a faster convergence speed than its traditional counterpart multiplicative EKF. ACKNOWLEDGMENT The authors would like to thank Dr. Fan Chunshi and Dr. Meng Ziyang for their fruitful theory and engineering discussion on micro satellite attitude measurement and control.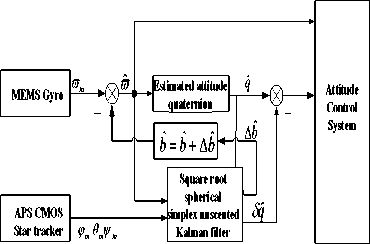


Список литературы Satellite Attitude Determination Filter using Square Root based Spherical Simplex Unscented Transformation
- E. J. Lefferts, F. L. Markley, M. D. Shuster, Kalman Filtering for Spacecraft Attitude Estimation, Journal of. Guidance, Control and Dynamics,1982,5(5):417-429.
- S. J. Julier and J. K. Uhlmann, “Unscented filtering and nonlinear estimation,” Proc. IEEE, vol. 92, pp. 401–422, Mar. 2004.
- R. van der Merwe and E. A. Wan, “Sigma-point Kalman filters for nonlinear estimation and sensor-fusion-applications to integrated navigation”, AIAA Guidance, Navigation, and Control Conference, v3, p 1735-1764, 2004.
- S. J. Julier and J. K. Uhlmann, and H. Durrant-Whyte, “A new approach for filtering nonlinear systems,” Proceedings of the American Control Conference, pp. 1628–1632, 1995.
- Julier S J, Uhlmann J K, Durrant-Whytte H F. A new method for the nonlinear transformation of means and covariance in filter and estimators. IEEE Transactions on automatic control, 2000,45(3):477-482.
- Merwe R V, Doucet A, Freitas N De. The Unscented Particle Filter. Technical Report CUED/F-INPENG/TR 380, Cambridge University Engineering Department,2000
- Julier S J, Uhlmann J K. Reduced sigma point filters for the propagation of means and covariances though nonlinear transformations. Proceeding of the American Control Conference.Anchorage AK,2002.
- Julier S J. The spherical simplex unscented transformation[A]. Proceeding of the American Control Conference.Denver, Colorado,2003.
- Chunshi Fan, Zheng You.Highly Efficient Sigma Point Filter for Spacecraft Attitude and Rate Estimation. Mathematical Problems in Engineering.Volume 2009 (2009), Article ID 507370, 23 pages.
- J. Levesque, “Second-Order Simplex Sigma Points for Nonlinear Estimation”, AIAA Guidance, Navigation and Control Conference and Exhibit.2006.
- R. van der Merwe, E.A. Wan, Square-root unscented Kalman filter for state and parameter estimation, in: Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Proces- sing, Salt Lake City, UT, May 2001, 3461–3464.
- Xiaojun Tang, JieYan, DuduZhong. Square-root sigma-point Kalman filtering for spacecraft relative navigation. Acta Astronautica 66 (2010) 704-713.
- Shuster, M.D., ” A survey of attitude representations”. Journal of the Astronautical Sciences, 41(4), 439-517(1993).
- Crassidis, J.L., ”Sigma-point Kalman filtering for Integrated GPS and Inertial Navigation”, IEEE Transactions on Aerospace and Electronic Systems, 42(2), 750-756(2006).


