Сборные сферические оболочки из шестиугольных панелей

Автор: Антошкин В.Д., Коновалов А.Г.

Статья в выпуске: 13 т.3, 2015 года.

Бесплатный доступ

Рассмотрены вопросы конструктивно-технологического формообразования сферических оболочек на основе геодезической сети. Исследовано несколько конструктивно-технологических методов образования треугольных сетей на сфере, которые были названы «Транер». В каждой из них критерием оптимальности является минимальное число типоразмеров конструктивных деталей и минимальное число монтажных элементов купола, возможности укрупнительной сборки и предварительного напряжения.

Конструктивно-технологическая форма, купол, панель, правильный шестиугольник, разрезка, сборная сферическая оболочка

Короткий адрес: https://sciup.org/147248891

IDR: 147248891

Текст научной статьи Сборные сферические оболочки из шестиугольных панелей

Во всех конструктивных решениях куполов просматривается тенденция применения уже на стадии разрезки и формообразования этих покрытий эффективных технологических решений изготовления отдельных элементов, стендовой укрупнительной сборки сегментов куполов, возведения их с обеспечением заданной точности монтажа покрытия, в целом, или основных его несущих конструкций. Учитывая, что не все возможности разбиения сферы на панели или стержни еще исчерпаны и то, что преобладающее количество сетчатых куполов построено на сфере, проанализируем решения сборных сферических куполов из шестиугольных панелей, исходя из построений на сфере треугольной сети [1; 2].

Оптимизация треугольной геометрической сети на сфере по критерию минимума типоразмеров элементов может быть представлена и решена размещением правильных и неправильных шестиугольников, вписанных в окружности минимальных размеров, например, в сферических секторах, показанных на рисунках 1 и 2. Кроме перечисленных вариантов применения свойств симметрии главных линий-окружностей сферы, в подобных 1

разрезках должны быть реализованы возможности центральной симметрии окружностей. Использование указанных окружностей для построения геометрической сети из треугольников и шестиугольников позволяет на 5-30% снизить число типоразмеров монтажных элементов купола, получить при необходимости плоские шестиугольные панели, а также воспользоваться конструктивными преимуществами предварительного напряжения.

Нами предложены и исследованы несколько конструктивно-технологических методов образования треугольных сетей на сфере с шестиугольными монтажными панелями, которые названы системой «Транер» [3; 4]. В каждой из них критерием оптимальности является минимальное число типоразмеров конструктивных деталей и минимальное число монтажных элементов купола, возможности укрупнительной сборки и предварительного напряжения.

Суть предложенных вариантов разрезок «Транер» заключается в том, что сборная сферическая оболочка составляется из монтажных шестиугольных панелей, разнотипные марки которых одинаковым образом полностью или частично расположены в пределах секторов, имеющих общую вершину сферы на панели, выполненной в виде правильного шестиугольника. Панели в виде правильных и неправильных шестиугольников могут иметь убывающие размеры от центральной панели к периферии. Но панели в виде правильных шестиугольников могут иметь и одинаковые размеры панелей, расположенных по границам секторов, которые являются осями симметрии сферы.

Для первого варианта решений в пределах секторов, составляющих 60°, в сборных сферических оболочках шестиугольные панели выполнены с углами, описанными окружностями со своими радиусами из центров панелей, лежащих на сфере. Между шестиугольными панелями расположены треугольные панели (несущие или ненесущие); углы шестиугольных панелей описаны своими радиусами из центров панелей, смежные шестиугольные панели соединены между собой в точках пересечения и в точках касания окружностей, описывающих панели. Панели, смежные с шестиугольной панелью на вершине купола, выполнены одного радиуса и также в виде правильных шестиугольников. Шестиугольные панели могут быть выполнены также в свою очередь из треугольных панелей с узлом соединения в центре шестиугольной панели (центре окружности, в которую они вписаны). На рисунках 1 (а) и (б) изображен, соответственно, вид сверху и сбоку сборной сферической оболочки с шестью секторами в плане, составляющими 60°.

Во втором варианте для секторов, составляющих 120°, на вершине сферы расположена панель, выполненная в виде правильного треугольника, а смежные с центральной треугольной панелью правильные шестиугольные панели вписаны в окружности одного радиуса. Панели с центрами, расположенными по границам секторов, 2

выполнены в виде правильных шестиугольников либо с одинаковыми, либо с убывающими

от вершины к периферии радиусами.

а)

б)

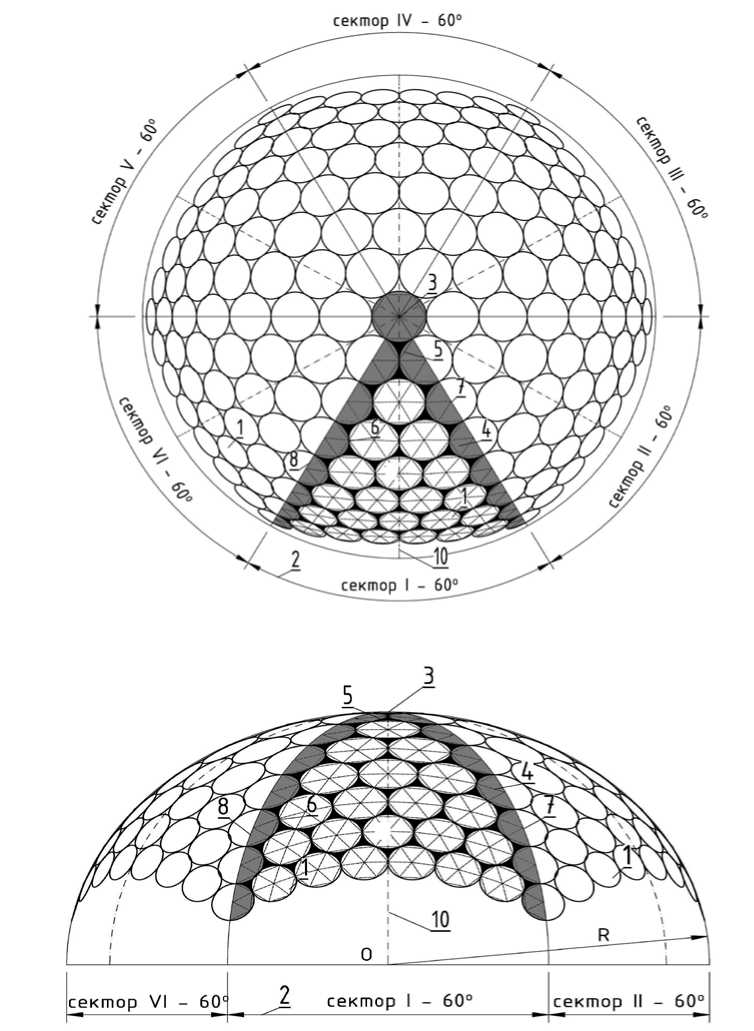
Рис. 1. Схема сборной сферической оболочки из 6 секторов с углами на вершине 60° с разрезкой из шестиугольных панелей с треугольными вставками между ними: а – вид сверху; б – вид сбоку; 1 – панели в виде плоских шестиугольников; 2 – сектора; 3 – панель на вершине купола в виде правильного плоского шестиугольника;

4 – панели в виде правильных шестиугольных панелей (выделены серым цветом);

5 – панели в виде треугольника; 6 – узлы соединения шестиугольных панелей;

7 – центры шестиугольных панелей; 8 – границы секторов;

9 – остаточная треугольная панель; 10 – ось сектора

На рисунке 2 (а) показан вид сверху сборной сферической оболочки с тремя секторами в плане, составляющими 120°; на рисунке 2 (б) – вид сбоку сборной сферической оболочки с тремя секторами в плане, составляющими 120°.

а)

б)

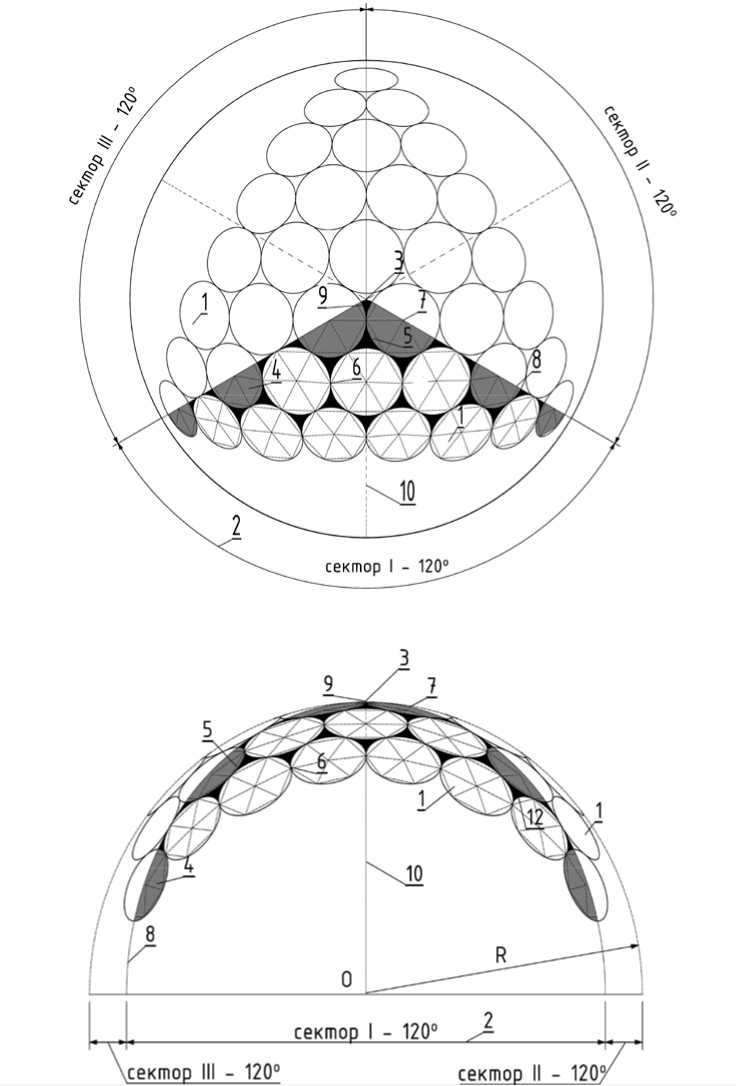
Рис. 2. Схема сборной сферической оболочки из 3-х секторов с углами на вершине 120° с разрезкой из шестиугольных панелей с треугольными вставками между ними: а – вид сверху; б – вид сбоку; 1 – панели в виде плоских шестиугольников; 2 – сектора;

3 – панель на вершине купола в виде правильного плоского треугольника; 4 – панели в виде правильных шестиугольных панелей (выделены серым цветом); 5 – панели в виде треугольника; 6 – узлы соединения шестиугольных панелей; 7 – центры шестиугольных панелей; 8 – границы секторов;

9 – остаточная треугольная панель; 10 – ось сектора.

На рисунке 3 показаны схемы распределения окружностей, описывающих шестиугольники, в сегментах 90 ÷ 90–2r и 90+r ÷ 90+r–2r относительно линии экватора 2 сферы и относительно главной окружности «зенит-надир».

Распределение окружностей на сфере по данным схемам представляет теоретическую основу размещения максимального числа окружностей одного радиуса с учетом касания попарно трех смежных окружностей и образования между ними треугольника. На схемах рисунка 3 показано, как с помощью этих сегментов можно разместить окружности в секторе под наклоном 60о к экватору или под наклоном 30о к экватору.

Зкватор

Главная окружност nod углом 30° к экватору

Г лобная окружность/ // nod углом 90° - к экватору

Рис. 3. Схемы распределения окружностей, описывающих шестиугольники.

При разработке алгоритма геометрического расчета разрезок, предлагаемых конструктивно-технологических систем, воспользуемся также повторяемостью параметров сети на любом сферическом треугольнике и, соответственно, на любом совместимом сферическом треугольнике или в сферическом секторе. При решении указанной проблемы предложены автоматизированные средства в системах AutoCAD и LIRA 9.4, дополненные специальными программными элементами.

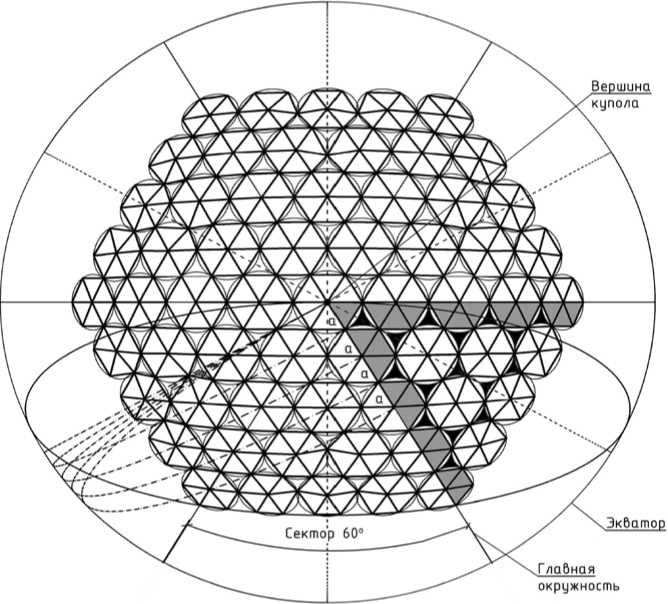
Для применения методов расчета с помощью сферической тригонометрии воспользуемся зависимостями на плоскости диаметра окружности сферы, вписанных в них многоугольников и радиусов. С учетом ограничений, которые дают разрезки на основе секторов 60о, получаем оптимальную по критерию минимума типоразмеров разрезку на сфере с пятью рядами окружностей (см. рис. 4), состоящую из монтажных только 5

шестиугольных панелей девяти типоразмеров или из пяти правильных шестиугольных панелей, четырех неправильных шестиугольных панелей и двенадцати треугольных панелей-вставок (для стержней – всего 33-х типоразмеров).

а)

б)

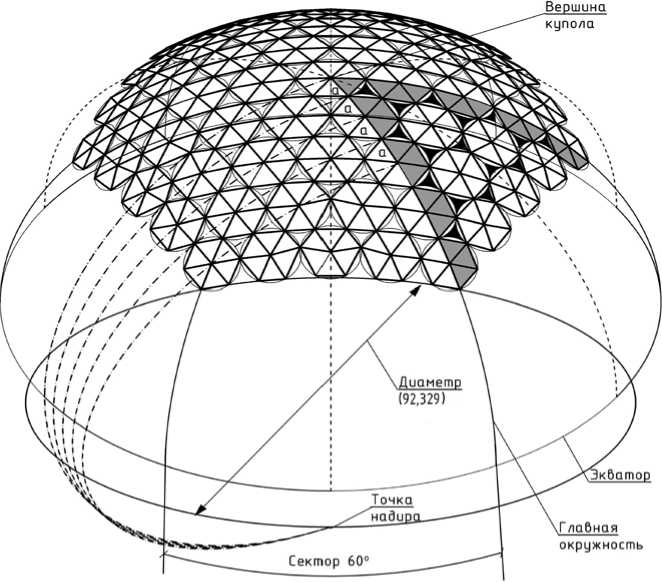
Рис. 4. Схема сборной сферической оболочки диаметром 100 м (60 м между опорами) из 6 секторов с углами на вершине 60° с разрезкой из шестиугольных панелей с треугольными вставками между ними.

Опорный контур сборной оболочки выполняется в виде шести арок радиусом 46,1645 м (рис. 4б), выполненных по окружностям, проходящим через точку «надир» и углы опорных шестиугольных панелей. Координаты оболочки (рис. 4а, б) диаметром 100 м наиболее эффективной разрезки приведены в таблице 1.

Таблица 1

Координаты узлов части сетчатого купола для диаметра 100 м

№ узла	X (м)	Y (м)	Z (м)	№ узла	X (м)	Y (м)	Z (м)
1	2	3	4	5	6	7	8
1	0	0	0	37	-13.3222118	7.691582438	-2.42523535
2	-4.53831182	-2.620195575	-0.27537524	38	-17.5121127	5.05923327	-3.44111178
3	0.000000061	-5.240391054	-0.27537516	39	-17.5603732	-0.00000007	-3.1851166
4	4.538311829	-2.620195554	-0.2753753	40	-17.5121127	-5.059233452	-3.44111164
5	4.538311814	2.620195565	-0.27537537	41	-17.4164916	-10.05541621	-4.22277363
6	-1.25E-08	5.2403911	-0.27537538	42	-13.1374809	-12.63631789	-3.44111156
7	-4.53831183	2.620195544	-0.27537531	43	-8.78018653	-15.20772931	-3.18511645
8	-8.97904907	-0.000000007	-0.81284025	44	-4.37463168	-17.69555122	-3.44111156
9	-8.97865142	-5.183826871	-1.08669126	45	0.000000078	-20.11083224	-4.22277362
10	-4.48952453	-7.776084615	-0.81284017	46	4.374631753	-17.69555118	-3.44111163
11	0.000000009	-10.36765366	-1.08669126	47	8.780186597	-15.20772925	-3.18511659
12	4.489524525	-7.77608461	-0.81284024	48	13.13748097	-12.6363178	-3.44111176
13	8.978651435	-5.183826824	-1.0866914	49	17.41649156	-10.05541609	-4.22277389
14	8.979049062	-1.55E-08	-0.81284038	50	17.51211268	-5.05923336	-3.4411119
15	8.978651426	5.183826803	-1.08669154	51	17.56037311	-1.35E-08	-3.18511686
16	4.489524543	7.77608457	-0.81284045	52	17.51211265	5.059233361	-3.44111204
17	-2.95E-08	10.36765362	-1.08669154	53	17.41649149	10.05541609	-4.22277417
18	-4.4895246	7.776084549	-0.81284039	54	13.13748092	12.63631775	-3.44111211
19	-8.97865147	5.183826758	-1.08669141	55	8.780186541	15.20772918	-3.185117
20	-13.370999	2.535693466	-1.88777027	56	4.374631688	17.6955511	-3.44111211
21	-13.370999	-2.535693585	-1.8877702	57	-9.9E-08	20.11083212	-4.22277418
22	-13.3222117	-7.69158262	-2.42523514	58	-4.37463183	17.69555108	-3.44111205
23	-8.88147449	-10.31177814	-1.88777013	59	-8.78018667	15.20772914	-3.18511688
24	-4.48952446	-12.84747165	-1.88777012	60	-13.137481	12.63631768	-3.44111192
25	6.75E-08	-15.38316512	-2.42523513	61	-17.4164916	10.05541594	-4.22277391
26	4.489524526	-12.84747161	-1.88777019	62	-21.5172829	7.371619292	-5.47286476
27	8.881474537	-10.31177808	-1.88777026	63	-21.6181481	2.438710267	-4.98102203
28	13.32221177	-7.691582532	-2.42523534	64	-21.6181481	-2.438710512	-4.98102196
29	13.37099902	-2.535693516	-1.8877704	65	-21.5172828	-7.37161955	-5.47286456
30	13.37099901	2.535693535	-1.88777047	66	-21.332552	-12.31635481	-6.48874098
31	13.32221174	7.691582506	-2.42523555	67	-17.1426511	-14.94870399	-5.47286449
32	8.881474499	10.31177805	-1.88777054	68	-12.9210591	-17.50251034	-4.98102182
33	4.489524478	12.84747157	-1.88777054	69	-8.69708883	-19.94122071	-4.98102182
34	-4.55E-08	15.38316505	-2.42523555	70	-4.37463167	-22.32032335	-5.47286448
35	-4.48952457	12.84747155	-1.88777048	71	-7E-09	-24.63270939	-6.48874097
36	-8.88147458	10.31177801	-1.88777041	72	4.374631743	-22.32032332	-5.47286454

Продолжение таблицы 1

1	2	3	4	5	6	7	8
73	8.697088896	-19.94122065	-4.98102195	117	16.82465476	19.5639341	-7.17263217
74	12.92105919	-17.50251025	-4.98102201	118	12.23980157	21.1999582	-6.40241989
75	17.14265109	-14.94870387	-5.47286474	119	8.530536508	24.35254549	-7.17263217
76	21.33255201	-12.31635467	-6.4887413	120	4.215500941	26.62389155	-7.88826873
77	21.5172828	-7.371619436	-5.47286488	121	-1.26E-07	28.75164615	-9.09348702
78	21.61814803	-2.438710398	-4.98102228	122	-4.2155012	26.62389153	-7.88826867
79	21.61814802	2.438710382	-4.98102235	123	-8.53053674	24.35254545	-7.17263205
80	21.51728276	7.371619405	-5.47286508	124	-12.2398017	21.19995815	-6.40241971
81	21.33255192	12.31635464	-6.48874164	125	-16.824655	19.56393401	-7.17263192
82	17.14265104	14.94870377	-5.47286515	126	-20.9492161	16.96267661	-7.88826841
83	12.92105913	17.50251015	-4.98102249	127	-24.8996562	14.37582288	-9.09348664
84	8.697088823	19.94122054	-4.98102249	128	-28.6135461	11.65239699	-10.6873223
85	4.374631661	22.32032318	-5.47286516	129	-28.9564318	6.864892504	-9.82042409
86	-1.31E-07	24.63270921	-6.48874165	130	-29.0278167	2.331750701	-9.35582679
87	-4.37463186	22.32032316	-5.4728651	131	-29.0278167	-2.331751103	-9.35582672
88	-8.697089	19.94122049	-4.98102237	132	-28.9564318	-6.864892919	-9.8204239
89	-12.9210593	17.50251008	-4.9810223	133	-28.6135461	-11.65239743	-10.687322
90	-17.1426512	14.94870368	-5.4728649	134	-28.2302101	-16.29871962	-12.086849
91	-21.3325521	12.31635444	-6.48874132	135	-24.398045	-18.95385942	-10.6873219
92	-25.1647171	9.661214679	-7.88826828	136	-20.4233873	-21.64455934	-9.82042376
93	-25.3551915	4.78861124	-7.17263165	137	-16.5332638	-23.97295135	-9.35582652
94	-24.4796033	-1.275E-07	-6.40241932	138	-12.4945527	-26.30470223	-9.35582652
95	-25.3551915	-4.788611564	-7.17263152	139	-8.53304432	-28.509452	-9.82042375
96	-25.1647171	-9.661215022	-7.88826801	140	-4.21550096	-30.60625654	-10.6873219
97	-24.8996561	-14.37582336	-9.09348624	141	9.05E-08	-32.59743889	-12.0868489
98	-20.949216	-16.96267701	-7.88826794	142	4.215501022	-30.60625651	-10.687322
99	-16.8246548	-19.56393436	-7.17263138	143	8.533044376	-28.50945194	-9.82042388
100	-12.2398016	-21.19995842	-6.40241912	144	12.49455278	-26.30470215	-9.3558267
101	-8.53053653	-24.35254573	-7.17263137	145	16.53326381	-23.97295123	-9.35582677
102	-4.21550097	-26.62389179	-7.88826793	146	20.42338732	-21.6445592	-9.82042407
103	-2.15E-08	-28.75164641	-9.09348623	147	24.39804499	-18.95385925	-10.6873223
104	4.215501038	-26.62389176	-7.88826799	148	28.23020997	-16.29871947	-12.0868494
105	8.530536597	-24.35254567	-7.1726315	149	28.61354599	-11.65239727	-10.6873224
106	12.23980165	-21.19995834	-6.4024193	150	28.95643166	-6.864892764	-9.82042433
107	16.82465483	-19.56393424	-7.17263163	151	29.02781654	-2.331750948	-9.35582716
108	20.949216	-16.96267687	-7.88826825	152	29.02781653	2.331750856	-9.35582722
109	24.89965604	-14.37582322	-9.09348662	153	28.95643162	6.864892659	-9.82042452
110	25.16471701	-9.661214888	-7.88826839	154	28.61354593	11.65239714	-10.6873227
111	25.35519138	-4.788611429	-7.1726319	155	28.23020994	16.29871919	-12.0868498
112	24.4796032	-0.000000041	-6.40241969	156	24.39804492	18.95385903	-10.6873228
113	25.35519135	4.788611375	-7.17263203	157	20.42338724	21.644559	-9.82042466
114	25.16471695	9.661214813	-7.88826865	158	16.53326372	23.97295103	-9.35582742
115	24.89965596	14.37582311	-9.09348701	159	12.49455269	26.30470193	-9.35582742
116	20.94921593	16.96267672	-7.88826872	160	8.533044273	28.50945169	-9.82042466

С учетом ограничений, которые дают разрезки на основе секторов 120о, получаем оптимальную по критерию минимума типоразмеров разрезку на сфере с тремя рядами окружностей (см. рис. 5), состоящую из монтажных только шестиугольных панелей четырех типоразмеров или из правильной шестиугольной панели, одной неправильной шестиугольной панели того же радиуса, двух неправильных шестиугольных панелей разных радиусов и семнадцати треугольных панелей-вставок (для стержней – всего 15-ти типоразмеров).

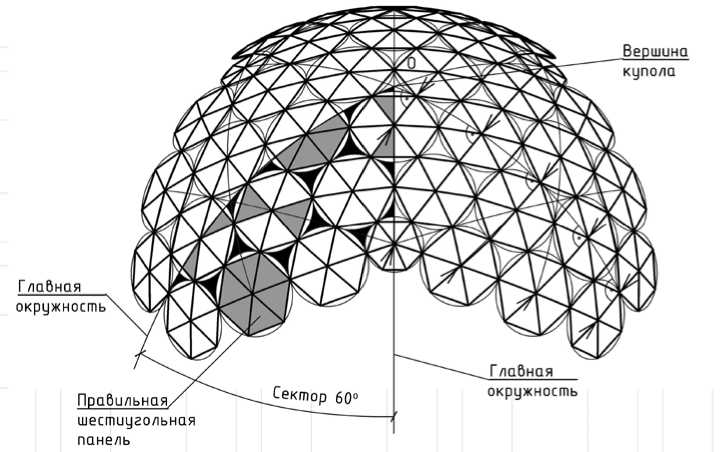
Рис. 5. Схема сборной сферической оболочки диаметром 50 м (36 м между опорами) из 3 секторов с углами на вершине 120° с разрезкой из шестиугольных панелей с треугольными вставками между ними.

Опорный контур сборной оболочки выполняется разомкнутым с использованием под входы участки нестандартных панелей малого радиуса, выполненных также по главным окружностям сферы и проходящим через углы опорных шестиугольных панелей. Координаты оболочки диаметром 50 м наиболее эффективной разрезки для секторов 120о (рис. 5) приведены в таблице 2.

На основе анализа систем разбиения сферы в пределах секторов составлены базовые сферические структуры, которые предоставляют следующие три системы разбивки оболочки:

• одноконтурная система из плоских или пространственных шестиугольников с

треугольниками между ними (система «Т60» – рисунки 1, 2, 4);

• одноконтурная система из плоских или пространственных шестиугольников с

треугольниками между ними (система «Т120» – рисунок 5);

• двухконтурная система, состоящая из шестигранных пирамид, вершины которых соединены стержнями (система «Т60ПС» – рисунок 1, 2, 4).

Системы разрезок показанного способа образования треугольных, шестиугольных сетей обозначены цифровыми и буквенными индексами.

Таблица 2

Координаты узлов основной части сетчатого купола для диаметра 50 м

№ узла	X (м)	Y (м)	Z (м)	№ узла	X (м)	Y (м)	Z (м)
1	2	3	4	5	6	7	8
1	-4.8E-06	1.129298	0.051117	26	3.862713	-2.23014	0.822846
2	-0.97803	-0.56461	0.051117	27	4.793107	-0.50876	0.966688
3	0.977975	-0.56469	0.051117	28	5.553313	1.105354	1.355992
4	1.95595	1.129269	0.205733	29	4.628173	2.672078	1.199999
5	0.977975	2.822938	0.362266	30	3.733919	4.256635	1.355992
6	-0.97798	2.822937	0.362266	31	2.885686	5.80767	1.813851
7	-1.95595	1.129268	0.205733	32	0.977974	5.987732	1.57111
8	-2.93372	-0.56452	0.362266	33	-0.97798	5.987732	1.57111
9	-1.95575	-2.25842	0.362266	34	-2.88569	5.807669	1.813851
10	0	-2.25854	0.205733	35	-3.73392	4.256633	1.355992
11	1.955748	-2.25842	0.362266	36	-4.62817	2.672076	1.199999
12	2.933723	-0.56452	0.362266	37	-5.55331	1.105352	1.355992
13	3.863663	1.101419	0.663236	38	-6.47243	-0.40476	1.813851
14	2.885687	2.795322	0.663236	39	-5.67452	-2.14691	1.57111
15	1.95595	4.405335	0.966688	40	-4.69654	-3.84082	1.57111
16	-7.4E-07	4.460277	0.822846	41	-3.58675	-5.40291	1.813851
17	-1.95595	4.405334	0.966688	42	-1.81939	-5.36199	1.355992
18	-2.88569	2.795321	0.663236	43	0	-5.34415	1.199999
19	-3.86366	1.101418	0.663236	44	1.819393	-5.36199	1.355992
20	-4.79311	-0.50876	0.966688	45	3.586745	-5.40291	1.813851
21	-3.86271	-2.23014	0.822846	46	4.696541	-3.84082	1.57111
22	-2.83716	-3.89657	0.966688	47	5.674515	-2.14691	1.57111
23	-0.97798	-3.89674	0.663236	48	6.472433	-0.40475	1.813851
24	0.977975	-3.89674	0.663236	49	7.113329	1.237273	2.296093
25	-4.8E-06	1.129298	0.051117	50	3.862713	-2.23014	0.822846

Системы «Т60» и «Т120» – это такая разбивка, которая позволяет собирать купол из плоских (складчатых, сферических) треугольных и шестиугольных панелей на основе секторов с углом при вершине 60о (см. рис. 1, 2, 4).

Разрезки способа «Т60ПС» дают возможность собирать двухпоясной (двухуровневый) купол такой же разрезки, что и у однопоясных куполов «Т60», но из шестиугольных пирамидальных стержневых панелей, а разрезки «Т60ПП» – из двухпоясных пространственных элементов (см. рис. 6, 7).

Таблицы 1 и 2 координат сборной сферической оболочки диаметром 100 м (60 м между опорами) из 6 секторов с углами на вершине 60° с разрезкой из шестиугольных панелей, а также сборной сферической оболочки диаметром 50 м (36м между опорами) из 3 секторов с углами на вершине 120° с разрезкой из шестиугольных панелей позволяют вычертить основные архитектурно-строительные чертежи покрытия здания, монтажные схемы и их фрагменты в любом ракурсе, выполнить конструирование купола, а также все статические и динамические расчеты.

а)

б)

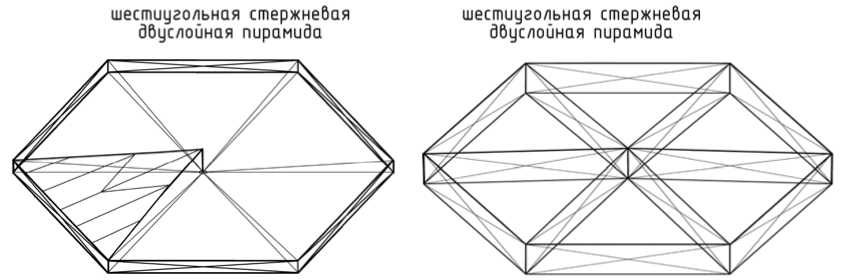
Рис. 6. Пирамидальные стержневые панели сборной сферической оболочки: а – предварительно-напряженная шестиугольная двухуровневая панель; б – металлодеревянная шестиугольная двухуровневая панель.

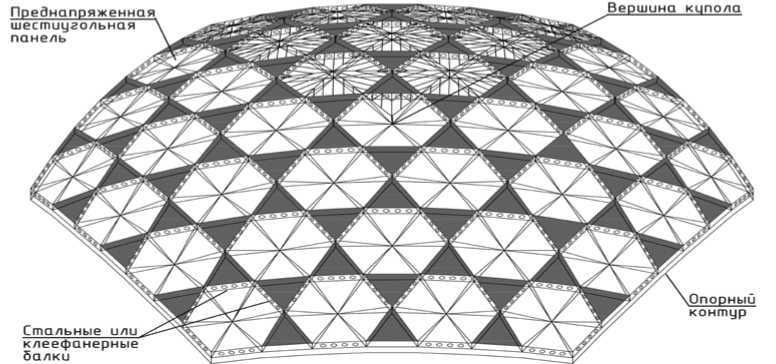
Рис. 7. Схема двухуровневой (двухслойной) разрезки сборной сферической оболочки способом «Т60ПС».

На рисунке 8 приведен пример спроектированного светопрозрачного купольного покрытия стадиона и продемонстрирована методика определения размеров сборных деталей и монтажных схем с помощью таблицы 1 координат. По приведенным рисункам и схемам можно получить визуальное представление о специфических композиционных и строительных различиях существующих геодезических оболочек и предлагаемых конструктивно-технологических форм сферических оболочек, имеющих эффективные геометрические основы.

Рис. 8. Запроектированное сборное сферическое покрытие хоккейного стадиона «Айсберг» пролетом 120 м на основе секторной разрезки «П60 ПС».

Разработанные сборные сферические оболочки системы «Транер» могут применяться для покрытий зданий различного назначения, а также для устройства сферических отражателей в зеркальных антеннах и концентраторах энергии. По сравнению с аналогами, эти оболочки имеют максимум однотипных монтажных элементов, возможности укрупнительной сборки и максимум эстетического качества при минимуме сборных деталей.

Список литературы Сборные сферические оболочки из шестиугольных панелей

Павлов Г. Н. Композиционное формообразование кристаллических куполов и оболочек//Архитектура СССР. -1977. -№ 7. -С. 30-41.
Туполев М. С. Геометрия сборных сферических куполов//Архитектура СССР. -1969. -№ 1. -С. 35-41.
Травуш В. И., Антошкин В. Д., Ерофеев В. Т. Сборная сферическая оболочка. Патент на полезную модель № 129534 от 27.06.13 г. EDN: DFUNWC
Травуш В. И., Антошкин В. Д., Ерофеев В. Т. Сборная сферическая оболочка. Заявка на изобретение RU № 2012116363 от 20.02.14 г. EDN: HACXHP

Статья научная