Сценарное прогнозирование деградации информационно-вычислительных ресурсов подвижного объекта

Вопросы методологии проектирования и построения бортовых вычислительных комплексов подвижных объектов (далее – БВК ПО) с перестраиваемой структурой, компенсирующей возмущающие факторы, и управления производительностью деградирующей вычислительной структуры не теряют своей актуальности.

Известные исследования относятся прежде всего к априорным вариантам парирования отказов и сбоев на основе тривиальных схем резервирования – мажоритированию на уровне каналов, задействованию ненагруженного резерва в случае отказов основных элементов для весьма ограниченного множества аномальных ситуаций. Предпочтительность выбираемой конфигурации рассматривается лишь с позиций ее работоспособности применительно к текущему состоянию системы без учета влияния этого выбора на ее дальнейшее функционирование. Новые подходы предполагают формирование конфигурации БВК ПО не только по состоянию ее элементов в текущий момент времени, но и с учетом изменения условий ее функционирования на последующих интервалах на основе сценарного подхода [1].

Сценарное прогнозирование деградации информационно-вычислительных ресурсов ...

Захаров Иван Вячеславович

Вместе с тем модели и методы общей теории надежности, теории живучести сложных систем, теории вычислительных систем, теории реконфигурируемых систем проработаны достаточно глубоко, однако основной вопрос – сложность их совместного применения – решен только для ограниченного числа частных случаев, поскольку композиция предлагаемых моделей и методов оказывается крайне трудоемкой. Кроме того, существенный недостаток классических методов теории вычислительных систем применительно к деградирующим структурам заключается в детерминированных подходах к усредненным оценкам характеристик их функционирования, в то время как для БВК рассматриваемого класса существенным аспектом является вероятностная оценка выполнения задач.

Оценка характеристик вычислительных систем в стационарной конфигурации

Пусть структура гетерогенного иерархически-сетевого БВК ПО задается как совокупность элементов БВК и связей между ними. Элементами структуры являются вычислительные узлы, а связи в структуре заданы в виде матрицы смежности. Задан типовой для данного БВК набор задач. Необходимо определить зависимость целевого эффекта применения БВК от времени с учетом его деградации под неблагоприятным воздействием внешних и внутренних факторов.

Задача моделирования включает подзадачи:

• -    оценка характеристик БВК в стационарной конфигурации;

• -    оценка целевого эффекта;

• -    моделирование структурно-параметрической деградации в процессе эксплуатации.

Для оценивания производительности гетерогенного иерархически-сетевого БВК ПО в стационарной конфигурации с учетом разнородности задач по ресурсоемкости и критичности он представляется как сеть массового обслуживания с узлами типа M/G/1. Принятые при этом допущения кратко обосновываются следующими соображениями. Вычислительные задачи поступают в БВК ПО от значительного количества абонентов и имеют несколько уровней приоритета, что позволяет считать их суммарный поток простейшим. Для подвижного объекта определенного целевого назначения можно выделить конечное число определенных режимов функционирования, следовательно, ограничить для БВК типовые наборы вычислительных задач и определить их параметры с учетом репликации в соответствующих режимах, связности по данным и управлению, а также возможности использования специализированных модулей для решения общих задач и централизованного решения специализированных задач [2]. Процесс решения задачи представляется в виде ее прохождения последовательности обслуживающих устройств от нулевого уровня структуры (уровня вычислительных модулей) до вершины, последовательно через интерфейсные модули промежуточных уровней [3]. Время решения задачи в БВК определяется суммой времени решения задачи назначенными узлами (модулями), которые складываются из случайного времени ожидания, зависящего от производительности и нагрузки узла, и времени непосредственного выполнения, зависящего от быстродействия модуля и ресурсоемкости задачи. Диспетчеризация обеспечивает равномерное в смысле коэффициента нагрузки распределение задач по вычислительным модулям.

Получив известными методами теории массового обслуживания вероятности решения задач за директивный срок p i , i = 1..., m [3], рассчитаем показатели, позволяющие свернуть быстродействие узлов, объем задач и их директивные сроки:

• •    вероятность успешного решения набора задач на заданном интервале t ^ц

m

P = П р^' ;

i = 1

• •    вычислительная мощность БВК ПО

m v=Л^;

• •    его вычислительная способность     ^{i = 1}

v 0 = max v ( Л ) ,

Л

m где Ai - интенсивность потока i-го типа задачи; A = ^2i, 0 < в i < 1 - коэффициент кри-

A тичности задачи, Y = ~ . i Л

i = 1

Пример зависимости вычислительной мощности БВК ПО от интенсивности потока вычислительных задач, выраженной в единицах быстродействия, представлен на Рисунке: показаны графики для режимов однократного, дублированного и мажоритарного просчета задач, обеспечивающих защиту от аппаратных сбоев.

Сценарное прогнозирование деградации информационно-вычислительных ресурсов ...

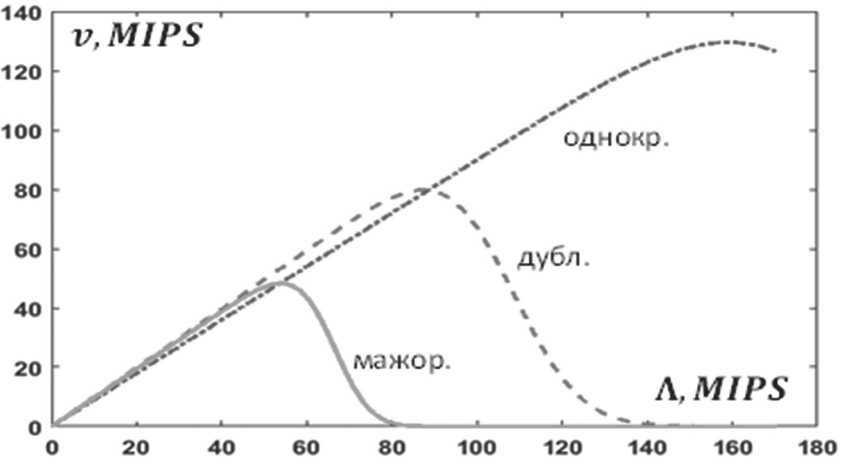
Рисунок. Пример оценки вычислительной мощности БВС Источник: график составлен авторами.

Указанный способ при достаточно низкой вычислительной сложности обеспечивает учет иерархически-сетевой структуры БВК ПО, а также вероятностный характер получаемой оценки, который позволяет перейти к вероятностным оценкам качества решения целевой задачи подвижного объекта.

Оценка целевого эффекта

Оценивание целевого эффекта, достигаемого применением БВК ПО, производится следующим образом [4]. Пусть целевые задачи Z^^.Z '- M ) циклограммы Z работы ПО могут быть реализованы в одном из функциональных режимов БВК с заданным коэффициентом 0 <  C j <  1 ценности функционального режима, а О , ) - набор вычислительных задач, решаемых БВК ПО при реализации целевой задачи Z ( i ) в j -м функциональном режиме.

Показатель результативности выполнения циклограммы Z выражается в виде где X cj )=1 vj, Zi = i -z^z задач;

' 0, zQ

L = C П Z . - X c П- i : Z⁽ ° eZ ₀ i : Z ⁽ ° e Z 0 ' выполнена

1, Z ( ' ) не выполнена

2 ₀ c Z - множество обесценивающих

c j ) - весовой коэффициент важности задачи Z ( i ) ; X c j ) = 1, V j .

i Z i e Z 0

Его ожидаемое среднее значение составляет

L = M [ L ]= C , п P^ - х c ' ) j i : Zi e Z      i - Z^ e Z₀

где Pj' ) - вероятность решения задачи Z (') .

Обозначая через Р^^вк вероятность решения в БВК ПО набора вычислительных задач

^('), K по — условный (без учета БВК) коэффициент оперативной готовности ПО на интервале решения задач циклограммы, а получим

P = П P^ K i : Z^{( , )}e2 0

■ е c j ) e i : Z^{( i )}«2 ₀

L = K _no ■ Cj ■ P = K _no ■ J .

Величину AJ назовем динамическим коэффициентом результативности функциони рования БВК ПО в режиме ^ :

A J ( ^ ) = C ■ P ( £ ) = C ■ v ^ = С ^ ■ v ( ^ ) ,

Л где Л^ - интенсивность потока вычислительных задач; v(^) = Л^ ■ P(^) - вычислительная мощность БВК; С^ - коэффициент ценности вычислений.

Интегральный коэффициент результативности функционирования ВС ПО определяется как t2

J ( t 1 ; t 2 ) = -7-J^A J ( ^т) d ^T • t ² t ¹ 1 1

Таким образом, выдвинутые показатели находятся в пропорциональной зависимости с показателями результативности выполнения циклограммы целевых задач ПО и произ- водительности БВК ПО. Видно, что при равноценных задачах cj) = c, V i',Vj и неразличимых функциональных режимах ^i = ^j, Vi,Vj показатель AJ имеет смысл коэффициента оперативной готовности БВК ПО.

Моделирование структурно-параметрической деградации

В силу неопределенности внешних воздействий принимается сценарный подход, при котором рассматривается множество сформированных, например, экспертными методами, наборов параметров («сценариев») условий функционирования. Сценарии имеют определенный вес и охватывают спектр возможных ситуаций. На основе сценариев строится прогнозирование траекторий деградации БВК ПО с учетом динамики внешней среды и выработанного элементами системы ресурса и формируются соответствующие оценки ее результативности функционирования для данного сценария, что позволяет оценить интегральный полезный эффект на интервале функционирования. Поэтому процесс деградации БВК ПО не может быть достаточно адекватно охарактеризован прогнозируемым временем функционирования, поскольку он имеет не только исправное и неработоспособное, но и промежуточные состояния, соответствующие постепенной деградации как системы в целом, так и ее элементов.

Прогнозирование деградации БВК ПО требует получить зависимости вероятностей пребывания ее элементов в работоспособном состоянии p ( t ) = p i ( 1 1 g i , H ) от времени t e [ 1 ₀; t_s ] для некоторой фиксированной конфигурации G и сценария условий функционирования H .

Применительно к иерархически-сетевому БВК ПО данный подход реализуется следующим образом. Деградацию целевого эффекта применения БВК ПО будем оценивать че-

Сценарное прогнозирование деградации информационно-вычислительных ресурсов ...

рез математическое ожидание коэффициента интегральной результативности функционирования БВК ПО в момент времени. Тогда, исходя из обоснования показателей производительности БВК ПО (1), (2), необходимо из p ( 1 1 H , G ) , полученного путем моделирования физических процессов [3], построить «траекторию» деградации математического ожидания производительности V ( t ) БВК ПО и далее - коэффициента Л J ( t ) результативности его функционирования.

В рамках поставленной задачи исчерпывающим описанием деградации структуры системы следует считать законы распределения вероятностей для всех ее возможных состояний в любой момент времени t >  1 0 . Предположим, что известно правило ^ : ®^ v расчета показателя производительности v БВК ПО исходя из состояния © его элементов, а также правило ^ : p ^ F [ V ] , ставящее в соответствие вероятностям p закон распределения случайной величины показателя v ^ˆ производительности БВК ПО и его параметры F . Отсюда, имея p ( t ) , траекторию деградации математического ожидания V ( t ) случайной величины V ( t ) можно выразить как V [ p ( t ) ] .

Поскольку решение данной задачи в общем виде затруднительно (прежде всего, не определено правило у/ ), для построения приближенной аналитической зависимости V ( t ) представляется целесообразным использовать особенности иерархически-сетевой структуры БВК ПО, а в качестве показателя производительности принять вычислительную способность (2). Для этого путем, например, имитационного моделирования необходимо получить P ( £ , v ) - вероятности решения задач в функциональном режиме (далее - ФР) £ при значении v показателя вычислительной способности. Зависимость P ( £ , v ) можно рассматривать как задаваемую параметрически через P ( £ , G ) - вероятность успешного решения задач и v ( G ) - вычислительную способность БВК в аппаратной конфигурации G . Тогда, поскольку v является дискретной величиной, принимающей конечное число значений, равное числу возможных аппаратных конфигураций, а v – непрерывной, то для каждого ФР £ известными методами, например, наименьших квадратов, аппроксимируется зависимость P ^ ( v ) , заданная множеством точек ( V k ; P k ) ^ . При этом учитывается, что P ( £ ,0 ) = 0, P ( £ , G ) < 1 V £ , V G . Таким образом, построение зависимости P ( £ , v ) можно схематично выразить в виде

{ v ( G k ) ; P ( £ k , G k ) } ^ { ( V k ; P k ) ^ P P ( £ , v ) , P ( £ ,0 ) = 0, P ( £ , v ) < 1 V £ , V v .

Заключение

Оценивание «вычислительной мощности» как определяющего показателя БВК дает возможность свернуть параметры задач и быстродействия вычислительного комплекса и отражать структурную деградацию нижних уровней иерархии (отказов вычислительных узлов) на параметрическую деградацию характеристик (производительности вычислительных модулей) верхних уровней системы. Это позволяет перейти к обоснованию показателей качества БВК на более высоком уровне абстракции по сравнению с классическими (быстродействием, пропускной способностью каналов, временем доступа к памяти, вероятностью безотказной работы узлов и др.). При этом обоснованные допущения позволяют формализовать возможные структуры БВК различных вариантов топологии широкого класса и стратегии управления ресурсами системой. В качестве целевой функции использована оценка интегрального коэффициента результативности функционирования БВК ПО в условиях детерминированных и случайных внутренних и внешних факторов с учетом его структурно-параметрической деградации.

Таким образом, предложенный подход, в отличие от известных, учитывает анализ условий функционирования БВК ПО, прогнозирование деградации с учетом воздействующих факторов и остаточного ресурса и позволяет оценить предельно возможную результативность его функционирования за срок активного существования ПО в целях решения оптимизационных задач управления. Его исследование показало непротиворечивость результатов моделирования и теоретических положений в области анализа многомодульных реконфигурируемых вычислительных систем. Следовательно, его применение представляется целесообразным при решении вопросов синтеза структуры и управления перспективных БВК ПО [5; 6].