Scheduling of Generating Unit Commitment by Quantum-Inspired Evolutionary Algorithm

Generating unit commitment is one of the important problems, which plays an important role in optimal and economic performance of power systems during their operation. In this paper, a UC problem with the objective of minimum operation cost and constraint is solved. Among the method which has been previously used to solve the generating UC problem, priority list [1], dynamic programming [2], Lagrangian relaxation [3], mixed-integer programming [4] and the branch-and-bound algorithm [5] can be mentioned.In Recent years, evolutionary algorithms (EAs) like genetic algorithm (GA) [7], simulated annealing (SA) [8], evolutionary programming (EP) [9], particle swarm optimization (PSO) [10] and hybrid methods [11], have been employed successfully to solve the UC problems. These methods are based on the stochastic optimization techniques, and they operate with various search mechanisms on a group of selected solutions.

Quantum-Inspired Evolutionary computation is a branch of Evolutionary computation, which special principles of mechanic quantum like interference, superposition and uncertainty are, employed [12]. Quantum-Inspired Evolutionary algorithm will be reach to a better balance between the detection and exploitation of the solution space, by means of concepts and Fundamentals of quantum computing such as quantum bits (Q-bits), quantum gates (Q-gates) and conformity of these states. In addition, compared with the conventional Evolutionary algorithms in a small population, it can be reach to better solutions. In [13], conformity performance of QEA for combinatorial optimization problems has been showed. In this paper, QEA has been used to solve the UC problem. For this purpose, firstly the unitscheduling problem is solved by QEA-based UC method (QEA-UC) and then economic dispatch problem is resolved. The presented algorithm has been compared with the proposed algorithm in [14]. In section 2 the formulation of the UC problem is presented, and in section 3 fundamentals and procedure of QEA is described. In section 4, we introduce the proposed QEA-UC method and in section 5 we will have the simulation results and finally in section 6 the conclusions are presented.

• II. Problem Formulation

The purpose of solving the UC problem in this paper is minimizing the production cost, which include the fuel cost and the start-up cost during a certain period of time (24 Hours). The formulation of this optimization problem is presented in equations (1) to (8):

Objective function:

HN min. FH=EE[ Fkh (Pkh)+STkh (1 - uk (h -i))] ukh k=1 k=1

Fuel cost function:

Fkh (Pkh ) = ck (Ph )2 + bk (Pkh ) + ak

Start-up cost function:

ST kh =^

HSC, ff MDT. < TOf < MDT + CSH. k      kk      kk

CSC, ffTff > MDT + CSHk kk    kk

The constraints of UC problem which considered in this paper are as follows:

• 1)    Load Request supply constraint

N

E Pkhukh = Dh(4)

k = 1

• 2)    Spinning reserve constraint

N

E Pk (max)ukh ^ Dh+Rh k=1

• 3)    Unit production constraint

≥ Pn ≥ unhPn(min)

• 4)    Minimum up time limit

Tnon ≥ MUTn

• 5)    Minimum down time limit

Tnoff ≥ MDTn

The notation list used in this paper is as follows:

N : Number of generating units;

• H : The total hours of scheduling period;

• n : Index of unit;

• h : Index of time;

P_nh : Control variable for the generation of unit n at hour h;

U nh : Control variable for the on/off status of unit n at hour h;

F H : Total system production cost within h hours;

F_nh(P_nh) : Fuel cost function of unit n at hour h ;

• a n ,b n ,c n : Cost function parameters of unit n;

ST_{nh :} Start-up cost of unit n at hour h ;

HSC n /CSC n : Hot/cold start-up cost of the n th unit ;

MDT_n/MUT_n : Minimum down/up time of the n th unit;

CSH_n: Cold start hours of unit n_;

T n^off : Duration during which n unit is continuously OFF;

T_n ^on : Duration during which unit is continuously ON;

D h : System peak demand at hour h;

R_h : Spinning reserve at hour h;

P_n ( _max ) : Maximum/minimum output limit of unit;

• III. Quantum-Inspired Evolutionary Algorithm

• 3.1    Presentation

The same as other evolutionary algorithms, the QEA method consist of computing functions and also specific population dynamics. In quantum computations, a Q-bit is smallest information unit that stored in two states, instead of binary numbers in the previous evolutionary methods. A string of Q-bits form an individual Q-bit that can include all the possible states in the search space. QEA only needs a small initial population to produce a variant and proper population to explore the solution. A Q-gate is a QEA variable parameter that becomes 0 or 1 for every Q-bit and gradually tends to the best solution by variation decrease, during the optimization process. So by definition of Q-bit, a unique Q-bit is represented and forms a search state. Moreover, for every individual Q-bit, Q-gate only shows one operation state (on or off). So the QEA mechanism creates a balance between exploration and extraction of solution space. In next section, the concept of Q-bit and steps of QEA method is described.

A Q-bit is the smallest unit of information. It can be represented as:

Where α and β are two numbers that satisfy the equation (|α|2 +|β|2 =1) (The two numbers that is located on the first quarter of coordinate axis and sum of their square is equal to 1), where |α|2 and |β|2 are the probability of happenning “0” and “1” respectively.

। ^>= a o>+ в 1

A unique Q-bit that consists of m Q-bit is showed as follows:

1 [ 1	2	3  …	атЛ ]	(11)
	2	3  …

The Q-bits exist in every unique Q-bits, show the possible states of nth unit during hth hour. So for m Q-bit, we have 2m states for all the h periods. The unique Q-bit for all the α and β is equal to the same value of 0.5 which all the possible states represent by the same probability as follows:

| >=∑

2m

k=V

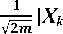
Where Xk is the kth state of the binary string solution (X1, X2,…, Xm) and every Xi is either 0 or 1.

For example for a unique Q-bit with two Q-bit:

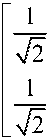
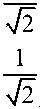
Where the Q-bit states are unique as follows:

|00>+ |01>+ |10>+ |11>      (14)

In which the probability of all states are ¼. So for a unique Q-bit with 2 Q-bits (particle), we have 4 states for all the h periods.

• 3.2    Qea Methods

QEA method uses Q-bit for population variation. According to QEA process, the binary solutions of X, obtain from the unique Q-bit and at the end of any iteration, the particles (Q-bit) will update for next step. The details of the QEA mechanism for solving the objective function f(x), and control the binary variation X are as follows:

Step 1 : t is the generator counter, set t=0.

Step 2: Initialize (t) Q: (t) Q is a group of unique Q-bits that is initialized at t=0. So we will have: Q (t) = [Q1t, Q1t, … , Qnt ]

Where subscript n is the total number of unique Q-bit and q j ^t is the j th particle (Q-bit) for t th generator.

q^t j

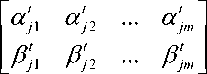
Where j=1,2,…,n is the number of every particle and m is the particle string length. If all the α_i j and β_i j ^t is initialized with the same value of 0.5 , the probability of happening “0” or “1” state is equal for every Q-bit.

Step 3: X(t) is selected by observing Q(t):

X(t) =[ X₁^t , X₂^t ,…, X_n^t ] is a group of binary solutions which are determined by Q(t) observation. X j is the binary solution that is obtained by q j ^t observation: X j ₁^t =[x j ₁^t,…, x j ₂^t , x j _n^t] where X_i j ^t is binary solution for particle number j, in the first iteration and for generator number t . It is determined by comparing |β ij ^t|² to a random number between 0 and 1, in which if the number was smaller than |β ij ^t|², X ij will be equal to “1” and if not, will be equal to “0”:

1, random [0,1] < |в|2

0,        otherwise

Step 4: Evaluate X(t):

The cost function values which are the same as objective function is calculated by considering all the

X(t)s, and the best X(t) with the least cost will be obtained.

Step 5: Storing the best solution of X(t) into B(t):

B(t) is a matrix including the best solutions among all of the particles.

Step 6: t = t+1.

Step 7: Determining X(t) by observing Q(t-1).

Step 8: Evaluating X(t).

Step 9: Updating Q(t) by Q-gate:

A Q-gate is a variable parameter in QEA that update Q-bits, and in updated Q-bit (αijt and βijt) the equation |α ijt| 2 + |βijt |2 = 1 must be satisfied. In QEA, the rotation gates are considered. The rotation gate is a conversion matrix that performs update operation:

U ( A j =

cos( A 6 / ) sin(A ^ t j

- sin( A ^ .) cos(A()\)

а

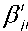
= U ( А 0^ )

a t

WhereΔθ is the rotation angle that its magnitude can be obtained according to table 1 (reference [14]).

Table 1: The Rotation Angle

4	bt	Quadrant	(  )≤  (  )	Δ
0	1	Ι/ΙΙΙ	false	+θ
0	1	ΙΙ/IV	false	-θ
1	0	Ι/ΙΙΙ	false	-θ
1	0	ΙΙ/IV	false	+θ
0	1	×	true	0
1	0	×	true	0
0	0	×	×	0
1	1	×	×	0

X is the final solution of every period, b is the best solution of every period, f(x) and f(b) are the objective function for X and b values. As it can be seen from table 1, when the values of f(x) and f (b) are equal, the rotation angle is zero and the conversion matrix will become a unit Matrix, which will be unchanged when it is multiplied by Q-bit. For the case that X and b are different and also f(x) is bigger than f (b), the rotation angle according to reference [14] will be equal to θ = 0.02π but If f (x) is less than f (b), this means the response obtained in this iteration was better than the previous Solution of and this Result as the best answer can be used in the next iteration.