SD-AREE-I Cipher: Amalgamation of Bit Manipulation, Modified VERNAM CIPHER & Modified Caesar Cipher (SD-AREE)
Автор: Somdip Dey
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 6 vol.4, 2012 года.
Бесплатный доступ
This paper presents a new combined symmetric key cryptographic technique, which is generally an amalgamation of Bit Manipulation, generalized Modified Vernam Cipher, Single Bit Manipulation and Modified Caesar Cipher. The technique proposed here is basically an advanced and upgraded module of SD-AREE cryptographic method, which is based on Modified Caesar Cipher along with Bit Manipulation and the SD-AREE module is very useful in excluding any repetition pattern from a message that is to be encrypted. The proposed method, SD-AREE-I Cipher, is a complete cipher method and unlike its predecessor, SD-AREE, does not need to be added to other cryptographic methods to make those methods stronger. SD-AREE-I method is used to encrypt/decrypt different file formats and the results were very satisfactory. This method is unique and strong because the method contains feedback mechanism and generates new encrypted output every time even with slightest change in the input file (message). The proposed method can also be used for network security.
Cryptography, Repetition exclusion, Bit Manipulation, Decryption, SD-REE, SD-AREE, Modified Caesar Cipher
Короткий адрес: https://sciup.org/15011430
IDR: 15011430
Текст научной статьи SD-AREE-I Cipher: Amalgamation of Bit Manipulation, Modified VERNAM CIPHER & Modified Caesar Cipher (SD-AREE)
Published Online June 2012 in MECS and Computer Science
In modern world, security is a big issue and securing important data is very essential, so that the data can not be intercepted or misused for illegal purposes. For that reason, different cryptographic methods [7][8][9] are used by different organizations and government institutions to protect their data online. But, cryptography hackers are always trying to break the cryptographic methods or retrieve keys by different means. To deal with this problem, cryptographers come up with different new ideas of protecting the data using different cryptographic means. SD-AREE-I is one such cryptographic method. Dey et al. already proposed a cipher technique, called SD-AREE [4][5], to exclude the repetitive characters in a message to be encrypted and the technique is a type of symmetric key cryptography [7][8][9].
The modern day cryptographic methods are of two types: (i) symmetric key cryptography [7][8][9], where the same key is used for encryption and for decryption purpose. (ii) Public key cryptography [7][8][9], where we use one key for encryption and one key for decryption purpose.
Symmetric key algorithms are well accepted in the modern communication network. The main advantage of symmetric key cryptography is that the key management is very simple. Only one key is used for both encryption as well as for decryption purpose. There are many methods of implementing symmetric key. In case of symmetric key method, the key should never be revealed / disclosed to the outside world or to other user and should be kept secure.
SD-AREE method, proposed by Dey et al. [] [], is basically a new implementation of modified Caesar Cipher in securing information in a better way. SD-AREE-I is also a symmetric key cryptographic method and the best part of this method is every time the cipher technique generates new encrypted output results if there is a slightest change in the input message. This technique was only achievable after implementation of generalized modified Vernam Cipher with feedback mechanism and advanced bit manipulation technique.
In this paper the author present the cryptographic technique SD-AREE-I, which is a both bit level and byte level cryptographic method. First the message is broken up into bits and it is saved in a matrix, then Matrix– cycling Operation is performed on that matrix for random number of times. After that the generalized modified Vernam Cipher with feedback mechanism is executed on the data. Then we apply Single Bit Manipulation followed by a modified form of Advanced Caesar Cipher Cryptographic Method [4] [5] [6]. In cryptography, a Caesar cipher, also known as a Caesar's cipher or the shift cipher or Caesar's code or Caesar shift, is one of the simplest and basic known encryption techniques. It is a type of replace cipher in which each letter in the plaintext is replaced by a letter with a fixed position separated by a numerical value used as a "key". Caesar Cipher is or was probably the very first encryption methodology. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a shift of 3, A would be replaced by D, B would become E, and so on.
-
II. Encryption Method
SD-AREE-I Cipher follows the following algorithm:
Step-1) generate Code and poer_ex from the password for future use in encryption
Step-2) Bit Level Matrix Cyclic Operation
Step-3) Modified Vernam Cipher with Feedback mechanism
Step-4) Single Bit Manipulation
Step-5) Modified Caesar Cipher (SD-REE)
The aforementioned steps can be further clarified with the block diagram of the proposed method:
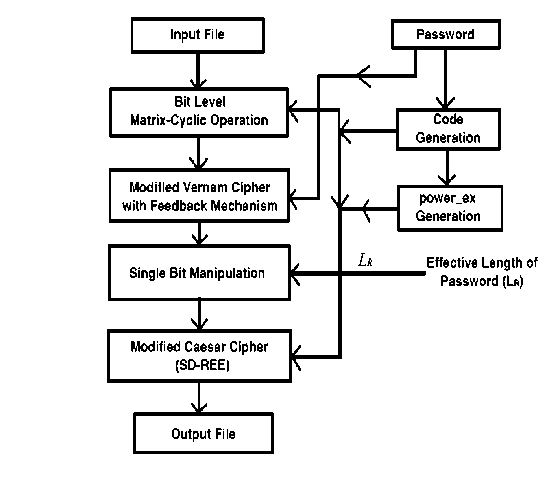
Figure: Block Diagram of SD-AREE-I Cipher
Now, we elaborately explain each step followed in the proposed method.
-
A. Generation of Code and power_ex from the Symmetric Key:
The key is provided by the user in a string format and let the string be ‘pwd[]’. From the key, which is provided by the user, we generate two numbers: ‘code’ and ‘power_ex’, which will be used for encrypting the message. First we generate the ‘code’ from the pass key.
Generation of code is as follows:
code = (pseudo_code Modulus 16).
If code==0, then we set code =pseudo_code
The Algorithm for this is as follows:
Let us assume, pwd[] = key inserted by user pp= 2i , i=0,1,2,……..n; n ∈ N.
Note: i can be treated as the position of each character of the key.
Step 1: p[] = pwd[]
Step 2: pp = 2i
Step 3: for (i=0;i < strlen(pwd); i++)
p[i] = pwd[i];
p[i] = p[i] * strlen(pwd) * pp; csum = csum + p[i];
Step 4: while (csum ≠ 0)
c = csum Modulus 10; pseudo_code=pseudo_code +c; csum = csum / 10;
Step 5: code = (pseudo_code Modulus 16);
Note: strlen(pwd) is string-length of the pwd[] (key).
Generation of power_ex is as follows:
Now, we generate power_ex from the pseudo_code generated from the above step. We add all the digits of the pseudo_code and assign it as temporary_power_ex. Then we do modular operation on temporary_power_ex with 3 and save the resultant as power_ex.
i.e.
power_ex = (temporary_power_ex Modulus code)
If power_ex == 0 OR power_ex == 1, then we set power_ex = code.
For example, if we choose the password, i.e. the key to be ‘hello world’. Then,
Length of pwd = 11
code = 10
power_ex = 4
Thus, we generate code and power_ex from the key provided by the user.
-
B. Bit Level Matrix-Cyclic Operation:
Now, after the generation of ‘code’ and ‘power_ex’, the text, which needs to be encrypted, is taken up as a string and each character (for ASCII encoded text) or byte is broken up into bits (8-bit pattern). Then a matrix table is formed, which is of dimension (8 x 8), provided that the number of bytes is equal or more than 8, and keep on forming such matrices until all bytes of the message to be encrypted have been transformed into bit-wise matrix format. If the number of bytes is less than 8 then the matrix formed will have the dimension (m x 8), where ‘m <=8’. In this matrix, we save the bits of each byte in the column of the matrix and save each byte in the row of the matrix. For example: if the text to be encrypted is ‘ABd’, then it can be represented in matrix form after extraction of bits in the following fashion:
|
Matri x (3 x 8) |
Bit 7 (MS B) |
Bi t 6 |
Bi t 5 |
Bi t 4 |
Bi t 3 |
Bi t 2 |
Bi t 1 |
Bit 0 (LSB) |
|
A -> |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
B -> |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
d -> |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
Note: In the above example matrix we can see that the number of bytes is less than 8, so only 1 matrix is formed and the dimension of the matrix is (3 x 8), where m=3, which is <8.
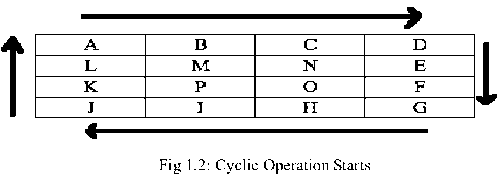
Now, after the matrices are created we perform cyclic operation [2] on the matrix several times, i.e. multiple times and form a new set of values.
Matrix-cyclic [2] operation can be explained in the following example:
|
A |
B |
C |
D |
|
L |
M |
N |
E |
|
K |
P |
O |
F |
|
J |
I |
H |
G |
Fig 1.1: Real Matrix
|
L |
A |
B |
C |
|
K |
N |
O |
D |
|
J |
M |
P |
E |
|
I |
H |
G |
F |
Fig 1.3: Matrix After Cyclic Operation
We perform the cyclic operation ‘n’ number of times, where n= code, which is generated from the key. After the cyclic operation we again change back the binary value of the bytes into its decimal form i.e. the ASCII form.
Algorithm for this whole step:
Step 1: extract all bytes of the message into a string
Step 2: extract the bits of each byte from the string i.e.
convert ASCII value of each byte to binary form
Step 3: save the bits in a 2 dimension array such as a[r][c], where r -> row and c -> column
Step 4: r = each byte c = each bit of that byte
Step 5: perform cyclic() ‘n’ times on a[r][c], where n = code
Step 6: convert the binary form to ASCII value (decimal form)
Step 7: store the result in text[]
Note: text[] is an array, where the ASCII value of the bytes after bit level encryption is stored.
-
C. Modified Vernam Cipher with Feedback:
The module of modified Vernam Cipher, which is used in this method is a concept proposed by Nath et al. [1][2]. Nath et al. in their cryptographic method, called TTJSA [1], has proposed an advanced form of generalized modified Vernam Cipher with feedback mechanism. For this reason, even if the data is slightly changed, the encrypted output generated is very different from the other outputs.
TTJSA method is a combination of 3 distinct cryptographic methods, namely, (i) Generalized Modified Vernam Cipher Method, (ii) MSA method and (iii) NJJSA method. To begin the method a user has to enter a text-key, which may be at most 16 characters in length. From the text-key, the randomization number and the encryption number is calculated using a method proposed by Nath et al. A minor change in the text-key will change the randomization number and the encryption number quite a lot. The method have also been tested on various types of known text files and have been found that, even if there is repetition in the input file, the encrypted file contains no repetition of patterns.
In SD-AREE-I Cipher method we have only used the modified Vernam Cipher module of TTJSA by Nath et al. Here, Code represents the randomization number and power_ex represents the encryption number. All the data in the file are converted to their equivalent 16 bit binary format and broken down into blocks.
Algorithm for Modified Vernam Cipher with feedback mechanism is as follows:
-
1) Algorithm of vernamenc(f1,f2):
Step 1: Start vernamenc() function
Step 2: The matrix mat[16][16] is initialized with numbers 0-255 in row major wise order
Step 3: call function randomization() to randomize the contents of mat[16][16].
Step 4: Copy the elements of random matrix mat[16][16] into key[256] (row major wise)
Step 5: pass=1, times3=1, ch1=0
Step 6: Read a block from the input file f1 where number of characters in the block 256 characters
Step 7: If block size < 256 then goto Step 15
Step 8: copy all the characters of the block into an array str[256]
Step 9: call function encryption where str[] is passed as parameter along with the size of the current block
Step 10: if pass=1 then times=(times+times3*11)%64 pass=pass+1
else if pass=2 then times=(times+times3*3)%64
pass=pass+1
else if pass=3 then times=(times+times3*7)%64
pass=pass+1
else if pass=4 then times=(times+times3*13)%64
pass=pass+1
else if pass=5 then times=(times+times3*times3)%64 pass=pass+1
else if pass=6 then times=(times+times3*times3*times3)%64 pass=1
Step 11: call function randomization() with current value of times
Step 12: copy the elements of mat [16][16] into key [256]
Step 13: read the next block
Step 14: goto Step 7
Step 15: copy the last block (residual character if any) into str[]
Step 16: call function encryption() using str[] and the no. of residual characters
Step 17: Return
-
2) Algorithm of function encryption(str[],n):
Step 1: Start encryption() function
Step2: ch1=0
Step 3: calculate ch=(str[0]+key[0]+ch1)%256
Step 4: write ch into output file
Step 5: ch1=ch
Step 6: i=1
Step 7: if in then goto Step 13
Step 8: ch=(str[i]+key[i]+ch1)%256
Step 9: write ch into the output file
Step 10: ch1=ch
Step 11: i=i+1
Step 12: goto Step 7
Step 13: Return
-
3) Algortihm for function randomization():
The randomization of key matrix is done using the following function calls:
Step-1: call Function cycling()
Step-2: call Function upshift()
Step-3: call Function downshift()
Step-4: call Function leftshift()
Step-5: call Function rightshift()
Note: Cycling, upshift, downshift, leftshift, rightshift are matrix operations performed (applied) on the matrix, formed from the key. The aforementioned methods are the steps followed in MSA algorithm [2] proposed by Nath et al.
After the execution of modified Vernam Cipher, each block is written down into the file and further processed by next steps of the cipher method
-
D. Single Bit Manipulation:
The Single Bit Manipulation technique was proposed by Dey et al. in their SJA-I [3] algorithm. In this stage, we convert each byte / character of the message to be encrypted, to its binary equivalent. Now, length of password is considered for bit left shift. i.e., Number of bits to be shifted to left will be decided by the length of password. Let L be the length of the password and L R be the number of bits to be rotated to left and reversed (i.e. L R is the effective length of password). The relation between L and L R is represented by equation (1).
L R =L mod 7 ------ eq. (1)
where ‘7’ is the number of iterations required to reverse entire input byte.
After this, the last two extreme positions of the bits are swapped with each other to generate the final output character, i.e. if the bit format is like [B 8 B 7 B 6 B 5 B 4 B 3 B 2 B 1 ] for input byte then B 8 will be swapped with B 1 and B 7 will be swapped with B 2 . Thus, the binary equivalent of the output byte will become: [B 1 B 2 B 6 B 5 B 4 B 3 B 7 B 8 ] after swapping of bits.
For example, let Chin be any random character / byte from the message. Then its binary equivalent will be: [B8B7B6B5B4B3B2B1]. If the password provided for encryption is “somdi”, then LR=5 and the bits will be shifted by 5 positions to their left. Thus CHin will become [B3B2B1B8B7B6B5B4] after left shift and then [B3B2B1B4B5B6B7B8] after reversing. Then, according to the algorithm the bits of extreme two sides are swapped with each other at a time. Thus, the resultant binary format is [B8B7B1B4B5B6B2B3].
Cin [B 8 B7B 6 B5B4B 3 B2B1]
[B 8 B7B1B4B5B 6 B2B 3 ] C out
-
E. Encrypting the Bit-Message using code and power_ex (Modified Caesar Cipher Method – SD-REE):
Now we use the code and power_ex, generated from the key, to encrypt the bit level encrypted text. We extract the ASCII value of each character of the text, which is produced after bit level encryption, and add the code with the ASCII value of each character. Then with the resultant value of each character we add the (power_ex)i, where i is the position of each character in the string, starting from ‘0’ as the starting position and goes up to n, where j=position of end character of the message to be encrypted, and if position = 0, then (power_ex)i = 0. It can be given by the formula:
text[i] = text[i] + code + (power_ex)i
If, ASCII value of text[i] > 255, then set text[i] = (text[i] Modulus 255)
Note: ‘i’ is the position of each character in the text and text[] is the message to be encrypted, where text[i] denotes each character of the text[] at position ‘i’.
Since, the value of (power_ex)i increases with the increasing number of character (byte) i.e. with the increasing number of string length, so we have applied the method of Modular Reduction [10][11] to reduce the large integral value to a smaller integral value.
To apply Modular Reduction we apply the following algorithm:
Step 1: n = power_ex * code * 10 //generate a random number ‘n’ from code and power_ex
Step 2: calculate nth prime number
Step 3: For (i=0; i Step 4: (power_ex)i Modulus (nth prime number) Step 5: replace the value of (power_ex) i with the value generated in Step 4 Step 6: Next i Following the previously mentioned steps, we can reduce the value of (power_ex)i to a significantly smaller usable number. Decryption: The main formulae used for decryption is: text[i] = text[i] - code - (power_ex)i Note: If, ASCII value of text[i] < 0, then set text[i] = (text[i] Modulus 255) ‘i’ is the position of each character in the text and text[] is the message to be encrypted, where text[i] denotes each character of the text[] at position ‘i’. IV. Results and Discussions In this section, we provide some test results of SD-AREE-I Cipher method and few of the test cases are provided in the following table: Input Message Encrypted Message St. Xavier’s is an autonomous college — OsA§!:$H^^15A0§ • IEu--™ Ó-7¸ÚRÕµ+^Ác 128 bytes of ASCII Value (1) hO^GRBOP— T\<~YU9t...£™mUzZ 0-zfá:,þ¡Z^ªÅb =2;“2E—j+^^UXf V -xglA 6"ai 6^a-ë=÷u 128 bytes of ASCII Value (5) BOP— T\<-YU9t-..£™mUzZ 0-zfá:,þ¡Z^ªÅbP%O£Ë^.å¶0rçÑ% <£, □6%(6A6tt* v^/c^u U a! 2;“2£ \+^UX , GIYDG-×g1A^6"áí^ïÓ •â At that time, barely a quarter of the world's independent states were democracies. But today, the number is 60 percent. Moreover, nearly two in every five states can reasonably be called liberal democracies. x8I9— 6и¥,бЖ^6# Ca € on!) A $0¥M^alk&%6heMc 7d$jeAO 9 6\„$h 0.#^ • □lAIS -~BT eofi y'£^; %£)HQa£Eb„6 [Hm^ $QU □-□“□ DUC^an"aU¥D IB (F^OAU>=huM;B*uU~Y$sa V. Effectiveness of Feedback Mechanism Used in Modified Vernam Cipher In this section, we prove that because of the incorporation of Feedback mechanism in Modified Vernam Cipher, the encrypted output generated by the cipher method is always different for even a slight change in the original message. We chose two test cases and did spectral analysis of the encrypted output of the test cases and the differences were clearly seen. The spectral analysis were different for different input data. Test Case No. Test Case (i) AAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAA AAAAAAAAA (1024 bytes of ‘A’) (ii) AAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAA B (1023 bytes of ‘A’ and 1 byte of ‘B’) Fig 2.1 shows the spectral analysis of the encrypted output of test case (i) and Fig 2.2 shows the spectral analysis of the encrypted output of test case (ii). Fig 2.1: Spectral Analysis of the Encrypted Output of Test Case (i) Acknowledgement SD is grateful to other fellow students of the Department of Computer Science of St. Xavier’s College [Autonomous], Kolkata, India. He also thanks Prof. Dr. Asoke Nath, the founder of Department of Computer Science, for his motivation and contribution in preparation of the paper.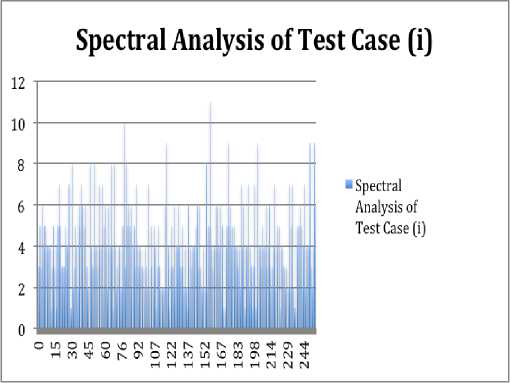
Список литературы SD-AREE-I Cipher: Amalgamation of Bit Manipulation, Modified VERNAM CIPHER & Modified Caesar Cipher (SD-AREE)
- Symmetric key cryptosystem using combined cryptographic algorithms - Generalized modified Vernam Cipher method, MSA method and NJJSAA method: TTJSA algorithm " Proceedings of Information and Communication Technologies (WICT), 2011 " held at Mumbai, 11th – 14th Dec, 2011, pp.1175-1180.
- Symmetric Key Cryptography using Random Key generator: Asoke Nath, Saima Ghosh, Meheboob Alam Mallik: "Proceedings of International conference on Security and Management (SAM'10" held at Las Vegas, USA Jull 12-15, 2010), P-Vol-2, pp.239-244.
- Somdip Dey, Joyshree Nath and Asoke Nath. Article: An Advanced Combined Symmetric Key Cryptographic Method using Bit Manipulation, Bit Reversal, Modified Caesar Cipher (SD-REE), DJSA method, TTJSA method: SJA-I Algorithm. International Journal of Computer Applications 46(20):46-53, May 2012. Published by Foundation of Computer Science, New York, USA.
- Somdip Dey, "SD-REE: A Cryptographic Method To Exclude Repetition From a Message", Proceedings of The International Conference on Informatics & Applications (ICIA 2012), Malaysia, p. 182 – 189.
- Somdip Dey, "SD-AREE: A New Modified Caesar Cipher Cryptographic Method Along with Bit-Manipulation to Exclude Repetition from a Message to be Encrypted", Journal: Computing Research Repository - CoRR, vol. abs/1205. 4279, 2012.
- Somdip Dey,Joyshree Nath,Asoke Nath,"An Integrated Symmetric Key Cryptographic Method – Amalgamation of TTJSA Algorithm, Advanced Caesar Cipher Algorithm, Bit Rotation and Reversal Method: SJA Algorithm", IJMECS, vol.4, no.5, pp.1-9, 2012.
- Cryptography and Network Security, William Stallings, Prentice Hall of India.
- Cryptography & Network Security, Behrouz A. Forouzan, Tata McGraw Hill Book Company.
- Cryptography and Information Security, V. K. Pachghare, Prentice Hall of India
- Peter Montgomery, "Modular Multiplication Without Trial Division," Math. Computation, Vol. 44, pp. 519–521, 1985.
- W. Hasenplaugh, G. Gaubatz, and V. Gopal, "Fast Integer Reduction," 18th IEEE Symposium on Computer Arithmetic (ARITH '07), pp. 225– 229, 2007.


