Себестоимость добычи в модели газового месторождения: исследование и применение

В отделе Методов проектирования развивающихся систем ФИЦ ИУ РАН на протяжении многих лет ведутся работы по динамическому планированию разработки нефтяных, газовых и газоконденсатных месторождений как для одного месторождения, так и для группы в целом [1-3]. С учетом современных основ эксплуатации газовых месторождений [4] на. основе имитационной модели группы газовых месторождений была разработана и внедрена. Система, планирования добычи газа, которая широко использовалась при расчетах для месторождений Западной и Восточной Сибири. Система, позволяет на. заранее заданном временном периоде рассчитывать объемы добычи газа, и технико-экономические показатели добычи в динамике по месторождениям. Был разработан ряд оригинальных математических моделей газовых месторождений и решено большое количество задач оптимального

«Московский физико-технический институт (государственный университет)», 2018

управления [5-6]. Одной из них является проблема оптимального экономического роста [7], решение которой основано на предложениях К. Эрроу [8].

Рассмотренные в [7] экономические показатели добычи газа в основном касались прибыли, дохода и других показателей, связанных с рыночной ценой, для чего имеются вполне обоснованные причины. Однако рыночная цена является слабо прогнозируемой экономической величиной даже на небольшом промежутке времени, что явно было продемонстрировано за последние несколько лет. В формулах, описывающих себестоимость, отсутствует рыночная цена,что дает себестоимости значительные преимущества перед другими вышеупомянутыми показателями. Поэтому можно отнести себестоимость к важнейшим экономическим показателям и уделить ей более серьезное внимание.

В последние годы был проведен ряд исследований по оптимизации себестоимости в смежных областях. Например, оптимальное планирование и развитие инфраструктуры для добычи сланцевого газа обсуждалось в [9], а в [10] рассматривалась общая оптимизационная модель для планирования производства и потребления энергоресурсов в различных отраслях промышленности. Повышенный интерес к проблематике себестоимости подтверждает актуальность темы, рассматриваемой в настоящем работе.

2.    Исследование себестоимости газового месторождения

Рассмотрим динамическую модель функционирования газового месторождения с взаи-мовлияющими скважинами [2]. Введём следующие обозначения:

Т— горизонт планирования;

N — действующий фонд добывающих скважин;

N — общий пробуренный и готовый к эксплуатации фонд добывающих скважин, являющийся естественным ограничением на действующий фонд добывающих скважин;

• q — средний дебит добывающих скважин;

• V — извлекаемый запас природного газа;

• с — стоимость природного газа.

Естественно, что все введенные обозначения являются положительными величинами. Между описанными выше переменными устанавливается взаимосвязь, которую запишем в виде системы дифференциальных уравнений q0

• ^V = ^-Nq, ^q = ^-a^Nq, a = ^0                   Ш

при начальных условиях V ⁰ > 0, q⁰ > 0. На фонд добывающих скважин накладывается следующее ограничение:

0 <  N <  N .                                 (2)

Предполагается, что N > 0. Капитальные затраты описываются в виде линейной функции г + kN, где г и к - постоянные коэффициенты. В настоящей работе рассматриваются две основные характеристики разработки месторождений: себестоимость добытого газа и прибыль, полученная от его реализации. Себестоимость газа определяется здесь как отношение капитальных затрат в период обустройства месторождения к добытому за плановый период объему природного газа:

^- s = г^.                       (3)

J qNdt

Прибыль есть разница между стоимостью всей реализованной продукции и всеми имеющимися издержками:

т ^р = ^cJ^qNdt -^{г -kN}.

В издержки включены только капитальные затраты, произведенные в предплановый период. Совокупные текущие затраты малы по сравнению с капитальными затратами, поэтому в дальнейшем их учитывать не будем.

Следует обратить внимание на то, что если вместо цены в (4) подставить себестоимость, то прибыль обратится в нуль. Таким образом, введенное понятие себестоимости оправдывает свое название «себестоимость». Однако если в определении прибыли будем учитывать коэффициент дисконтирования, то получаемая прибыль не будет равна нулю.

Проведём следующую замену переменных:

N ‘ = aN, N ‘ = aN,  V ‘ = aV = q, г’ = а^У, с’ = у.             (5)

k        k

При написании указанных переменных штрихи при них в дальнейшем опускаем. Двойное неравенство (2) будем понимать в новых переменных. Перепишем формулы (1), (3) и (4) в более удобной для дальнейшего анализа форме:

q = -Nq;

S = k

— у + N

т f qNdt о p=k

a

-

—

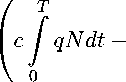
N

Ставятся две задачи оптимального управления: минимизация себестоимости добычи природного газа и максимизации прибыли от его реализации.

Задача 1. Требуется минимизировать функционал (7) при дифференциальной связи (6), начальном условии q° >  Du ограничении на управление (2).

Задача 2. Требуется максимизировать функционал (8) при дифференциальной связи (6), начальном условии q° >  Du ограничении на управление (2).

Легко показать, что минимум функционала (7) и максимум функционала (8) достигаются при N (t) = N на всем периоде планирования (t G [D, Т ]). Преобразовав формулы (7) и (8), получим две функции, зависящие от N и Т:

- —

S (N,T ) = k

— у + N q0(1 - e-Nт)

;

p(N, Т ) = К (cq⁰(1 - e^-Nт) - г -N } .

Далее найдем минимум функции (9) при фиксированном Т. Для этого найдем частную производную функцию (9) по N и результат приравняем к нулю. После преобразований получаем следующее уравнение:

e^Nт - 1 - NT - гТ = D.

(Ю)

Обозначим левую часть уравнения (10) через Ф(Т, N), где Т и N - положительные переменные. При этом параметр г считаем известной положительной фиксированной ве-личинои. Функция Ф(Т, N) определена и непрерывна при Т > D и при N > D, также данная функция имеет непрерывные частные производные дФ/дТ и дФ/dN при положительных значениях Т и N. причем дФ/дN = Т(eNT -1) > D. Легко показать, что для люоого То > D существует единственное No > D, при котором Ф(Tо,Nо) = D. Следовательно, по теореме о неявной функции при Т > D существует единственная положительно определенная 1           АТ АТ* /т\ функция N = N*(Т), удовлетворяющая уравнению (10).

Подставим функцию N*(Т) в уравнение (10). В результате приходим к тождеству eN (т)т — 1 — N*(Т)Т — zT = 0.                       щ)

Воспользовавшись последним тождеством, упростим формулу (9):

S (N *(Т),Т ) = ^^e^N *^(т)т.                             (12)

Интересно исследовать поведение функций N *(Т)Т, N *(Т) и S (N *(Т),Т) в зависимости от параметра Т Е (0, то). Исследование поведения этих функций будет полезно при решении ниже поставленной задачи.

Докажем последовательно три утверждения.

Утверждение 1. Функция N *(Т )Т определена, непрерывна и строго возрастает от 0 до то щш. Т >  0.

Разложим экспоненту в тождестве (11) в ряд Маклорена, и после преобразований получаем следующее двойное неравенство:

0 <  N * (т)т < V2T                         (із)

Устремляя в двойном неравенстве (13) параметр Т к нулю, получаем 1іт_т,_G(N*(Т)Т) = 0. Продифференцируем обе части тождества. (11) по Т. и после преобразований получим 7

(^N"(^Т)^Т)' = _e N * ( Т ) Т - 1 > °-                               ¹¹⁴¹

Это означает, что функция N*(Т)Т строго возрастает. Из тождества (11) вытекает следующий результат: lim_T ,^(N*(Т)Т ) = то. Утверждение 1 доказано.

Утверждение 2. Функция N *(Т) определена, непрерывна и строго убывает от то до 0 и} ш Т >  0.

Разделив обе части тождества (11) на Т, продифференцируем его по параметру Т. После преобразований получаем

(N *(Т))‘ =

eN *^(т)т - 1 — N *(Т )Te^N *^(т)т Т 2(eN *(т )т - 1)

Знаменатель дроби функции (15) положителен при Т >  0. Покажем, что числитель этой дроби отрицателен при тех же значениях Т. Числитель дроби равен нулю при Т = 0. Продифференцируем числитель дроби по параметру Т. В результате с учетом утверждения 1 при Т >  0 получаем

*

-N*(Т)Te^{N (т)т}(N*(Т)Т )‘ < 0.

Следовательно, числитель не обращается в нуль на интервале Т Е (0, то) при Т >  0 и он отрицателен. Значит, функция N*(Т ) строго убывает. Разделим все части двойного неравенства (13) на Т:

0 <  N *(Т) < У||.

Перейдя к пределу при Т ^ то, приходим к следутощему результату: 1іт_т N *(Т) = 0.

Разложим функцию e^{N (т)т} по формуле Маклорена 2-го порядка с остаточным членом в форме Пеано, и разложение подставим в тождество (11). В результате получаем

(N *(Т)Т)2

+ o(N*(Т)Т )² - zT = 0.

(TV *(т)т )²

п. учитывая 1ітт ,о(N*(Т)Т) = 0. пс-

1-

2z lim                 = 0.

т MG (N *(T))²T

В результате получаем limy ,_о N*(Т ) = то. Утверждение 2 доказано.

Утверждение 3. Функция S(N *(Т ),Т ), описываюгцая себестоимости добычи газа, определена, непрерывна и строго убывает от то д о ^ при Т >  0.

Подставим функцию N*(Т ) в функцию (9). Далее продифференцируем функцию S(N*(Т),Т ) по параметру Т и, воспользовавшись соотношением (10), получим

*

(S(N*(Т),Т ))‘ = -kN*(Т)e^-N*^(т)т -----'J-1  < 0.

V V V V, М              V /            <7⁰(1 — _e-N *(т)т )2

Следовательно, функция S(N*(Т ),Т ) строго убывает при Т >  0. Воспользовавшись утверждениями 1 и 2, вычисляем пределы:

^{Z + N (Т} ) hm S⁽N ^(Т), ^Т ) =     (1 — e - N . ₍ т ) т ) = ^то;

♦ к             z + N (Т)       2

lim S(N (1 ),1 ) = k------------- ...... = k—^.

т моо ^{(     (} ), ) _q0(1 — e-N*(т)т )       _q0

Утверждение 3 доказано.

Теперь перейдем к основной части настоящей работы.

3.    Сравнительный анализ себестоимости двух газовых месторождений

Предположим, что имеются два газовых месторождения, из которых необходимо выбрать одно для последующей разработки и добычи газа в течение периода планирования То. Основным критерием выбора для конкурсной комиссии является минимум себестоимости продукции, который определяется на основании предоставленных проектов разработки и обустройства месторождений. Решение конкурсной комиссии является окончательным и пересмотру не подлежит. Выбор конкретного месторождения для осуществления добычи может быть обусловлен и другими причинами. К ним, например, можно отнести возможность подведения газопровода только к одному из двух месторождений.

Очевидно, что в данной ситуации каждый из собственников месторождений желает победить в конкурсе. Поэтому на каждом месторождении с учетом периода планирования То минимизируется себестоимость продукции, что определяет тем самым величину фонда добывающих скважин N *(То). В этой связи ставится естественный вопрос о правильности сделанного выбора: что будет, если вдруг в будущем период планирования изменится с величины То на. другое значение Т?

Тогда возникает следующая задача. На основании имеющихся данных проекты разработок пересчитываются. Если выбор был сделан правильно, то к конкурсной комиссии нет вопросов. Если выбор сделан неправильно, то возникает конфликтная ситуация вплоть до судебных разбирательств.

Таким образом, на основе нового значения периода планирования Т создается новый проект обустройства, в основе которого лежит задача минимизации себестоимости, и определяется другая величина фонда добывающих скважин N*(Т ). Себестоимость в этом случае описывается функцией S (N*(Т),Т ).

Задача 3. Даны пяти положителиных чисел N*(To), Si(N*(То),То), N2*(To'), S 2 (N 2 (To'),To') и То. Первые два числа относятся к первому месторождению, а последующие два числа - ко второму месторождению. Последнее число является периодом планирования добычи газа. Предполагается выполнение неравенства

Si (N* (То), То) <  S 2(W2* ( T o ), То). (17)

Необходимо найти такие значения Т, при которых неравенство

Si(Ni*(T),Т)

выполняется, и такие значения Т, при которых оно не выполняется.

Согласно (12), значения себестоимости рассчитываются по формулам

S.(N*(T),Т) = jT^^)T,     i = 1, 2.

Переменные с индексом i = 1 относятся к первому месторождению, а с индексом i = 2 - ко второму месторождению. На основании исходных данных определяем конкретные значения двух чисел:

Ь. = Si(N*(To),To)Toe^-N, ^(To)To,      i = 1, 2.

Тогда себестоимости вычисляются по формулам

S_t(N* (Т), Т) = Тe^N(T)T,      i = 1, 2.                          (18)

Разделив себестоимости (18) друг на друга, введем обозначение, которое в дальнейшем будем называть отношением себестоимостей R*(Ty.

р        ^S2^(N₂^(T),^T) _ ^Ь2N* (T )T-N* (T )T

^R '     S1(N₁*(T),T)    Ь1^e                 .

Используя новое обозначение, из неравенства (17) получаем ограничение на значение функции R* (Т) в т(>нкс Тд:

1 < В- ^S2^(N2^(Т0⁾,^Т0⁾ _ ^ ^₂*(To)To-^1'(To)To

¹<^{R U}°' = S1(^1■(To),To) = Ьі^e

Перепишем тождество (11) для двух значений z;

e^N(T)T - 1 - _N*(т)т - z.T = 0, i = 1, 2.

Конкретные числовые значения параметров zi и Z2 можно определить из исходных

данных по

формулам z. = eN (T0)T0 — 1 — N-(T0)T0,      i = 1,2.                       (21) T0

Справедливо следующее утверждение.

Утверждение 4. Для каэюдого Т > 0 большему значению z соответствует большее значение N* (Т).

Из тождества (20) при i = 2 вычтем тождество (20) при i = 1. После элементарных преобразований в предположении, что Z2 > zi, приходим к неравенству eV2(T)T - N2 (т)т - eNi(T)T + N*(T)T = (z2 - z1)T > 0.

Учитывая то, что функция e^$ — x возрастает в зависимости от своего положительного аргумента, получаем N2(T)T > N1*(T)T. Отсюда N2*(T) > N^T). Ее.тіі же z₁ > z₂. то N1*(T) > N2* (Т) Утверждение 4 доказано.

Следующее утверждение вытекает из предыдущего.

Утверждение 5. Если N^Tg) < N*(Тд), то N1(T) < N*(T) при Т > 0, и если N₁*(Tg) > N₂*(Tg). пго ^*(Т) > N*(T) щш Т> 0.

Утверждение 6. Функция /(x) = ^^^-у убывает на интервале (0, то) от 1 до 0.

Продифференцируем функцию f (x). В результате получим

/ ‘(х) =

e$(1 — х) — 1 (e^ — 1)2

Знаменатель дроби (22) при ж > 0 положителен. Покажем, что числитель при ж > 0 отрицателен. При ж = 0 числитель дроби (22) равен нулю. Продифференцируем числитель дроби. В результате получаем —жe^ж. Следовательно, на интервале (0, то) числитель дроби (22) и сама дробь отрицательны, т.е. при ж > 0 функция f (ж) убывает. Используя правило Лопиталя, легко найти предельные значения функции f (ж). Утверждение 6 доказано.

Утверждение 7. Функция R*(T) монотонно изменяется на интервале (0, то) от ^ до Она, строго вс нарастает при N^Tq")< N" (То) и строго усбывает при ^(Т_о) > N* (То).

Далее будем исследовать функцию f (Т ) = eN2(T )T -N*(T )T

которая отличается от R* (Т) на постоянную величину. Продифференцируем функцию f (Т):

f ‘(Т) = e^N*^(T)Т-N*^(T)Т[Т(N* (Т)Т)‘ — Т(N1 (Т)Т)']/Т.                (24)

Воспользовавшись равенством (14) и тождествами (20), преобразуем выражение в квадратных скобках соотношения (24):

Т (N₂"(Т )Т)‘ — Т (N1 (Т )Т)‘

22Т          21Т eN( (т)т _ 1   eN*(T)т _ 1

N" (Т )Т     N (Т )Т

- - - . _eN*(T)T _ 1   _eN*(T)T _ 1

Из утверждений 5 и б с учетом соотношений (25) и (24) получаем, что при N" (Т_о) < N"(То) функция (23) строго возрастает, а при N" (Т_о) > N₂ (Т_о) - строго уоы-вает.

Легко показать справедливость следующих пределов:

lim f (Т) = 1;

T -о

lim f (Т) = ²².

T —x       21

Следует отметить, что при поиске значения второго предела в (26) использовались пределы eN*(T)T lim ——— = 2г    г = 1, 2,

T-х Т       г          , , которые можно получить из тождеств (20) и утверждений 1 и 2. Утверждение 7 доказано.

Переформулируем задачу 3 в терминах функции R* (Т).

Задача 3’. В предположении (19) необходимо найти такие значения Т, при которых функция R* (Т) болите 1 и при которых она меньше 1.

Легко показать, что из исходного предположения (19), числовых значений параметров (21), утверждений 4, 5 и 7 вытекает теорема 1, которая является решением задачи 3.

Теорема 1.

Случай 1. Пусти N*(Tо') < ^(То). В этолt случае |2 > 1 zz І^ > 1. тогда:

• а)    функция R* (Т) строго возрастает на интервале (0, то) оіп |2 до ру2-'

• б)    если ^ < 1. то сушуствуст единстве иное положительное число Т". мс: евшее То-такое, что R* (Т) = 1. причем при Т > Т" выполняется неравенство R* (Т) > 1. а при 0 < Т< Т" ^{оно не} выполняется;

• в)    если ¹² > 1 , то неравенство R* (Т) > 1 выполняется при всех положительных значениях Т.

Случай 2. Пусти N"(То) > N^^). В этолi случае |2 < 1 zz |2 > 1. тогда:

• а) функіция R* (Т) строго убывает па интервале (0, то) oiп j² до ^ру²''

ф сели ^2 < 1 . mo cyui,ccmeycm единствеіш,ос положительное число Т*. болъшсс То. такое, что выполняется неравенство К*(Т) = 1, причем при 0 < Т < Т* выполняется неравенство К*(Т) > 1, а при Т > Т* оно не выполняется;

• в) если ^2 > 1, то неравенство Н*(Т) > 1 выполняется при всех положительных значениях Т.

Случай 3. Пусто IV*(То) = N*(То). В этолі случае Ц- = 1 zi |2 > 1. тогда:

• а)    функи,ия П*(Т) на, интервале (0, то) принимает постоямнос знамение. равное |2:

• б)    выполняется неравенство К*(Т) > 1 при всех положителъных значениях Т.

4.    Заключение

В настоящей работе мы рассмотрели непрерывную динамическую модель газового месторождения. В рамках модели были выписаны формулы для расчета прибыли и себестоимости добычи газа. Прибыль считается самым важным экономическим показателем, только прибыль может полностью отражать уровень эффективности деятельности любого предприятия. Однако, в отличие от себестоимости добычи, цена на газ (которая включена в расчеты прибыли) представляет собой слабо прогнозируемое динамическое значение. Этот факт значительно усложняет прогноз совокупной прибыли. Себестоимость определяется как отношение капитальных затрат при строительстве месторождения к объему природного газа, добываемого в плановый период. Капитальные затраты описываются как линейная функция одной переменной с постоянной и переменной частями, причем переменная часть определяется фондом добывающих скважин.

Совокупная величина добычи газа зависит от величины горизонта планирования. Для каждого значения горизонта планирования мы находим минимальную себестоимость добычи газа и однозначно определяем стоимость фонда добывающих скважин. Было доказано, что оптимальное значение фонда добывающих скважин с изменением горизонта планирования строго убывает от бесконечности до нуля. При этом минимальное значение себестоимости добычи газа строго убывает от бесконечности до некоторого положительного значения. Эти свойства фонда добывающих скважин и себестоимости добычи газа не противоречат основному свойству модели - в течение бесконечного времени весь запас природного газа может быть полностью извлечен одной скважиной.

Полученные результаты позволяют принимать правильные решения в следующей ситуации. В конкурсе на разработку участвуют два месторождения; для разработки выбирается одно их них с наименьшей себестоимостью добычи газа, причем пересмотр выбора невозможен. В дальнейшем период планирования изменяется, происходит перерасчет себестоимостей и других показателей для каждого месторождения. Возникает вопрос: правильным ли был сделанный выбор? В случае отрицательного ответа возникает конфликтная ситуация со всеми вытекающими последствиями.