Secure Mobile Agent Migration Using Lagrange Interpolation and Fast Fourier Transformation
Автор: Pradeep Kumar, Niraj Singhal, Dhiraj Pandey, Avimanyou Vatsa
Журнал: International Journal of Computer Network and Information Security @ijcnis
Статья в выпуске: 4 vol.15, 2023 года.
Бесплатный доступ
Mobile agent is a processing unit works on the behalf of host computer. Mobile agent with intelligence provides a new computing prototype that is totally different from conventional prototype. Mobile agents are automatically itinerating from one host Computer to another host computer and execute assigned task on the behalf of user in heterogeneous environment under own control. Because mobile agents roam around distributed networks automatically, the security of the agents and platforms is a major concern. The number of mobile agents-based software applications has increased dramatically over the past year. It has also enhanced the security risks associated with such applications. Most protection systems in the mobile agent paradigm focus on platform security and provide few guidelines for mobile agent security, which is still a challenging topic. There is a risk to information carries by mobile agents from the malicious mobile agents who can modify and steal the confidential information. In this paper proposed multilevel authentication framework of mobile agents and platform based on Lagrange interpolation and fast Fourier transformation (LIFFT). In this frame work ‘n’ number of mobile agent have two level of security first level key used authentication and second level of key used for execution of mobile agents.
Mobile Agents (MA), Complex Number, Lagrange Interpolation, DFT, Butterfly Network, Fast Fourier Transform
Короткий адрес: https://sciup.org/15018635
IDR: 15018635 | DOI: 10.5815/ijcnis.2023.04.07
Текст научной статьи Secure Mobile Agent Migration Using Lagrange Interpolation and Fast Fourier Transformation
Mobile agent Mobile agent [1] is smart active process dynamically moving from one site to another site also communicates among intermediate agents. Each and every mobile agent has own code, state and data. Here prime concern to provide security of mobile agent’s code, state and data during communication. Mobile agent transfers the code (data+ thread +authentication of owner)[2].
Mobile agent has three main attributes.
Mobile Code: Mobile code defines the mobile agent behavior in any particular languages.
Sate: Mobile sate define the state of mobile agent.
Attributes: Information about the mobile agent like source address destination address, history of mobile agent, authentication related data etc.
To design Frame work based on the mobile agent technology [3] is the amendment of distributing computing. A Mobile agent completes the assigned task on another platform on the behalf of owner. Mobile agent technology provides high degree of adaptability [4] in computing. There are three primary classifications of computing.
-
• Client server computing: In client-server processing [5] a server offers types of assistance to client.
-
• Code on demand Computing: In code on demand processing service provider sends executable program from a server provider to a user on the solicitation from the user side.
-
• Agent Based computing: Mobile agent paradigm [6] work on bases of mobile agent life cycle and works on the bases of owner in heterogeneous environment. Mobile agent computing shown in figure 1.
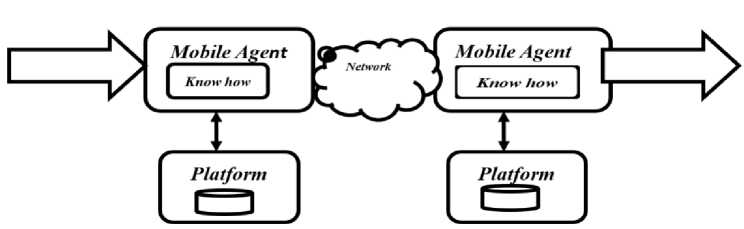
Fig.1. Mobile Agent computing
In client sever methodology data moves starting with one client then onto the next however the development of information takes more bandwidth capacity of channel. In the Mobile agents approach rather than transferring of data agents moves one host to another host to execute assigned works takes less bandwidth.
Mobile agent paradigm uses a life cycle [7] during the transaction of agent and platform shown in fig 2.
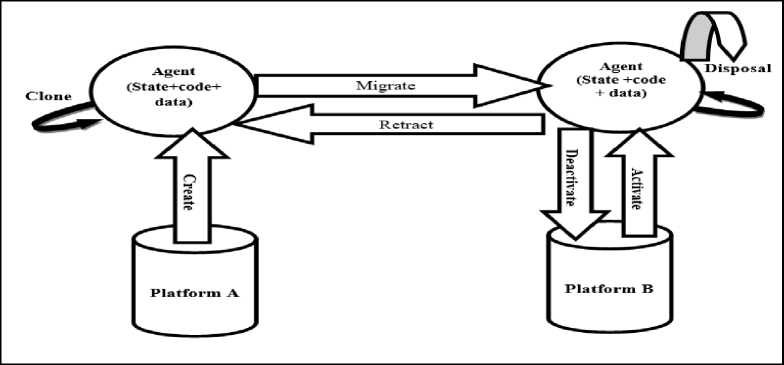
Fig.2. Mobile Agent life cycle
-
• Creation: A newly agent is creating and initialized state of agent.
-
• Cloning: A duplicate mobile agent is created.
-
• Dispatch: An agent dispatch and communicate to agent and platform.
-
• Deactivation: In Deactivation phase agent is in sleep state save in to memory.
-
• Activation: An agent is activated from the memory.
-
• Retraction: In this phase an agent is ready to execute operation.
-
• Communication: Communication occur among agent and host
-
• Disposal: In the final sate a mobile agent terminated after completion of process.
Necessity of Security in Mobile Agent Based Framework
Mobile agents are migrating automatically in malicious environment in open network. So, to provide the protection of mobile agents is a crucial issue for mobile agent’s paradigm. There are different parameters of security which are shown in figure 3.
Confidentiality: In any developed frameworks, confidentiality should not be compromised during communications either by hoped agents or by different platforms under execution of agent process.
Data integrity: Data and information should be in original form not tampered by any third party. The integrity needs to maintain for any secure operation of mobile agents, both local as well as other platforms on which agent moves for execution.
Availability: Availability means data and information are required by platform or agents should be available. The agent platform will make it available to both local and remote agents.
Apart from above mentioned parameters, verification [8] of mobile agents and platform is also required. The crucial issue to developed mobile agent-based framework [9] is protection of mobile agents during the relocation in distributed computing. In the past created mobile agent frameworks, the greater part of the focus was on choosing the working of mobile agents instead of security. Some mobile agent framework introduces the security but there is absence of implementation in real time. Some major issues arise related to attacks on mobile agent models. Mobile agent Security classified in to three main areas
• Security of Mobile agent
• Security of Platform
• Security of mobile agent Network
2. Related Works
There is a requirement of a safe mobile agent framework [10] to support secure transaction among mobile agents and platform. In this propose article, a secure key administration scheme of mobile agent paradigm has been proposed based on the Shamir secret share [11]and fast Fourier transformation.
The whole structure of paper is as follows. In Sect. 2 introduce related work about the secret sharing scheme and in Sect3, discuss about the problem statement. Problem statement discuss in Sec 3. Some fundamental definitions related to proposed scheme with preliminaries focused in Sect. 4. Some security measures discuss in Sect.5. The performance of framework compared with other scheme discussed in Sect. 5, and finally in Sect. 7 conclusions and future work has been focused.
Disclosure of information, denial of service, and corruption of information are the main classes of threats to security. In Several ways, we can examine these classes of threats in greater detail as they apply to agent framework. Mobile agents simply offer a greater opportunity for abuse and misuse, broadening the scale of threats significantly.
Xiangru Liu et al. [12] proposed a multilevel authentication scheme based on threshold secret sharing and singular value decomposition ghost imaging. The role of using (t, n) threshold secret distribution makes the multilevel verification possible and the SVD algorithm makes faster recreation of secret.
Jing Li et al . [13] designed a multi-secret sharing mechanism using multi-target MSP. There is no requirement of authentication centre and each participant has authority to generate secret . So, the mechanism can apply for decentralized computing . On the bases of multi-target MSP, design a multi-role e-voting model by using Chinese Remainder Theorem (CRT). Lein Harn et al . [14] proposed the multilevel threshold secret key distribution by using CRT algorithm. This scheme secures like as Asmuth–Bloom’s SS . In the proposed model participant are divide into different security level and each level participants have different value of threshold. The secret can reconstruct only if sufficient number of athecate shareholder are available. , Share are in the top-level subset can be at lower level of subset to reconstruct secret. Special property of MTSS is that each participant has only one secret share.
Hao Hua et al. [15] proposed a multi-level security scheme based on Region incrementing VC scheme (RIVCS). The performances of proposed scheme are better in terms of lossless recovery and efficiency. Proposed scheme is feasibility and flexibility. Constantin Catalin Dragan et al .[16] proposed a distributive weighted threshold secret distribution mechanism by using updating of Asmuth–Bloom threshold scheme . The main advantage of this scheme is perfect zero-knowledge and asymptotically perfect . Yi-Ning Liu et al . [17] proposed, a modified (t, r, n)-hierarchical multilevel image recovery protocol by using Lagrange interpolation and threshed value. We can access the image at multilevel using threshold value. In the proposed mechanism, each share of image has equal role to recover of original image at multilevel.
Xianye Li et al. [18] proposed a hierarchy based multilevel authentication model for multiple-image by using vector operation. By using the vector operation grayscale image split in to ‘n’ part of shadow image key and distribute to n shareholders. High-level and low-level authentication of binary image and grayscale image are accomplished in this scheme. For high level and low-level authentication require large number of shadow image and a smaller number of shadow images respectively. Hefeng Chen et al. [19]propose a new secret reconstruction scheme based on threshold value and Euler theorem. The proposed scheme has better performance as compare to other threshold based secret sharing scheme. Abdul Basit et al. [20] proposed a Hierarchy based multilevel multi secret sharing scheme by using polynomials equation and one-side function. The security scheme depends on the one side computation complexity of function. In this mechanism, shareholders are divided into different level based on Hierarchy. In hierarchy each level has to assign a different threshold value. A special feature of scheme is reusability of share. So, there is no need to update the share for next transaction. Only authorized shareholders can reconstruct the secret key and low level of shareholder can be used to reconstruct share in high level. Om Prakash Verma et al. [21] proposed a hybrid-based Visual secret sharing scheme to share multiple secrets in a multistage computing. In this approach distribute multiple secrets keys at different stage. The proposed scheme faster than previous scheme. Randomness of key provides higher security. Proposed model works efficiently work in an environment where agents and participant are not reliable and also when they are not commonly trusted.
Chadha Zrar et al. [22]design security mechanism aspects at the hour of the transaction between a mobile agent and a stationary agent. In MA-UML integrate new extension to provide the higher level of security. In this paper discuss about mobile agents related attack and threat such as integrity, non-repudiation and availability. Dina Shehada et al. [23] presented a new Broadcast based Secure Mobile Agent scheme for distributed computing. The proposed approach is using combination of symmetric and asymmetric cryptography with broadcast architecture of mobile agents to generate higher level of security and better performance of distrusting applications. Adri Jovin John Joseph et al . [24] presented significant commitment of this work is the presentation of Trust Score, a novel measure for evaluating the dependability of a stage and Trust Score based Itinerary arranging Algorithm, which helps the Mobile Agent in dynamic dependent on Trust Score. The Trust Scoring framework is improved by methods for presenting Trust ability Co-productive of Variation. The Trust Scoring framework delivers various sections for a similar worker stage, yet this framework binds together the numerous passages utilizing the Co-productive of Variation of the sections which are brought together as another measure, Trust ability Co-proficient of Variation. In view of the Trust ability Coefficient of Variation, the positioning is accomplished for the worker stages. In light of exploratory outcomes, it is discovered that the proposed Trust Ranking framework is better contrasted with that of the other existing choice emotionally supportive networks of that sort.
Yan-Xiao Liu et al. [25] proposed a solid (n, t, n) VSS to check the solid t consistency of secret share. This proposed conspire is more productive than Harn and Lin's solid (n, t, n) VSS. In Harn and Lin's VSS, participants need to use 100 confirmation polynomials to check the solid t-consistency of expert key. In our VSS, participants use the sub-polynomials of expert key to develop a check polynomial and use them to confirm key. Also, we propose a productive (n, t, n) MSS to permit participants to share (n - t + 1) insider facts safely. The proposed (n, t, n) MSS is adjusted to turn into a (n, t, n) VMSS with obvious component. The security of all proposed plans is unequivocally secure. Priyanka Singh et al. [26] Purposed a scheme for diminishing the defenselessness of delicate media data living over disseminated cloud server farms oversaw by outsider participant, a safe SVD-FrFT based watermarking plan for encoded space has been proposed in this paper. Provide the security for sensitive data by using multiple Shamir shares. Secret data was inserted into a portion of its arbitrary looking shares to demonstrate the legitimate responsibility for content on the recipient end. The power of the plan was tried against various attacks conceivable by the hackers once the data is rethought at the cloud. The plan could even endure the situations where a portion of the cloud servers completely go down and was discovered to perform agreeably well against various attack situations in encoded space itself. The regeneration of the media likewise stayed unaffected except if more than n - к shares were assaulted at the same time.
Byomakesh Mahapatra et al. [27] discussed about growth of cellular IoT paradigm along with the mobile and wireless scheme for significant distance information transmission leads to more challenging security issues. The LTE based C-IoT is an idea utilized for the long-range IoT application. In this paper, we have presented another ML-AKA security convention for the three-layer shared validation in a C-IoT framework. For D2D confirmation in ML-AKA, an improved symmetric key cryptography method is utilized, which give greater adaptability in term of D2D or D2X verification in a C-IoT organization. The proposed ML-AKA convention more productive regarding execution time and verification time delay. Massimo Giuliett et al. [28] proposed a methods from projective spaces over limited fields, a development of ideal 1-mathematical secret sharing plans for three-level access structures has been introduced. From the computational perspective, a significant element is that express formulae for the development of the offers are given. Keju Meng et al. [29] proposed a multiple level secret sharing (MLSS) more adaptable and mainstream in application, the paper presents first the thought of multi-bunch threshold secret sharing (MGSS), which permits a shareholder of one gathering to partake covertly remaking in another gathering without hierarchical limit. Proposed scheme based on the Chinese remainder theorem (CRT). In the plan, a shareholder may take an interest stealthily remaking in different gatherings while it keeps just one secret share. Also, when adequate number of participants team up to regenerate the secret in a group, they first structure a tightly coupled subgroup by creating a randomized segment with the share, to such an extent that the secret can be recreated just if all participants have substantial shares in the group and really take an interest secret recreation. Along these lines, the proposed tightly coupled MGSS conspire isn't simply impervious to IP and SC attacks yet additionally more adaptable and famous in applications.
3. Problem Statement
Mobile agents using the resources of other platform at the time of execution of process during life cycle of mobile agents shown in fig 2. Secure execution of task totally dependent on the security of other platform and malicious mobile interact during the migration of mobile agents. So mobile agents and platform are open for attack. There is a requirement to design such type of mechanism that provides security during communication as well as at the hour of exaction. Protection of mobile agents and platform is prime concern in distributing computing. There are many cryptographic algorithms can use for the authentication of mobile agents and platform but the security of conventional cryptographic scheme based on the security [30] of key using for encryption and decryption. Security [31] of mobile agents and platform is completely based on strength of a key which is using for execution and authentication. Security of mobile agent and resources of host is major problem in mobile agent paradigm. For the migration of mobile agent, we require completely trustworthy environment but maintain trust on another agent and other host is not possible.
A new scheme multilevel authentication of mobile agents and host resources is based on Lagrange interpolation [32] and fast Fourier transformation [33] proposed.
4. Proposed Solution
Preliminaries
The basic preliminaries used in this paper have been discussed here such as, Shamir’s scheme, Lagrange’s Interpolation complex number, discrete Fourier transformation, butterfly permutation, and fast Fourier transformation. Lagrange’s Interpolation and fast Fourier transformation has been used to provide multilevel authentication of mobile agents and platform.
Shamir’s Secret Sharing: Let us consider β 0 , β 1 , β 2, ……….. β k-1 ∈ GF (p)F(x) = (β 0 x0+ β 1 x1 + β 2 x2 +................+
F(x) = XiVi П ,j., ^ х X
X l X j
Since f (0) = β 0 = S, the secret key evalute using
Secretkey (S) = Z^ Pi^i
Where p i = П ,< j</v,,^,-— jy
X J X l
Secret share is genrated by using t partial share by using F(0) = β 0 modp
Complex Number: A complex number is collection of real number and imagi n ary number which is in the form of Z=A+jB. A is real part and B are imaginary part in complex number. Where ^J = -1 Modulus of complex number represented as |z| = 7л 2 + в 2 .
Discrete Fourier transform (DFT) used in digital signal processing to covert time domain to frequency-domain. In the security of information input covert in to another domain, our aim converting one sequence of input in to different sequence of complex number output. DFT of n input sequence n=0, 1, 2, 3, 4……….N-1 represented as given equation
X (k) = Z n=1 x(n)e -j“ k=0, 1, 2, 3, 4N-1 (3)
X (k) also represent by using matrix
IDFT formula
X (k) = [ 1
. 2лк .2TTkn e-j-N" e-7 n
%0
_ . 2лк(М-1)
e 7 n ]= xl
LxN - 1J
x (n)= 1Z:
W-1
■ k=0
. 2Як
X(k)ejxr
w n = e -
. 2П ' J"N
So,
X (k) = Z " - 1 x(n) (^n) k k=0, 1,2, 3,4.........N-1
|
Г X(0) 1 |
'1 |
1 |
1 , 9 |
1 12 12 3 |
1 1 |
г %(0)-| |
||
|
X(1) |
W n |
W „ |
W^ ...... |
W £ 1 |
x(1) |
|||
|
X(2) |
1 |
W 2 |
W „ |
w „ |
W „ 2(2-1) |
x(2) |
||
|
X(3) ■ |
= |
1 ■ |
W |
W 6 |
9 *' П ■ 2 12
|
W „ 3(N-1) "' |
, (3) ■" |
|
|
■ Lx(N - 1)J |
■" L1 |
r V |
w „ 2('v-1) |
w 3 ( W —1) r Г ^^ ■ ■ ■ ■ ■ ■ |
■■ wr1)(N-1) . |
■ Lxj v-1 J |
Butterfly permutation: Butterfly permutation also known as bit reversal permutation. Butterfly permutation defined as, β(x) (a k , a k-1 ... a 2 , a 1 ) = {a 1 , a k-1 ... a 2 , a k }
Fast Fourier Transform FFT is the fastest way to calculate DFT and IDFT. By using the FFT in number of inputs is n reduces the time complexity from O (n2) to O(nlogn). FFT is the fastest way for computation. Fast Fourier transformation based on the divide conquers technique. There are many applications of FFT like fast polynomial multiplication, fast matrix vector multiplication, filtering algorithm etc.
Proposed Scheme for Security of Mobile Agent and Platform: Security of mobile agents and platform based on the vigorous multilevel key generation scheme proposed here shown in figure 3. Security of proposed scheme based on the threshold value decided by owner and divide secret key in ‘n’ partial share of mobile agents and double level of security key using one for authentication of mobile agent and platform other for execution of assigned task by owner. For the security of agent-based applications a new scheme based on the Lagrange interpolation and fast Fourier transformation proposed here. In the proposed framework security key of execution divided among n mobile agents using t degree polynomial shown in algorithm 1, (i, S i ) 0≤ i ≤n at first level. At the second level by applying fast Fourier transformation covert these partial shares in the form of complex number (Z i =x i +y i ) and select random value for authentication of mobile agents, by using algorithm 2 generate public parameter (p 1 , n) and broadcast to different number of hosts.
Platforms at which mobile agent want to execute their task for authentication of mobile agents apply algorithm 4, IFFT (Z) to generate authentication key. After generating authentication key apply algorithm 5, to generate execution key by applying Lagrange interpolation.
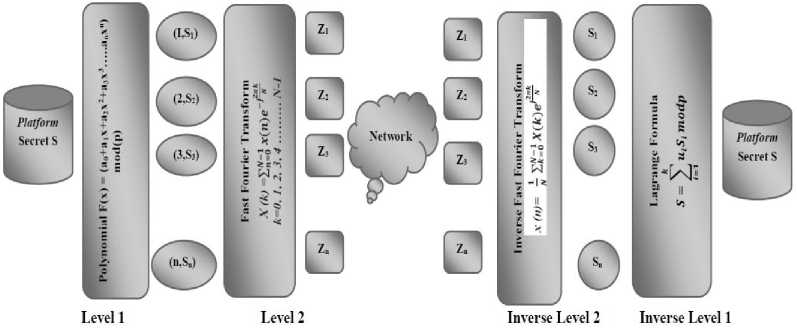
Fig.3. LIFFT Frame work for secure migration of mobile agent
Algorithm: Algorithm of proposed mathematical model categorized in to main three parts initialization, share creation and reconstruction of share.
Lifft Algorithm
Algorithm 1: Generation of partial secret at level 1using Lagrange polynomial
-
1. Consider the Lagrange polynomial of degree n =t-1 , F(x) = (a 0 +a 1 x+a 2 x 2 +a 3 x 3 +a 4 x 4 ……………………..a n x n ) modp, p is large prime number and a 1 , a 2 …, and a k-1 are arbitrarily real number chosen from from Z/PZ.
-
2. Consider Execution secret F (0) =S.
-
3. By using polynomial generate(i , S i ) , 0≤ i ≤n /* Generate n partial share*/
/* i is the mobile agent identity */
Algorithm 2: Generation of partial secret at level 2 fast Fourier transform (FFT) Fast Fourier Transforms ( S i )
|
is a power of 2*/ |
|
root of unity*/ |
|
|
|
|
|
/* since -ro ^ = ro ' +n/2 |
|
/• ro ^ iterativeiy*/ |
|
Caicuiate pubiic parameter p1= (S ievei 2 + Е П—0 1 xt 15. Broadcast (p 1 ,N) |
)/(Z n—o 1 y t )+4 |
/* Z i =x i + y i * /
Algorithm 3: Secret regeneration at level 2 Inverse Fast Fourier transforms IFFT (Z)
-
1. Level 2 secret generated by S ievei 2 = p i*( (2 ”=0 1 Vt )+4 )- ЭД —о x t )
-
2. For k=0, 1, 2, 3, 4 ……… N-1
-
3. Sim ^Х^Т /*0, 1, 2, 3, 4N-1*/
-
4. Return Z
Algorithm 4: Secret regeneration at level 1 Inverse Laplace transforms (ILT) x—s
-
1. F(x)= £L.S t \i^!; , r,^modp
-
2. Lagrange interpolation Since f (0) = a0 = S, the shared secret can be expressed as
-
3. S = S '=1 utSt modp
s i —s у
Where
ut =
П
1 (Х-Sj) (Sj-St) by using F(0)=a0modp=S /*Execution hey of mobile agents.*/ Case 1: Now we are considering number of users is power of 2. Let us consider prime number p=23 and secret share S=17 host create n =8 mobile agents ma1, ma2, ma3, ma4, ma5,ma6,ma7,ma8, each mobile agents have unique id 1,2 ,3 ,4 ,5 ,6 ,7 ,8 respectively. On the basis of mobile agents’ ids Host create 8 partial keys based on Lagrange polynomial F(x) = (a0+a1x+a2x2+a3x3+a4x4……………………..anxn) mod p Here threshold value t=6. So degree of polynomial is 5. F(x) = 12x^5 + 18x^4 + 9x^3 + 20x^2 + 34x^1 + 40 mod23 Select any random value of level 2 secret Slevel 2 = 745791.0 Calculate public parameter pi= (S level 2 +S”=—O Xt )/ (E!=u Vt ) +4 /* Zi =Xi + Xi */ P1 = 5039.1824324324325 Broadcast (5039.1824324324325, 8) to every mobile agent. This is public parameter. At the receiver end calculate authentication secret using Sievei 2 = pi^SSo Xi )+4 )- S^-0 Xi ) /* Zi =Xi + У/ */ Slevel 2=745791.0 After applying IFFT and Inverse Lagrange interpolation generate secret key for execution in Lagrange interpolation threshold value is 6, now randomly choose six partial shares generated by inverse Lagrange interpolation by using F(0)=a0modp=S=17 . Table 1. Share generation by lagrange polynomial and fourier transformation Secret Share f(x) F(x) = 12x^5 + 18x^4 + 9x^3 + 20x^2 + 34x^1 + 40 mod23 Shares at level 1 Shares at level 2 by FFT S1 F (1) share generation 1 =( 1 , 18 ) 107.-0.j S2 F (2) share generation 2 =( 2 , 12 ) 10.70710678+9.77817459j S3 F (3) share generation 3 =( 3 , 17 ) -10. -13.j S4 F (4) share generation 4 =( 4 , 5 ) 9.29289322 +5.77817459j S5 F (5) share generation 5 = (5, 8) 17. -0.j S6 F (6) share generation 6 =( 6 , 17 ) 9.29289322 -5.77817459j S7 F (7) share generation 7 =( 7 , 19 ) -10. +13.j S8 F (8) share generation 8 =( 8 , 11 ) 10.70710678-9.77817459j
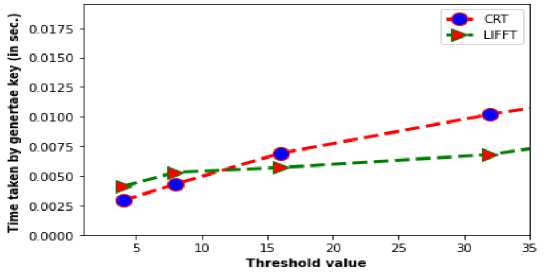
5. Security Measurements • Validity (V): Scheme is said to be valid if secrets reconstructed by host computer using threshold number of secret. Lagrange Interpolation provides more validity to scheme. Randomly choose t valid share can reconstruct secret. • Traceable (T): Any scheme is said to be traceable if we identify whether the given shareholder to reconstruction of secret is authenticate or not. • Confidentiality (C): Any algorithm is said to be confidential if less than t shareholder cannot reveal the secret. • Consistency (C): Any scheme provides consistency if any set of t share out of n valid share generate same secret. LIFFT algorithm is consistency because of Lagrange interpolation and Fourier transformation. Table 2. Comparison by using security parameter S. No Scheme Name Year V C C T 1 A new efficient (t, n) verifiable multi-secret sharing (VMSS) based on YCH scheme 2005 yes yes No yes 2 A practical verifiable multi-secret sharing scheme 2007 yes yes No yes 3 An efficient threshold verifiable multi-secret sharing 2008 yes yes No yes 4 An efficient multi-use multi-secret sharing scheme based on hash function 2010 yes yes No yes 5 Multilevel threshold secret sharing based on the Chinese remainder theorem 2014 yes yes No yes 6 Efficient verifiable multi-secret sharing scheme based on hash function 2014 yes yes Yes yes 7 Dealer-leakage resilient verifiable secret sharing 2014 yes yes No yes 8 A Hybrid-Based Verifiable Secret Sharing Scheme Using Chinese Remainder Theorem 2019 yes yes yes yes 9 Proposed (LIFFT) - yes yes yes yes The proposed mechanism based on Lagrange interpolation and fast Fourier transformation implemented in python platform. Here we are comparing our proposed multilevel framework with Chinese remainder theorem based secret key generation for mobile agent platform. Table 3 and table 4 represents the response time taken to generate and reconstruct secret key for different number of 10 different result for every value of mobile agent shown in Table 3, n=4, 8,16,32,64. It is observed that CRT generates only single level of authentication but LIFFT approach provides double level of authentication. From the experiment response time of initialization, distribution and regeneration of secret key at two levels is quite low as compare to CRT scheme security at single level in both cases average case and best case. Yellow color shown in tables represents result in best case. Average case evaluated on the bases of ten different observations. In LIFFT frame work ‘n’ number of partial shares created on the basis of Lagrange polynomial at fist level and, at second level we are using fast furrier transformation to create share. At the execution platform both algorithms apply in reverse order to decode authentication and execution key of mobile agents. Graph shown in figure 4 represents the performance comparison between CRT and LIFFT in average case. After analysis of graph, it is found that LIFFT response time is very less as compare to CRT. Graph shown in figure 5 represents the performance comparison between CRT and LIFFT in Best. After analysis of graph, it is found that LIFFT response time is very less as compare to CRT. Table 3. Time taken versus number of mobile Agent for CRT CRT n 4 8 16 32 64 1 0.0060 0.0069 0.0074 0.0122 0.0216 2 0.0055 0.0065 0.0086 0.0128 0.0229 3 0.0053 0.0071 0.0082 0.0124 0.0160 4 0.0043 0.0070 0.0069 0.0102 0.0236 5 0.0029 0.0043 0.0080 0.0148 0.0168 6 0.0053 0.0077 0.0088 0.0138 0.0243 7 0.0040 0.0066 0.0086 0.0134 0.0208 8 0.0041 0.0048 0.0076 0.0164 0.0156 9 0.0058 0.0053 0.0102 0.0129 0.0263 10 0.0071 0.0069 0.0100 0.0134 0.0215 Avg 0.0050 0.0063 0.0084 0.0132 0.0209 Table 4. Time taken versus number of mobile Agent for LIFFT LIFFT 4 8 16 32 64 1 0.0052 0.0062 0.0071 0.0068 0.0153 2 0.0059 0.0064 0.0069 0.0084 0.0125 3 0.0056 0.0058 0.0079 0.0096 0.0120 4 0.0041 0.0059 0.0070 0.0099 0.0145 5 0.0051 0.0053 0.0064 0.0081 0.0127 6 0.0052 0.0053 0.0075 0.0070 0.0109 7 0.0048 0.0063 0.0077 0.0090 0.0147 8 0.0053 0.0066 0.0057 0.0097 0.0138 9 0.0048 0.0085 0.0080 0.0100 0.0148 10 0.0050 0.0078 0.0068 0.0083 0.0201 Avg 0.0051 0.0064 0.0071 0.0087 0.0141 Fig.4. No of Mobile agents versus time in average case Performance Comparison on SSS After the analysis of Proposed multilevel security framework based on the LaGrange interpolation and fast Fourier transformation with CRT based security further compare with another mechanism with different parameter access structure, multi secret, exponential computation and changeable threshold value. Table 5. Shown the comparison of proposed approach with given thee approach Strong (n,t,n) scheme, Efficient (n, t, n) scheme and CRT Based secret sharing . Proposed approach provides multilevel security of mobile agent with changeable threshold value for different transaction. Also, it will take less computational time as compare to other. THRESHOLD Vs TIME BEST CASE Fig.5. No of mobile agents versus time in best case Table 5. Performance comparison of secret sharing scheme Parameter Strong (n,t,n) scheme Efficient (n, t, n) scheme CRT Based LIFFT Access Structure Single level Single level Single level Multilevel Multi-Secret No No No YES Exponential Computation No No Yes No Changeable Threshold No No No Yes
7. Conclusions and Future Scope The plan of security for mobile agents during the correspondence of mobile agents between various hosts is as yet an urgent issue. In this paper proposed a multilevel authentication of mobile agents and platform using Lagrange interpolation and fast Fourier transformation to ensure the security at multiple levels. As we are using multiple level securities create confusion for malicious mobile agent. This new methodology gives the protection of key security utilizing threshold value and a vigorous key administration scheme. This methodology assists with observing the security of access of mobile agents just to real number of users. Validation of any mobile agents by different platform is important part of security. The proposed framework of mobile agents expands the security of key at multilevel one for authentication and other use for execution of assigned task. By experiment show that our scheme takes less computational time as compare to CRT based scheme algorithm and provide security at multilevel. Proposed approach is approx. 10% faster than the CRT based single level authentication. In future work, design such type of framework the also identify the malicious agents in untrusted environments. This would help the mobile agents as well as platform from cheating by malicious agents.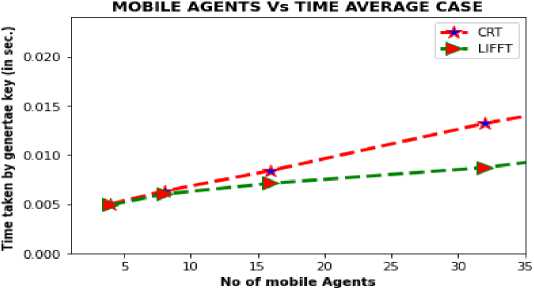
Список литературы Secure Mobile Agent Migration Using Lagrange Interpolation and Fast Fourier Transformation
- P. Kumar and D. Aggarwal, “Software Mobile Agent Migration : A Review,” vol. 6, no. 4, pp. 25–32, 2019.
- R. Qayyum and H. Ejaz, “Data security in mobile cloud computing: A state of the art review,” Int. J. Mod. Educ. Comput. Sci., vol. 12, no. 2, pp. 30–35, 2020, doi: 10.5815/ijmecs.2020.02.04.
- U. Upadhyay, P. Kumar, and D. Aggarwal, “Secure migration of mobile agent using AES & secret sharing approach,” Int. J. Emerg. Technol., vol. 10, no. 2, pp. 150–155, 2019.
- P. Sharma and P. Kumar, “Review of Various Image Steganography and Steganalysis Techniques,” Int. J. Adv. Res. Comput. Sci. Softw. Eng., vol. 6, no. 7, pp. 152–159, 2016.
- M. Kaur and S. Saxena, “A review of security techniques for mobile agents,” Proceeding - IEEE Int. Conf. Comput. Commun. Autom. ICCCA 2017, vol. 2017-Janua, pp. 807–812, 2017, doi: 10.1109/CCAA.2017.8229906.
- M. Alruqi, L. Hsairi, and A. Eshmawi, Secure mobile agents for patient status telemonitoring using blockchain, vol. 1, no. 1. Association for Computing Machinery, 2020.
- P. Bagga and R. Hans, “Mobile Agents System Security,” ACM Comput. Surv., vol. 50, no. 5, pp. 1–45, 2017, doi: 10.1145/3095797.
- R. Nur Hadisukmana, “An Approach of Securing Data using Combined Cryptography and Steganography,” Int. J. Math. Sci. Comput., vol. 6, no. 1, pp. 1–9, 2020, doi: 10.5815/ijmsc.2020.01.01.
- D. K. Singh, M. Ashraf, and R. K. Rai, “A modified security architecture for mobile agent based creeper,” Int. J. Adv. Sci. Technol., vol. 29, no. 1, pp. 748–752, 2020.
- Z. chaouch and M. Tamali, “A Mobile Agent-Based Technique for Medical Monitoring (Supports of Patients with Diabetes),” Int. J. Comput. Models Algorithms Med., vol. 3, no. 4, pp. 17–32, 2012.
- S. Sabitha, “International Journal of Emerging Technologies in Computational and Applied Sciences ( IJETCAS ),” Int. J. Emerg. Technol. Comput. Appl. Sci. ( IJETCAS ), pp. 513–519, 2013.
- X. Liu et al., “Optical multilevel authentication based on singular value decomposition ghost imaging and secret sharing cryptography,” Opt. Lasers Eng., vol. 137, no. September 2020, 2021, doi: 10.1016/j.optlaseng.2020.106370.
- J. Li, X. Wang, Z. Huang, L. Wang, and Y. Xiang, “Multi-level multi-secret sharing scheme for decentralized e-voting in cloud computing,” J. Parallel Distrib. Comput., vol. 130, pp. 91–97, 2019, doi: 10.1016/j.jpdc.2019.04.003.
- L. Harn, Z. Xia, C. Hsu, and Y. Liu, “Secret sharing with secure secret reconstruction,” Inf. Sci. (Ny)., vol. 519, pp. 1–8, 2020, doi: 10.1016/j.ins.2020.01.038.
- H. Hua, Y. Liu, Y. Wang, D. Chang, and Q. Leng, “Visual cryptography based multilevel protection scheme for visualization of network security situation,” Procedia Comput. Sci., vol. 131, pp. 204–212, 2018, doi: 10.1016/j.procs.2018.04.204.
- X. Jia, D. Wang, D. Nie, X. Luo, and J. Z. Sun, “A new threshold changeable secret sharing scheme based on the Chinese Remainder Theorem,” Inf. Sci. (Ny)., vol. 473, pp. 13–30, 2019, doi: 10.1016/j.ins.2018.09.024.
- Y. N. Liu and Z. Wu, “An improved threshold multi-level image recovery scheme,” J. Inf. Secur. Appl., vol. 40, pp. 166–172, 2018, doi: 10.1016/j.jisa.2018.03.009.
- X. Li et al., “Hierarchical multilevel authentication system for multiple-image based on phase retrieval and basic vector operations,” Opt. Lasers Eng., vol. 89, pp. 59–71, 2016, doi: 10.1016/j.optlaseng.2016.04.021.
- H. Chen and C. C. Chang, “A Novel (t,n) Secret Sharing Scheme Based upon Euler’s Theorem,” Secur. Commun. Networks, vol. 2019, no. c, 2019, doi: 10.1155/2019/2387358.
- A. Basit, N. C. Kumar, V. C. Venkaiah, S. A. Moiz, A. N. Tentu, and W. Naik, “Multi-stage multi-secret sharing scheme for hierarchical access structure,” Proceeding - IEEE Int. Conf. Comput. Commun. Autom. ICCCA 2017, vol. 2017-Janua, pp. 557–563, 2017, doi: 10.1109/CCAA.2017.8229863.
- O. P. Verma, N. Jain, and S. K. Pal, “A Hybrid-Based Verifiable Secret Sharing Scheme Using Chinese Remainder Theorem,” Arab. J. Sci. Eng., vol. 45, no. 4, pp. 2395–2406, 2020, doi: 10.1007/s13369-019-03992-7.
- C. Zrari, H. Hachicha, and K. Ghedira, “Agent’s security during communication in mobile agents system,” Procedia Comput. Sci., vol. 60, no. 1, pp. 17–26, 2015, doi: 10.1016/j.procs.2015.08.100.
- D. Shehada et al., “BROSMAP: A novel broadcast based secure mobile agent protocol for distributed service applications,” Secur. Commun. Networks, vol. 2017, pp. 13–15, 2017, doi: 10.1155/2017/3606424.
- A. J. John Joseph and M. Mariappan, “A novel trust-scoring system using trustability co-efficient of variation for identification of secure agent platforms,” PLoS One, vol. 13, no. 8, pp. 1–19, 2018, doi: 10.1371/journal.pone.0201600.
- F. Casino, T. K. Dasaklis, and C. Patsakis, “A systematic literature review of blockchain-based applications: Current status, classification and open issues,” Telemat. Informatics, vol. 36, no. May 2018, pp. 55–81, 2019, doi: 10.1016/j.tele.2018.11.006.
- P. Singh, B. Raman, and M. Misra, “A secure image sharing scheme based on SVD and Fractional Fourier Transform,” Signal Process. Image Commun., vol. 57, no. December 2016, pp. 46–59, 2017, doi: 10.1016/j.image.2017.04.012.
- B. Mahapatra, A. K. Turuk, A. Nayyar, and K. S. Sahoo, “Jou rna,” Microprocess. Microsyst., p. 103720, 2021, doi: 10.1016/j.micpro.2020.103720.
- M. Giulietti and R. Vincenti, “Three-level secret sharing schemes from the twisted cubic,” Discrete Math., vol. 310, no. 22, pp. 3236–3240, 2010, doi: 10.1016/j.disc.2009.11.040.
- K. Meng, F. Miao, W. Huang, and Y. Xiong, “Tightly coupled multi-group threshold secret sharing based on Chinese Remainder Theorem,” Discret. Appl. Math., vol. 268, pp. 152–163, 2019, doi: 10.1016/j.dam.2019.05.011.
- J. Dhiman, “Implementation Algorithm of Improved Cryptography,” no. April, pp. 45–53, 2022, doi: 10.5815/ijitcs.2022.02.04.
- O. S. Adebayo, “Data Privacy System Using Steganography and Cryptography,” no. June, pp. 37–45, 2022, doi: 10.5815/ijmsc.2022.02.04.
- A. K. Biswas and M. Dasgupta, “ Two polynomials based ( t, n ) threshold secret sharing scheme with cheating detection ,” Cryptologia, vol. 44, no. 4, pp. 357–370, 2020, doi: 10.1080/01611194.2020.1717676.
- A. Mittal and R. Gupta, “An encryption method involving fourier transform and moore machine,” Int. J. Sci. Technol. Res., vol. 8, no. 11, pp. 3997–3998, 2019.


