Secure multiparty computation for privacy preserving range queries on medical records for star exchange topology

Published Online March 2018 in MECS DOI: 10.5815/ijcnis.2018.03.02

Many organizations keep registries that contain sensitive data on the same individuals. Very important analytics might be gained by these organizations, if the data in these registries could be combined and analyzed. For example, analyzing patients’ electronic medical records (EMRs) [1] shared among a set of hospitals. In such cases, new measures have to be used to ensure patient's sensitive data privacy [2].

Secure multiparty computation (SMC) protocols allow a group of parties to evaluate a common function or query securely, i.e., with the input of each party remaining private to all other parties. Researchers focused on protocols that support SMC while preserving data privacy or what is called 'privacy preserving SMC protocols'.

Those protocols either are based on “Real Model” where parties run and use their own SMC protocols without the need for trusted third party (TTP) or are “Ideal Model” where parties rely on a centralized TTP for computations [3].

In this paper, we present real model privacy preserving SMC to execute range queries on horizontally partitioned EMRs. The proposed technique adopts star exchange topology environment. The system relies on a head party as a mediator between the users and data owners without revealing the patients' privacy.

Our proposed technique is applicable for equality-test and range queries over horizontally partitioned data. It provides smaller computational costs depending on bucketization technique.

Experimental results showed that the proposed technique provides strong security and privacy by applying two types of encryption. We use a symmetric encryption scheme to encrypt patients' sensitive data and commutative encryption [4] to encrypt patients’ data more than once using different public keys and get the same result regardless the order of encryption.

In this paper, we present a detailed description of the proposed privacy preservation SMC techniques. The rest of the paper is organized as follows: Section II introduces the related work. Section III describes the proposed system. Experimental results are discussed in section IV and finally our paper is concluded and our future work is presented in Section V.

• II.    Related Works

This section reviews and discusses the main privacy preserving SMC protocols. These protocols enable query evaluation among multiple parties while preserving data privacy over distributed inputs, revealing only the query result. The research area in privacy preserving SMC can be based on either Garbled Circuits [5–11], SecretSharing [12-16], Oblivious Polynomial Evaluation [17– 20], Homomorphic encryption [21–27] or Commutative Encryption [4, 28–30].

Garbled circuit protocol [5–11] has first been developed by Andrew Yao for preserving data privacy by applying a symmetric encryption and an oblivious transfer protocol. However, Yao's protocol has a high communication complexity and requires the function and input sizes to be known in advance to allow precomputation [15], To be more specific; the oblivious transfer stage requires one exponentiation (e.g. public key encryption) per bit of input.

Secret-sharing protocol [12–16] allows the private data to be split into a set of encrypted shares and divide them between the participants. This protocol requires some random data to be encrypted in pre-processing phase to be combined with encrypted shares during computation. These shares are processed in privacy preserving protocol and then accumulated to get the output result. Goldreich-Micali-Wigderson (GMW) construction [12] uses a binary circuit representation of the function to develop secret-sharing protocol. The parties firstly secret-share their inputs using an XOR secret sharing scheme. To evaluate an XOR gate, the parties simply XOR the shares of the input wires. To evaluate an AND gate, the parties perform an oblivious transfer: one party pre-computes all possible outputs of the gate, the other party obliviously obtains the output that corresponds to its input shares. To obtain the output of the circuit, the parties exchange the shares of the output wires. The GMW protocol allows the pre-computation of all symmetric cryptographic operations before the function or the inputs to the function are known. It requires less communication per AND gate than Yao's garbled circuit protocol. However, the GMW protocol requires a number of communication rounds that are linear in the depth of the circuit [15].

Oblivious polynomial evaluation (OPE) protocol [17– 20] has been developed by Naor and Pinkas. The sender, who has a polynomial function F and the receiver who has an input x want to jointly compute F (x), so that the sender learns nothing about x and the receiver learns nothing except the output of F (x). To compare two items x and y by using OPE protocol, the receiver and the sender should each generate a random linear polynomial functions P and Q respectively to compute the two values so the receiver computes R = P (x) + Q (y) and the sender computes S = P (y) + Q (x). If R is equal to S then x = y; otherwise they are different with high probability. In case the receiver and the sender have a list of v inputs, the protocol requires each party to perform v oblivious evaluations of a polynomial of degree n with the communication cost of O (n). So, this protocol is considered too expensive to implement in the multiparty computation with large size data.

Homomorphic encryption allows computations to be executed on ciphertext and these computations will generate an encrypted result which matches the result of operations performed on the plaintext when decrypted. Homomorphic encryption is either partial or full homomorphic encryption. Partial homomorphic is used for computing specific-purpose functions [22–27]. Fully-homomorphic encryption (FHE) was proposed by Rivest et al. [21] to allow for a set of homomorphic operations, such as addition and multiplication. Homomorphic encryption requires computationally expensive publickey operations that scale very inefficiently for larger security parameters [15]. As mentioned in [31], while this technique offers strong privacy guarantee, it does not scale well for large-size data because of using heavy weight cryptographic operation among parties.

Commutative encryption protocol [4, 28 - 30] allows a plaintext to be encrypted more than once using different public keys where changing the order of keys has no effect on the query result. If there is a pair of encryption functions F and G to encrypt value v, the result of encryption will be F (G (v)) = G (F (v)). The conducted ciphertext can be decrypted by any participant without considering the order of public keys used in the encryption process. Thus, by using the combination F (G (v)) or G (F (v)) to encrypt v, we can ensure that one data owner cannot compute the encryption/decryption of value v without the help of the other data owner.

In this paper, the proposed work focuses on privacy preserving SMC protocols which support set-intersection and range queries.

Early SMC protocols only supported an environment setting that includes two-parties only [5, 12]. The relationship between SMC and privacy preserving SMC set-operations protocols came later, as a development of the idea of using MPC for computing set-operations in a privacy preserving manner [4, 32 - 34].

Freedman et al. [32] proposed a technique for setoperations queries using oblivious polynomial evaluation (OPE). In their protocol each party P i where i belongs to {1,…, m-1}, sends a polynomial F i to P m . The F i polynomial has degree s and is rooted in P i items. Then P m , for each item x in his list, sends s × (m - 1) matrix that is built in the point x of polynomials previously received from other parties. Receiving parties decrypt and combine the evaluations to determine whether their items belong to the intersection.

Sang et al. [33] adopted a distinct technique using OPE protocol, but provides lower computation and communication costs with respect to Freedman et al. approach [35].

Hazay and Lindell [25] proposed a different approach for securely computing the set-operations queries based on homomorphic encryption, but this approach still requires heavyweight encryption/decryption operations that are impractical for distributed settings [31].

Vaidya and Clifton [28] proposed a SMC technique for the set-operations queries based on commutative encryption as an extension to Agrawal et al. protocol. This technique has lower complexity than [32, 33].

Sepehri et al. [35] has proposed the time complexity comparison of solutions [4, 32, 33] for set-operations queries and found that the Agrawal et al. protocol has provided the least computation and communication cost.

Li et al. [36] proposed a protocol that involves a TTP to compare the values held by two other parties. The protocol is based on homomorphic encryption scheme. Although this protocol is faster than OPE as mentioned in [35], it has two main drawbacks: The TTP should be trusted by all parties. Additionally, the solution does not scale with the increase in parties because of the communication and computation bottleneck created at TTP.

Maryam et al. [31] proposed a privacy-preserving SMC technique for set-operations queries where the queries have to be executed on horizontally partitioned data. This data is held by different data owners who are arranged in the ring exchange topology environment. This technique relies on TTP only to begin the protocol execution.

Most of the aforementioned studies focused on privacy preserving SMC protocols for equality-test queries supporting environments where the ring exchange topology is supported. They involved the usage of a TTP to prevent data leakage in query computation.

In the remainder of this paper, we will focus on our proposed technique to preserve privacy of patients’ EMRs for equality-test queries and will extend the Agrawal’s original two-party equality-test queries protocol to support privacy preserving SMC for range queries over star exchange topology environment without the need for TTP. The proposed work is based on commutative encryption techniques to handle SMC for computing equality-test and range queries with smaller computational cost and better privacy.

• III.    Proposed System

In this section, we propose a real model of privacy preserving SMC technique to extend the Agrawal’s equality-test queries protocol to be applicable for privacy preserving SMC for equality-test and range queries.

In our solution, participants no longer need to trust or rely on a TTP; so we try to overcome this shortcoming by replacing the ring to star exchange topology. The topology supports a central/head node which acts as a mediator between all participants without revealing the sensitive data to provide end-to-end encryption (i.e. each node communicates with the head party). This mediator is not a TTP, it only acts as an interface between users and data owners. This topology can overcome the traditional shortcoming of the ring topology and provide more stability, scalability and better management to the multiparty environment.

The proposed system uses both symmetric and commutative encryption to provide a strong security and better privacy. In addition, we apply a bucketization technique to improve the efficiency of our technique by considering only records which are relative to the buckets containing the value searched by the user.

Our proposed system involves a set of hospitals as data owners, a common database of EMRs that have been horizontally partitioned among the hospitals and a set of authorized users 1 who are able to range queries the database for making analysis and knowledge extraction.

Our goal is to achieve both data and query privacy where the user knows only the query results while data owners learn nothing about the query.

• A.    Secure Multiparty Computation for Range Queries

In our solution, each patient has a medical record includes one searchable attribute T i,A that includes a set of values V A and at least one sensitive attribute T i,B that contains a group of values V B . Our technique applies bucketization technique on the searchable attribute to improve the efficiency of user range queries by reducing the search space.

Buckets are defined by dividing the domain of each searchable attribute A into S buckets of the size L as in (1).

^ A Max A Min

=      S                      ^(J

Public bucketization (BU) = {B 1 :[A min , L], ..., B S :(L (S-1) , A max ]}. It is accessible to all data owners and authorized users as well, where Amax and Amin are the maximum and minimum values in the domain of each searchable attribute A, respectively.

• B.    The Protocol

Our proposed protocol has two phases: Computation of permutation vectors and Query protocol.

Phase 1: Computation of permutation vectors

In this section, a step by step example is used to explain the computation of permutation vector. For simplicity used searchable attributes are integer values.

Input. Data owners O, number of buckets S.

Output. Owner permutation vector  Wi,  Head permutation vector H.

• ¹    Authentication and access control are not the main focus in this paper, we suppose that there are authorizations roles among the data owners and users.

Example:

We suppose that there are three hospitals as data owners O arranged in a star exchange topology environment where they all have one searchable attribute (e.g. Patient age) and one sensitive attribute (e.g. Patient disease). We assume that the domain of the patient’s age includes the values in the range [1, 100] and this domain is bucketized into S = 5 buckets, the size of these buckets L is the same and BU = {B 1 : [1, 20], B 2 : (20, 40], B 3 : (40, 60], B 4 : (60, 80], B 5 : (80, 100]}.

Step 1. Each data owner O i , 1 ≤ i ≤ M, selects its private permutation я / = (я / ,..., я / ) of bucket indices (1, 2,..., S) where S is the number of buckets and M is the number of data owners.

Step 2. Each data owner O i separately computes its private permutation ( B_n. ,..., B_n. ) for the searchable attribute of the BU schema.

Example (cont.):

Assuming that each data owner chooses his private permutation randomly from BU as the following:

Я1 = (3, 2, 1, 4,5)

я2 = (5, 2, 1, 3,4)

Яз = (3, 2, 1, 5,4)

For instance, n 1 shows that owner O₁ selects his own permutation as B 1 : (40, 60], B 2 : (20, 40], B 3 : [1, 20], B 4 : (60, 80] and B 5 : (80, 100] from BU boundaries and all the other data owners do the same.

Step 3. The head party chooses its own permutation H to send it to the data owners.

Example (cont.):

Suppose the head party chooses its own permutation H as the following:

H = (5, 3, 1, 4, 2)

Step 4. Each data owner O i computes his vector W where the vector elements are defined in (2).

In the following equation, we denote by H^-1(j) the position in vector H^-1 that contains value j.

W (j) = π δ  ∀ j ∈ {1,2,...,S},

δ = H ^{- 1}(J)                      ⁽⁾

Step 5. The head party sends its permutation H to the user who is initiating the query.

Example (cont.):

Each data owner computes his permutation vector W by (2) which is defined in phase 1 of the protocol.

The rationale behind (2) is generating the vector W for each data owner by determining the corresponding elements of private vector я. The vector W1 of the first data owner is obtained by searching for the index j position in the head party H permutation of his own private permutation я 1. For example, to get the vector elements W1 where j = 1 for the first element, head party looks in its H vector to get position which contains the value j = 1 and obtains 5 = 3. Hence, W1(1) = я5 = я3 = 1, which refers to the 3rd element in the vector я1. To make (2) more clear, we show how to get the second element in W1 where j = 2 for the second element, head party looks in its H vector to get position which contains the value j = 2 and obtains 5 = 5. Hence, W1(2) = я5 = я5 = 5, which refers to the 5th element in the vector я1.

So each data owner computes his W permutation vector and the head party sends its permutation to the user.

И = (1, 5, 2, 4,3)

И = (1, 4, 2, 3,5)

Из = (1, 4, 2, 5,3)

H = (5, 3, 1, 4, 2)^ u

Phase 2: Query protocol

Input. Query range r = (r min , r max ); user query values V R = {x ∈ N | r min ≤ x ≤ r max }

Set of buckets S with values A, VB> for each data owner, where VA is the searchable attribute and VB is the sensitive attribute.

Output. Set of tuples R = {t ∈ T | V A ∈ V R }

Example (cont.):

We consider that user query for the patients whose ages belonging to the range r = [38, 43]. According to the user range query, the proposed protocol applies an equality-test queries for each age value in this range:

V R = {38, 39, 40, 41, 42, 43}

Step 6. Both user and data owners O apply hash function h to their values, V R ' = h(V R ) and T' i,A = h(V i,A ) V i e {1, ..., M}, respectively, where M is the number of data owners, V R ' is the user hashed value and T' i,A is the searchable attribute hashed value for each data owner.

Step 7. User and data owners randomly choose commutative encryption keys, k_r and i, k'_i>, respectively.

Step 8. User encrypts his hashed value V R ' and then sends his encrypted hash value Y R = f k (V R ') to the head party.

Step 9. Each one of the data owners O i , 1 ≤ i ≤ M, performs the following:

• a.    Computes /_{k i} (T' i,A ) = Y i = {y i = f k_t (x)|x e V\,a }

• b.    Generates new symmetric keys, one for each value of sensitive attribute B, as K^B={ к/_х = f_k,.(x)|x e V i, A' }

• c.    Encrypts each value x in T i,B with the corresponding key k_ix to obtain Y iB = {E _k. (u)|u e V i, _B}, where E is a symmetric encryption function.

• d.    Computes I i = {(v, / к,. (v)) | v e Y R } for the purpose of decrypting the values of sensitive attribute B at the user site.

• e.    O i randomly reorders the tuples Y i and Y iB

Step 10. Step 10. The user determines his buckets B = {i | 1 < i < S} from the BU and sends BH_K to the head party to span it to all data owners, where k is the indices of the buckets which contain the values of user query.

Example (cont.):

The user determines his buckets’ numbers from the BU and sends them to the head party to span them to all data owners and then the data owners get their bucket IDs that correspond to user value, as shown in Fig. 1.

Step 11. At this step, each data owner O i selects his buckets which correspond to B_Hk of head party.

Step 12. Each data owner sends i, YiB , Ii> after randomly reordering to the head party in the star exchange topology environment.

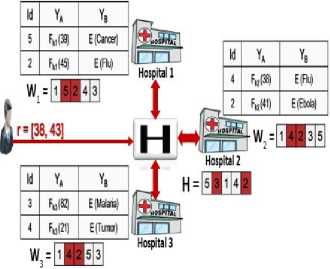
Fig.1. Data Owners Get Their Bucket IDs

Example (cont.):

Each data owner selects his buckets based on the searching range values of the user, as shown in Fig. 2.

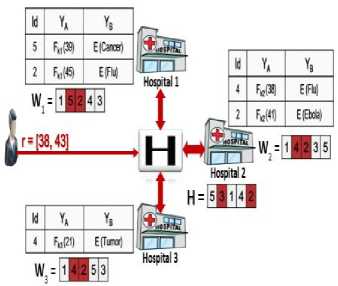
Fig.2. Each Data Owner Selects His Bucket

Step 13. Head party receives all tuples and then initiates Agrawal’s two-party set-intersection protocol between the user and the head party.

Example (cont.):

Head party collects all owners, as shown in Fig. 3.

encrypted tuples from data

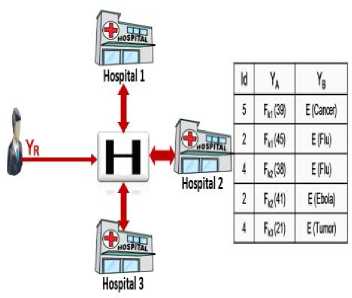
Fig.3. Head Party Collects the Encrypted Tuples

Step 14. Head party passes  YR  through the star exchange topology environment to encrypt its values by all encryption keys k1,…, km for obtaining Y'R = /к.(fkr(VR')), and after that, the head party sends Y'R together with to the user who initiated the query, for each i where 1 ≤ i ≤ M.

Example (cont.):

Head party passes Y R through the star exchange topology environment in order to have it encrypted with all keys of owners and get Y’ R , as shown in Fig. 4.

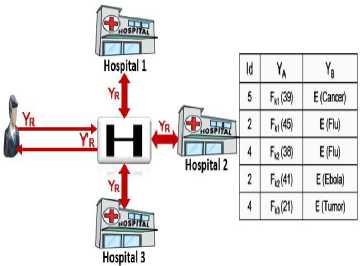
Fig.4. Encrypt user Value by All Keys of Owners

Step 15. The user then decrypts Y'R  using his commutative key kr to get Y"R = fkl(V^A).

Step 16. For each i where 1 ≤ i ≤ M, the user performs the following:

• a.    Finds all the tuples in Y i which are equal to the values of Y"_R . .

• b.    Determines the sensitive attributes which correspond to those tuples.

• c.    Decrypts I i with his own commutative key k r , to obtain fk₄(VVy

• d.    Uses f_k , (V' i,A ) to decrypt the sensitive attributes in Y B that correspond to Y i which their values are equal to query value of the user.

Example (cont.):

User decrypts Y’ R with his commutative decryption key to get Y” R and gets all the tuples in where the value of the encrypted searchable attribute is equal to Y” R as mentioned in step 15 & 16 of query protocol, as shown in Fig. 5.

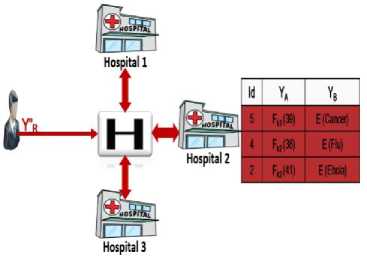
Fig.5. User Finds the Diseases That Correspond To Query Values

• C.    Correctness

We show that our protocol computes the query results correctly by proofing that each data owner chooses the correct buckets that include the query range values at each time (Show step 11).

• a.    General scheme

Each data owner O computes privately his W vector based on head party H permutation. The user searches for range values which falls in buckets ‘x’ of BU where 1 ≤ i ≤ S.

The head party sends H x to all data owners. Then, owners receive H x and compute b = {W(H x ) | 1 ≤ x ≤ S} to select buckets' numbers, then select his tuples Y(b) of the selected buckets.

• b.    Proof of correctness

Each data owner who has the data Y, computes b = {W(H x ) | 1 ≤ x ≤ S} and then selects his tuples Y(b).

Observe that by definition b = {W(H x ) | 1 ≤ x ≤ S} = Я д , where 6 = H^-1(H_X). Hence, b = n x , which indicates that the correct bucket is chosen by data owners.

• D.    Privacy Analysis

The protocol shows that the data owners choose the bucket IDs according to the query range values of the user. We have:

• a.    Indistinguishability of data distribution

Data owners privately choose their buckets which correspond to the query range values of the user. So the distribution of values that are hashed and also encrypted using commutative encryption is indistinguishable than uniform distribution.

• b.    Elimination of bucket inference

Data owners compute their W permutation vectors privately based on the head party H permutation vector which is known for both the users and each data owner. Data owners learn nothing about the permutation vector of the other data owners. Each data owner communicates only with head party and head party learns nothing about the buckets that are corresponding to the query value of user.

• IV.    Experimental Cost Analysis

In this section, we implemented some experiments to illustrate the benefit of using star exchange topology instead of the ring exchange topology and the importance of applying a bucketization technique for processing equality-test and range queries in SMC paradigm in terms of computation time.

We developed our technique using .Net languages on a Windows 8 platform with core i3 processor and 4GB RAM. In the experiments, we constructed 5 nodes, including three nodes for the three data owners (hospitals), one node for the head party and one node for the authorized user. Each data owner holds a table with one searchable attribute and one sensitive attribute for equality-test and range queries. We implemented a commutative encryption protocol based on exponentiation modulo p to encrypt the searchable attribute of each data owner’s table, and applied a symmetric encryption protocol (Advanced Encryption Standard) to encrypt the sensitive attribute.

We measured the computation time of our protocol for five different numbers of records which are partitioned horizontally among 3 hospitals as follows: N 1 = 1000, N 2 = 2000, N 3 = 3000, N 4 = 4000 and N 5 = 5000 records.

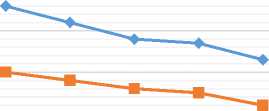
The experimental results, which are shown in Table 1 and Fig. 6, illustrate the difference in computational time for equality-test query for both the ring and star exchange topologies where the user query value is chosen randomly.

We extended the experiments of equality-test queries to be applicable for range queries, as shown in Table 2 and Fig. 7. We notice that the difference in computation time between the ring and star topology lines is fairly the same when the number of records is relatively small, but it differs as the number of records increases as shown in the graph lines. The results confirm the fact that the star exchange topology is effective in reducing the computation time when the number of records increases rather than the ring exchange topology.

Moreover, the star exchange topology provides better privacy since it does not need to rely on TTP where each data owner can separately compute its local permutations using the BU of head party without the need for building an interchange matrix between them. We deduced that our system is applicable for both the equality-test and range queries.

Table 1. Computational Costs of Our Protocol for Equality-Test Queries for Both Rang and Star Exchange Topologies with M = 3 Data Owners, S = 5 Buckets and V_r =55 Patient Age.

Number of Records (N)	Computational Time (Sec.) – Equality-Test Queries – Star Exchange Topology	Computational Time (Sec.) – Equality-Test Queries – Ring Exchange Topology
N 1 = 1000	0.8	0.9
N 2 =2000	1.5	1.7
N 3 = 3000	2.1	2.6
N 4 = 4000	2.6	3.4
N 5 = 5000	3.2	4.3

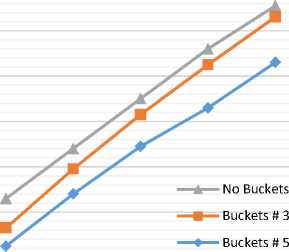
We tested the impact of increment the number of buckets on computational costs for equality-test queries of our protocol with the number of records N = 5000 and changed the number of buckets from 1 to 5 for both the star and ring exchange topologies, as shown in Table 3 and Fig. 8. We also analyzed the impact of increment the number of buckets on computational costs for range queries of our protocol with the number of records N = {1000, 2000, 3000, 4000 and 5000 records} and changed the number of buckets to be 1, 3 and 5 for star exchange topology as shown in Table 4 and Fig. 9.

4 3 2 о 1 о      0
	N1	N2	N3	N4	N5
Ring Topology	0.9	1.7	2.6	3.4	4.3
Star Topology	0.8	1.5	2.1	2.6	3.2

Table 3. Impact of Increment the Buckets Number on Computational Costs of Equality-Test Queries for Ring and Star Exchange Topology (N= 5000 records, M = 3 and 1 ≤ S ≤ 5).

Number of Buckets (S)	Computational Time (Sec.) - Ring Exchange Topology	Computational Time (Sec.) - Star Exchange Topology
1	5.6	4
2	5.2	3.8
3	4.8	3.6
4	4.7	3.5
5	4.3	3.2

Fig.6. Computation Time for Ring and Star Exchange Topologies (M = 3, S = 5 & V R =55).

Table 2. Computational Costs of Our Protocol for Range Queries for Both Rang and Star Exchange Topologies with M = 3 Data Owners, S = 5 Buckets and R = [38, 43] Patients’ Age.

Number of Records (N)	Computational Time (Sec.) – Range Queries – Star Exchange Topology	Computational Time (Sec.) – Range Queries – Ring Exchange Topology
N 1 = 1000	2.5	2.8
N 2 = 2000	4.8	5.5
N 3 = 3000	6.9	8.4
N 4 = 4000	8.6	11
N 5 = 5000	10.6	13.4

— ■ — Star Topology

Ring Topology

0	1	2	3	4	5
Star Topology	4	3.8	3.6	3.5	3.2
Ring Topology	5.6	5.2	4.8	4.7	4.3

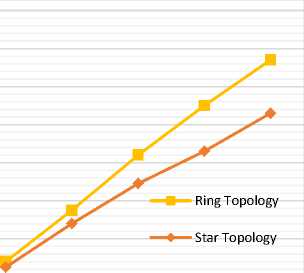
Fig.8. Impact of increment the buckets number on computational costs of equality-test queries for the ring and star exchange topologies (N = 5000 rows, M = 3, 1 ≤ S ≤ 5).

Table 4. Impact of Increment the Buckets Number for Star Exchange Topology (M = 3 and R = [38, 43]).

Number of Records (N)	Computational Time (Sec.) - Buckets = 5	Computational Time (Sec.) - Buckets = 3	Computational Time (Sec.) - No Buckets
N 1 =1000	2.5	3.3	4.6
N 2 =2000	4.8	5.9	6.9
N 3 =3000	6.9	8.3	9
N 4 =4000	8.6	10.5	11.2
N 5 =5000	10.6	12.6	13.1

0	N1	N2	N3	N4	N5
Ring Topology	2.8	5.5	8.4	11	13.4
Star Topology	2.5	4.8	6.9	8.6	10.6

0	N1	N2	N3	N4	N5
No Buckets	4.6	6.8	9	11.2	13.1
Buckets # 3	3.3	5.9	8.3	10.5	12.6
Buckets # 5	2.5	4.8	6.9	8.6	10.6

Fig.9. Impact of Increment the Buckets Number on Computational Costs for Range Queries (M = 3, S = {1, 3, 5}).

We noticed that, when the number of buckets changed in an increasing order, the computation time changed in a decreasing order. We deduced that the bucketization technique improves the efficiency of our protocol by considering only records relative to the buckets containing the value searched by the user. In this way, the data owners work only on a subset of their data at each round, leading to a more scalable protocol.

• V.    Conclusions

In this paper, we proposed a technique for both equality-test and range queries. In our solution, participants no longer need to rely on a TTP; as we overcame this shortcoming by migrating from ring to star exchange topology between participants where there is a central/head node which acts as a mediator between all participants without revealing the sensitive data. Our technique is based on the commutative encryption protocol, which provides strong security and better privacy. In addition, we have applied bucketization technique to improve the efficiency of our technique by considering only records which are relative to the values of user range query. Data owners do not learn the query and the head party learns neither query nor query result. In our future work, we will try to adopt our technique to support inner-join queries.