Secure video compression and integration technique for data transmission

Published Online November 2017 in MECS

Digital video [1] is a description of a real-world natural or a visual scene, which sampled temporally and spatially, whereas video coding is compression and decompression process. Image or video transmission requires compression to decrease the quantity of data for fast and secure transmission and encryption [2][3] is used to protect the use of data against unauthorized access.

In general, videos require a huge volume of data. Data transfer using wireless and processing systems i.e power, memory, and is hardly able to handle the heavy encryption process. To handle complex data and to secure, new video encryption algorithms need to be developed. A video encryption algorithm must be good in terms of various parameters such as efficiency of compression ratio and computational, security. Security levels differ for the different video. Defense or Banking information requires the high level of security to prevent unauthorized access, whereas for online video requires low security.

In communication network, data exchange presents certain risks factor, which requires the existence of appropriate security measures. For example, the images are transmitted and can be copied or saved during their transmission without loss of image quality. During an exchange images can be hacked in time of digital information storage and reproduce illegally. It is therefore necessary to develop software for effective protection of transferred data against arbitrary interference. Data encryption with image merging is very often the only effective way to meet these requirements.

Digital information loss and its recovery is still one of the biggest concern in digital communication networks. Interleaving schemes is important mechanism in reducing the effect of network error on image transmission. Interleaving schemes spatially de-correlate neighboring image blocks by putting them into packets that are far distant apart from each other in the transmission sequence. Most of the existing schemes do not offer the same performance in the case of bursty packet losses as it does on random packet losses.

Advanced digital technologies and growth of computer networks, a huge amount of digital data is being transferred over various types of networks. A large part digital data of this information is either private or confidential. Most of the security algorithms specifically designed to encrypt digital data are proposed in the mid-1990s. Encrypt and decrypt of images can be done by different encryption algorithms. There are two groups of cryptography image encryption algorithms: (a) Non-chaos selective methods and (b) Chaos-based [4] selective or non-selective methods. It can be admitting, no particular encryption algorithm which satisfies all image type requirements. An Encryption Algorithm should be strong against all types of attacks, including statistical and brute force attacks. Different security algorithms have been used to provide the required protection and many encryption algorithms have been proposed to enhance the image security.

The process of image encryption [1], [2] is to convert an image to another format that is hard to understand. The reverse process is on other hand that retrieves original image is by decryption. The transformation of information in secure manner is based on encryption. Video compression proposed here is to reduce the size of the data and to reduce the bandwidth so that the encryption will be strong against all types of attacks. Here we present, compression and encryption as the first stage and then process by image interleaving along with pixel integration method to enhance security.

In order to increase the image entropy value and to decrease the high correlation among pixels, and thus an improved security level of the encrypted images, we propose a process based on interleaving the columns and rows of the image using the pixel based technique for image merging. The interleaving process will be used to split (divide) the original image into a number of blocks that are then shifted through the columns and the rows within the image before the encryption process starts. The generated image is then processed into the ECC encryption algorithm.

In proposed approach, a set of nine sample videos are taken as input and 3 frames per video are extracted for integration. These frames are converted as RGB with n*n pixel size are considered. These pixel values with block the size of 4*4 is considered for testing, to evaluate the design parameters. First compressing with H.264 standard [5] and encrypting with Elliptical Curve Cryptography (ECC) [3], [6] then Interleaving with Pixel based Integration to generate multi video, decryption is done based on the selection of the key in reverse order. The compression ratio of each layer, entropy and correlation are calculated and evaluated.

• II.    Related Work

In the first group, Liu et al. [7] approached encryption algorithm for image based on an iterative random phase encoding. Mapping is done based on two-dimensional chaotic, to create random data for iterative random stage encoding. In [8], an encryption algorithm for the color image using an Arnold transform and discrete fractional random transform in the intensity-hue-saturation (IHS) color space has been suggested. Each color space component is then encrypted separately by different approaches. In, Arnold transforms and the gyrator transform based image encryption algorithm is proposed. In [9], multi-image integration is proposed which is based on block-based interleaving, with pixel based integration technique and Encryption with Advance Encryption Algorithm. Performance is evaluated by calculating the co-relation coefficient and information entropy.

In the second group, Abd Samad Bin Hasan Basari et al. [10] approached a new encryption algorithm for images by rotation, where images are divided into 6 sub-images and these sub-images are further divided into small blocks as shown in Fig.1 and 2. These small blocks are then attached to the faces of magic cubes. Correlation and Entropy values are shown in Table.1. In [11] approached compression and encryption method simultaneous which based on optically set. The major strength of the method is in its robustness against various known-plain text attacks making this algorithm appealing for color video images and the main drawback it can use only for optical setup images, not for other images.

In the third group, Daniel Schonberg et al. [12] proposed framework on compression of encrypted images and video sequences. In [13] proposed algorithm for image encryption using ECC based on pixel grouping. The group of pixels will reduce the computation and are transformed into a big integer. These big integer values are paired and given as input in ECC operation. In [14] proposed encrypting the image based on pixels by applying ECC. First, scrambling the image pixels, through the method of the watermark. Getting final encryption image is by camouflaged image to vision.

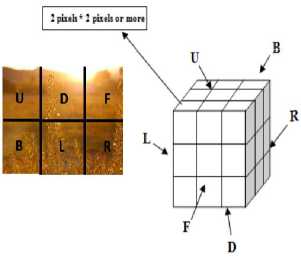
Fig.1. Magic Cubes Six Sub-images

Fig.2. (a) Image Input. (b) Encrypted image using AES (c) Rotation image. (d) Encrypted Image using Intergration Technique.

In fourth group Zhi-Hong Guan et al. [15] proposed a new image encryption scheme, in which shuffling the positions and changing the grey values of image pixels are combined to confuse the relationship between the cipherimage and the plain-image. The discrete output signal of the Chen's chaotic system is preprocessed to be suitable for the grayscale image encryption, and the shuffled image is encrypted by the preprocessed signal pixel by pixel. Rogelio Hasimoto Beltran et al. [16] proposes interleaving scheme where the de-correlation process is applied not only at a block, but also at a pixel or coefficient level in the compressed domain. The de-correlation is achieved via a k-way shuffle of pixels among the blocks and using the spatial properties of different space filling curves, k depends on the total number of blocks in the image.

Table 1. Correlation of Two Pixels and Entropy value for image divide into 3*3 pixels

Image	Correlation Analysis				Entropy Value
	Horizontal	Vertical	Diagona l	Anti-Diagon al
A	0.9951	0.99355	0.9917	0.9914	7.0443
B	-0.0444	-0.0476	-0.0208	-0.0317	7.9256
C	0.5220	0.5887	0.3820	0.3898	7.1766
D	-0.0449	-0.0520	-0.0433	-0.0388	7.9448

• III.   Proposed Work

• A.    H.264 Compression

H.264 defines a method of coding video that can give better performance than any of the preceding standards. It compresses video into a smaller space, which means that a compressed video clip takes up less storage space compared to older codecs and less transmission bandwidth. Generally, standard definition is available in the DVD-video format, capable of supporting only a single movie where as High definition videos with H.264 compression, to record hours of video on a memory card and to deliver video streaming over in online. First, the given input videos are converted into frames in RGB format.JPEG compression is applied to all image layers individually for better performance. H.264 video compression technique consists of 4 functional stages.

• 1.    Converting the video into frames.

• 2.    RGB image format.

• 3.    Using     discrete     cosine     transform(DCT)

• 4.    Quantization of the blocked frequency domain data per a user-defined quality factor

transformation of a blocked representation of RGB data to frequency domain representation

• B.    Elliptic Curve Cryptography

Elliptical curve cryptography (ECC) [3] function is based on public key encryption technique based on elliptic curve theory that can be used to create efficient cryptographic keys which is smaller and faster. Key generated through the properties of the elliptic curve equation instead of the traditional method of generation as the product of very large prime numbers.

• C.    Image Encryption

The encryption procedure is based on encrypting the image intensity and thus converting it into a new intensity. This new intensity is decrypted to obtain the original intensity.

• 1.    Read the image and find the intensity I from the image intensity matrix.

• 2.    Convert the intensity of the image I into an elliptic curve point E using Mapping-1.

• 3.    Elliptic curve point from Mapping-1 Encrypted to a

• 4.    The new point (E') is converted to a corresponding integer M, using Mapping-2.

• 5.    This integer M is used to calculate the new encrypted intensity I.

new point(E').

• D.    Image Decryption

• 1.    The decryption is done by reverse process of encryption.

• 2.    The encrypted image intensity I’ is read from the received files.

• 3.    The intensity I parameter is to calculate the integer M.

• 4.    Integer M is converted to encrypted elliptic curve point E’, using reverse mapping-2.

• 5.    The encrypted elliptic curve point E’ is decrypted to get the original point E.

• 6.    By reverse mapping-1, the original intensity I is obtained.

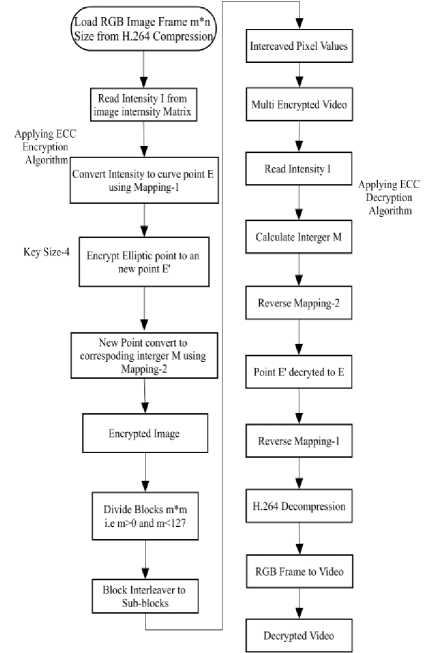
Fig.3. ECC Algorithm

• E.    Image Interleaving

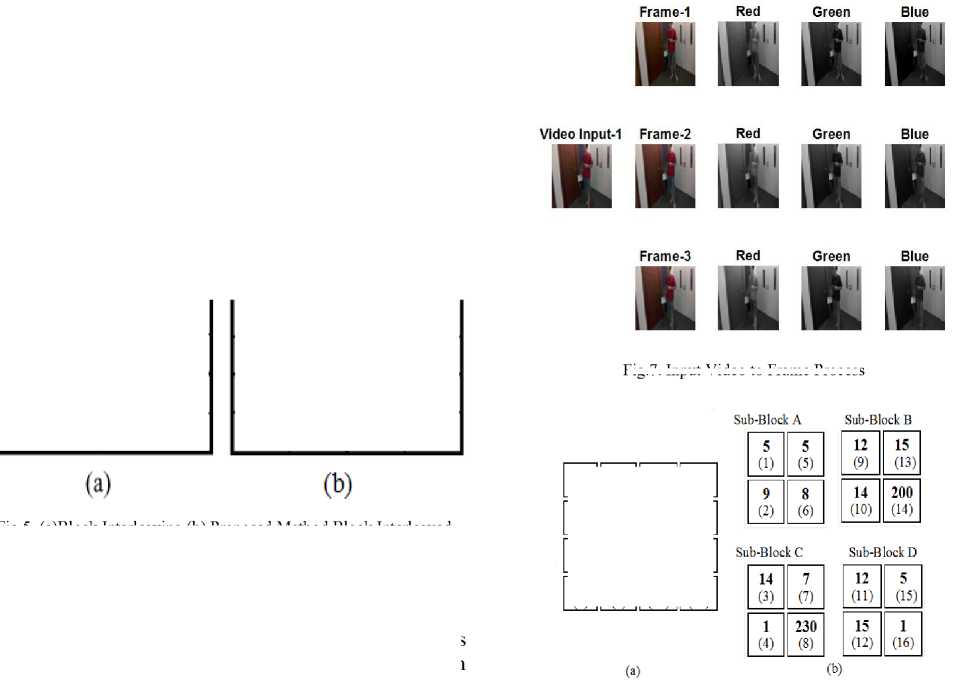
Encrypted RGB frames are divided small blocks [17] [18] as 4*4, for better security the block size should be small. These sub-block images are interleaved column wise. The number of sub-block pixel values in each block is fixed for a given interleaver. The interleaver operation on a set of image pixel values is independent of its operation on all other sets of symbols Applying block based interleaving by selecting the initial location randomly.

In 2D type of interleaves, the idea of extending from 1D prime interleaved into two dimensional is utilized. The concept of proposed 2D prime block based interleaved is follows: Consider the two-dimensional interleaving of nr by nc matrix. Firstly, we divide the interleaving scheme into column-wise interleaving and row-wise interleaving. Secondly, we assign the value of seed as column-wise seed and row-wise seed to columnwise interleaver and row-wise respectively. Therefore, the location of bits after interleaving will be as follows.

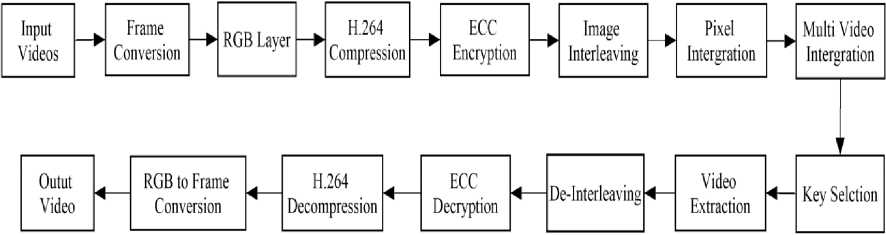
Fig.4. Block Diagram of Proposed System

Row-wise

1-1

2-(l+ptD-1-) mod nr ЗЦЛ+Зрк™) mod iir nr-(l—(Hr-1) Prow)

Column-wise

1-1

2-(l+p™i) mod lie

3-(l+2pCci) mod lie

ПС-(1+(Пс-1) p™l)

where p row and p col are row-wise and column-wise seeds. After we get the new location of bits after interleaving on both row-wise and column-wise, the new locations are mapped back into 2D interleaver to get the resulted interleaved bits in 2D.

F. Color Format

Fig.5. (a)Block Interleaving (b) Proposed Method Block Interleaved Sequence

Al	A2	Bl	B2
A3	A4	B3	B4
Cl	C2	DI	D2
C3	C4	D3	D4

Al	Cl	A2	C2
DI	Bl	D2	B2
A3	C3	A4	C4
D3	B3	D4	B4

16-bit Color: Each pixel is represented [1] using 2 bytes or 16 bits. The bits are divided as red, blue and green each having values i.e. 5-bits for red, 6-bits for green, and 5-bits for blue.

True Color (24 bit): each pixel color is represented using 3 bytes, one for R, one for G, and one for B.

True Color (32bit): An extra byte is used and rest same as 24-bit true color, usually referred to as the alpha component, used to specify transparency.

Fig.7. Input Video to Frame Process

5 (1)	5 (5)	12 (9)	15 (13)
9 (2)	8 (6)	14 (10)	200 (14)
14 (3)	7 (7)	12 (11)	5 (15)
11 (4)	230 (8)	15 (12)	(16)

Fig.8. (a) Input Frame Pixel value for 4*4 Size (b)Sub-blocks Value for (a)

G. Pixel Integration Technique

Consider image input RGB frame of size m*m,

Red=5bits Green=6bits              Blue=5 bits

Fig.6. 16-bit color Format

Step 1: The input images frame RGB are represented as pixel values ranging from 0-255.

Step 2: Create a pixel integration table column and row wise, forming pixel values in the columns with values 1-266 and the input images are taken along the rows.

Step 3: Choosing the sub-blocks as 4x4 as shown in figure.8 and 7 by dividing the image matrix, since we consider the color depth of image as 16-bit.

Step 4: Considering an RGB frame size of 64x64 and dividing into 4x4 blocks will produce 16 blocks i.e Sub-Block A, B, C and D.

Step 5: Considering the first sub-block A(i,j),where i represent pixel value and j represent index(location). The pixel integration table is created as shown in fig.9 by assigning the pixel index to the corresponding pixel value for the first block of RGB frame of every image, later the second block of every image, and so on till the last block.

Step 6: In case of multiple indices with the same pixel value in a block, the value is calculated by representing them in the 16-bit color RGB palette as shown in figure.9 and finding their corresponding value as shown in fig.10.

Step 7: This process is carried on for all the blocks of the image and the results are noted.

Step 8: Image Integration is finally done by summing up the pixel indices value for each pixel value for all the images taken together

Im age, Tixel	1	2	3..	10
1	4,16
2	9
3
4
5	1,5,15
6
7	7
8	6
9	2
10
11
12	9,11
13
14	10,3
15	13,12
200	14
230	8
256

Fig.9. Pixel Integration Table with Values

Fig.10. Multiple values Location in RGB Format

• IV.    Experimental Details And Results

The proposed method has been implemented in MatLab 8.6 in windows environment with a system configuration of I7 Intel Pentium VI Generation processor with 16 GB RAM. The proposed algorithm has been tested with various images. A good quality encryption algorithm should be strong against all types of attack. Another important factor that evaluates the efficiency of algorithms is measuring the amount of time required for overall process. Some experiments are given in this section to demonstrate the efficiency of the proposed technique.

• A.    Correlation Co-Efficient

The correlation [19] is analysed between input image and encrypted image, which is called the correlation coefficient, ranges from -1 to +1. If the encrypted image correlation value is equal to zero or very near to zero, then the encrypted image and original image are totally different, i.e., the original image has no features and is highly independent from the encrypted image. The encrypted image is a negative of the original image, if the correlation is equal to -1. Correlation coefficients were calculated by using the following equation (1), (2) and (3),

Cov(x,y)

'^ = VD(x)VD(y)

E(x) = 1 X^xt, D(x) = 1 1 ?=1 (х_г - E(x))  (2)

Where x, y is input image and encrypted image values of two adjacent pixels in the image. In numerical computation, the following formulas were used.

Cov ^(x, y) = ¹ Z ”=i ^(x t ^{- E(x}))⁽ y t ^{- D(x))} (3)

The obtained correlation coefficient for encrypted counterpart is shown in Table II, III and IV.

• B.    Information Entropy

Information entropy [20] is defined to express the degree of uncertainties in the system. A secure encryption should provide a situation which the encrypted image is not provided any information about the original image. On the other hand, higher entropy images such as an image of heavily cratered on the moon have a great deal of contrast from one pixel to the next and consequently pixel cannot be compressed as much as low entropy images. Entropy indicated that each symbol has an equal probability. The information entropy for encrypted is calculated using equation no (4),

H = -Ы x log₂P_t        (4)

Where,

H=Entropy of image

N=Gray level of an input image (0-255)

Pi=Probability of the occurrence of symbol i

• C.    Compression Ratio

  

  Fig.11. Input Videos with Frame-1

  
  

Compression ratio is the process of reducing the size of a data file. In the transmission of data, it is called source coding in opposition to channel coding. Compression is useful because it reduces resources required to transmit and store the data. Compression ratio is called with the below formula, uncompressed, size Compression ratio = ------------—:--- compressed size

Thus, a representation that compresses a 10 MB file to 2 MB has a compression ratio of 10/2 = 5, often notated as an explicit ratio, 5:1 (read "five" to "one"), or as an implicit ratio, 5/1. Note that this formulation applies equally for compression, where the uncompressed size is that of the original; and for decompression, where the uncompressed size is that of the reproduction.

Fig.12. Input Videos with Frame-2

Sometimes the space savings is given instead, which is defined as the reduction in size relative to the uncompressed size as:

compressed size

Space Savings = 1 - ----------—— uncompressed size

Thus, a representation that compresses a 10MB file to 2MB would yield a space savings of 1 - 2/10 = 0.8, often notated as a percentage, 80%.

Fig.13. Input Videos with Frame-3

For signals of indefinite size, such as streaming audio and video, the compression ratio is defined in terms of uncompressed and compressed data rates instead of data sizes as:

Uncompressed Data Rate

Compression ratio = —---------, _ .  „ .—

Compressed Data Rate and instead of space savings, one speaks of data-rate savings, which is defined as the data-rate reduction relative to the uncompressed data rate as:

Fig.14. Encrypted Video

Compressed Data Rate Data Savings Rate = 1 - -------------, _ .  „ .

Uncompressed Data Rate

When the uncompressed data rate is known, the compression ratio can be inferred from the compressed data rate.

• D.    Result Analysis

  

  Fig.15. Decrypted Video, Key No.4

  
  

  High compression ratio with high information entropy values achieves good encryption along with low correlation values. The simulation time period for video encryption and video decryption with the specific key is 197.1251 sec.

Fig.16. Decrypted Video, Key No.7

Results for the compression ratio for each frame image for RGB layer, correlation co-efficient value and the entropy values are shown in Tables II, III and IV. The correlation values are very low and negative values which produces high encryption standard corresponds to high entropy value and compression ratio.

Table 2. Compression Ratio, ENTROPY and CORRELATION Value for Input Video-Frame-1

Image No	Compression Ratio			Entropy Value	Correlation Value
	R	G	B
1	0.5469	0.5625	0.5625	0.0537	-0.0130
2	0.6875	0.6719	0.7188	0.0009	-0.0065
3	0.3906	0.4063	0.3906	0.0001	0.0061
4	0.4844	0.5625	0.5313	0.0005	-0.0014
5	0.5781	0.5469	0.5469	0.0000	0.0346
6	0.5313	0.5313	0.5313	0.0253	-0.0240
7	0.3906	0.4844	0.5000	0.1739	-0.0050
8	0.5469	0.5781	0.5938	0.3185	-0.0071
9	0.5000	0.5625	0.5469	0.0158	0.0320

Table 3. Compression Ratio, ENTROPY and CORRELATION Value for Input Video-Frame-2

Image No	Compression Ratio			Entropy Value	Correlation Value
	R	G	B
1	0.5469	0.5625	0.5625	0.5459	-0.0129
2	0.6875	0.6719	0.7188	0.6875	-0.0065
3	0.3750	0.3750	0.3750	0.0001	0.0060
4	0.5000	0.5938	0.5313	0.0005	-0.0015
5	0.5781	0.5469	0.5469	0.0000	0.0343
6	0.5313	0.5313	0.5313	0.0252	-0.0238
7	0.3594	0.4688	0.5000	0.1739	-0.0050
8	0.5469	0.5781	0.5781	0.3186	-0.0071
9	0.4844	0.5469	0.5156	0.0158	0.0317

Table 4. Compression Ratio, ENTROPY and CORRELATION Value for Input Video-Frame-3

Image No	Compression Ratio			Entropy Value	Correlation Value
	R	G	B
1	0.5469	0.5625	0.5625	0.0537	-0.0128
2	0.6875	0.6563	0.7031	0.0010	-0.0065
3	0.3594	0.375o	0.3594	0.0001	0.0060
4	0.5156	0.5938	0.5313	0.0005	-0.0015
5	0.5625	0.5469	0.5625	0.0000	0.0341
6	0.5313	0.5313	0.5313	0.0252	-0.0237
7	0.3281	0.4844	0.5000	0.1739	-0.0049
8	0.5469	0.5781	0.5781	0.3186	-0.0071
9	0.4688	0.5625	0.5625	0.0158	0.0315

• V.    Conclusion

Due to data transmission of digital information using wireless and processing systems, security has become a primary concern. To increase the security and to avoid data hacking, compression and encryption with pixel integration method are approached in this paper. First, compressing the input video frame and encrypting along with the interleaving and then by pixel integration produce an integrated video which makes difficulty to decode. Test results have been carried out utilizing detailed numerical analysis which shows the strength of the proposed algorithm. The proposed algorithm presented exists a direct relationship between the number of blocks and entropy and inverse relationship between the number of blocks and correlation This technique is expected to show good performance with low correlation coefficient value, high information entropy, and high compression ratio. Moreover, test result shows performance evaluation of proposed image encryption algorithm is highly secure which makes to encrypt large sets of data simultaneously and efficiently. The proposed method will be used in transmission applications and real-time video encryption.