Secured Lossy Color Image Compression Using Permutation and Predictions

Published Online June 2017 in MECS DOI: 10.5815/ijigsp.2017.06.04

An immense amount of data is required in the field of image processing. The general problem of image compression is, to reduce the amount of data required to represent a digital image and the basis of the reduction process is the removal of spatial and psychovisual redundancies [3]. The compression can be either lossy or lossless. In lossless compression the reconstructed image is identical to the original image but in lossy compression method, it is not.

In the present scenario especially in the corporate world, through the internet, the images travel rapidly and widely, in multiple manifestations. Confidential data in image form needs to be distributed through various sectors without any leakages. Compression alone will not be sufficient as anyone can access the image; hence encryption is required to allow only authorized persons to access. Controlling and protecting sensitive or confidential images are the process of Image security [4].

Preprocessing the image and transforming it into some intermediate form can be compressed with better efficiency to avoid natural redundancy.

Government, military and private business organizations are having huge amount of confidential images [5]. Most of this information are stored in the computers and transmitted through internet to the other connected computers. When the confidential image is accessed by an unauthorized person will lead to lot of problems.

To transmit secret images to people connected thought internet number of encryption schemes are available. Those schemes are classified into the following three types namely Position Permutation, Value Transformation and Visual Transformation [6].

Encryption plays a vital role in securing the images from the attacks while at rest as well as in transit[7]. Image Compression and Encryption Schemes are classified into two types, Compression-then-encryption and encryption-then-compression. There are very less chance to access the image and the image size is more in the later method. Former has chance to access the image with reduced size.

This paper discusses categorization (rigid and elastic part separation) and evaluation of simultaneous image encryption with compression.

The rest of this paper is organized as follows: Section II discusses about the related work. Section III discusses about the proposed methodology. Section IV describes about the analysis of the research work based on the performance evaluation factors. Finally in Section V conclusion is discussed.

• II.    Related Work

  • S.S.    Maniccam and N.G. Bourbakis [8] have presented SCAN methodology which performed both lossless compression and encryption of 512×512 gray-scale images.

Masanori Ito et al. [9] proposed a method by combining encryption and compression based on Independent Component Analysis (ICA) and Discrete Cosine Transform (DCT). The target images are shielded with an insignificant image and their combinations to be transmitted are obtained by way of encryption. The original images are reconstructed by applying some Independent Component Analysis (ICA) algorithm to the combined images. The DCT and simple low pass filter are used in the compression. The quality of the reconstructed image is reduced, because the higher frequency components were cut off.

V.Radha and D.Maheswari [10] proposed an image encryption algorithm that consists of two parts: scrambling of plain-image and mixing operation of scrambled image using discrete states variables of chaotic maps. The Discrete Cosine transform is used for compression. It reconstructs the image with high security and great speed but its compression ratio is less.

Wei Liu et al. [11] used stream cipher based Slepian-Wolf coding for encryption with progressive lossless reconstruction.

D.Ranjani 1, G. Selvavinayagam [13] proposed a highly efficient image Encryption-Then-Compression system. Discrete Wavelet Transform is used for encryption and 2D Haar Wavelet Transform is used for compression.

Shih-Ching Ou et al [14] proposed a new compression method with encryption system for internet multimedia applications. Significance-Linked Connected Component Analysis (SLCCA) method is used for compression and AES is used for encryption.

B.C.Prudhvi Teja and M.Venkatesh Naik [15] proposed a new system that uses random permutation based encryption with Haar and Daubechies Wavelet Transform based compression.

• III.    Methodology

This paper proposes a new color image compression scheme for encrypted images. The compression process is shown in Fig. 1.

Initially the input image is encrypted using the pseudo random permutation process. Then the encrypted image is divided into rigid data and elastic data [1]. The rigid data is compressed in the visually lossless manner and the elastic data is subject to lossy compression.

Error_H = Original_H – Predicted_H (1)

Error_LH = Original_LH – Predicted_LH (2)

Then the Error-LH and Error-H information are quantized using the Equation 3.

EQ tj = fix^)             (3)

Ч с

Where E_t j is Error pixel data at i,j^th location

EQ tj is Quantized error data at ij th location q_c is Quantization Constant = 2

Before the quantization process, the information is distributed in the range 0 to 255. The error information occupies one byte (8 bit) data storage. After the quantization process the error information is distributed in the range 0 to 127. This quantized information occupies 7 bit data storage for each rigid pixel.

The sign information of the error data is extracted. The negative sign is indicated by 1 and the positive sign is indicated by 0. The LSB of the error information is modified by either 0 or 1 in order to embed the sign information. So there is no need of carrying the sign information using extra bits. It is known as negative sign removal process. This is performed using Equations 4 and 5.

EE_t j = fix (—) * 2 + Func_Sign(EQ_iJ)    (4)

Func_Sign(EQ_t j ) = {1 ^{if EQtj} <  ⁰ }      (5)

0 otherwise )

Where EE ^ j is 7 bit error pixel data after the sign is removed at i, j^th location

F'unc_Sign(EQ_i j ) is sign extraction function

These 7 bit rigid data are converted into 8 bit sequence i.e. 7 bit data are placed continuously in the linear form. Then the continuous 8 bits are grouped as a single byte data and these data are used to form the integrated linear error information.

Finally, LL and the integrated linear error information is combined to form a new rigid data. The Huffman compression is applied on the new rigid data.

The elastic data is compressed using Xinpeng Zhang [1] method to reduce 8 bit elastic information into 2 bit information. The compressed elastic data and the Huffman output are concatenated to construct the final compressed data.

In the decompression section the compressed rigid data and the compressed elastic data are separated. Inverse Huffman is applied on rigid data to get the original-LL and the error information.

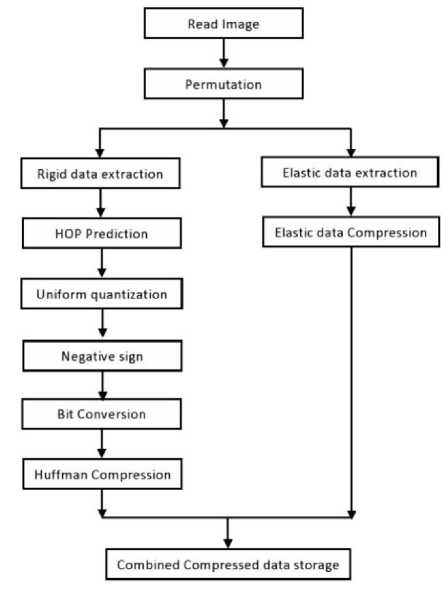
Fig.1. Proposed compression Scheme

The 8 bit error sequence is converted into 7 bit data sequence. The negative sign information is extracted from the LSB of the 7 bit data sequence using the Equation 6.

_Fn..t -1* ^EEi ^ , ^{if m0d} ( ^EEU , ²) = ¹ I

• ^1,1    (EE tj otherwise                      J

Where EQ ^j is 7 bit error pixel data after sign restoration at i, j^th location.

The extracted sign information is used to restore the 7 bit data sequence. The error information is subject to the inverse quantization process using Equation 7.

IQ tj = EQ^ * q_c                (7)

Where IQ t j is Error pixel data at i,j^th location

The predicted-LH is constructed using the original-LL using the HOP prediction. The reconstructed-LH is obtained by adding the predicted-LH and error-LH using Equation 8.

Reconstructed_LH = Predicted_LH + Error_LH (8)

The original-LL and the reconstructed-LH are used to generate the reconstructed-L using Equation 9.

Reconstructed_L = FI(Original_LL, Reconstructed_LH)              (9)

Where FI is a function for the integration

The HOP prediction is applied to generate the predicted-H using reconstructed-L. The predicted-H and the error-H are used to form the reconstructed-H using Equation 10.

Reconstructed_H = Predicted_H + Error_H    (10)

The reconstructed-L and the reconstructed-H are continued to reconstruct the final rigid data using the integration process given in Equation 11.

RigidData = FI( Reconstructed_LReconstructed_H) (11)

The RigidData is the final decompressed rigid data. Then the Xinpeng Zhang [1] method is used to decompress the elastic data with the help of rigid data. The elastic data decompression process involves a joint decompression with encryption to reconstruct the output image.

• IV.    Experimental Results

Various experiments are conducted to analyze the performance of existing methods such as encrypted JPEG-LS, encrypted HUFFMAN and Ximpeng Zhang method against the proposed method.

JPEG-LS [16] is one of the lossless coding of still images. The main objective of JPEG-LS is to yield a low complexity solution for lossless image coding with the better possible compression efficiency.     In the implementation, the input image is encrypted and it is compressed using JPEG-LS method. It is referred as the Encrypted JPEG method (EJPEG).

The Huffman coding is a variable-length coding algorithm which is used for lossless compression. It is a method for the construction of minimum-redundancy codes. A source symbol is encoded in a particular way based on the estimated probability of occurrence for each possible value of the source symbol.    In the implementation phase, the Huffman coding is applied after the image encryption. It is referred as Encrypted HUFFMAN method (EHUFFMAN).

The Xinpeng Zhang [1] method delivers a scheme for encrypted image compression in lossy manner. This methodology includes the components of joined image encryption with compression and joined decompression with decryption. In the decompression section an iterative approach is proceeded.

A good system provides maximum secrecy with maximum  fidelity using  the least number of bits/symbol[17]. The Time Consumption performance of the proposed system is tabulated in Table 1. From Table1, it can be inferred that the proposed work gives compression ratio around 1.5 for color images. The Fig 2 shows the experimenal compression ratio with various methods.

c                             d

f

e

g                           h

i                                                        j

• Fig.2.    Compression stage : a. Original color image b. Red channel color image c. Encrypted Red channel d. HOP Red channel e. Green channel color image f. Encrypted Green channel g. . HOP Green channel h. Blue channel color image i.

Encrypted Blue channel j. HOP Blue channel

a                               b

c                                d

e                                     f

g                           h

i                                                        j

• Fig.3.    Deompression stage : a. HOP Red channel b. Decrypted Red channel c. Enhanced Red channel d. HOP Green channel e. Decrypted Green channel f. Enhanced Green channel g. . HOP Green channel h. Decrypted Blue channel i. Enhanced Blue channel j. Reconstructed Image

Table 1. Performance analysis with CR for PSNR 34.60 db

Image Name	Algorithm	CR
Fruit.bmp	EJPEG	1.1085
	EHUFFMAN	1.1359
	Xinpeng Zhang	1.388
	Proposed	1.5238
Lena.bmp	EJPEG	1.1002
	EHUFFMAN	1.1346
	Xinpeng Zhang	1.388
	Proposed	1.5201

Table 2. Performance analysis with compression and decompression time consumption

Image Name	Algorithm	Time Taken
		CTT	DTT
Fruit.bmp	EJPEG	1.0608	0.7176
	EHUFFMAN	1.3414	0.4668
	Xinpeng Zhang	3.7908	3.588
	Proposed	6.2858	8.3995
Lena.bmp	EJPEG	0.8736	0.4056
	EHUFFMAN	1.1544	0.5772
	Xinpeng Zhang	2.5428	2.6988
	Proposed	6.9589	7.8825

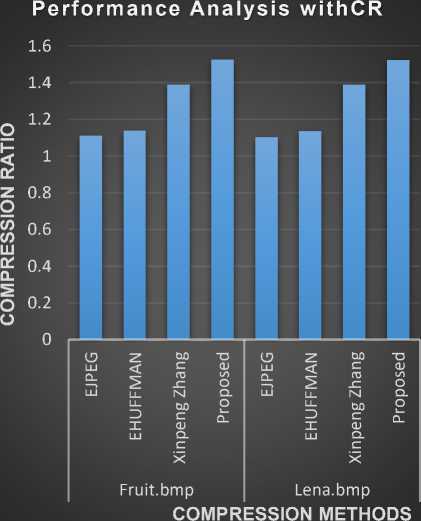
Fig.4. Compression Ratio performance analysis.

Performance Analysis with time consumption

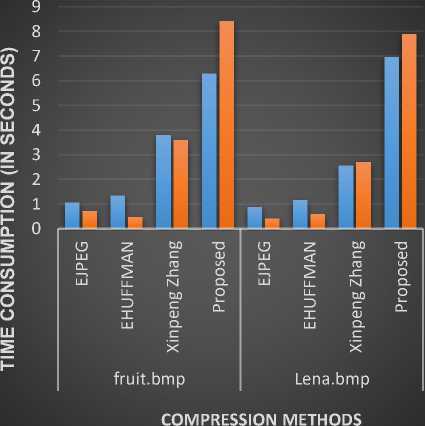
CTT DTT

In Table1, the compression ratio of the proposed system is compared with the existing EJPEG, EHUFFMAN and Xinpeng Zhang methods and the results are plotted in Fig.4. From Table1 and Fig.4, it can be inferred that the proposed method gives better gain in compression ratio. These four CR values are computed against the constant Peak Signal to Noise Ratio (PSNR) value 34.60db. The term CR means Compression Ratio and it is calculated using Equation 12.

CR = 55 °1

BS ri

Where

OI is original image

RI is reconstructed image

BS is byte size

• Fig.5. Time consumption performance analysis.

In Table2 and Fig.5, the time consumption performance of the proposed system is compared with the existing EJPEG, EHUFFMAN and Xinpeng Zhang methods and the results are shown. The time taken for both compression and decompression are little high in the proposed system but it provides better compression ratio and image quality. So, these time taken variations are reasonable and are acceptable. In this table the term CTT represents Compression Time Taken whereas DTT represents Decompression Time Taken.

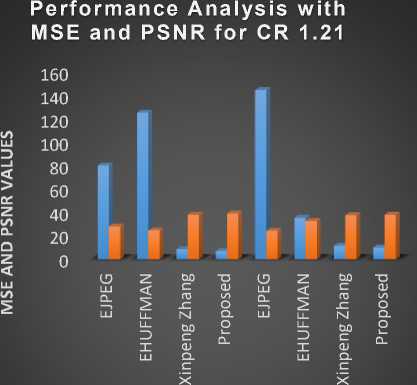
In Table3 and Fig.6, the Mean Square Error (MSE) and PSNR performance measures are taken into account to make the performance analysis. From this table and figure it is proved that the proposed method reaches the lowest MSE and the highest PSNR compared with existing methods. The lowest MSE and the highest PSNR gives higher visual quality. The MSE is calculated using Equation 13 and the PSNR is calculated using Equation 14.

Table 3. Performance analysis with MSE and PSNR for CR value 1.21

Image Name	Algorithm	MSE	PSNR
Fruit.bmp	EJPEG	80.2009	28.0091
	EHUFFMAN	125.4313	24.6009
	Xinpeng Zhang	8.6214	38.0775
	Proposed	6.9726	39.0909
Lena.bmp	EJPEG	144.7417	24.2434
	EHUFFMAN	35.4437	32.6354
	Xinpeng Zhang	11.5098	37.5201
	Proposed	10.0462	38.1108

In Table 4, the Bits Per Pixel (BPP) of the proposed system is compared with the existing EJPEG, EHUFFMAN and Xinpeng Zhang methods and the results are plotted in Fig.7. From Table 4 and Fig.7, it can be inferred that the proposed method gives better gain in BPP. These four BPP values are computed against the constant Compression Ratio (CR) value 1.21. The BPP is calculated using Equation 15.

BPP = 8 / CR                (15)

Where CR is Compression Ration

MSE = ^^₌₁(OI_tJ-RI_t^²      (13)

PSNR = 10 log 10 ( 255 ² / MSE )           (14)

Where

OI is original image

RI is reconstructed image

M is image height

N is image width

COMPRESSION METHODS

MSE PSNR

Performance analysis of Bits Per Pixel

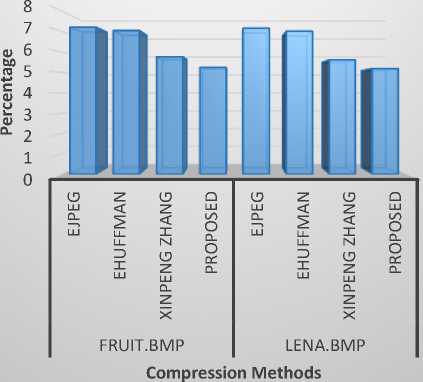
Fig.7. BPP performance analysis

Table 5. Performance analysis with BR for CR value 1.21

Image Name	Algorithm	PR
Fruit.bmp	EJPEG	0.0736
	EHUFFMAN	0.072
	Xinpeng Zhang	0.059
	Proposed	0.053
Lena.bmp	EJPEG	0.070
	EHUFFMAN	0.063
	Xinpeng Zhang	0.055
	Proposed	0.049

Fig.6. MSE and PSNR performance analysis

Table 4. Performance analysis with BPP for CR value 1.21

Image Name	Algorithm	BPP
Fruit.bmp	EJPEG	7.21
	EHUFFMAN	7.043
	Xinpeng Zhang	5.7664
	Proposed	5.25
Lena.bmp	EJPEG	7.16
	EHUFFMAN	7.019
	Xinpeng Zhang	5.62
	Proposed	5.19

In Table 5, the Bit Rate (BR) of the proposed system is compared with the existing EJPEG, EHUFFMAN and Xinpeng Zhang methods and the results are plotted in Fig.8. From Table 5 and Fig.8, it can be inferred that the proposed method gives better gain in BR. These four BR values are computed against the constant Compression Ratio (CR) value 1.21. The BPP is calculated using Equation 16.

BR = RI / (M x N x 3)            (16)

Where

RI is Reconstructed Image M is image height N is image width

Performance analysis of Bit Rate

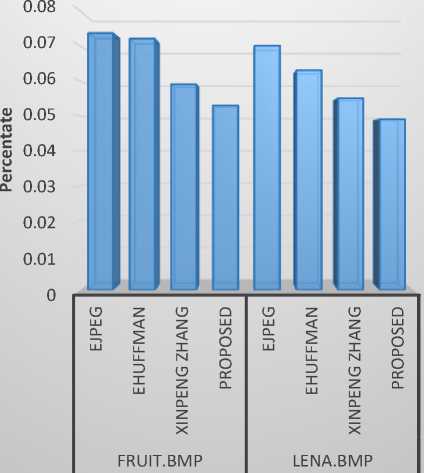
Compression Methods

Fig.8. BR performance analysis

Table 6. Performance analysis with PSSS for CR value is 1.21

Image Name	Algorithm	PSSS
Fruit.bmp	EJPEG	21.95
	EHUFFMAN	22.493
	Xinpeng Zhang	27.486
	Proposed	34.471
Lena.bmp	EJPEG	21.34
	EHUFFMAN	22.03
	Xinpeng Zhang	26.81

In Table 6, the Percentage of Storage Space Saving (PSSS) of the proposed system is compared with the existing EJPEG, EHUFFMAN and Xinpeng Zhang methods and the results are plotted in Fig.9. From Table 6 and Fig.9, it can be inferred that the proposed method gives better gain in PSSS. These four PSSS values are computed against the constant Compression Ratio (CR) value 1.21. The BPP is calculated using Equation 17.

PSSS = 1 – (1 / CR) * 100           (17)

Where CR is Compression Ratio

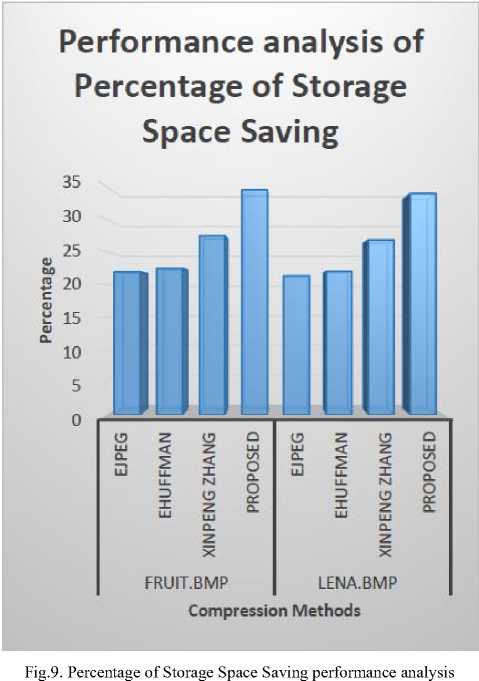
• V. Conclusion

The proposed method aims to compress the encrypted color images. Permutation based encryption is used in this paper. This joint encryption with compression method includes prediction based rigid data encoding, seven bit storage and negative sign removal processes. This paper improves the compression ratio by 9.645%. This method is suitable for image security applications. By considering the overall performance metrics, this paper concludes that the proposed method is better than the existing methods. In future enhancement the seven bit compressed storage can be improved to (n-k) bit compressed storage.