Security against Sample Pair Steganalysis in Eight Queens Data Hiding Technique

Published Online August 2016 in MECS DOI: 10.5815/ijcnis.2016.08.05

The purpose of digital steganography is to conceal information inside a digital cover. A digital cover may be image, maps, audio or video files. The important requirements [7] for any steganographic methods are imperceptibility, capacity, and robustness. However, it is difficult for any steganographic method to simultaneously satisfy all of the three requirements. In the recent years, many steganographic methods are developed in which these steganographic requirements are finely balanced. These methods are mainly divided in two groups: spatial domain [3, 6, 18, 19, 22] and frequency domain [12, 13, 14]. In spatial domain methods, the least significant bit (LSB) embedding are extensively used to hide secret data because it is easy to implement and it offers high embedding capacity. In this approach, raster scans [6, 19] and random scans [18, 20] have been adopted to hide the secret data in the visited pixel. For security concern, the random scan embedding is preferred over the raster scan embedding. Muttoo et al [4, 18] proposed a data hiding method based on eight queen solutions. This method helps in randomizing the bit selection in a cover image for hiding purpose. The hiding methodology is based on hiding relationship between message bytes and 8-queen solutions in the cover rather than the message directly. Kumar et al [22] further proposed data hiding technique based on Inter-Block Difference in Eight Queens Solutions and LSB Substitution. The technique provides a better security and high embedding capacity. Another improved technique based on eight queen solutions is proposed by Bansal et al [3]. The method is based on pixel mapping and eight queens’ solutions for embedding high payload of secret information. Bansal et al [2] also proposed data hiding technique for improving the security in exploiting modification direction method using knight tour in 8 × 8 block of the cover. The method achieves better security using eight queens’ solutions and knight path.

Numbers of steganalysis methods have been developed based on statistical properties of image such as ChiSquare test, RS steganalysis and Sample Pair steganalysis. Fridrich et al [9] proposed RS steganalysis method based on the partition of image pixels into three groups: Regular (R), Singular (S) and Unusable groups (U). Fridrich proposed heuristic assumption that the RS ratio of a natural image should satisfy the certain rule. Dumitrescu et al. [8] proposed analytical proof of an observation made by Fridrich et al. [9]. This method can detect the existence of hidden message that are randomly embedded into the least significant bits of natural images. It is based on state transition among various statistical subsets of an image. Experimental result claims that if the embedding ratio is more than 0.03 bit per pixel then this method is very efficient to estimate the length with relatively high precision. Andrew D. Ker [10] performs statistically accurate evaluation of the reliability of image steganalysis method. It mainly focuses on the RS and SP steganalysis for detection of LSB steganography in natural image and also suggests some improvement. Andrew D. Ker [11] also proposed another LSB based steganalysis technique using structural steganalysis which gives the most sensitive detectors for standard two LSB replacements.

Most of the steganalysis methods discussed above are based on some statistical hypothesis. We need to develop such steganographic systems, which are statistically robust. In this paper, the security strength of data hiding technique [18] are analyzed with respect to a statistical change and then some enhancement are proposed to make the method more secure and robust against various steganalysis.

The paper is organized in seven sections. Sample pair steganalysis is briefly introduced in Section 2. Section 3 describes data hiding technique using eight queen solutions [18]. The Section 4 of this paper deals with the security analysis of data hiding technique based on eight queen solutions and proposed security enhancement. Experimental results are presented in the Section 5. The section 6 presents the steganalysis using STEGEXPOSE tool. Finally, the paper is concluded in the Section 7.

• II.    Sample Pair Analysis

Dumitrescu et al. [20] proposed sample pair steganalysis technique based on statistical assumption to detect LSB steganography in continuous-tone natural image. This assumption is very sensitive to LSB embedding and the change in the identity can quantify the length of the embedding message. In this method, we take P (u, v) as the set of pixel pairs, where u and v are the values of two adjacent horizontal pixel i.e. 0 < u < 2^b –1 , 0 < v < 2^b–1. Here b is the number of bits to represent each pixel in the image. Let D_n be the subset of P that consist of pixel pairs of the form (u, u + n) or (u + n, n), i.e. the two values differ exactly by n, where n is a fixed integer and 0 < n < 2^b–1. Since the embedding effect only the LSB, there is another sub multi-set C_m of P that consists of the pixel pairs whose value differ by m in the first (b –1) bits. For each integer m and 0 ≤ m ≤ 2^{b –1}–1, C m is define as

C m = {(u, v) ϵ P | u/2 – v/2 = m or v/2 – u/2 = m}

Here the multi-sets D_n forms one partition of P and the multi-sets C_m forms another partition of P. It is obvious that D_2m is contained in C_m. In fact if (u, v) is a pair in D_2m then both u and v are either even or odd. But this is not true for D_2m+1. The pixel pairs of D_2m+1 are shared between C_m and C_m+1. We partition D_2m+1 into two multisets X 2m+1 and Y 2m+1 , where

X 2m+1 = D 2m+1 ⋂ C m+1 ,

Y2m+1= D2m+1 ⋂ Cm, for 0 < m < 2b-1-2. Both X2m+1 and Y2m+1 contain pairs (u, v) that differ by 2m+1 (|u-v| = 2m+1). Those pairs with larger even component are in X2m+1 and those with larger odd components are in Y2m+1.

• •    X_2m+1 is the set of pair (u, v) ϵ P such that v is even and u < v, or v is odd and u > v.

• •    Y 2m+1 is the set of pairs (u, v) ϵ P such that v is even and u > v, or v is odd and u < v.

The important statistical assumption proposed for natural image is

|X 2m+1 | ≈ |Y 2m+1 |                   (1)

Table 1. Estimated Length of Hidden Message on Different Natural Image using SP Method

Image	|X 2m+1 |	|Y 2m+1 |	Estimate payload (p)
Lena.bmp	87337	87922	0.0277
Baboon.bmp	94960	94515	-0.0648
Pepper.bmp	84745	87988	0.0484
Pills.tif	91336	90803	-0.0376
Bear.tif	86937	88731	0.0838
Koala.png	92031	92912	0.0954
Fishingboat.bmp	29751	29251	-0.0789
Pentagon.bmp	30427	30929	0.0184

This is because natural images are isotropic in terms of the gradient of intensity function, i.e., the gradient of the intensity function in any direction has equal probability. Based on the above statistical results, the following quadratic equation is derived.

(| Cm | |      | ) _p2    (|     | | ^2пш |)+ 2| ^m+i | "2 | ^2m+i |p

-+ 4                                 2

^| ^2m+l |-| ^2m+l |=0, m ≥ 1           (2)

Here, C m , C m+1 , D 2m and D 2m+1 are different multi-set of P and |*^’| represents the cardinality of the multi-set * in the embedded image. The result p of quadratic equation (2) will estimate the length of the embedded message. The minimum value of p is considered the length of hidden message into the cover. Table 1 shows various statistical results on natural images. It shows that the estimated length of hidden message from equation (2) is approximately zero.

• III.    Data Hiding Approach using 8 Queen’S Solution

Data hiding approach based on eight queen solutions is proposed by Muttoo et al [18] in which 8-queens solutions are extracted by placing 8 non-attacking queens on 8 × 8 chessboard. In 8 × 8 chessboard, the number of distinct 8 queens’ solutions is 92 [17, 21]. The proposed approach utilizes the feature of 92 different patterns on 8 × 8 block by matching with the secret message. In this procedure, the cover image is divided into blocks of 8x1 bytes and then block is masked with different solutions of the 8-queens problem. Bits from the block are collected corresponding to the 8-queen solution to make a 7 bit string, which gives a number in the range of 0 to 127. If a bit string, corresponding to the 8-queens solutions, matches with ASCII code of the first character from message, the corresponding solution number of the 8-queens problem is encrypted using RC4, and the cipher is stored in first block of the cover. This encrypted value works as key. The solution number corresponding to next character is XORED with the key and the resultant value is embedded in the LSB of next block.

In this method, the hiding methodology is based on the hiding relationship between message bytes and 8-queen solutions rather than the message directly. This method also helps in randomizing the bit selection in a cover image for hiding purpose. The goal of this method is to embed secret message in such a way that the detection of secret message becomes difficult.

In the proposed approach, we analyzed the detection of the existence of the hidden message in the stego image using sample pair steganalysis. Table 2 shows the estimated length of hidden message on different stego image. It shows that the length of hidden message is near to payload of the stego image. Thus, we require some enhancement of the method in order to make it more secure and robust against the SP steganalysis method.

• IV.    Security Analysis

We have proposed improvement and undetectablity of data hiding technique based on eight queen solutions [18]. As illustrated in section 2, the principle of SP steganalysis method is based on the assumption that

|X 2m+1 | ≈ |Y 2m+1 |

It is based on statistical characteristic of the cover. The statistical characteristic is the cardinalities of the set C m , D 2m , X 2m+1 and Y 2m+1 . For each modification pattern π ϵ {00, 10, 01, 11}, the statistical characteristic are modified with pattern π as a result of embedding. This modification changes the statistical characteristic of the cover image and it is measured using equation (2).

Table 2. Estimated Length using Sample Pair Steganalysis on Various Stego Images of Different Payload (γ)

Payload	γ = 0.1			γ = 0.2			γ = 0.3
Image	|X 2m+1 |	|Y 2m+1 |	Estimate Length	|X 2m+1 |	|Y 2m+1 |	Estimate Length	|X2m+1|	|Y2m+1|	Estimate Length
Baboon.bmp	94202	95122	0.1293	93654	95524	0.2553	92660	95518	0.2537
Lena.bmp	85996	88491	0.1128	84852	89265	0.1933	84080	89674	0.2529
Pepper.bmp	84745	87998	0.1353	83504	88711	0.2094	82799	89130	0.2488
Pills.tif	90620	91359	0.0513	89689	91934	0.1593	89340	92521	0.2102
Bear.tif	86346	89075	0.1261	85941	89420	0.1589	85098	89998	0.2154
Koala.png	91680	93456	0.1651	91224	94247	0.2447	90421	94553	0.3256
Pentagon.bmp	30427	30929	0.1274	30260	31069	0.2037	30063	31229	0.2882
Fishingboat.bmp	29285	29556	0.0519	29071	29789	0.1542	28496	30333	0.2847

The simple method to avoid statistical modification is to ensure no embedding in the adjacent pixel pairs that differ in their value by less than 3. However, this method is open to attack because of known locations. Luo et al. [15] proposed a LSB approach against pixel pair steganalysis method in which the adjustment of statistical characteristic is based on compensation algorithm. The compensation algorithm finds adjacent pixels pair such that difference of their value is 2m+1, where 0 ≤ m ≤ 2b-1–1 and b is the number of bits to represent each pixel. Then half stego image is added by 1 for adjustment of statistical change after embedding. Here the compensation area can be chosen at will. Therefore, the sender and receiver must have the knowledge about the locations of the pixel in the image where pixel value is added by 1 so that message can be extracted at the receiver end. This is the main drawback of this approach.

In this paper, we present a noble approach to adjust the statistical properties of a cover image in order to increase robustness against SP steganalysis. We also present an additional security layer to enhance security and privacy of the embedded message.

• A.    Robust Hiding Method

In the proposed method, cover image is divided into two groups of 8 × 1 pixel blocks. The first group of 8 × 1 pixels block is used to hide secret information and the second group contains no secret information. In order to improve the security strength of the hiding algorithm, the second group is utilized to modify the pixel in such a way that the statistical property |X 2m+1 | and |Y 2m+1 | of stego image remains as similar as that of cover image. Therefore, the estimated length of hidden information by SP steganalysis is near to zero. The experimental results shown in Table 2 shows that the value of |Y 2m+1 | is higher than |X_2m+1|. Thus, the result of estimated length of hidden information in stego image is near to the payload in the cover.

The assumption 1 on natural image implies that the gradient in any direction of natural image has equal probability. Therefore, we need to adjust such pair in which odd components is larger i.e., decrease the cardinality of Y2m+1. Enhancement to this algorithm is discussed in this paper to to make the approach secure and robust.

Let P (ui, vi) be sample pair of two horizontal adjacent pixels. The sample pair to be modified, should satisfy the condition |ui – vi | < δ, where δ is threshold value. Let αm = |Y2m+1| – | X2m+1|, where 0 ≤ m ≤ 2b-1–2 and b be the number of bits to represent a pixel in the cover. We need to decrease the cardinality of Y2m+1 in order to make this value almost equal to the cardinality of X2m+1. Here, Y2m+1 is the set of pair (ui, vi) ϵ P such that v is even if u > v, or v is odd if u < v.

In this approach, we consider sample pair P(ui, vi) in which vi is odd, ui < vi, and | ui – vi | < δ. Further, we increase the value ui where, ui < (255 – δ) as ui = ui + | ui – vi | + 1

thus making u_i > v_i in the sample pair P (u_i, v_i). However, v_i remains odd therefore, the cardinality of Y_2m+1 decreases by one, while the cardinality of X_2m+1 increases by one. To satisfy assumption 1, we need to modify at least (α m /2) sample pairs in the cover image. The stepwise procedure is given below.

• B.    Algorithm to enhance robustness

Step 1: Embed the secret message using the proposed method and take a threshold value δ.

Step 2: Find statistical properties of |X_2m+1| and |Y_2m+1| using sample pair steganalysis and calculate α ₌ ((|Y 2m+1 | – |X 2m+1 | ) / 2), where 0 ≤ m ≤ 2^b-1–2, here b is number of bits to represent pixel in the cover.

Step 3: Find 8 × 1 pixel block, which does not contain secret message, and make sample pair with their adjacent pixel such as (u i ,v i ), where u i is i^th pixel value of 8 × 1 block and v i is the horizontal right adjacent pixel of u i, here i = 1, 2,....8

Step 4: Let x=1

Step 5: In each 8×1 pixel block, starting form second block, for sample pair (ui, vi), i = 2,3,4,...8 do the following

If (mod (vi, 2) = = 1) and ui < vi then di = |ui – vi| If di < δ and u < (255 – δ) do the following

Find r = u_i + (d_i + 1) u i = r x = x + 1

Step 6: While x < α, repeat step 5 for next pixel block Step 7: Find the statistical properties of |X 2m+1 |, |Y 2m+1 | and estimate hidden message length p in the stego image.

Step 8: If p ≥ 0.07 then calculate β = ||Y2m+1| – |X2m+1| | / 2

Step 9: α = α + β and go to step 4

• C.    Resuhuffling of 8queen’s solution array

The security of data hiding approach using eight queen solutions [18] depends on RC4 encryption. Once the RC4 encryption is cracked, the secret message can be revealed. An 8-queen problem has 92 solutions. All solutions are stored in two dimensional arrays Q of size 92×8. The solutions of eight queen problem are stored in an array Q as shown in Figure 1. Each character C from message M is compared with 7 bit string from Q. If a match is found, then solution number corresponding to next character is XORED with the key and the resultant value is embedded in the LSB of corresponding 8×8 bits block. First character of M is compared with 92 solutions from Q. If a match id found then the solution number is considered as a key. It means the key should be any one number from 1 to 92. It can be easily detected by brute force method. For a high security, we propose the new concept to reshuffle the array of eight queen solutions using key scheduling algorithm for each block.

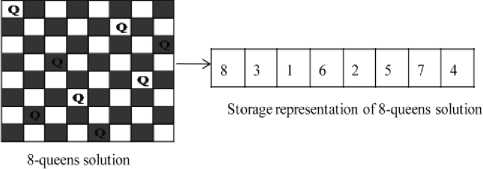
Fig.1 Storage Representation of Eight Queen Solutions

In the key scheduling algorithm (KSA), the array Q is reshuffled with the stego-key [1]. A variable length stego key between 40 to 92 bits is used to initialize a 92-byte state vector S that contains a permutation of all solutions of eight queens’ problem. S is initialized with values from 0 to 91 in ascending order i.e., S[0] = 0, S[1] = 1, S[2] = 2, ...., S[91] = 91. Let T be a temporary vector. If the length of key K is 92 bits then S is transferred to T, otherwise length l of key is used to initialize T as below:

For i= 0 to 91 do

S[i] = i;

T[i] = S[i mod l];

Then temporary vector T is used to produce the permutation of S as below:

j = 0

For i = 0 to 91 do j = (j + S[i] + T[i]) mod 92

Swap (S[i], S[j])

After this swap, S still contains solutions number from 0 to 91 of all the solutions of eight queens’ problem but in different order. This approach is more secure because array Q is reshuffled for each block. Therefore even if RC4 encryption is cracked, the secret message cannot be retrieved without knowing the stego key.

• V.    Experimental Result

Standard cover images and corresponding stego images are presented in Figure 2. We observe that there is no visual difference due to embedding and adjustment of statistical properties in the cover. We carried out experiments with hundreds of never compressed test images from image_database / All of these test images were converted to 256 × 256 pixels size. To assess the visual quality of an image after embedding, we used the Peak-Signal-to-Noise Ratio (PSNR) as the measure of distortion due to data hiding. The PSNR is defined as follows:

(c)

PSNR = 10 x log -55- dB ,

MSE

MSE =

MSE R + MSE G + MSE_b

M - 1 N - 1

MSEr = ^^ ( X r ( i , j ) - 1 ' r ( i , j ))^- i = 0 j = 0

(d)

where, X(i, j) and I’_r(i, j) represent the values of the pixel at location (i, j) in the original image and the stego image respectively. M and N represent height and width of the images respectively. The PSNR value of greater than 30 dB is considered as safe value for retaining the similarity between cover and stego images. In this case, it is hard to distinguish stego images from its corresponding cover image through human eyes. We used MATLAB 9.0 to test the result.

(e)

(f)

(a)

(b)

(g)

Fig.2. Cover image and stego image after adjustment of statistical properties at different embedding rate (γ). (a) Baboon.bmp and Stego image at γ = 0.50 (b) Lena.bmp and Stego image at γ = 0.40 (c) Peppers.bmp and Stego image at γ = 0.40 (d) Pills.png and stego image at γ = 0.30 (e) Bears.tif and stego image at γ = 0.30 (f) Koala.tif and stego image at γ = 0.30 (g) Fishingboat.bmp and stego image at γ = 0.30 (h) Pentagon.bmp and stego image at γ = 0.20

We performed statistical analysis using SP steganalysis method on thousands of 24-bit colour and greyscales images. We calculated various statistical properties like |X 2m+1 |, |Y 2m+1 | and estimated payload using sample pair method on different stego images. Some of the results are shown in Table 3.

(h)

Table 3. Sample Pair Statistical Properties of Different Stego Images at Threshold δ = 4

	Threshold δ = 4
Image	γ = 0.1			γ = 0.2			γ = 0.3
	|X 2m+1 |	|Y 2m+1 |	Estimate Payload	|X 2m+1 |	|Y 2m+1 |	Estimate Payload	|X 2m+1 |	|Y 2m+1 |	Estimate Payload
Baboon.bmp	94478	94888	0.0584	94418	94849	0.0606	94407	94788	0.0530
Lena.bmp	87614	87107	-0.0235	87462	86978	-0.0221	87273	86995	-0.0126
Pepper.bmp	85666	87179	0.0640	85864	86675	0.0640	85483	86620	0.0466
Pills.tif	90795	91195	0.0277	90483	91169	0.0478	90419	91283	0.0586
Bear.tif	87086	88395	0.0617	86909	88168	0.0647	86980	88319	0.0624
Koala.png	92609	92961	0.0325	92466	92970	0.0459	92471	93053	0.0658
Cat.png	93533	94128	0.0681	93532	94130	0.0684	95536	94126	0.0675
Fishingboat.bmp	29507	29358	-0.0233	29379	29494	-0.0185	29311	29665	0.0602
Pentagon.bmp	30557	30800	0.0618	30524	30771	0.0618	30502	30768	0.0649

Table 4. PSNR and Embedding Capacity γ (bit per pixel) of Different Stego Image at Threshold δ = 4

Image	PSNR
	γ = 0.1	γ = 0.2	γ = 0.3
Baboon.bmp	55.6808	52.5865	50.6873
Lena.bmp	54.3215	51.8932	50.0591
Pepper.bmp	54.9350	51.8206	50.0856
Pill.tif	55.2498	52.1032	50.3628
Bear.tif	55.4763	52.2163	50.0110
Koala.png	55.0589	52.2713	50.5242
Fishingboat.bmp	55.1575	52.0292	50.3214
Pentagon.bmp	55.2511	52.1171	50.6722

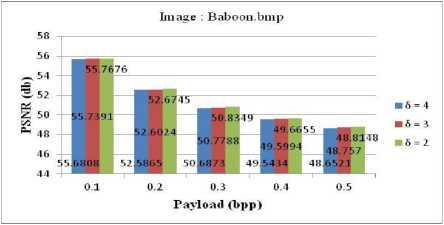
The experimental results show that the statistical properties |X 2m+1 | and |Y 2m+1 | are near to each other and the estimated payload p is below 0.07 of length of hidden message. The SP steganalysis fails to detect presence of hidden information in the cover image. The PSNR results shown in Table 4 confirm that the imperceptibility level of stego image is within acceptable range. The proposed method is tested on different threshold values δ. By comparing the value of PSNR v/s payload for threshold δ

= 2 to 4 as shown in Figure 3, it is observed that the result of threshold δ = 2 are slightly better than others threshold.

• VI.    Steganalysis

We used STEGEXPOSE [5] – a steganalysis tool. It is basically based on the fusion technique that consists of popular steganalysis methods: RS analysis, SP analysis, chi-square attack and difference histogram analysis. The experimental results obtained using STEGEXPOSE tool on various stego images of proposed approach are shown in Figure 4. The estimated length of hidden message is below 0.07 for different embedding capacity. Therefore, the proposed method is robust against SP steganalysis and STEGEXPOSE tools.

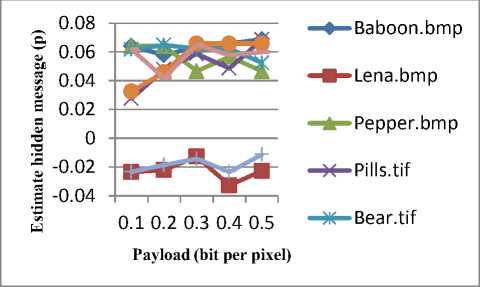
Fig.4. Payload Vs Estimated Length (p) of Hidden Message

• VII.    Conclusion

In this paper, we discussed the security of data hiding method based on eight queen solutions and its improvement on two different aspects. We analyzed the detection of the existence of the hidden message using sample pair steganalysis and then we proposed enhancement in order to achieve robustness in hiding techniques against sample pair steganalysis. We analyzed the strength of data hiding approach with respect to security and then suggested a new security layer by reshuffling the array of eight queen solutions for each block based on stego-key. The experimental results show that the estimated length of hidden message after adjustment of statistical properties is near to zero. The proposed method is secure and robust against detection of secret message. Some experiments were carried to indentify the maximum payload in a cover and found that the embedding capacity is almost 0.5 bit per pixel on different image. This corroborates that there exists a trade-off between capacity and undetectablity. We will test this approach with other steganalysis tools/methods to improve undetectablity of secret information.

Acknowledgment

We are very grateful to all those who have been constantly encouraging and providing required resources for such scientific research work besides the regular work which we are doing in our respective departments. We are grateful to our colleagues and seniors for their continuous support and encouragements and to all those who provided suggestions for improvement of this work. We are thankful to Jessica Fridrich, who supplied the SP steganalysis code on her website http://dde.binghamton. edu/download/structural_lsb_detectors.