Security Analysis and Implementation of an Improved Cch2 Proxy Multi-Signature Scheme

Published Online March 2014 in MECS DOI: 10.5815/ijcnis.2014.04.06

• I.    INTRODUCTION

  Elliptic curve cryptosystem was introduced by Koblitz [1] and Miller [2] in 1985. The attractive public key cryptosystem is ECC because ECC has shorter key size and faster computing speed. The public key cryptosystem’s security is based on the relative complexity of the mathematical problem. For example, the security of RSA depends on integer factorizing problem and the security of DSA depends on discrete logarithm problem [10]. ECC is developed by integer points over elliptic curves in finite fields. The security of ECC is based on the difficulty of solving the elliptic curve discrete logarithm problem (ECDLP).When one person needs to delegate his/her signing capability to other party or person, the proxy signature is very useful tool. In 1996, Mambo et al.’s [3] introduced first proxy signature scheme. Proxy signature is a signature scheme which allows one party called original signer to delegate his/her signing capability to another party called Proxy signer and then on behalf of the original signer, proxy signer can create signature on messages and after signature creation, proxy signer sends these signatures to the verifier and then verifier verify these signatures. Yi et al.’s [6] presented proxy multi-signature scheme which enables one proxy signer to create signature on behalf of group of original signers.

Various security definitions:

A proxy signature should have security properties [4] and they are:

• 1.    Strong Unforgeability: Only designated proxy signer can create proxy signatures. Original signer or any other party cannot create proxy signatures.

• 2.    Verifiability: A verifier can be convinced of the original signer’s agreement on the signed message from the proxy signature.

• 3.    Strong Identifiability: From the proxy signature, anyone can determine the identity of corresponding proxy signer.

• 4.    Strong Undenability:  once valid proxy

• 5.    Distinguishability: Proxy signatures that are created by proxy signer are distinguishable from ordinary signatures that are created by original signer.

signature is created by proxy signer for an original singer, he/she cannot repudiate signature creation.

Various attacks:

• •    Public key substitution attack: By updating his/her own public key, an attacker can forge a valid proxy multi-signature [7].

• •    Original signer’s forgery attack: Without agreement of proxy signer, original signers can create proxy multi-signature. Verifier will be sure that any proxy multi-signature created by using forged signing key are created by agreement of all original signers and proxy signer [15]. Under the name of proxy signer, original signer can forge valid proxy multisignature.

• •    Transferring attack: In this attack, proxy signer’s standard schnorr signature can be converted into proxy signature in which signer is regarded as proxy signer by the verifier and vice versa [13].

• •    Framing attack: In this attack, any user P can be framed by malicious users A 1, A 2 ...A n . User P does not receive any delegation from the users A_1, A₂...A_n, but the malicious users A_1, A₂...A_n can forge a proxy multi-signature for message by user P on behalf of users A 1, A 2 ...A n [16].

Mambo et al.’s [3] introduced different types of delegations i.e. full delegation, partial delegation and delegation by warrant. In full delegation, the original signer gives his/her own secret key to proxy signer, so that proxy signer can create same signature as original signer creates. In partial delegation, a proxy signer has proxy private key, which is different from original signer’s private key and proxy signer can sign range of messages in partial delegation because delegation period is not specified. In delegation by warrant, warrant is added that specifies what kinds of messages are delegated, the delegation period, IDs of original signers and proxy signer etc. According to protection of proxy signer, partial delegation is further divided as proxy-unprotected and proxy-protected. In proxy unprotected, the original signer gives proxy signing key to the proxy signer and proxy signer create signature by using that key. So, in proxy unprotected proxy signature the original signer knows the proxy signing key and he/she can also create the same proxy signatures. In proxy protected, the proxy signer compute proxy signing key from his/her owns private key and the key given by original signer and then generates proxy signature. So in proxy protected proxy signature any third party including the original signer cannot create the same proxy signatures. In partial delegation, the signing capability of the proxy signer can be revoked by the original signer by two ways i.e. (1) Prepare revocation list and make it publicly seen. (2) The public key of original signer can be changed and accordingly all proxies of sincere proxy signers are updated. M. Mambo, K. Usuda, and E. Okamoto [4] have introduced proxy protected proxy signature scheme based on discrete logarithm problem. S. Kim, S. Park, and D. Won [5] have introduced two new types of proxy signature schemes i.e. proxy signature for partial delegation with warrant and proxy signature for threshold delegation. Partial delegation with warrant combines the benefits of partial delegation and delegation with warrant. H. M. Sun [7] analyzes Yi et al.’s [6] proxy multi-signature schemes and show that these schemes are suffered from public key substitution attack and direct forgery attack. They introduced a new proxy protected and proxy unprotected proxy multi-signature schemes which do not suffered from these attacks. B. Lee, H. Kim, and K. Kim [8] develop a strong non-designated proxy signature scheme and apply it to multi-proxy signature in which multiple original signers can delegate his signing capabilities to undetermined proxy signers. T. S. Chen, T. P Liu, and Y. F Chung [9] introduced a proxy protected proxy signature scheme based on elliptic curve discrete logarithm problem. On the basis of time complexity, they compare H. M. Sun [7] and the proposed scheme. T.S. Chen, Y.F. Chung and G.S. Huang [10] introduced an improved scheme in which the exponential operations are replaced by elliptic curve multiplicative ones. ECC with lower computational overhead and a smaller key size can achieve a level of security equal to that of the RSA or DSA. This proposed scheme is called CCH1 scheme. Without loss of security, the time complexity of proposed scheme is reduced and performance is enhanced. T.S. Chen, Y.F. Chung, G.S. Huang [11] introduced a traceable proxy multi-signature scheme. This proxy signature scheme is independent of number of original signers so, number of operations required for verification decreases. This proposed scheme is called CCH2 scheme. On the basis of time complexity they compare the sun’s [7] and proposed proxy multi-signature scheme. M.S. Hwang, S.F. Tzeng and C.S. Tsai [12] introduced a generalized version of the (t1/n1-t2/n2) proxy signature scheme based on elliptic curve discrete logarithm problem. G. L. Wang, F. Bao, J. Y. Zhou, and R. H. Deng [13] analyze the security of some proxy signature schemes i.e. M. Mambo et al.’s [4] and B. Lee et al.’s [8] and show that all these schemes are suffered from various attacks. S. Wang, G. Wang, F. Bao and J. Wang [14] shows that chen et al.’s [9] is  vulnerable to an original signer forgery attack and introduced an improved scheme which is secure against the proposed attack. J.H. Park, B.G. Kang, S. Park [15] shows that proxy multisignature schemes proposed by Chen et al.’s [10, 11] are vulnerable to forgery attack by one or all original signers. M.H. Chang, I.T. Chen and M.T. Chen [17] presented a proxy protected signature scheme based on ECDSA which satisfies security properties. Fengying Li, Qingshui Xue [18] proposed improved CCH1 and improved CCH2 schemes that are not suffered from forgery attack. Tutanescu, C. Anton, L. Ionescu and D. Caragata [19] examines that ECC is an attractive public key cryptosystem than RSA or DSA for mobile devices, which have limited memory, processing capability and network connectivity. ECC can be implemented with less hardware, because of shorter key length. They have defined the application of ECC i.e. internet, smart cards, PDAs and PCs.

• II. TIME, SPACE AND COMPUTATIONAL OVERHEAD OF IMPROVED CCH1 AND IMPROVED CCH2 PROXY MULTI-SIGNATURE SCHEME

• A.    Review of improved CCH1 proxy multi-signature scheme

There are four phases––Initialization phase, key generation phase, proxy multi-signature generation phase and proxy multi-signature verification phase [18].

Phase 1: Initialization phase over the elliptic curve domain following parameters must be known.

• >    A field size p, which is odd prime.

• >    Two parameters U^Jpp to define the equation of elliptic curve E over Fp (i.e., y2 = x3 + ax + b (mod p)), where 4a3 + 27 b2 ≠ 0 (mod p)

• >    A finite point B = (xB,yB) whose order is a large prime number in E(Fp), where B is a point in E(Fp). Where B ≠ O, because O denotes an infinity point.

• >    The order of B = t.

Phase 2: Key generation phase: This phase is further divided into two parts.

Part 1: Personal key generation phase: All original signers and the designated proxy signer select their own individual secret keys.

• •    For each 1≤ i ≤n, the original signer A_i secretly selects a random number 1≤ d_i ≤ t – 1 as his private key, and computes the corresponding public key Q i = d i × B = (x Q , y Q ), where “×” indicates the multiplication of a number and elliptic curve point.

• •    The proxy signer is provided with a private key 1≤ d p ≤ t – 1 and a corresponding public key Q p = d p ×B = (x Qp , y Qp ) .

Part 2: Proxy-signature secret key generation phase:

Step 1 : (Secret key generation): For each 1≤ i ≤n, the original signer A i selects a random number k i {1, 2… t– 1}/ d i as secret key.

Step 2 : (Group commitment value generation): Then computes

R i = k i × B = (x Ri ,y Ri )                        (1)

If xRi =0 then return to step 1; otherwise Ai gives Ri to other original signers.

Step 3 : (Sub-delegation parameter generation): For each 1≤ i ≤n, the original signer A i uses his own secret keys d i , k i and the group commitment value x R to compute the following:

s i = d i * x Q _i* h(M w , R i ) – k i *x R _i (mod t)      (2)

Where h ( ) is a hash function and the warrant Mw contains information such as the IDs of all original signers and proxy signer. Then, the sub-delegation parameter for Ai is (Mw,Ri, si).

Step 4 : (Sub-delegation parameter verification): After the proxy signer has received the subdelegation parameters then the proxy signer P computes

S i ×B= (x Q _i *h(M w ,R i ) )*Q i –x R _i R i            (3)

and check whether it holds. If it holds then the proxy signer accepts (M_w,R_i,s_i) as a valid subdelegation parameter; otherwise, he can reject it and requests a valid one A i , or terminate this protocol.

Step 5 :( Proxy multi-signature secret key generation): Then computes the proxy multi-signature secret key as follows:

d = dp* xQp +∑ni=1si mod t              (4)

Phase 3: Proxy multi-signature generation phase: The proxy multi-signature is in the form of (m, mw, R,

Sigd(m)), where Sigd(m) is the signature generated by a designated signature scheme (EC-schnorr signature scheme) using the proxy signing key d and m is message.

Step 1 : Proxy signer P choose random number j where 1≤ j ≤ t– 1 and calculate J = j × B = (J x ,J y ).

Step 2 : Compute e= h(m, J_x) where h(J_x, m) is hash function. If e = 0 then go to step 1.

Step 3: Compute y = j - d * e (mod t)                          (5)

and the output sign d (m) = (e,y).

Phase 4: Proxy multi-signature verification phase: When the verifier verifies the signature, he or she calculates the proxy public value Q corresponding to the proxy signature key d as

Q= Q P * x Q _p+ ∑ⁿ  (h(M w , R i ) *Q i –x R _i × R i )         (6)

With the value, the verifier can confirm the validity of Sig d (m) by validating the verification equality of the designated signature scheme.

Step 1 : Compute J̅ = y × B + e × Q = (J̅_x,J̅_y)

Step 2 : And compute e´ = h (J̅ _x,m) . Then check that e´ = e and if these are equal then valid signature otherwise not.

• B.    Review of improved CCH2 proxy multi-signature scheme

There are four phases––Initialization phase, key generation phase, proxy multi-signature generation phase and proxy multi-signature verification phase [18].

Phase 1: Initialization phase: Over the elliptic curve domain following parameters must be known.

• >    A field size p, which is a odd prime.

• >    Two parameters a, b Fp to define the equation of elliptic curve E over Fp (i.e., y2 = x3 + ax + b (mod p)), where 4a3 + 27 b2 ≠ 0 (mod p)

• >    A finite point B = (xB, yB) whose order is a large prime number in E(Fp) , where B is a point in E(Fp). Where B ≠ O, because O denotes an infinity point.

• >    The order of B = t.

Phase 2: Key generation phase: This phase is further divided into two parts:

Part 1: Personal key generation phase: All original signers and the designated proxy signer are authorized to select their own individual secret keys.

• •    For each 1≤ i ≤n, the original signer A i secretly selects a random number 1≤ d_i ≤ t – 1 as his

private key, and computes the corresponding public key Q_i = d_i × B = (x Q , y Q ), where “×” indicates the multiplication of a number by an elliptic curve point.

• •    The proxy signer is provided with a private key 1≤ d p ≤ t – 1 and a corresponding public key Q p = d p ×B = (x Qp , y Qp ) . All public keys Q i and Q p must be certified by the CA.

Part 2: Proxy-signature secret key generation phase:

Step 1 : (Secret key generation): For each 1≤ i ≤n, the original signer A i selects a random number k i {1, 2… t– 1}/ d i as secret key.

Step 2: (Group commitment value generation): Then computes Ri = ki × B = (xRi , yRi). If xRi =0 then return to step 1; otherwise Ai broadcasts Ri to other original signers. On receiving Rj (1 ≤ j ≤ n, j ≠ i), Ai calculates i = (xR,yR)                                      (7)

Step 3 : (Sub-delegation parameter generation): For each 1≤ i ≤n, the original signer A_i uses his own secret keys d_i, k_i and the group commitment value x R to compute the following.

s i = d i * h(M w , x Qp ,x Qi , x R ) – k i * x R (mod t) (8)

Where h ( ) is a hash function and the warrant Mw contains information such as the IDs of all original signers and proxy signer. Then, the sub-delegation parameter for Ai is (Mw,si).

Step 4: (Sub-delegation parameter verification): After the proxy signer has received the subdelegation parameters then the proxy signer P computes si * B= h(Mw, xQp ,xQi , xR) *Qi – xR × Ri checks whether it holds. If it holds then the proxy signer accepts (Mw,si) as a valid subdelegation parameter; otherwise, he can reject it and requests a valid one Ai , or terminate this protocol.

Step 5 :( Proxy multi-signature secret key generation): Then computes the proxy multi-signature secret key as follows:

d = dp +     i mod t                   (10)

Phase 3: Proxy multi-signature generation phase: The proxy multi-signature is in the form of (m,mw,R,Sigd(m)) , where Sigd(m) is the signature generated by a designated signature scheme (EC-schnorr signature scheme) using the proxy signing key d and m is message.

Step 1 : Proxy signer P choose random number j where 1≤ j ≤ t– 1 and calculate J = j × B = (J_x, J_y).

Step 2 : Compute e= h(m, J x ) where h(J x , m) is hash function. If e = 0 then go to step 1.

Step 3: Compute y = j - d × e (mod t)                        (11)

and the output signd(m) = (e,y).

Phase 4: Proxy multi-signature verification phase: When the verifier verifies the signature, he or she calculates the proxy public value Q corresponding to the proxy signature key d as

Q= Q P + (M w , x Qp , x Qi , x R ) × Q i – R × x R     (12)

With the value, the verifier can confirm the validity of Sig d (m) by validating the verification equality of the designated signature scheme.

Step 1 : Compute J̅ = y × B + e × Q = (J̅_x,J̅_y)

Step 2 : And compute e´ = h (J̅_x,m). Then check that e´ = e and if these are equal then valid signature otherwise not.

• C.    Time, Space and Computational overhead of improved CCH1 and CCH2 scheme

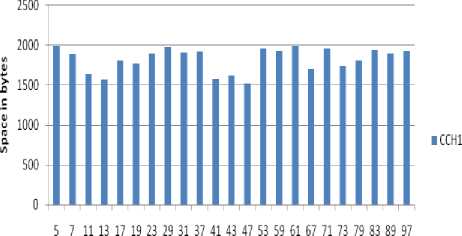
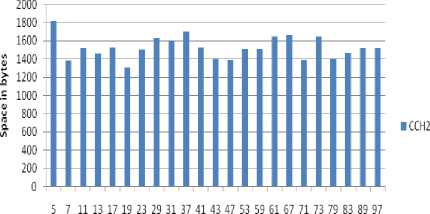
This table shows the time, space and computational overhead of improved CCH1 and CCH2 proxy multisignature scheme with varying value of field size (p).

TABLE NO. 1 Time, space and computational overhead of improved CCH1 and CCH2 scheme

Sr. No	p	Time complexity		Space complexity		Computational overhead
		CCH1	CCH2	CCH1	CCH2	CCH1	CCH2
1.	5	1724	1549	1994	1810	211	175
2.	7	1619	1358	1894	1379	208	177
3.	11	1786	1369	1641	1515	210	180
4.	13	1503	1494	1565	1459	211	168
5.	17	1583	1426	1813	1524	210	171
6.	19	1777	1461	1774	1308	211	169
7.	23	1728	1572	1905	1505	218	177
8.	29	1761	1456	1979	1629	212	187
9.	31	1748	1448	1914	1602	213	170
10.	37	1590	1419	1918	1700	203	184
11.	41	1510	1407	1576	1524	213	187
12.	43	1535	1516	1624	1405	215	175
13.	47	1745	1359	1517	1387	204	168
14.	53	1539	1350	1963	1506	203	182
15.	59	1613	1431	1934	1508	215	172
16.	61	1624	1421	1987	1644	208	181
17.	67	1581	1350	1695	1661	217	170
18.	71	1636	1340	1964	1391	216	183
19.	73	1667	1391	1744	1648	217	175
20.	79	1779	1418	1813	1405	214	185
21.	83	1554	1363	1943	1464	208	173
22.	89	1583	1575	1904	1515	209	176
23.	97	1553	1438	1927	1517	219	184

• D.    Graphical representation of Time, Space and Computational overhead of improved CCH1 and CCH2 scheme

Graphs shows the time, space and computational overhead of improved CCH1 and CCH2 proxy multisignature scheme with varying value of field size (p).

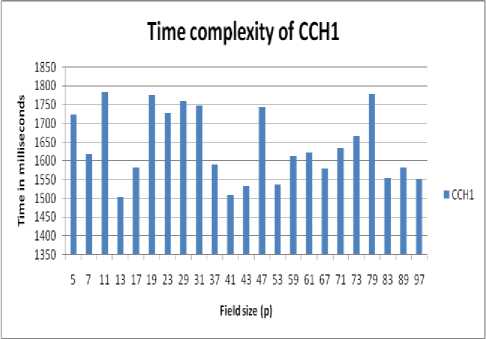
Figure. No. 1 Time complexity of improved CCH1 scheme with varying value of field size (p)

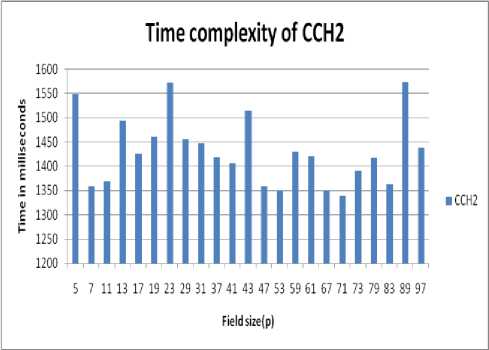
Figure. No. 2 Time complexity of improved CCH2 scheme with varying value of field size (p)

Space complexity of CCH1

Fieldsize(p|

Figure. No. 3 Space complexity of improved CCH1 scheme with varying value of field size (p)

Space complexity of CCH2

Field size(p)

Figure. No. 4 Space complexity of improved CCH2 scheme with varying value of field size (p)

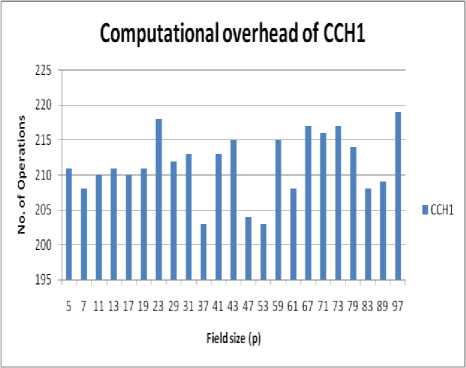
Figure. No. 5 Computational overhead of improved CCH1 scheme with varying value of field size (p)

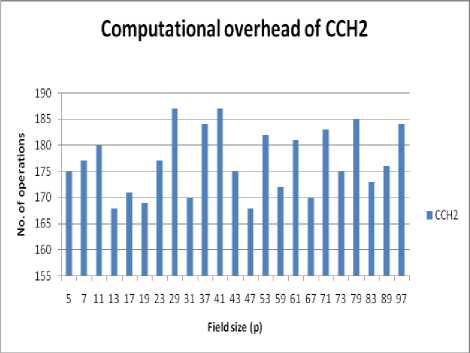
Figure. No. 6 Computational overhead of improved CCH2 scheme with varying value of field size (p)

• III. CRYPTANALYSIS OF IMPROVED CCH2 PROXY MULTI-SIGNATURE SCHEME

Elliptic curve based schnorr signature scheme is used in improved CCH2 proxy multi-signature scheme to generate and verify the signature.

• A.    Forge a proxy multi-signature

Suppose proxy signer P signed a message with his private key dp and the signature that are generated is (m, mw, R, e, y´´) where e= h(m, jx) and y´´ = j-dp *e (mod t). Upon received the signature (m, mw, R, e, y´´) the malicious original signers A1…An can forge proxy signature by computing following operations:

• •    Compute y´=    i s i * e mod t.

• •    Compute y= y´´ - y´

Finally, the malicious original signers A1…An can forge proxy signature (m, mw, R, e, y). The following proof shows that why the proxy signature (m, mw, R, e, y) is valid.

PROFF:

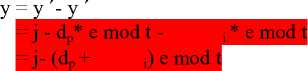
y = j – d*e mod t

Proxy multi-signature verification: When the verifier verifies the signature, he or she calculates the proxy public value Q corresponding to the proxy signature key d as

Q= Q_P+       (M_w, x Q _p, x Q _i , x_R) × Q_i – R × x_R     (13)

Then, the verifier can confirm the validity of Sigd (m) by validating the verification equality of the designated signature scheme.

Step 1 : Compute J̅ = y × B + e × Q = (J̅_x,J̅_y)

Step 2 : And compute e´ = h (J̅ x ,m) . Then check that e´ = e and if these are equal then valid signature otherwise not.

• B.    Forge the proxy signer’s signature

After getting signature (m,mw,R,e,y) that are generated by proxy signer on behalf of original signers Where e= h(m, jx) and y = j-d*e (mod t), the original signer A1…An can forge proxy signer P’s signature on message m by computing following opeartions:

• •    Each A i compute s i * e where i=1,2,..n.

• •    Compute y´= ^^i^— i s_i *e mod t.

• •    Compute y´ = y + y´.

y´ = y + y´

= j – d*e +     i *e mod t

= j - (dp +      i) e +       i*e mod t y´ = j - dp* e mod t

Proxy multi-signature verification: When the verifier verifies the signature, he or she use proxy public value Qp corresponding to the proxy signature key dp. Then the verifier can confirm the validity of Sigd (m) by validating the verification equality of the designated signature scheme.

Step 1 : Compute J̅ = y × B + e × Q P = (J̅ x ,J̅ y )

Step 2 : And compute e´ = h (J̅ x ,m) . Then check that e´ = e and if these are equal then valid signature otherwise not.

• C.    Framing Attack

On behalf of users A1, A2… An, malicious users A1, A2… An can forge a proxy multi-signature for message m by some user P, such that user P was never designated by users A1,A2…An. Suppose proxy signer P signed a message with his private key dp, the signature is (m, mw, R, e, y´) where e= h(m, jx) and y´´= j-dp *e (mod t).

Upon received the signature (m, mw, R, e, y´´), the malicious original signers A1…An can forge proxy multi-signature by performing following steps:

• •    The malicious users A 1 ,A 2 …A n pretend to produce a forge warrant m w , which recording the delegation information such as identities of the malicious users A 1 ,A 2 …A n and user P .

• •    For each 1≤ i ≤n, the malicious user A_i selects a random number 1≤ k_i ≤ t– 1, and then computes R_i = k_i X B = (x_Ri^, y_Ri) and broadcast R_i to other users.

• •    On receiving R j (1 ≤ j ≤ n, j ≠ i), A_i calculates

R= ∑ⁿ R i =(x R ^, y R )                           (14)

s i = d i * h(M w , x Q _p, x Q _i x R ) – k i * x R (mod t)      (15)

Note that user P doesn’t receive any information from the malicious users A1, A2…An.

• •    Compute y´=    i 5_i *e mod t;

• •    Compute y= y´´- y´

Finally the malicious users can forge a valid signature (m, mw, R, e, y) on message m by some user P on behalf of users A1…An, such that user P was never designated by users A1…An. The following shows why the signature (m, mw, R, e, y) is valid.

PROFF:

y = y´´- y´

= j-dp * e mod t -si *e mod t

= j-(dp +2^=isi) e mod t y = j- d*e mod t

From above we can see that the malicious users A1…An framed innocent user P.

Proxy multi-signature verification phase: When the verifier verifies the signature, he or she calculates the proxy public value Q corresponding to the proxy signature key d as

Step 1 : (Secret key generation): For each 1≤ i ≤n, the original signer A_i selects a random number k_i {1, 2… t– 1}/ d_i as secret key.

Step 2: (Group commitment value generation): Then computes Ri = ki × B = (xRi ,yRi). If xRi =0 then return to step 1; otherwise Ai broadcasts Ri to other original signers. On receiving Rj (1 ≤ j ≤ n, j ≠ i), Ai calculates i = (xR,yR)                         (17)

Step 3 : (Sub-delegation parameter generation): For each 1≤ i ≤n, the original signer A_i uses his own secret keys d_i, k_i and the group commitment value x_R to compute the following.

s i = d i * h(M w , x Qp ,x Qi , x R ) – k i * x R (mod t)

Where h ( ) is a public collision-resistant hash function and the warrant M_w contains information such as the IDs of all original signers and proxy signer, and the delegation period. Then, the sub-delegation parameter for A i is (M w ,s i ).

Step 4 : (Sub-delegation parameter delivery): For each 1≤ i ≤n, the original signer A_i sends (M_w, s_i) to the proxy signer via a public channel.

Step 5: (Sub-delegation parameter verification): After the proxy signer has received the subdelegation parameters then the proxy signer P computes si *B= h(Mw, xQp,xQi, xR) *Qi – xR * Ri     (19)

Checks whether it holds. If it holds then theproxy signer accepts (M_w,s_i) as a valid subdelegation parameter; otherwise, he can reject it and requests a valid one A i , or terminate this protocol.

Step 6 : (Proxy multi-signature secret key generation): Then computes the proxy multi-signature secret key as follows:

d = x Q _{p *} d p +      i mod t               (20)

Phase 3: Proxy multi-signature generation phase: The proxy multi-signature affixed to the m is in the form of (m,mw,R,Sigd(m)), where Sigd(m) is the signature generated by a designated signature scheme (EC-schnorr signature scheme) using the proxy signing key d and m is message.

Step 1 : Proxy signer P choose random number j where 1≤ j ≤ t– 1 and calculate J = j × B = (J_x,J_y).

Step 2 : Compute e= h(m, J_x) where h(J_x, m) is hash function. If e = 0 then go to step 1.

Step 3: Compute y = j - d × e (mod t)                        (21)

and the output sign d (m) = (e,y).

Phase 4: Proxy multi-signature verification phase: When the verifier verifies the signature, he or she calculates the proxy public value Q corresponding to the proxy signature key d as

Q= x Q _p * Q P +       (M w , x Qp , x Qi , x R ) × Q i – R * x R

With the value, the verifier can confirm the validity of Sig d (m) by validating the verification equality of the designated signature scheme.

Step 1 : Compute J̅ = y × B + e × Q = (J̅_x,J̅_y)

Step 2 : And compute e´ = h (J̅_x,m) . Then check that e´ = e and if these are equal then valid signature otherwise not.

• V. CONCLUSIONS

In this paper, we have reviewed improved CCH1 and improved CCH2 proxy multi-signature scheme based on elliptic curve cryptosystem. We have shown time complexity, space complexity and computational overhead of improved CCH1 and CCH2 proxy multisignature schemes. We have presented cryptanalysis of improved CCH2 proxy multi-signature scheme and showed that improved CCH2 scheme is suffered from various attacks i.e. the malicious original signers can forge the proxy signer’s signature, forge a proxy signature and frame anyone who was never designated as proxy signer. In addition, we have proposed an enhanced proxy multi-signature scheme based on ECC. Enhanced scheme does not suffer from these given attacks.