Сегментация изображений кластерным методом и алгоритмом случайных скачков: сравнительный анализ

Одним из часто применяемых в приложениях методов сегментации изображений является кластерный анализ (смотри, например, [1, 2]), причисляемый иногда к пороговой сегментации [3]. Обработка изображения при использовании данного метода заключается в разделении всех элементов изображения (ЭИ) на группы (кластеры) элементов, в чем-то схожих между собой (по яркости, текстуре и т.п.). Процедура кластеризации основывается на оптимизации какого-нибудь показателя качества, например, на критерии минимума суммы квадратов ошибки:

K

£ = HI к k - ckl Г, (1) k=1 xe Sk где xk – вектор значений признаков, K – число кластеров, Sk – множество объектов (элементов изображения), относящихся к k-му кластеру, сk – вектор средних значений для класса k. Процесс обработки изображения в данном случае представляет собой итерационное нахождение центров кластеров и разбиение изображения на кластеры до тех пор, пока величина £ не перестанет уменьшаться.

Существует множество алгоритмов, реализующих задачу кластеризации: алгоритм быстрого выделения кластеров, итерационный алгоритм последовательной кластеризации и т.д. [4]. В зависимости от используемого алгоритма необходимо задание различных априорных данных, например, итерационный алгоритм последовательной кластеризации требует задания числа кластеров и значений их центров.

Сегментация изображений эффективно выполняется алгоритмами на основе модели системы со случайной скачкообразной структурой (ССС), описанными в [5,6]. Система в i -й структуре, а в рассматриваемом случае – изображение в i -м классе, описывается уравнением:

X k +1 = ф к ) X k + С к ⁽ ' ) , (2)

где λ _k – вектор значений признаков, Φ ⁽ _k ^{i )} – известная матрица, { с _k ⁽ ‘) } - последовательность статистически независимых случайных величин с известными плотностями вероятности, ( i = 1, M , k = 0,1,...). Процесс смены классов описывается дискретной марковской последовательностью { 0 _k } , состояния которой являются номерами классов i . Случайные величины { X _k , 0 _k } образуют смешанную марковскую последовательность с известными начальными и переходными плотностями вероятности. Задача состоит в оценивании номера i по наблюдениям { X _k } .

При решении поставленной задачи априорные данные помимо числа выделяемых на изображении классов и средних для каждого класса включают сведения о коррелированности ЭИ и вероятностях перехода элементов из одного класса в другой. Использование этой дополнительной степени свободы для «подстройки» работы алгоритма с определенным классом изображений дает основание предположить, что сегментация изображения алгоритмами на основе модели ССС будет более эффективной.

Целью настоящей работы является сравнение эффективности сегментации изображений алгоритмами на основе модели системы ССС и кластерного анализа путем имитационного моделирования.

1.    Результаты имитационного моделирования сегментации изображений

Исследование проводилось для двух классов изображений: первый класс был представлен однородным фоном, второй класс – совокупностью кругов разного диаметра. Кромки кругов формировались изрезанными для облегчения визуализации результатов сегментации. Статистические характеристики изображений выбирались различными. В первом случае элементы изображения были коррелированными и формировались в соответствии с моделью разделимого случайного поля с гауссовским распределением. Во втором случае независимые ЭИ формировались в соответствии с гамма- распределением, выбор которого был обусловлен его широким использованием в приложениях. На рис. 1 а, б приведены - исходное незашумленное изображение и пример зашумленного изображения для первого случая. Обработка изображений осуществлялась различными алгоритмами сегментации на основе модели системы ССС: однострочными ОА1, ОА2, комбинированными однострочными КОА1, КОА2 и итерационным алгоритмом последовательной кластеризации КЛ [4].

а)

р x,y ^(1,2) =0,1; дисперсия о\ случайной величины, описывающей яркость на изображении, равнялась двум.

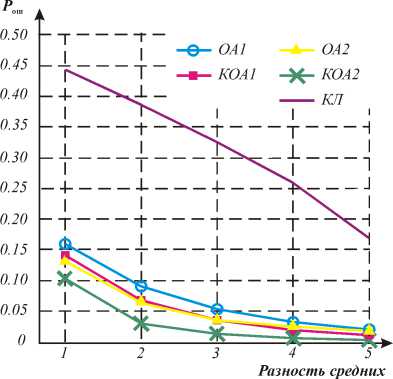
Рис. 2. Зависимость ошибки распознавания состояния от разности средних для исходных изображений с гауссовским распределением

На рис. 3 а - в показаны исходное изображение и результаты его обработки алгоритмами КОА2 и КЛ при разности средних, равной пяти. Из рисунков видно, что ошибка распознавания для алгоритмов сегментации на основе модели системы ССС много меньше по сравнению с алгоритмом КЛ за счет безошибочной передачи внутренних областей изображений одного класса. Границы между изображениями разных классов передаются алгоритмами сегментации на основе модели системы ССС достаточно отчетливо, несколько сглаживаясь при обработке.

• б)

Рис. 1. Исходное незашумленное изображение (а) и пример зашумленного изображения с гауссовским распределением (б)

Ошибка в определении номера класса оценивалась величиной Р _ош, называемой ошибкой распознавания состояния:

LK

рош = T^XZ zi, k, LK l=1 k=1

где L,K - размеры изображения по вертикали и горизонтали , zi k - величина, принимающая значение нуль в случае, когда оценка номера класса 9 l,_k и номер класса 9 l,_k l,k -го ЭИ незашумленного изображения совпадают, и равная единице в противном случае. Усреднение результатов проводилось по 500 реализациям.

На рис. 2 представлены графики зависимости Р ош от разности средних для модели гауссовского разделимого случайного поля. Параметры моделей определялись следующим образом: коэффициенты корреляции по строке и столбцу изображений обоих классов принимались равными в обозначениях [5,6]

а)

б)

Рис. 3. Исходное изображение с гауссовским распределением (а), результаты его сегментации алгоритмом КОА2 (б) и алгоритмом КЛ (в)

На рис. 4 а , б представлены графики зависимости Р _ош от разности средних для изображений с независимыми элементами и гамма-распределением при двух значениях параметра формы N , равных четы-

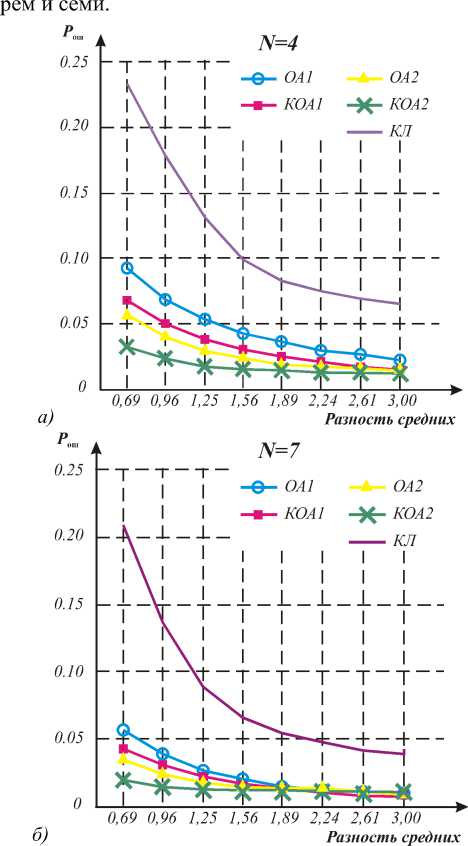
Рис. 4. Зависимость ошибки распознавания состояния от разности средних для исходных изображений с гамма-распределением при N=4(а) и N=7(б)

Необходимо отметить, что алгоритмы сегментации на основе модели системы ССС предназначены для обработки массивов с коррелированными элементами. Поэтому независимость соседних ЭИ для упомянутых алгоритмов является фактором, затрудняющим их работу. Тем не менее, данное обстоятельство было учтено: при обработке исходных изображений предполагалась слабая корреляционная связь между ЭИ – значения коэффициентов корреляции по строке и столбцу изображений были приняты малыми ρx,y(1,2) =0,1.

На рис. 5 а-в показаны исходное изображение и результаты его обработки алгоритмами КОА2 и КЛ при разности средних, равной 1,89, и N =4.

Рис. 5. Исходное изображение с гамма-распределением (а), результаты его сегментации алгоритмом КОА2 (б) и алгоритмом КЛ (в)

Из рисунков видно, что алгоритмы сегментации на основе модели системы ССС показывают высокую эффективность, несмотря на независимость элементов исходного изображения. Ошибка распозна- вания для них, аналогично предыдущему случаю, много меньше по сравнению с алгоритмом КЛ. Внутренние области изображений одного класса передаются без искажений в отличие от обработки алгоритмом КЛ. При увеличении значения параметра N ошибка распознавания уменьшается. Границы между изображениями разных классов передаются с искажениями как алгоритмами сегментации на основе модели системы ССС, так и алгоритмом КЛ.

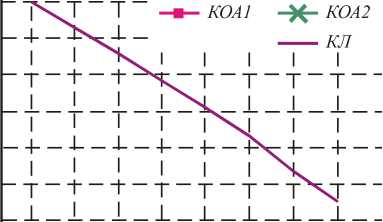
Известно, что при логарифмировании случайной величины с гамма-распределением закон ее распределения становится близким к гауссовскому [7]. Это соответствует условиям применения алгоритмов сегментации на основе модели системы ССС. По- этому были проведены исследования алгоритмов после выполнения операции логарифмирования ЭИ. Графики, аналогичные вышеприведенным, но с учетом выполнения операции логарифмирования, приведены на рис. 6а, б.

ош

0.50

0.45

0.40

0.35

0.30

0.25

0.20

0.15

0.10

0.05

N=4log

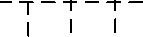
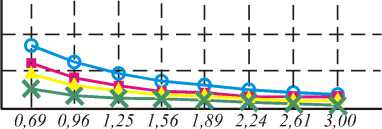
Разность средних

ош

0.50

0.45

0.40

0.35

0.30

0.25

0.20

0.15

0.10

0.05

0 б)

N=7log

ОА2

КОА1

КЛ

I _ I _ I _ I

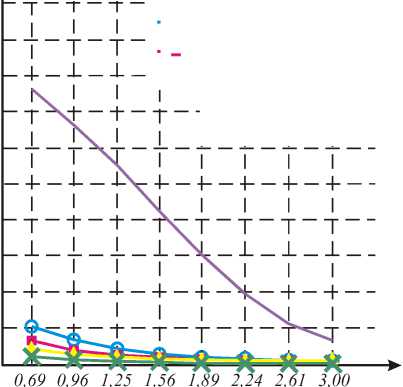
Разность средних

Рис. 6. Зависимость ошибки распознавания состояния от разности средних для исходных изображений с гамма-распределением после логарифмирования при N=4(а) и N=7(б)

На рис. 7 показаны результаты обработки исходного изображения (рис. 5 а ) алгоритмами КОА2 и КЛ.

Из рис. 6 и 7 видно, что выполнение операции логарифмирования перед обработкой приводит к увеличению ошибки распознавания состояния для алгоритма КЛ и ее уменьшению для алгоритма КОА2. Этот вывод подтверждают результаты сегментации реального изображения.

Рис. 7. Результаты сегментации исходного изображения с гамма-распределением после его логарифмирования алгоритмом КОА2 (а) и алгоритмом КЛ (б)

Для визуального сравнения выполнения операции сегментации рассмотренными алгоритмами ниже приведен пример обработки реального изображения участка местности, полученного когерентным локатором (рис. 8а). Участок местности представлен двумя классами, описание которых близко к гамма-распределению со следующими параметрами: средние m(1) = 76, m(2) = 129; среднеквадратические отклонения o(1) = 8; o(2) = 16. На рис. 8б приведен результат обработки изображения алгоритмом КОА2 при выполнении предварительного логарифмирования, а на рис. 8в – алгоритмом КЛ без предварительного логарифмирования.

б)

в)

Рис. 8. Результаты сегментации реального изображения (а) после логарифмирования алгоритмом КОА2 (б) и без логарифмирования алгоритмом КЛ (в)

Заключение

В работе приведены результаты сравнения эффективности сегментации изображений алгоритмами на основе модели ССС и кластерного анализа путем имитационного моделирования изображений с коррелированными и независимыми элементами.

Учет при обработке изображений алгоритмами на основе модели системы ССС дополнительных данных о степени коррелированности элементов изображения и вероятностях перехода элементов из одного класса в другой обуславливает в общем случае их более высокую эффективность по сравнению с алгоритмом КЛ. Исследования показали, что при сегментации изображений алгоритмами на основе модели системы ССС внутренние области изображений одного класса обрабатываются со значительно меньшим количеством ошибок по сравнению с алгоритмом КЛ, в то же время границы между изображениями разных классов сглаживаются, хотя выделяются достаточно отчетливо. Полученные характеристики эффективности алгоритмов могут быть использованы при обосновании их применения в приложениях.