Сегментация изображений органов забрюшинного пространства по компьютерным томографическим изображениям на основе функции уровня

Технологии 3D-моделирования данных компьютерной томографии (КТ) всё активнее применяются врачами в медицинской практике, значительно повышая информативность исследований [1 –4], облегчая определение патологий или оптимизируя этап предоперационного планирования [5, 6]. Однако для некоторых клинических задач, подобных хирургическому предоперационному планированию [5, 6, 9, 10], необходимо понимать трёхмерную структуру данных, что является довольно сложной задачей и во многом зависит от опыта самого врача. Сегментация изображения является необходимым этапом обработки изображений для решения подобных задач [5, 7, 8]. Сегментированная 3D-визуализация органов человека с координатной привязкой к пациенту значительно облегчает понимание изображения и ускоряет процесс обучения для начинающих хирургов. 3D-представление сегментированных моделей органов человека является неотъемлемой частью всех хирургических симуляторов [7, 11 – 13], которые имитируют хирургические действия на виртуальных моделях.

В работе рассматривается применение функции уровня для численного моделирования процесса сегментации изображений органов пациента по результатам томографического обследования. Процесс сегментации зависит от многих факторов, таких как искривление сегментированных областей, распределение интенсивностей или структура изображения. Для методов на базе функции уровня характерна приспосабливаемость к параметрам исходного изображения, что позволяет уменьшить сложность управления процессом сегментации медицинских изображений.

Цель работы : разработка алгоритма сегментации изображений органов человека по КТ-изображениям на основе функции уровня.

1.    Теоретический анализ

Применительно к томографии под задачей сегментации изображения понимается задача разделения цифрового изображения на множество непересекаю-щихся областей или наборов пикселей, имеющих одинаковую признаковую характеристику, например, текстуру, интенсивность или цвет, в зависимости от типа ткани и анатомической структуры. Смежные области отличаются друг от друга этими же характеристиками. Результатом сегментации является набор областей, покрывающих вместе всё изображение, и набор контуров, извлечённых из них.

К настоящему времени задача сегментации в общем случае считается нерешённой, поскольку не существует чёткой и однозначной общей постановки задачи. Результат работы методов, основанных на машинном обучении [14, 15], довольно сильно зависит от характеристик обучающего множества. Методы, основанные на априорных моделях [16, 17] и вероятностных атласах [18, 19], также обладают рядом проблем, поскольку требуют трудоёмких операций на предварительной стадии формирования моделей: коллекционирование и классификация выборок и ручная сегментация. Эти методы в большинстве случаев высокоэффективны и просты, но в то же время выдают неадекватные результаты при обработке нестандартных изображений или обладают высокой вычислительной стоимостью. Методы на основе активных контуров и функций уровня более универсальны и лишены подобных проблем. Lefohn и др. [20] и Cates и др. [21] показали, что методы сегментации на основе функции уровня уменьшают сложность процесса сегментации медицинских изображений. Основную сложность при их разработке составляет синтез адекватной функции скорости и её параметров.

Пусть исходное изображение представлено в виде 4-мерной скалярной (x, y, z, i) области, где x, y, z – ко- ординаты пикселей, а i – значение интенсивности. Тогда под функцией уровня ϕ(u) : ℜ4 → ℜ , u = (x, y, z) изображения понимается математический объект ϕ , неявно представляющий сегмент изображения и делящий изображение на внутреннюю Ω1 и внешнюю Ω2 области (рис. 1). Область Ω1 соответствует выделяемому сегменту, а область Ω2 – другим сегментам или фону. Функция ϕ(u) задаётся скалярным полем, принимающим положительные значения для региона Ω1 и отрицательные для Ω2 :

Ω ₁ = { u : ϕ ( u ) ≥ 0} и Ω ₂ = { u : ϕ ( u ) <  0} , (1) где u = ( x , y , z ) – координата пиксела изображения.

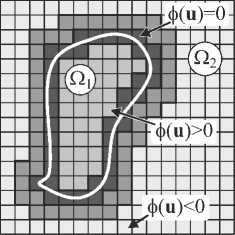
Рис. 1. К определению функции уровня

В случае, если число сегментируемых регионов N > 2, то используется N функций уровня { ϕ _h } _h ^N _{= 1} , разбивающих изображение на регионы { Ω _h } _h ^N _{= 1} . Контура B_h сегментов определяются точками, лежащими на границе регионов { Ω _h } _h ^N _{= 1} , т.е.

B h = { u : ϕ h ( u ) = 0}. (2)

Функция уровня ϕ _h инициируется 3D-областью V_h ⁰ (также называемой затравочной областью или «зерном») в пределах 3D-изображения:

ϕ _h ( u ) = 1, ∀ u : u ∈ V_h ⁰ , ϕ _h ( u ) =- 1, ∀ u : u ∉ V_h ⁰. (3)

Поверхность функции ϕ итеративно искажается таким образом, чтобы выделить интересующий регион изображения. При этом движение функции ϕ происходит вдоль нормали N = - ( ∇ ϕ ( u ) I | ∇ ϕ ( u ) |) к поверхности функции ϕ в точке u . Скорость эволюционного процесса функции ϕ регулируется локально зависимой функцией скорости F ( u , t ):

ϕ ( u , t +∆ t ) = ϕ ( u , t ) +∆ t ⋅ F ( u , t ) ⋅ ∇ ϕ ( u , t ) , (4)

где u – координата пиксела, t – текущее время процесса сегментации, ∆ t – дискретизация по времени, ϕ ( u , t ) и ϕ ( u , t +∆ t ) – значения функции уровня на последней и следующей итерациях. С более полным обзором методов на основе функции уровня и их применением к сегментации изображений можно ознакомиться в работах Sethain [22], Osher и Paragios [23].

2.    Математическая модель изображения

В работе использовались данные стандартного клинического обследования спиральной компьютерной томографии, выполняемого на аппаратах Philips Brilliance 64 и Siemens Somatom 40, при сотрудничестве с Республиканской клинической больницей РМЭ. Изображения сохранены в формате DICOM.

КТ-изображение I представляет собой упорядоченный набор I = { I_z } _z ^N ₌ ^- ₀¹ из N рентгеновских снимков тела человека, сделанных с определённым расстоянием K = { k x , k y , k z } между пикселами. Каждый пиксел u = ( x, y, z ) такого изображения кодируется смещённой величиной количественной оценки плотности I ( u ) структур тканей человека по шкале Хаунс-филда. Диапазон единиц шкалы составляет от -1024 до +3071, значение интенсивности пиксела лежит в диапазоне 0 ≤ I ( u ) ≤ 4095. Диапазон достаточно широк и позволяет уверенно классифицировать отдельные ткани [8].

Изображения органов забрюшинного пространства на КТ-снимках, получаемых в результате обследования, имеют непостоянную интенсивность. Это вызвано неоднородностью структуры тканей и органов, большая часть тканей содержит в себе кровь, что приводит к «зашумлению» изображений. Элемент случайности также заложен в самой природе источника излучения. Таким образом, математическая модель КТ-изображения I имеет следующий вид:

I = b ⋅ J +Ζ , (5) где J – неискажённое («идеальное») изображение, b – компонента, связанная с неоднородностью изображения, Z – аддитивный шум, I – результирующее изображение, выдаваемое томографом. Будем считать, что в пределах одной ткани компонента b изменяется монотонно и плавно, а компонента шума Z – подчиняется нормальному закону распределения.

3.    Предварительная обработка изображения

В разделе рассматривается метод предварительной обработки изображений, снижающий влияние шумовых компонент b и Z (5) и приближающий результат обработки к «идеальному» изображению J , при сохранении границ между областями-сегментами.

Традиционные способы удаления шума, улучшения краёв и реконструкции размытых изображений опираются на методы высокочастотной фильтрации или обратного распространения уравнения диффузии во времени. Задачу в текущей постановке можно решить, используя в качестве физической основы нелинейный процесс диффузии. P. Perona и J. Malik [24] описали, что если коэффициент проводимости выбран в соответствии с функцией градиента изображения, то диффузия будет одновременно сглаживать изображение и усиливать края, стабилизируя изображение к ступенчатому виду. Результат гарантируется принципом максимума уравнения диффузии.

Фильтр анизотропной диффузии работает следующим образом. На вход фильтра подаются изобра- жения I срезов томограмм, масштабные коэффициенты K = {kx, ky, kz} КТ-изображения, описывающие физические расстояния между пикселями и учитываемые при вычислении градиента VI(u). Далее ите- ративно каждому пикселю присваивается новое значение интенсивности согласно формуле:

I '( u ) = I ( u ) + A I ( u ) =

= I ( u ) + v- div ( V I ( u ) • exp ( - ( V I ( u )| / к ²) ) ) .

Если диффузия A I ( u ) в некоторой фиксированной окрестности точки u велика, то эта интенсивность в этой точке является шумом и значение интенсивности корректируется в сторону доминирующей интенсивности. Если диффузия A I ( u ) мала, то точка принадлежит границе и размытие не происходит. С более детальным описанием механизма работы фильтра можно ознакомиться в статье P. Perona и J. Malik [24]. Среди достоинств фильтра стоит отметить стабильность и распараллеливаемость.

Градиент V I ( u ) оценивается для 3x3x3 окрестности точки. Число шагов итераций равно 16 [24]. Выбор параметра v , отвечающего за плавность процесса диффузии, рассмотрен в статье G. Gerig и др. [25]. В настоящей работе используется значение v = 0,142857. Параметр к играет ту же роль, что и среднеквадратическое отклонение в модели нормального закона распределения, и влияет на процесс сглаживания. Чем больше значение параметра к , тем больший диапазон интенсивностей подвергается сглаживанию. Экспериментально установлен рабочий диапазон значений параметра к для КТ-изображений органов забрюшинного пространства: к ~ 25 ± 5.

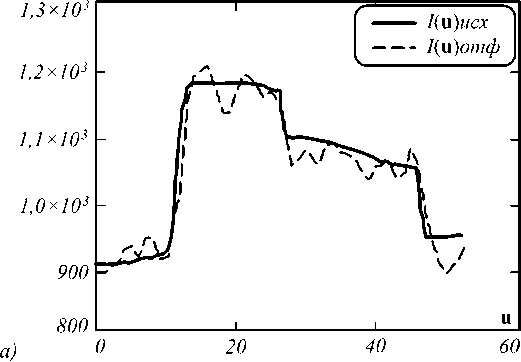
На рис. 2 показан результат работы фильтра анизотропной диффузии.

4.    Детекторная функция границ

Поскольку на предыдущем шаге используется фильтр анизотропной диффузии, который минимизирует разброс значений в однородной области, но сохраняет границы, то в роли детекторной функции границ можно использовать функцию вида:

g ( u ) = V(1 + 0 2 [ I ( u ) ] ), (7)

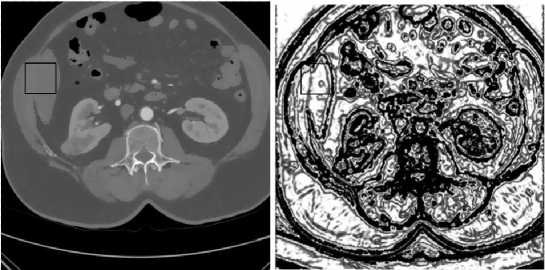
где о ² [ I ( u ) ] – дисперсия значений яркостей в области радиуса r = 1,5 пикселей вокруг точки u . Данный вид функции обнаруживает границы с достаточной чувствительностью к слабым перепадам яркости. На рис. 3 б показан результат работы функции детектора границ (7). Стоит обратить внимание на фрагмент КТ-изображения, содержащий переход от печени к мышцам (рис. 3 a , выделен квадратом). Как видно из рис. 3 б , детектор обнаруживает эту границу.

5.    Функционал функции уровня

Для управления эволюцией функции уровня (4) используется локально зависимая функция скорости F ( u , t ).

б)

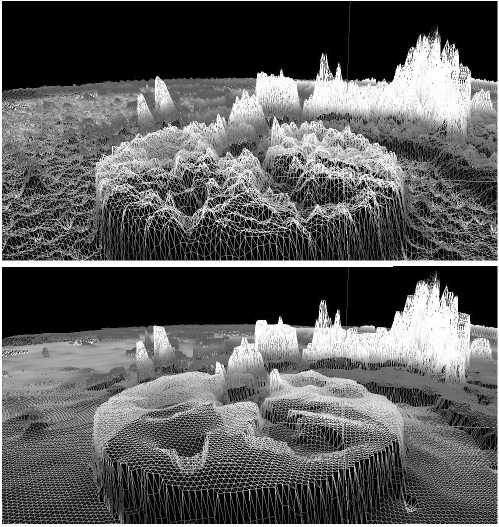
Рис. 2. Работа фильтра анизотропной диффузии: а) для одномерного среза (сплошной линией обозначено исходное изображение, пунктиром – отфильтрованное); б) для одного 2D-среза, интенсивность отложена по оси 0Z, верхний рисунок – исходный фрагмент изображения, нижний – изображение после фильтрации

а)                                 б)

Рис. 3. Результат работы функции детектора границ g(u): а) КТ-изображение после применения фильтра анизотропной диффузии; б) отображение значений функции g(u), белые области соответствуют однородным участкам изображения, чёрные области – граничные области между сегментами

Функция оценивает скорость эволюции согласно локальному поверхностному искривлению функции уровня ф(u, t) и локальной интенсивности изображения I. К функции скорости предъявляются два требо- вания. Во-первых, функция ф(и, t) должна изменяться вдоль нормали к её поверхности. Во-вторых, эволюция функции ф(и, t) должна тормозиться при достижении границ сегмента.

Функция скорости для функции уровня ф _h строится по схеме со сглаживанием [26]:

F h ( u , t ) = а- C h ( и , t ) + (1 -а ) • D h ( и ), (8) где ае [ 0,1 ] является сглаживающей функцией, которая контролирует относительное влияние значений кривизны C h ( u , t ) и информационного терма D h ( и ) на поведение функции скорости, h - номер функции уровня. Значение параметра а можно связать с функцией детектора границ: а = g ( и ) (7). Этот приём позволяет схеме плавно переключаться между режимами распространения вдоль нормали к функции для однородной области ( g ( и )>0) и распространения вблизи границы между сегментами ( g ( и ) = 0).

Информационный терм D_h ( и ) отвечает за знак и силу функции скорости для h- й функции уровня и определяется следующим образом:

D h ( и ) = 8 h -| I ( и ) - T h\ , (9) где I ( и ) - функция интенсивности изображения, T h -целевая интенсивность, стимулирующая максимальный рост поверхности, а £ _h - диапазон интенсивности, в рамках которой функция уровня должна расти. Если значение интенсивности I ( и ) в точке и удовлетворяет условию T h - £ _h < I ( и ) < T h + £ _h , то D_h ( и ) способствует росту (расширению) области, иначе - сжатию области.

Распределение интенсивностей биологической ткани носит случайный характер. Экспериментальная проверка на группе пациентов показала, что распределение интенсивностей отдельных структурных элементов органов и тканей в пределах изображения одного пациента соответствует нормальному закону распределения с доверительной вероятностью 0,95 (тест Колмогорова). Следовательно, количественные оценки параметров T h и £ _h можно задать математическим ожиданием ц _h и среднеквадратическим отклонением о _h для каждой функции уровня:

T h = Ц h = M [ I ( и ) ] ,

8 _h = к •о _h = k ^о [ I ( и ) ] , и еф ^h , (10) где k - параметр, выбираемый, например, по правилу «трёх сигм», к = 3.

Параметры T h и £ _h итеративно изменяются в процессе эволюции каждой функции уровня. Начальные значения параметров оцениваются по значениям интенсивности инициирующего набора точек затравочной области V .

Кривизна функции уровня в точке и определяется как локальная дивергенция нормированного градиента функции уровня на предыдущей итерации:

C_h ( и , t ) = div

Уф _h ( u . t -A t ) | ^у ф h ^{( u} .^{t -A} t )|

Градиент У рассчитывается для области 3^Х3^Х3 пикселей по схеме, приведённой в [26]. Такая область связности даёт более гладкую оценку кривизны поверхности функции уровня.

В роли исходных затравочных областей V_h ⁰ используются 3D сферические фрагменты изображения радиуса р = 3 пикселя с центрами в точках и _А , расположенных в узлах регулярной сетки.

Т.к. точки, попадающие в окно сферы, используются для оценки начальных статистик T h и £ h , то для их корректной оценки центры и 0 должны лежать внутри сегментируемой области и не должны оказаться на границе двух сегментов. Если затравочная область лежит на границе сегментов, то распределение интенсивностей характеризуется высоким уровнем дисперсии из-за наличия нескольких центров масс. Следовательно, критерием отсева таких областей может служить условие для среднеквадратического отклонения с порогом, например, £ _h >  20.

В процессе эволюции неизбежна ситуация, когда две функции уровня будут соприкасаться своими границами. В этом случае оцениваются количественные значения степени сходства значения интенсивности пиксела и для каждого из конкурирующих сегментов Q _h с помощью функции правдоподобия:

. _        1 Г (I(и) — ц,) ^__

Lh (и) =----exp I -1 1 ’ 2      I о h V2n (     2o h и по критерию максимального правдоподобия пиксел будет относиться к одному из смежных сегментов.

На каждом шаге процесса сегментации ведётся статистика эволюций функций уровня в виде счетчика Count добавляемых/исключаемых точек.

n          [ ⁰,

Count = и е I L ¹,

ф ( и , t ) = ф ( и , t + A t ) ф ( и , t ) ^ ф ( и , t + A t )

Процесс эволюции продолжается до тех пор, пока функции уровня не стабилизируются, их рост прекратится, а счётчик Count не станет меньше некоторой пороговой величины Count_nopor .

На последнем этапе происходит слияние смежных функций уровня, обладающих общей статистикой, например, по критерию Колмогорова-Смирнова [27].

Таким образом, предлагаемый обобщённый алгоритм сегментации изображений на основе функции уровня имеет следующий вид:

• 1.    Применение фильтра анизотропной диффузии для каждой точки ие I согласно уравнению (6).

• 2.    Расчёт функции детектора границ g(и) для окрестности радиуса r =1,5 пикселей каждой точки и согласно уравнению (7).

• 3.    Генерация множества затравочных областей {V_h°}N=i и инициализация функций уровня {ф_h}N₌₁ согласно выражениям (3) и (10).

• 4.    Итеративное изменение функции уровня согласно уравнениям (4) и (8) до стабилизации.

• 5.    Визуализация результата.

6.    Результаты и дальнейшая работа

Данный алгоритм реализуется по схеме с параллельными вычислениями. При этом на этапах 1 и 2 нет необходимости в синхронизации взаимодействия одновременно выполняемых потоков. В то время как этапы 3 и 4 в процессе работы требуют реализации механизма синхронизации и контроля взаимоисключающего доступа к общим ресурсам.

Алгоритм был реализован в составе программного продукта «Volga-M», разрабатываемого на кафедре радиотехнических и медико-биологических систем при сотрудничестве с урологическим отделением Республиканской клинической больницы РМЭ. Работа была проверена на КТ данных трёх пациентов с патологиями урологического характера. Результат работы алгоритма с одним зерном на одном из изображений с почкой и опухолью показан на рис. 4.

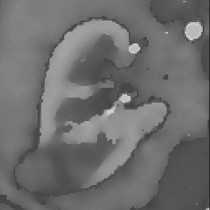
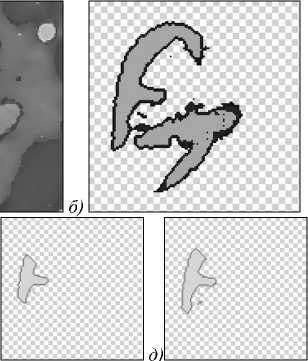
б)

Рис.4. Пошаговая эволюция функции уровня для одного зерна: а) исходное изображение почки, б) результат сегментации коркового вещества почки, в) – ж) вид функции уровня на 10, 20, 30, 50 и 70 итерации соответственно

В целом алгоритм работает стабильно и позволяет сегментировать отдельные классы и структуры органов пациента. При работе в режиме сегментирования множества зёрен формируется сегментированное изображение органа пациента. На рис. 5 показан процесс эволюции функций уровня в этом режиме сегментирования изображения. Экспертная оценка в лице практикующего врача показала, что основные структуры почки выделяются корректно.

К недостатку текущей реализации алгоритма можно отнести недостаточно эффективное использование результатов, получаемых на этапе выделения границ.

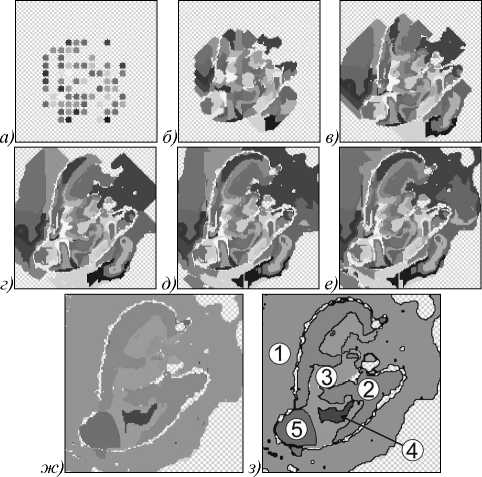
Рис.5. Пошаговая эволюция функции уровня для множества зёрен: а) вид исходного множества зерен, б) –е) вид функций уровня на 10, 30, 50, 70, 90 итерациях соответственно, ж) – з) результат сегментации на 90 итерации после объединения смежных функций уровня: окружающей ткани (1), коркового вещества почки (2), паренхимы почки (3, 4), опухоли (5)

Потенциально сочетание фильтра анизотропной диффузии и функции детектора границ обнаруживает границы между сегментами с плавно изменяющимися яркостными характеристиками. Реализация схемы эволюции функции уровня совместно с методами морфологической обработки результата детекторной функции границ может позволить сформировать более строгие эволюционные условия. Данному направлению будет посвящена дальнейшая работа над проектом.

Заключение

В работе предложен метод сегментации органов забрюшинного пространства на томографических изображениях на основе функции уровня. Для реализации данного метода рассмотрена математическая модель КТ-изображения, учитывающая статистические свойства структурных элементов органов и тканей и влияние помех. На основе построенной математической модели предложен метод предварительной обработки изображения, основанный на применении нелинейного адаптивного фильтра анизотропной диффузии, сглаживающего изображение при сохранении границ между сегментами, и функции детектора границ на базе оценки дисперсии значений окрестности точки. Такой подход к предварительной обработке изображения позволяет избавиться от влияния шумовой компоненты, сохранить информацию о внутренней структуре тканей и органов за счёт сохранения границ между крупными изолированными сегментами. Синтезирован алгоритм сегментации томографического изображения на основе функции уровня и активных контуров и приведены примеры его работы. Разработанный алгоритм может использоваться в инженерной и медицинской практике при раз- работке программ обработки медицинских изображений, обучающих программ-симуляторов предоперационного планирования и интраоперационной навигации.

Работа выполнена в рамках программы УМНИК-2014, проводимой Федеральным государственным бюджетным учреждением «Фонд содействия развитию малых форм предприятий в научно-технической сфере» (государственный контракт № 4334ГУ1/2014, код 000790))