Сегментация когерентно-локационных изображений со статистически независимыми элементами

Как известно, изображение подстилающей поверхности, сформированное когерентным локатором, характеризуется слабой статистической связью между соседними элементами изображения (ЭИ) вследствие присутствия на нем шума пятнистости, называемого также спекл-шумом. По этой причине при описании когерентно-локационных изображений зачастую применяют модели с независимыми соседними элементами. Плотность вероятности случайной величины y, описывающей распределение яркости изображения однородного участка (ОУ) подстилающей поверхности, отличается от гауссовского и для локатора с некогерентным накоплением представляется гамма-распределением [1]:

Р ( У ) = y N ^- 1 в^{- N} exp( - y / в )/Г( N ), (1)

где в =s/ N , s - значение средней удельной эффективной поверхности рассеяния (СУЭПР) при работе локатора в радиодиапазоне, N - число некогерентных накоплений изображений одного и того же участка местности, Г( N ) - гамма-функция.

Спекл-шум имеет существенно мультипликативные свойства, и поэтому зависит от структуры самого изображения и, в частности, от вида подстилающей поверхности. Можно было ожидать, что предварительная фильтрация (со сглаживанием) изображения не приведет к полному исчезновению данных о связности и других параметров отдельных элементов фона – подстилающей поверхности. Кроме этого, следует учесть, что распределение (1) относится к совокупной системе «изображение+шум», тогда как реальное изображение характеризуется нормальным распределением яркостей, что характерно и для некогерентных изображений.

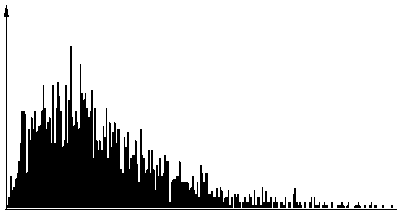
Для сглаживания спекл-шума широко применяют различные методы пространственной фильтрации изображения [2]. Среди них высокой вычислительной эффективностью обладают локальные методы, позволяющие формировать оценки поля не-зашумленного изображения путем анализа и обработки ограниченных и достаточно малых по размерам фрагментов. Примечательно, что после обра- ботки изображений локальными фильтрами плотность вероятности случайной величины y становится близкой к гауссовской [3], а соседние ЭИ становятся коррелированными. В качестве иллюстрации на рис. 1 приведены гистограмма значений синтезированного изображения с распределением (1) и одномерная функция корреляции изображения до и после обработки фильтром Lee [4].

а)

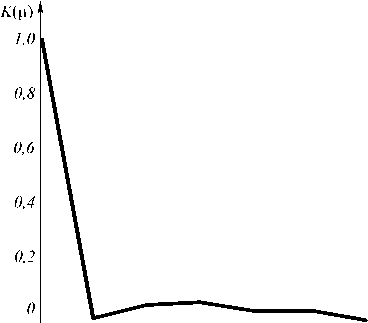
-0.2

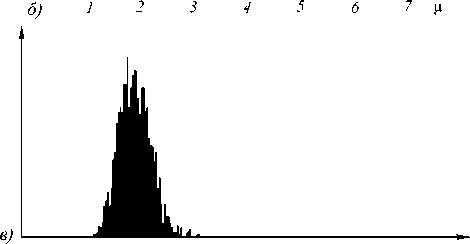
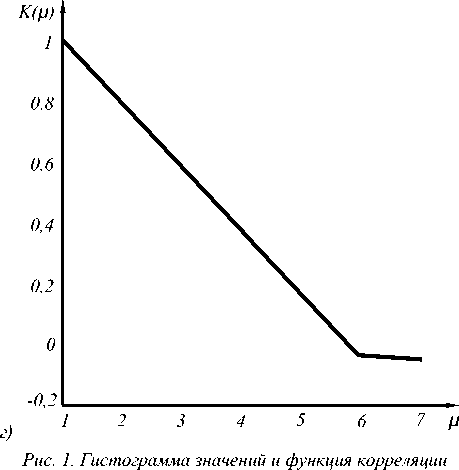
изображения ОУ до (а,б) и после обработки фильтром Lee (в,г)

Таким образом, фильтрация локальными методами позволяет повысить коррелированность соседних элементов сглаженного изображения и может быть эффективно использована для его последующей сегментации.

Целью данной работы являлось исследование эффективности применения алгоритмов сегментации на основе модели системы со случайной скачкообразной структурой [5] к когерентно-локационным изображениям после сглаживания на них спекл-шума локальными методами пространственной фильтрации.

Результаты сегментации

Исследование проводилось методом имитационного моделирования для двух классов подстилающей поверхности аналогично [5]. В качестве модели изображения применялось "шахматное" поле размером 150х150 ЭИ, сформированное в соответствии с (1). Вначале осуществлялось сглаживание спекл-шума локальным фильтром, затем – сегментация различными алгоритмами: однострочными – ОА1, ОА2 и комбинированными однострочными КОА1, КОА2, описанными в [5, 6]. Размер окон обработки фильтров был выбран равным 3x3 ЭИ для уменьшения искажения границ между однородными участками.

Ошибка в определении номера СУЭПР оценивалась величиной Рош , называемой ошибкой распознавания состояния

KL

Р ош = ^ZZ z_t , k , KL k = 1 t = 1

где L, K – размеры изображения по вертикали и горизонтали, zl,k - величина, принимающая значение нуль в случае, когда оценка номера СУЭПР θ^l,k и номер СУЭПР θl,k l,k-го ЭИ незашумленного изображения совпадают, и равная единице в противном случае. Усреднение результатов проводилось по 500 реализациям.

На рис. 2 представлены графики зависимости Р_ош от разности СУЭПР Δs ОУ (СУЭПР1=1) при обработке изображения однострочными алгоритмами сегментации (результаты для алгоритмов ОА1 и ОА2 получились одинаковыми) для двух значений некогерентных накоплений N =4 и N =7, а также двух фильтров – Lee и сигма-фильтра [7]. Видно, что при предварительной фильтрации спекл-шума сигма-фильтром ошибка оказалась несколько меньше по сравнению с фильтром Lee. Очевидным результатом является уменьшение ошибки при увеличении числа N .

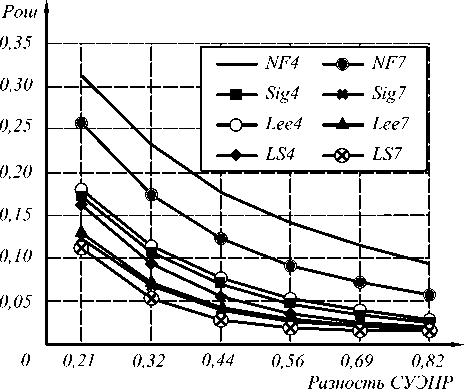
Рис. 2. Зависимость ошибки распознавания состояния от разности СУЭПР для ОА

Аналогичные графики представлены на рис. 3 для алгоритма сегментации КОА1. Из рисунка видно, что усложнение обработки приводит к уменьшению ошибки, особенно при малых значениях Δs. Ошибка продолжает уменьшаться при применении алгоритма сегментации КОА2 (рис. 4).

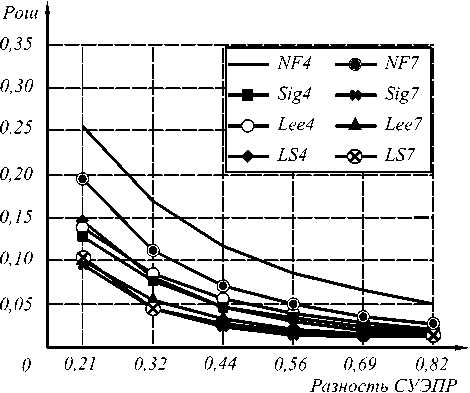
Рис. 3. Зависимость ошибки распознавания состояния от разности СУЭПР для КОА1

Рош 0,18 0,16 0,14 0,12 0,10 0,08 0,06 0,04 0,02

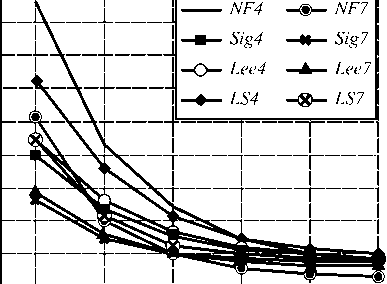
О 0,21 0,32 0,44 0,56 0,69 0,82 Разность СУЭПР

Рис. 4. Зависимость ошибки распознавания состояния от разности СУЭПР для КОА2

Из рис. 2-4 видно, что по мере усложнения обработки графики зависимости все быстрее стремятся к определенному минимальному уровню Рош , отличному от нулевого.

Наличие такого уровня обусловлено тем, что при сглаживании спекл-шума локальными пространственными фильтрами происходит искажение границы ОУ, так как размеры окон обработки фильтров конечны (3x3 ЭИ).

Известно, что с увеличением числа некогерентных накоплений N распределение (1) стремится к гауссовскому, что используется, например, при астронаблюдениях по методу Лайбери [8]. Поэтому при достаточно больших N сегментацию изображения можно осуществлять без предварительной фильтрации. В процессе исследования были получены графики зависимости Рош от Δs для случая отсутствия предварительной фильтрации (NF), представленные на рис. 2-4 для соответствующих алгоритмов сегментации. Из рис. 2,3 видно, что для алгоритмов ОА и КОА1 ошибка распознавания состояния даже при N =7 и больших значениях Δs превышает ошибку при выполнении фильтрации. Для алгоритма КОА2 при N =4 при Δs=0,69 ошибки с фильтрацией и без фильтрации становятся равными, при N =7 ошибка без фильтрации становится меньше ошибки с фильтрацией для Δs больше 0,44.

На рис. 5 приведены графики зависимости Рош от числа N для анализируемых алгоритмов с фильтрацией сигма-фильтром и без таковой при Δs =0,21. Видно, что при малых отличиях в отражательной способности ОУ подстилающей поверхности сегментация без фильтрации даже при больших N приводит к ошибкам, превышающим ошибки при выполнении фильтрации. Тем не менее, возможно применение алгоритма КОА2 без фильтрации при значениях N порядка 10 с соизмеримыми ошибками.

На рис. 6 приведены те же графики при Δs =0,69.

Видно, что при данном значении Δs ошибки распознавания для алгоритмов сегментации с фильтра- цией и алгоритма КОА2 без фильтрации соизмеримы при всех значениях N, а для алгоритма КОА1 без фильтрации ошибки соизмеримы при N больше 7.

Рош

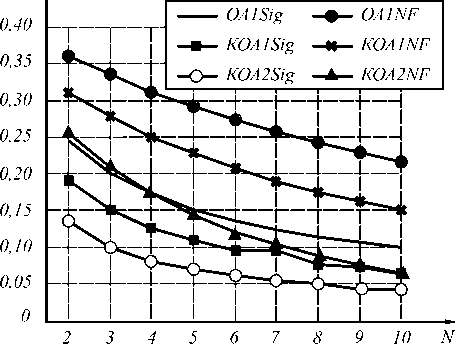
Рис. 5. Зависимость ошибки распознавания состояния от числа некогерентных накоплений N при Δs =0,21

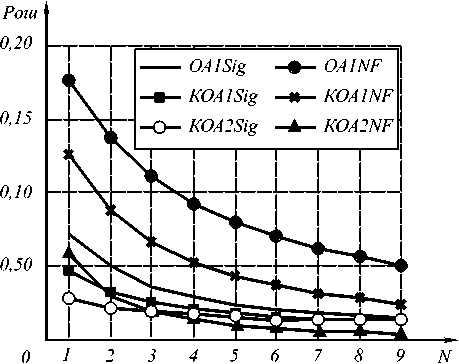
Рис. 6. Зависимость ошибки распознавания состояния от числа некогерентных накоплений N при Δs =0,69

Необходимо отметить, что характер искажений на обработанном изображении при сегментации с фильтрацией и без фильтрации несколько различен. Искажениям при сегментации изображения с предварительной фильтрацией больше подвержены граничные области ОУ, а при сегментации без фильтрации искажения проявляются по всему изображению.

Таким образом, применение локальных пространственных фильтров для сглаживания спекл-шума на изображении и алгоритмов сегментации на основе модели системы со случайной скачкообразной структурой позволяет выделять на когерентнолокационном изображении ОУ даже при их небольших различиях в отражательных свойствах. Для иллюстрации на рис. 7-10 приведены: тестовое изображение с параметрами Δs=0,32 и N =4, сглаженное фильтром Lee изображение, сегментированное изображение после фильтрации алгоритмом КОА2 и сегментированное изображение без предварительной фильтрации.

Рис. 7. Тестовое изображение

Рис. 10. Сегментированное изображение без предварительной фильтрации

Многоканальная сегментация

Повысить эффективность сегментации изображений позволяет совместное использование данных с выходов нескольких сглаживающих фильтров. При этом используется векторная форма записи уравнения сообщения, описывающего построчное формирование изображения [5]:

Рис. 8. Изображение, сглаженное фильтром Lee

Л к + 1 = Ф к °Л к + ^ k⁽ⁱ⁾

,

Рис. 9. Сегментированное изображение после фильтрации алгоритмом КОА2

где Л _к - вектор фазовых координат системы, компонентами которого являются значения яркостей на выходе сглаживающих фильтров, Ф _к ⁽¹) - известная матрица, учитывающая корреляционные связи между соседними элементами изображения, {£ _к ^{( 1} ) , к =0,1,.} - последовательность статистически независимых между собой и во времени случайных величин ^ _к ^{( 1} ) , не зависящих от случайной величины Л к в начальный момент времени и описываемых гауссовскими плотностями вероятности ^ _к ^{( 1} ) ~ N [£ _к ^{( 1} ) |0, Q^{( 1} ) ]. Процесс смены СУЭПР при переходе от одного ЭИ к другому описывается дискретной марковской последовательностью { 9_к ,}, состояния которой являются номерами СУЭПР i ( i =1,2,..., М). Предположения о статистических свойствах величин, входящих в выражение (2), аналогичны указанным в [5].

Задача состоит в нахождении оптимальной по критерию максимума апостериорной вероятности оценки номера СУЭПР j по наблюдениям {Л _к } при к =0,1,. .

Выражение для апостериорной вероятности номера СУЭПР j имеет вид:

Р ^{( Л} к ^1Л к — 1 , 0 к = j ) £ ^{п (} 0 к = j ¹⁰ к — 1 = i ^)W k — 1 ^{( 0} к — 1 = i )         ____

W k ( 0 к = j ) = Мл-----------------л ------------------------------ ( j = 1’ M ; к = 1’2--) .                          ⁽³⁾

У p ( Л к 1Л к - 1 , 0 к =в ) У п ( 0 к =рТ0 к - 1 = г ) W k - 1 ( 0 к - 1 = г )

Р= 1                            i = 1

Здесь п ( 9_к 1 9_к .1 ) - переходная вероятность, p (Л _к |Л _к - 1 , 9_к ) - условная переходная плотность вероятности.

В работе исследовалась эффективность алгоритмов сегментации при использовании двух каналов -с фильтром Lee и сигма-фильтром. На рис. 2-4 пред ставлены графики зависимости Рош от As для рассматриваемых алгоритмов (LS). Видно, что осуществление многоканальной сегментации наиболее результативно для однострочных алгоритмов: уменьшение Рош составило два процента. Для алгоритма

КОА1 уменьшение Рош составило менее одного процента, для алгоритма КОА2 многоканальная сегментация не уменьшила ошибки.

Заключение

Результаты исследования свойств алгоритмов сегментации на основе модели системы со случайной скачкообразной структурой при применении к когерентно-локационным изображениям со статистически независимыми элементами показывают возможность эффективного выделения однородных участков после сглаживания спекл-шума локальными методами пространственной фильтрации. Такое сглаживание является необходимым при малом числе некогерентных накоплений. При большом числе последних сегментация может быть выполнена и без предварительного сглаживания изображения.

Ограничением на указанную обработку изображений является нестрогое требование точности определения границ однородных участков, связанное с конечными размерами сглаживающих фильтров. Полученные характеристики эффективности алгоритмов позволяют определить ошибку сегментации при заданных параметрах локатора и подстилающей поверхности, сравнить ошибки при осуществлении сегментации в случае большого числа некогерентных накоплений, считая яркостное распределение однородных участков гауссовским, с выполнением предварительной фильтрации и без нее.