Секторное возмущение вихревого пучка: энтропия Шеннона, орбитальный угловой момент и топологический заряд

Широкое использование световых пучков, переносящих орбитальный угловой момент (ОУМ) в оптических системах передачи и обработки информации [1, 2], предполагает устойчивость их сингулярной структуры относительно слабых возмущений. Также считалось, что пучки Бесселя способны частично восстанавливать структуру при прохождении среды со слабой турбулентностью [3] даже при жёсткой фокусировке [4] или после квантового перепутывания [5]. Аналогичные свойства были обнаружены и у других типов вихревых пучков [6–8]. Однако более внимательный анализ самовосстановления пучков [9] показал, что этот процесс оказывается весьма чувствительным к типу симметрии центров возмущения. Например, Бесселевы пучки самовосстанавливаются при рассеянии на осесимметричных препятствиях, но теряют это свойство при секторном возмущении [4]. Более того, авторы работы [9] утверждают, что Бесселевы пучки не могут восстановить исходную структуру после прохождения через турбулентную среду. Сразу возникает вопрос, как оценивать степень восстановления свойств вихревого пучка? Очевидно, что такая оценка зависит от того, для каких целей и в каких оптических системах используются возмущённые пучки. Например, возмущение в виде непрозрачного правильного сектора позволяет определять топологический заряд оптического вихря [10] и ОУМ пучка [11]. Однако оно вызывает необратимое разрушение внутренней структуры оптического вихря. Важно отметить, что секторное возмущение приводит в действие принцип неопределённости между углом возмущения секторного препятствия и орбитальным угловым моментом [12, 13], что стимулирует процессы рождения и уничтожения оптических вихрей и возрастание числа новых вихревых состояний. Возрастание внутреннего беспорядка в волновой структуре указывает на необходимость использования новых статистических подходов к измерению таких физических характеристик, как информационная энтропия [14] и пространственная когерентность [15]. Проблемы анализа и измерения пространственной когерентности подробно обсуждаются в монографии Манделя и Вольфа [15]. Как правило, процесс измерений пространственной когерентности сводится к 1D-сканированию интерференционной картины в опыте Юнга, что существенно ограничивает объём полезной информации о состоянии возмущённого пучка. Изучение вопросов восстановления исходной структуры пучка [16, 17] и измерение информационной энтропии могут позволить оценить степень разрушения структуры пучка при возмущении за счёт изменения числа вихревых состояний.

Фундаментальные проблемы анализа информационной энтропии (или энтропии Шеннона) в световых пучках были рассмотрены Франсисом [14] и приложены к вихревым пучкам авторами работ [18–20]. Так, авторы работ [18, 20] теоретически оценили ве- личину информационной энтропии для 1D-отображения невозмущённого лазерного вихревого пучка и связали между собой степень пространственной когерентности и информационную энтропию. Авторы работы [19] представили экспериментальное подтверждение этих теоретических предсказаний. Было обнаружено постепенное возрастание информационной энтропии от 0 до 1 при увеличении топологического заряда вихревого пучка от 0 до 3. Такое изменение энтропии авторы связывают с ухудшением пространственной когерентности при увеличении топологического заряда пучка, которое вызвано усложнением структуры волнового фронта. Изменение числа вихревых состояний при секторном возмущении пучка непосредственно связано с принципом неопределённости между углом секторного сегмента и ОУМ [21]. Авторам работы [12] удалось подробно исследовать соотношение между неопределённостью углового положения внутри вихревого пучка и его угловым моментом. Неопределённость углового момента создавалась за счёт введения в вихревой пучок непрозрачного препятствия в виде одного сектора, вершина которого касается центра пучка. Угол сектора а служит количественной мерой угловой неопределённости. Неопределённость орбитального углового момента А^z связывалась с изменением спектра вихрей, вызванного секторным возмущением. Эти исследования были расширены в работе [13], где авторы рассмотрели Фурье-преобразование между углом и ОУМ при многосекторном возмущении лазерного пучка. Указанные исследования показали, что принцип неопределённости связывает между собой изменение пространственной когерентности, орбитального углового момента и информационной энтропии. Однако разложение возмущённого вихревого пучка по фурье-компонентам недостаточно для описания широкого спектра свойств, которые приобретает пучок. Чтобы расширить возможности анализа вихревых пучков с исходной осевой симметрией, подверженных возмущениям, мы предложили использовать представление таких пучков в виде суперпозиции мод Лагерра– Гаусса с последующим вычислением характерных параметров и выявлением новых свойств пучков.

Таким образом, в данной работе мы сфокусировались на теоретическом и экспериментальном исследовании связи между спектром вихрей, ОУМ и энтропией Шеннона при секторном возмущении вихревого пучка.

• 1.    Компьютерное моделирование секторного возмущения

Рассмотрим прохождение скалярного пучка Ла-герра – Гаусса LG ₀ ^m низшего порядка с азимутальным индексом (топологическим зарядом вихря) m через оптический транспарант с непрозрачным сектором и углом а , показанным на рис. 1. Вершина сектора касается оси пучка. Поле пучка в исходной плоскости z =0 представим в виде

V m ( r , ф , а ) = ( р / w )me^{im ф} e ^р 2 w ² = = r m e im ^ф e ^{- r 2} , а<ф< 2 л-а ,

где r = р / w , w - радиус перетяжки пучка в плоскости z = 0, р и ф - полярные координаты.

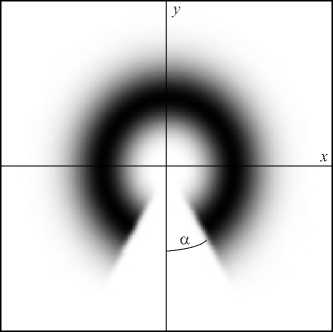
Рис. 1. Геометрия вихревого пучка ¥ m (r, ф ) в плоскости z = 0

Представим поле, модулированное по азимутальному углу ф , в виде разложения по ненормированным LG p^m модам:

да

Vm (r,ф, а)= £ Cm,n (а)LG0 (r,ф) = n=-да да

= £ C m , n ( а ) r n e in ^ф e ^{- r 2} , n =-да

где амплитуды мод

^| n|+1 2п-а                  да cmn (а) = -         ei(m-n)фdф rm+n+1 e-2r2dr =

, v п n!                       0(-1) m^n г

H + ti + 1 lx

m - n п — а

I -------г

п ^ 2 sinc[(m - n)(л-а)] x---r^^Z7—7^  , где а < п, Г(x) - гамма-функция. Члены ряда (2) с радиальными индексами p ^ 0 исчезают в силу ортогональности LG мод. Возмущённый пучок (2) вдали от исходной плоскости z =0 запишется в виде да

V m ( r , ф , z , а ) = ^ C m , n ( а )

n =-да

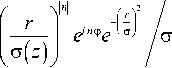
( z ) ,(4)

где g ( z ) = 1 - iz / z о , z о = kw ² /2 - длина Релея, k - волновое число.

На рис. 2 представлено компьютерное моделирование распределения интенсивности 3(r, ф, z = 0) и фазы Ф(r, ф, z = 0) вихревого пучка с топологическим зарядом m = 10, подвергнутого секторному возмущению с углом сектора α. Чётко выделяется область секторного препятствия. Основной световой поток образует характерную подкову, концы которой размыты, а вдоль поверхности видна слабая «рябь». Наиболее ярко искажения волнового поля отображает распределение фазы. Локализацию вихрей можно связать с концами нодальных линий в распределении фазы. Слабое возмущение α ≈ 1° приводит к расщеплению вырожденного вихря m = 10 на ряд единичных вихрей внутри подковы. Одновременно рождается облако вихрей, окружающих подкову. Увеличение угла возмущения α приводит к перестройке фазовой картины таким образом, что вихри внутри подковы стараются сохранить её форму подобно тому, как строится изображение букв в лазерных пучках в работе [22]. Естественная локализация вихрей позволяет сохранить форму возмущённого пучка при распространении с точностью до масштаба и поворота, как показано на рис. 3. Однако число нодальных линий внутри подковы не совпадает с топологическим зарядом невозмущенного пучка из-за проникновения дополнительных вихрей внутрь подковы, вызванных дифракцией на краях апертуры. И это было подтверждено нашим компьютерным моделированием, которое не обнаружило признаков самореконструкции вихревого пучка ни при каких значениях секторного угла α.

угол α

Интенсивность

ℑ ( r , ϕ ) (теория)

Интенсивность

ℑ ( r , ϕ ) (эксперимент)

Фаза Ф( r , ϕ )

α =1°

α = 120°

Рис. 2. Теоретическое и экспериментальное распределение интенсивности (инверсия) ℑ (r, ϕ ) и фазы Ф(r, ϕ ) возмущённого вихревого пучка с исходным топологическим зарядом M = 10 в плоскости z = 0 в зависимости от угла сектора α . Координаты x и y заданы в безразмерных единицах

Как мы показали в работах [23, 24], анализ спектра вихрей (зависимость интенсивности вихревой моды в сложном пучке от топологического заряда) позволяет восстановить исходный пучок и его ОУМ.

Воспользуемся этим подходом для исследования ОУМ и информационной энтропии.

Интенсивность

Z = z / z 0

Эксперимент

Фаза

Ф( r , ϕ )

Z =1

ℑ ( r ,ϕ)

Z =5

Z =15

Рис. 3. Эволюция интенсивности (инверсия) ℑ (r, ϕ ) и фазы Ф(r, ϕ ) вихревого пучка с топологическим зарядом M = 10 вдоль ось Z = z / z 0 , подвергнутого секторному возмущению с углом α = 45° (теория и эксперимент).

Координаты x и y заданы в безразмерных единицах

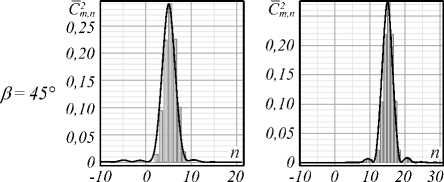
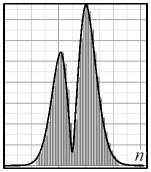
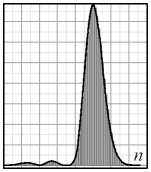
Спектры вихрей . Заметим, что при построении поля возмущенного пучка мы использовали амплитуды мод C m , n , полученные из выражения (3), где функция поля мод Ψ n не нормирована. При этом результаты компьютерного моделирования и эксперимента хорошо согласуются (рис. 2, 3). Однако при вычислении ОУМ и информационной энтропии следует использовать амплитуды С m ², n , полученные при условии нормировки Ψ m [25]. Между этими амплитудами существует простое соотношение С m ², n = 2 ^{-| n |-2} | n |! С m ², n . Чтобы наглядно подчеркнуть действие секторного возмущения на вихревой пучок, мы разместили на рис. 4 две серии спектров вихрей C m 2, n ( α ) для исходных топологических зарядов m =5 и m = 15.

Анализ вихревых спектров показал, что в интервале углов α ∈ (0,45°) происходит очень вялая перекачка энергии из основной гармоники с m =5 и m = 15 в соседние моды. Огибающая дискретного спектра почти симметрична относительно центральных основных мод. Спектральные сателлиты располагаются в положительной области топологических зарядов мод n >0.

Однако по мере увеличения угла α (уменьшения смежного угла β = π – α ) симметрия нарушается. После угла α = 90°, при котором вырезается половина светового потока, в отрицательной области спектра n <0 наблюдается зеркальный максимум.

Уменьшение угла β сопровождается интенсивной перекачкой энергии в вихревые моды с отрицательными топологическими зарядами. Из сравнения спектров для m =5 и m = 15 видим, что перекачка энергии в моды с n <0 происходит более интенсивно для пучков с меньшими топологическими зарядами |m|. Сто- ит отметить, что аналогичные измерения проводили авторы работы [13], проверяя оптический принцип неопределённости между азимутальным углом и ОУМ. Авторы не обнаружили формирования дополнительного массива вихревых мод с n <0. Это связано с тем, что ими исследовались топологически нейтральные пучки m = 0 и m = 2 при угле 2р = 45°. Как мы показали, при этих условиях возникновение второго спектрального максимума невозможно.

0.06

0,06

0,04

0,04

в = 6°

0,02

0,02

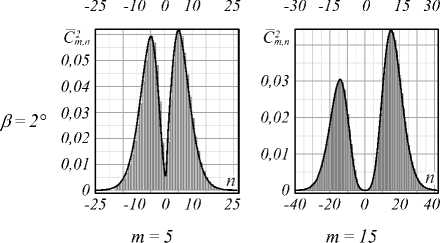
Рис. 4. Дискретный спектр вихрей C _m ² _,n ЛГ-пучков с топологическими зарядами m = 5 и m = 15, возмущенных секторной диафрагмой со смежным углом сектора в = п - а .

Сплошная линия – огибающая дискретного спектра

Топологический заряд . По определению топологический заряд монохроматического пучка задаётся полным числом оптических вихрей в поперечном сечении светового потока с учётом их знаков и вычисляется контурным интегралом на комплексной плоскости [26]. М. Берри свёл данный интеграл к виду, удобному для вычислений (см. формулу (21) в работе [25]):

1      2r      д

M =    hmfdQ—arg Y _m ( r , ф , a ) =

2 п r о дф

2п

1 Г = —Re <  lim d ф 2 п      ^r ^” '

X

£ nCm,n (a)rneinф n=-X____________________

N

• 2    C m,n ( a ) r n e in ^K

n =-X

Мы провели ряд компьютерных оценок топологического заряда возмущённого пучка (1) для различных исходных топологических зарядов. При этом использовались следующие ограничения. Как показывают спектры вихрей на рис. 4, квадраты амплитуд мод быстро стремятся к нулю по мере возрастания их топологического заряда n :

lim C m , _n ^ 0 . n ^X

Поэтому можно ограничиться конечным числом мод | n _ma x |= N , при которых C m _n ~ 10 -3 . Радиус полуширины пучка можно оценить по формуле положения максимума интенсивности исходного вихревого пучка r_N = ^ | N |/2 . Поэтому в (5) мы заменили предел r ^ да на r ^ 3 r_N . Результаты компьютерного моделирования приведены на рис. 5. Из рис. 5 видно, что общий топологический заряд M при a = 3 п /4 остаётся равным исходному топологическому заряду невозмущённого пучка N = m .

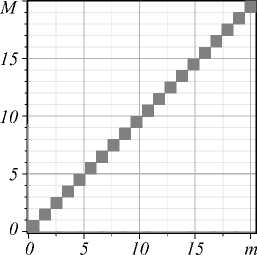
Рис. 5. Компьютерное моделирование выражения зависимости полного топологического заряда M возмущенного пучка от топологического заряда m исходного пучка. При вычислениях учитывалось, что максимальное число вихрей в пучке n max = 20 c квадратом амплитуды C mm _n ~10 - ³

и в формуле (5) принято r ^ 10

Компьютерные расчёты для углов секторной диафрагмы a = п /4, п /2, 30 п /31 показывают аналогичные результаты. Поэтому мы предполагаем, что и в общем случае произвольных углов a будет выполняться сохранение исходного топологического заряда при секторном возмущении.

Именно этим свойством воспользовались авторы работы [10] для экспериментальной оценки топологического заряда при секторном возмущении. Хотя авторы не оценивали топологический заряд возмущённого пучка, они заметили, что при определённых секторных углах a , число максимумов в «подкове» распределения интенсивности равно исходному топологическому заряду пучка.

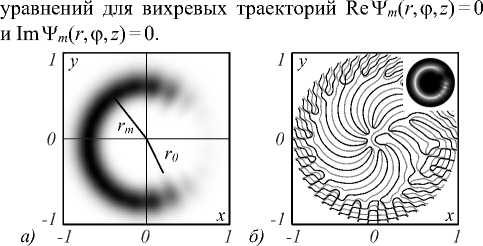
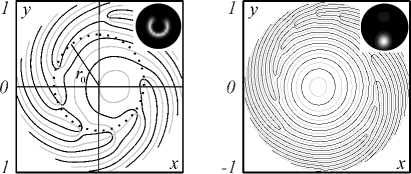
Сразу обратим внимание на тот факт, что топологический заряд возмущённого вихря M и число вихрей, возникших при возмущении, являются совершенно разными физическими характеристиками. Рассмотрим этот вопрос подробнее. Вообще говоря, положение центров вихрей определяется решением

• в)                                г)

Рис. 6. Распределение интенсивности z = 0

и а = 5 п /24рад=17,5° (а). Положение центров вихрей на линии пересечения поверхностей Re У т = 0 и 1т У т = 0 для Z = 0,5 (б), Z = 7 и а = 17,5° (в), Z = 15, а = 170° ( в = 10°)(г)

Сечение траекторий плоскостью наблюдения z = z obs задаёт положение центров вихрей. Результаты нашего компьютерного моделирования для возмущённого пучка с топологическим зарядом m = 10 приведены на рис. 6. Видим, что число вихрей в области наблюдения быстро изменяется с изменением секторного угла а и положения плоскости наблюдения z = z obs . Вблизи плоскости перетяжки Z =0,5 и а = 5 п /24=17,5° (рис. 6 б ) наблюдается 8 центров вихрей в окрестности оси пучка, окружённых множеством вихрей на периферии, но число наблюдаемых максимумов только четыре. В волновой зоне Z =7 (рис. 6 в ) число максимумов совпадает числом нулей поля в окрестности оси. Переход к дальней зоне дифракции Z = 15 сопровождается исчезновением наблюдаемых максимумов (на рисунке не показано).

Увеличение секторного угла а (уменьшение смежного угла р ) на рис. 6 г приводит к резкому увеличению числа наблюдаемых вихрей. С другой стороны, формула (5) показывает, что амплитуды вихревых мод C m , n не зависят от амплитуды, т.е. топологический заряд m не связан с числом вихрей в возмущённом пучке. На первый взгляд, это противоречит привычным представлениям о вихревых пучках. Но следует помнить, что формула (5) задаёт топологический заряд исходного поля m , который называют топологическим зарядом при условии, что возмущение не вносит истоков или стоков ОУМ (как, например, оптический клин [27], оптическое волокно [28] или анизотропная среда [29]).

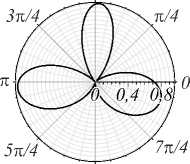
В противоположность авторам работы [10] мы исследовали положение вихрей в области дифракционной полутени внутри подковы возмущённого пучка. Для этого мы сканировали азимутальное распределение интенсивности на расстоянии r 0 от оси пучка (см.

рис. 6а). Результаты сканирования приведены на рис. 7а, б в полярных координатах. Число лепестков кривых совпадает с исходным топологическим зарядом m. Поскольку по мере увеличения топологического заряда положения вихрей может значительно смещаться от окружности сканирования r = r0, размеры внутренних лепестков существенно отличаются от внешних лепестков. Кроме того, в область наблюдения попадают вихри, возникшие на краях секторной апертуры. Поэтому следует ожидать, что эксперимен- тальная регистрация топологического заряда для пучков с m >7 окажется затруднительной.

а)

л/2

в)

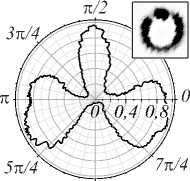
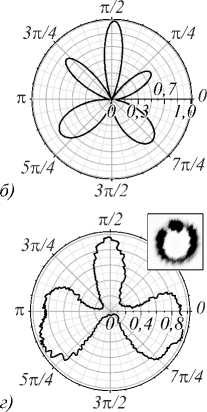
Рис. 7. Азимутальное распределение интенсивности 3 (r a , ф ) на расстоянии r 0 от оси вихревого пучка в дальней зоне дифракции для различных топологических зарядов m при угле сектора а~ 15°: теория т = 3, Г 0 = 3 (а); т = 5, r 0 = 6,5 (б); эксперимент m = 3 (в), m = 5 (г). На выноске приведены изображения пучков в плоскости сканирования

Орбитальный угловой момент . В отличие от топологического заряда пучка ОУМ чувствует изменение числа вихрей, вызванное произвольным возмущением. Действительно, ОУМ на фотон возмущённого пучка задаётся формулой [25]

да                                да fcz (а, т) = ^ nCn2 (а, т) / ^ СП (а, т) = n=-да                   n=-да да                                                              да

• = ^ n [ C_n n ( а , т ) — С -2 n ( а , т ) ] / ^ С П ( а , т ) . n =1                                           n=-да

  
  

Заметим, что использование термина спектр ОУМ в тексте эквивалентно зависимости ОУМ fc z либо от секторного угла а , либо от исходного топологического заряда вихревого пучка, в то время как термин «спектр вихрей» подразумевает зависимость квадратов амплитуд мод С m ², n от топологического заряда мод при заданных значениях секторного угла а и исходного топологического заряда m вихревого пучка.

Из выражения (5) видим, что спектр ОУМ однозначно задаётся вихревыми модами Сn2 , так что всякие изменения в спектре вихрей немедленно отражаются на спектре ОУМ. Действительно, для возмущённых состояний |т) = |5), |10) и |15) ОУМ fcz(а) практически не изменяется (рис. 8а) в широком интервале секторных углов а = (0°,90°), поскольку нет существенных изменений в спектре вихрей. В этом интервале происходит очень слабая перекачка энергии в спектрах Сm2,n на рис. 4а, б, которая в основном сказывается на «хвостах»: в спектре вихрей на рис. 4. Существенные изменения ОУМ наступают при углах р >45°, когда начинает формироваться второй максимум в спектре вихрей Сm2,n. По мере притока энергии во второй максимум ОУМ стремительно уменьшается, так что при р® 2° интенсивности в спектральных максимумах уравниваются, а ОУМ снижается до нуля.

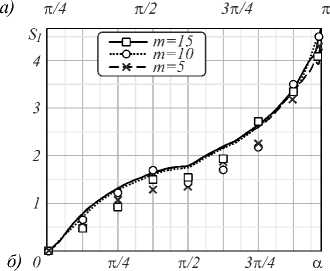
Рис. 8. Компьютерное моделирование ОУМ .( а , т) (а) и энтропии Шеннона S i ( a т) (б) для топологических зарядов m = 5, m = 10, m = 15 (линии) крестикам ( × ), кружкам ( О ) и квадратикам ( □ )

соответствуют эксперименту

Энтропия Шеннона (информацион н ая энтропия) . Нормированный квадрат амплитуды С „ ² е (0,1) (3) в разложении (2) волновой функции поля (1) по вихревым модам можно рассматривать как условную вероятность P ( n / m ) встретить вихревой пучок в состоянии | n ) при условии, что на состояние | т ) подействовало внешнее возмущение а [15] (т.е. P ( n / т ) = С ²( а , т )). Такой вероятностный подход учёта числа вихревых состояний можно использовать в формуле Шеннона.

Ещё в 1948 году Клод Шеннон [14] предложил учитывать меру потери информации (меру неопределённости), возникающую при действии возмущения на информационный канал за счёт перераспределения энергии по другим каналам, формулой

N

S I = - ^ P ( n / т ) log ₂ P ( n / т ) . (7) n =0

Учитывая выше сказанное, формулу (7) можно переписать в терминах квадратов амплитуд (интенсивностей) вихревых мод

N

S i =- ^ С ( а , т ) log 2 С П ( а , т ) .               (8)

• n =0

• 2. Эксперимент и обсуждение результатов

Энтропия S I является действительной положительной величиной и изменяется в широком интервале значений 0< S I < ∞ при изменении квадратов нормированных амплитуд в интервале 1 >  С П ( а , т ) >  0. На рис. 8 б показана зависимость энтропии S I от угла а для различных топологических зарядов т . В отличие от ОУМ информационная энтропия возрастает уже при сравнительно небольших углах возмущения а , поскольку число возбуждённых вихревых состояний возрастает, хотя переносимая ими энергия мала. При а = 90° скорость изменения энтропии (направление касательной к кривой S I ( а )) изменяется, поскольку скорость рождения новых вихревых состояний начинает быстро возрастать. Характерно, что на этом интервале углов кривые S I ( а ) для различных т почти совпадают. Это указывает на идентичность процессов возбуждения вихревых состояний для различных топологических зарядов. Кривые S I ( а ) расщепляются в области углов р ~10°, поскольку генерация новых вихревых состояний происходит быстрее для пучков с большими топологическими зарядами. Заметим, что информационная энтропия характеризует изменение числа вихрей в возмущённом пучке. Если ОУМ £_z характеризуется относительным вкладом разности интенсивностей вихревых мод с противоположными знаками топологических зарядов (см. формулу (6)), то энтропия Шеннона S I учитывает полное число вихрей возмущённого пучка.

Мы поставили задачу измерения спектров вихрей и на их основе анализа изменения энтропии и ОУМ в сложном вихревом пучке при слабых и сильных секторных возмущениях для вихрей с различными топологическими зарядами. Основная идея измерительного процесса заключалась в разделении пучков как по величине, так и по знаку топологического заряда. Если голографические методы позволяют осуществлять этот процесс, разделяя пучки с различными топологическими зарядами m в 3D-пространстве по направлениям распространения вихревых мод (см., например [30, 31]), то в нашем случае такое разделение осуществляется в виртуальном пространстве компьютера в соответствии с откликом вихревых мод на моменты интенсивности высших порядков [23, 24, 32]. Одним из основных требований измерений является способность метода разделять вихревые пучки по знаку топологического заряда. Если для анализа спектра вихрей методом моментов интенсивностей с одним знаком топологического заряда достаточно ограничиться измерением лазерного пучка в фокальной плоскости сферической линзы [23, 24], то для измерения спектра смешанных массивов вихрей необходимо использовать дополнительные астигматичные преобразования пучка [32]. Такую астигматичнную операцию выполняет цилиндрическая линза CL (рис. 9). Цилиндрическая линза в плоскости двойного фокуса преобразует пучок Лагер-ра – Гаусса (ЛГ) в пучок Эрмита – Гаусса (ЭГ). ЛГ-пучки с противоположными знаками топологических зарядов формируют ЭГ-пучки с ортогональными осями астигматизма. Число нулей функции ЭГ равно топологическому заряду единичного ЛГ-пучка. Далее смешанный массив вихрей анализируется методом моментов интенсивности [33].

Для формирования возмущённых вихревых пучков мы отказались использовать секторные голограммы на пространственном модуляторе (SLM), как это делалось в работах [10, 12, 13], поскольку при измерениях моментов интенсивности высших порядков возникали большие погрешности из-за неучтённых краевых эффектов на секторных голограммах. Вместо этого использовалась металлическая секторная диафрагма (D) с регулируемым углом сектора, которая устанавливалась непосредственно перед цилиндрической линзой (CL), как показано на рис. 9. Таким образом, сначала на SLM-модуляторе формировался ЛГ-пучок с заданным топологическим зарядом m . Затем секторное возмущение с заданным углом α создавалось диафрагмой (D) и преобразовывалось цилиндрической линзой CL, и далее регистрировалось CCD-камерой, установленной в плоскости двойного фокуса CL-линзы. Спектр вихрей выводился на экран монитора после соответствующей обработки изображения пучка. Для измерений использовался SLM-модулятор типа (Thorlabs EXULUS-4K1) и ССD-камера типа (Thorlabs DCC1645).

т=—10

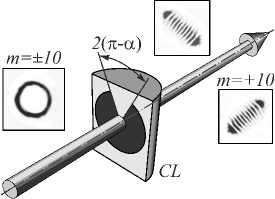
Рис. 9. Эскиз секторной апертуры (D) в плоскости цилиндрической линзы (CL)

Топологический заряд . Сначала исследовалась устойчивость формы возмущённого пучка относительно распространения из волновой в дальнюю зону дифракции. На рис. 2 представлены изображения возмущённого пучка с различным углом возмущения α . Возмущение с секторным углом α≈ 1° практически не изменяет форму пучка за исключением небольшого участка «прокола» пучка. При больших углах возмущения возникает изображение в виде подковы с размытыми краями. В процессе распространения средняя форма пучка сохраняется с точностью до масштаба и поворота.

Как показало компьютерное моделирование, оптические вихри локализуются в области дифракционной полутени вблизи внутренних краёв подковы. Для детектирования их положения требовалось решить проблему высокого градиента интенсивности при переходе из области r m в область r 0 (рис. 6 а ).

Для решения этой проблемы использовался метод псевдоцветов [34]. В этом методе присвоение пикселям разных цветов осуществляется в результате градации по уровням яркости. В данной работе использована дискретная настраиваемая палитра, в которой первоначальные компоненты цвета (R, G, B) выбираются с помощью датчика случайных чисел. Измерения показывают, что использование палитр случайных цветов позволяет хорошо выделять мельчайшие детали изображения, но при этом теряется информативность самого цвета. Кроме того, при большом числе цветов в палитре теряется связность изображения, происходит его кластеризация. Тем не менее, удобно брать случайные палитры в качестве основы, а затем вручную заменять некоторые цвета палитры. Таким способом можно достичь очень высокой детализации изображений даже в затемнённых областях, которые глаз воспринимает как чёрное пятно.

Компьютерная программа реализована нами на языке C# и позволяет быстро обрабатывать изображения размером до 100 Мб, «на лету» осуществлять замену цвета в палитре и использовать в дальнейшем настроенные палитры цветов. Идея использования псевдоцветов не является новой и широко используется на практике. Средства визуализации, основанные на псевдоцветах, имеются, например, в MATLAB, где содержится более 15 специальных палитр для визуализации значений двумерных и трёхмерных матриц [34].

В качестве примера калибровки цветов на рис. 10 представлено изображение вихревого пучка с m =3 и возмущением α = 15°.

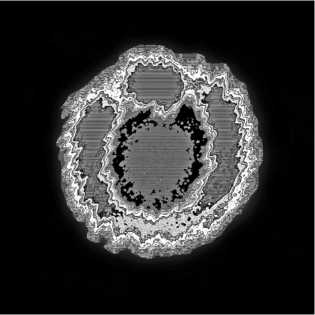
Рис. 10. Калибровка цветов для детектирования локализации вихрей внутри подковы пучка с m = 3 и α = 15°

Для сканирования изображения потребовалось провести дополнительное размытие изображения с помощью электронного фильтра, импульсной переходной функцией которого является функция Гаусса. Положение радиуса сканирования r0 подбиралось вручную в области внутренней полутени таким образом, чтобы график зависимости интенсивности ℑ от азимутального угла ϕ имел наиболее приемлемую форму для анализа. В результате сканирования получаем в полярных координатах замкнутую кривую, число лепестков которой равно топологическому заряду m невозмущённого пучка. На рис. 7в, г представлены кривые для топологических зарядов m =3 и m =5. Нам не удалось получить приемлемые для анализа кривые для m >7, поскольку при высоких значениях топологического заряда положения вихрей значительно смещены относительно окружности сканирования r = r0, а размеры лепестков становятся сравнимыми с уровнем спекл-шума.

Спектр вихрей. В процессе измерений спектра вихрей Cm2, n (а) возмущённого пучка появлялся большой массив оптических вихрей. Число вихрей зависит как от исходного топологического заряда m, так и от угла возмущения а. Например, при угле в = п - а = 25° в возмущённом пучке в состоянии |5) участвуют N = 19 вихрей с интенсивностью не ниже 0,05, при угле р«6° уже возникает ^~41 вихрь с относительной интенсивностью не менее чем 0,05. Чтобы сравнить результаты компьютерного моделирования с экспериментом, мы построили огибающие дискретных спектров вихрей. Результаты компьютерного моделирования и эксперимента приведены на рис. 11. Сравнение кривых на рисунке показывает хорошее согласование теории и эксперимента. Погрешность измерений зависит от числа вихрей в спектре. Так, при возмущении а =135° в пучке с m = 5 присутствует N = 11 вихрей, и погрешность измерений составляет 6%, в то время как возмущению а = 173° соответствует N =41 вихрь, и погрешность снижается до 2%.

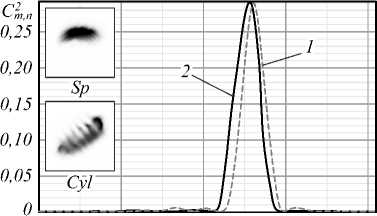
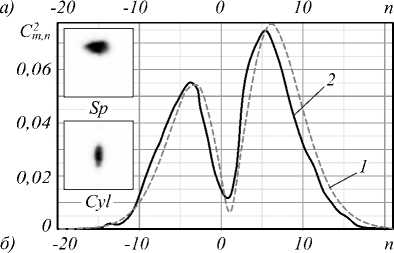
Рис. 11. Огибающие дискретного спектра вихрей с m=5 :

а =135° (а) и а =173° (б); (1) теория, (2) эксперимент.

Выноски: снимки пучка после сферической линзы (Sp) и в плоскости двойного фокуса цилиндрической линзы (Cyl)

Орбитальный угловой момент. Результаты измерений ОУМ и эксперимента представлены на рис. 8а в виде экспериментальных точек вблизи соответствующих теоретических кривых. При небольших углах возмущения а наблюдается небольшое рассогласование теории и эксперимента. Если ОУМ при компьютерном моделировании мало отличается от исходного топологического заряда fcz« m, то измерения ОУМ дают отклонение в пределах 6%. Однако это рассогласо- вание быстро сокращается с увеличением секторного угла. Мы относим возникшую погрешность на счёт несовершенства краёв апертурой диафрагмы.

Энтропия Шеннона . Экспериментальные точки зависимости энтропии S i от секторного угла а были получены при помощи формулы (8) с учётом спектра вихрей C m 2, n ( а ). Результаты измерений довольно точно повторяют ход теоретических кривых на рис. 8 б . Чётко прослеживается резкое возрастание энтропии при больших углах возмущения, которое отражает возникновение лавины вихрей на рис. 4.

Заключение

Исследовано преобразование спектра вихрей, топологический заряд, ОУМ и энтропия Шеннона (информационная энтропия) при секторном возмущении вихревых ЛГ-пучков высших порядков. Была построена модель секторного возмущения, проведены компьютерные вычисления и экспериментальные измерения на основе метода моментов интенсивности. Используя компьютерные оценки для малых, средних и больших секторных углов, мы предположили, что топологический заряд остаётся постоянным при любой величине секторного возмущения и будет равным топологическому заряду невозмущённого пучка. Был предложен метод и проведены измерения топологического заряда на основе компьютерной модели многошаговой градации цветов. Исследование спектров вихрей показали, что изменением спектра вихрей управляет оптический принцип неопределённости между углом секторной апертуры и ОУМ, который существенно сказывается на спектре вихрей при очень больших секторных углах. При малых углах секторной диафрагмы в формировании спектра участвуют вихревые пучки с одинаковым знаком топологического заряда, однако при больших углах возмущения в отрицательной области топологических зарядов формируется зеркальный максимум. При очень больших углах секторного возмущения возникает лавина вихрей, которая способствует почти одинаковому перераспределению энергии между двумя максимумами.

Изменение ОУМ сопровождается преобразованием спектра вихрей. Поскольку ОУМ зависит не от интенсивности каждого модового пучка, а от разности интенсивностей модовых пучков, то при малых углах возмущения он почти численно совпадает с топологическим зарядом исходного вихревого пучка, но при больших углах возмущения, когда вклад вихревых мод с противоположными топологическими зарядами почти уравнивается, ОУМ быстро стремится к нулю. Энтропия Шеннона определяется числом вихрей, вызванных возмущением. Поэтому по мере увеличения угла возмущения энтропия монотонно возрастает.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-2901233; гранта №ВГ24/2018 «Крымский федеральный университет имени В.И. Вернадского».