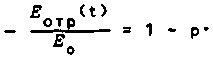Секвентные сигналы в зондировании поглощающих сред

В последние годы наблюдается повышение интереса к диагностике различных объектов с помощью коротких электромагнитных импульсов. При этом возможности дифракционной диагностики позволяют, как правило, выявить искажение геометрической формы исследуемого объекта. Изменение внутреннего состояния (например, поглощающих свойств) может быть выявлено анализом изменения профиля отраженного сигнала, несущего в себе информацию о параметрах вещества. 8 данной работе рассматривается возможность диагностики поглощающей среды по отклику секвент-ного импульса (без несущей). Анализируется нетрадиционная особенность фазового профиля Фурье-гармоник отраженного сигнала. Получены простые аналитические выражения, характеризующие деформацию профиля отраженного сигнала для случая, когда длительность импульса велика по сравнению с характерными временами релак- сации среды. Демонстрируются численные результаты описания деформации профиля при произвольной длительности секвентного импульса. Полученные результаты могут применяться в инженерных задачах диагностики состояния плазмоподобных сред.

Пусть из полупространства z > 0 на среду (z<0) под углом а падают S-поля ризованный прямоугольный импульс длительностью Т без несущей

Е пад

Е_о для |tI < Т/2 0 для 11 | > Т/2

При этом поле отраженной волны может быть представлено в виде

Е (t) = / R Е • e"'“^t»dco, отр               со со              '

go -sin (соТ/2)

где Е = ------------- - Фурье-компонента падающей волны (1):

“             тссо

Е (t) =  / Е »е 1Mt»dco, a R - коэффициент отражения фиксированной гар пад        со       'со моники [ 1] :

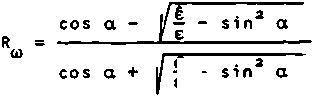
е где е - диэлектрическая проницаемость полупространства z > 0 (в дальнейшем по лагаем е = Ео вакуума), Е - диэлектрическая проницаемость среды z < 0, для ко торой используем плазменную модель 2

*П

Е = 1__л(4)

Е          со» (со+ iv) '

о е N                      11/ е 1

где О = (------ )  = 5,64'10    |/(-------- ) (—) - Лэнгмюровская частота (N - кон л m -е                        / ,пао — з се е о                           у 1 0 м центрация электронов), у - эффективная частота столкновений электронов.

8 реальных экспериментах диагностику параметров среды (у) целесообразно

лроводить ,

зондируя ее импульсами, характерные частоты которых

/ 2п . (со - -у )

неве -

лики. В частности, можно получить аналитическое решение для отраженной волны

в случае б = max—, —  « 1 . При этом из ( 3 *  ,

I °л I еания, имеем

опуская громоздкие преобразо-

рш = (1 - I f I + 6) -е1 (n+f+6    > ,

где f = sign (со)

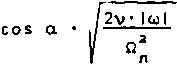
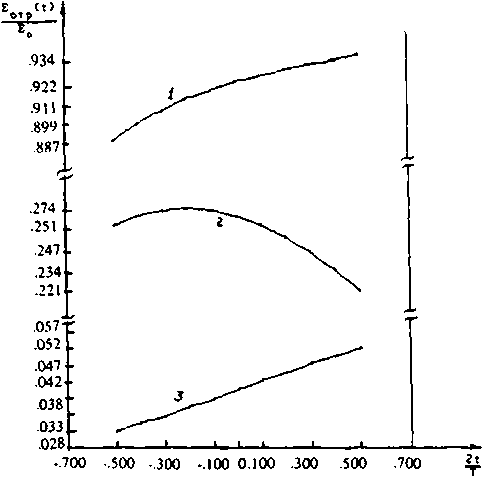
8 полученных выражениях (5*6) следует отметить нетрадиционную особенность i

Фазы коэффициента отражения R^ = I Rl -е , а именно ср - VTo". Обычно (при наличии несущей частоты соо) фаза раскладывается в ряд: Фш = Фо + Ф0»(со - со0) * ср"

+ ^(со - coQ) + . . . . При этом фд характеризует [2] временную задержку отраженного сигнала (т.е. время пребывания его в среде, или глубину проникновения), а Ф , ср и т.д. - искажение его формы. В нашем случае (когда <р - V со ) для нулевой несущей частоты имеем <р0

т . е

нулевая частота вообще не вернется из среды

как и должно быть). Однако ее доля

в спектре интеграла (2) невелика

и поз-

воляет получить конечный результат

суперпозиции всех

околонулевых частот. Дей-

ст вительно

вводя р

П л

при р « 1 вблизи

центра отраженного сигнала

получим

nd + ^)

(см. кривую

на рисунке). В частности, экспериментально

регистрируемое смещение

ЕЕ центра -=-

dE

сигнала

Е

Ео

/dt

Ео

Е

о

связаны друг с другом

Р

и темп нарастания поля в центре

отраженного

ЕЕ dE 7dT

Эта самосо-

гласовэнноеть может служить критерием корректности модели, что позволяет уве-

ренно восстанавливать экспериментальное р, получая в конечном итоге

4 cos2 а

В случае сверхкоротких импульсов, когда 6 -1, задача становится трехпараметрической. При этом вводя pi - -■ у и Ра « ^— для а = 0 численное интегриро-л              л вание (2-4) приводит к кривым 2,3 (см. рисунок).

Характерные зависимости поля отраженной волны от времени при а ^ 0:

кривая 1 - (р=0) - аналитическая форма (7);

кривая 2 - (р₁=1, р₃=0,5 (р=1); кривая 3 -(_Pi=0,5, р₃=10 (р=3,16>