Семантика и семантически эквивалентные трансформации UML-диаграмм классов

В связи со всё нарастающей сложностью современных программных систем (ПС) возникает потребность в формализации процесса проектирования архитектуры программного обеспечения. Подобная формализация позволит повысить степень автоматизации данного процесса.

Для проектирования архитектуры программного обеспечения часто используется унифицированный язык моделирования UML (Unified Modelling Language), позволяющий производить визуальное проектирование, документирование и формальное описание программных систем.

К преимуществам использования UML можно отнести наличие развитых средств проектирования UML-моделей (Enterprise Architect, Visual Paradigm и др.) и чётких общепринятых стандартов (стандарты группы OMG).

Язык UML позволяет проектировать архитектуру ПС, в том числе в рамках объектноориентированной парадигмы программирования. Модель ПС описывается в виде набора связанных между собой диаграмм (классов, прецедентов, компонентов, последовательности и т.д.) Каждая диаграмма состоит из элементов (классов, интерфейсов, пакетов, объектов и т.д.), связанных между собой отношениями (наследование, агрегация, зависимость и т.д.).

Для проведения исследований в области эволюционного проектирования объектноориентированной архитектуры ПС необходимо создание формальной теории, описывающей объектно-ориентированную архитектуру ПС и её семантику.

В статье описывается формальная семантика UML-диаграмм классов, на основе которой возможно выполнять сравнение двух диаграмм классов между собой, проверять инвариантность семантического значения после трансформаций в ходе эволюционного поиска (рис. 1).

На рис. 1 приведён пример семантически эквивалентной трансформации UML-диаграммы классов, заключающейся в введении для классов Designer (Дизайнер), Secretary (Секретарь) и Manager (Менеджер) с одинаковым набором полей: id (уникальный идентификатор), FIO (ФИО), address (адрес), positionID (идентификатор должности), salary (заработная плата) – вводится родительский класс Employee (сотрудник) с набором полей id, FIO, address, positionID, salary, от которого их наследуют классы Designer, Secretary и Manager.

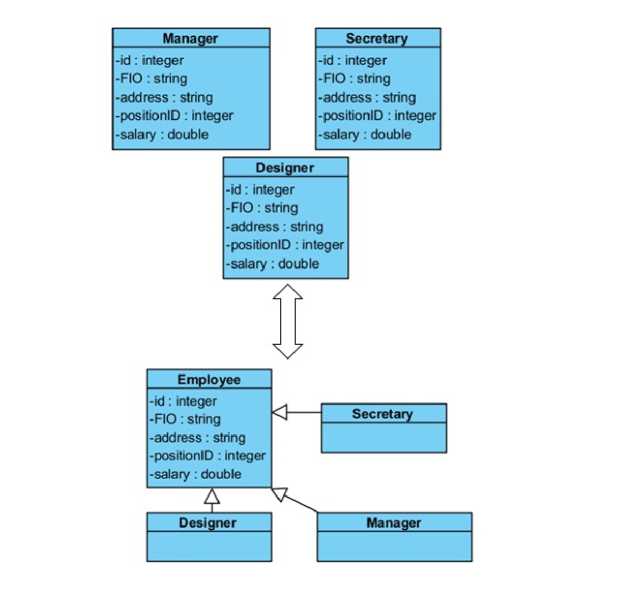
Рис. 1. Пример эквивалентной трансформации UML-диаграммы классов

• 2.    Эволюционное проектирование объектно-ориентированной архитектуры

Объектно-ориентированное проектирование начинается с описания функциональности системы, а затем перечисления основных классов, методов и атрибутов, задания основных интерфейсов и иерархий наследования. Часто удобно применять готовые паттерны проектирования [1].

Различные подходы к объектно-ориентированному проектированию программного обеспечения методами поиска включают в себя: улучшение повторного использования существующих архитектур программного обеспечения через паттерны проектирования, построение иерархической декомпозиции для программной системы, проектирование структуры классов, проектирование архитектуры программного обеспечения на основе спецификаций.

В направлении создания инструментальных средств поддержки проектирования архитектуры программного обеспечения проводят исследования R. Outi [2], S. Mancoridis, B.S. Mitchell и др. [3], Di Penta [4] и др.

Важным этапом эволюционного поиска архитектуры программного обеспечения с улучшенными качествами является задание целевой функции. Часто используются комбиниро- ванные целевые функции, в которых целевое значение складывается из нескольких факторов, каждому из которых задаётся свой вес. В ходе исследования веса могут настраиваться. Сами факторы (например, связность класса, зависимость классов друг от друга) рассчитываются на основе специальных метрик.

Обычно от пользователя требуется составить взвешенную целевую функцию, определяющую, какую архитектуру считать предпочтительнее.

Эволюционное проектирование архитектуры ПС относится к проектированию архитектуры на уровне PIM (Platform Independent Model – Платформо-независимая модель), поэтому характеристиками качества нельзя считать такие параметры, как оценка трудоёмкости выполнения операций, расходование памяти. Можно производить поиск архитектур с лучшими структурными качествами (баланс между максимальной внутренней связностью, минимальной внешней взаимозависимостью и требованием к модульному разбиению проекта).

Если говорить об оптимизации архитектуры систем на основе UML-диаграмм, то при трансформации UML-моделей в процессе поиска неизбежно возникает необходимость проверки корректности модели и семантической эквивалентности её оригиналу. В связи с этим встаёт вопрос о создании средств проверки UML-моделей на корректность и эквивалентность.

• 3.    Теория объектно-ориентированной архитектуры программных систем

• 3.1.    Понятие объектно-ориентированной архитектуры программной системы

Для решения задачи сравнения двух диаграмм классов на предмет семантической эквивалентности автором статьи предложена семантика структуры UML-диаграмм классов. Для описания семантики UML-диаграмм классов формализуются такие понятия из парадигмы объектно-ориентированного проектирования, как архитектура ПС, диаграмма классов, класс, метод и др.

Объектно-ориентированной архитектурой программной системы (ПС) называется архитектура А такая, что

А = {М, RE ST R, F, S , IN, OUT}, где М - UML-модель ПС, RESTR - множество ограничений к ПС, F - множество функциональных требований к ПС, S - семантическое значение ПС, IN - входные данные ПС, OUT - выходные данные ПС.

UML-моделью ПС называется формальная модель М такая, что

М = { D _classes ,D

use

cases , ^D state charts , ^D components , ^D activity , ^D objects} ,

где D _ci_asses - множество диаграмм классов, D _{use cases} - множество диаграмм прецедентов, D _{state c}h_arts - множество диаграмм состояний, D _components - множество диаграмм компонентов, D _acti_vi_ty - множество диаграмм активностей, D _obj_ects - множество диаграмм объектов.

Множество диаграмм классов D classes = { d class O , ...d classm } , где d classi ,i € 0 , ..., т - диаграммы классов.

UML-диаграммой классов dclass называется такая UML-диаграмма, что dclass = {CL, INTR, REL}, где CL - множество классов CL = {classo, ...classk}, INTR - множество интерфейсов INTR = {vn"terfaceo...vn"terfacel}, REL - множество связей REL = {relat‘ionQ...rel^tiang}. Классом class называется такой элемент диаграммы классов Dclassses, что class = {ATR, METH, Р, ST, N}, где ATR - множество атрибутов ATR = {atro...atrn}, METH - множество методов METH = {metho...methm}, Р - класс-родитель (равен null, если родителей нет), ST -признак того, что класс статический (равен 0 или 1), N - идентификатор класса (имя).

Атрибутом называется такой элемент класса attribute, что attribute = {visibility, type, virtual, static, final, name}, где visibility = {public, protected, private} - видимость атрибута, type - тип атрибута, virtual - признак виртуальности, static - признак статичности, final - признак запрета изменения, name - имя атрибута.

Методом называется такой элемент класса или интерфеса method, что method = {visibility, type, virtual, static, fi'nal, name, PAR, LOG_P AR}, где visibility = {public, protected, private} - видимость метода, type - тип возвращаемого значения, virtual - признак виртуальности метода, static - признак статичности метода, final - запрет наследования, name - имя метода, PAR = {par ameter Q...parametern} - множество входных параметров метода, LOG_Р AR = {par ametero...par amet erm} - множество локальных параметром метода, где parameteri = {type, name}, где type - тип параметра, name - имя параметра.

Диаграммой прецедентов duse casei называется такая UML-диаграмма, что duse

case = { AGT, UG, REL } ,

Актор actor, прецедент usecase характеризуются именем. Отношение relation = { name, type, start, end,power } , где name - имя отношения, type - тип отношения, start - начальный участник отношения, end - конечный участник отношения, power - мощность отношения.

Множество диаграмм состояний D state_charts = { d state _chart o , -Estate_cha-rt _m } , где d state_chart _i ,i € 0 , ..., m - диаграммы состояний.

Диаграммой состояний dstate chart называется такая UML-диаграмма, что dstate _chart = {EV, ST, GG, AGT}, где EV - множество событий EV = {evento, ...eventk}, ST - множество состояний ST = {stateo...state/}, GG - множество условий GG = {guard _conditiono...guard_conditiong}, AGT - множество действий AGT = {actiono...actionp}.

Множество диаграмм состояний ^D components — ^{d components o , ...^d components _m ^} , где d _{components i} , i Е 0 ,..., m - диаграммы компонетов.

Диаграммой компонетов dcomponents называется такая UML-диаграмма, что dcomponentsi — {COMP, INTR, REL}, где COMP - множество компонетов COMP — {componento, ...componentк}, INTR -множество интерфейсов INTR — {interfaceo...interface}}, REL - множество связей REL — {relationo...relationg}.

Множество диаграмм активности   Dactivity    —    {dactivityo, -dactivitym}, где dactivityt,г Е 0,..., т - диаграммы активности.

Диаграммой активности называется такая UML-диаграмма dactivity, что dactivity — {ACT, DEC,SP,J}, где ACT - множество действий ACT — {action, ...actionk}, DEC - множество решений DEC — {decisiono...decision[}, SP - множество ветвлений конкурирующих деятельностей SP — {slpito...splitg}, J - множество ветвлений конкурирующих деятельностей J — {joino...joing}.

Множество диаграмм объектов D objects — { d objects o ,...d objects _m } , где d objects i ,i Е 0 ,..., т – диаграммы объектов.

Диаграммой объектов dobjects называется такая UML-диаграмма, что dobjects — {OBJ, INTR, REL}, где OBJ - множество объектов OBJ — {objecto, ...objectk}, INTR - множество интерфейсов INTR —  {interfaceo...interface}}, REL - множество связей

REL — { relation o ...relation g } .

Множество ограничений к ПС RESTR может быть представлено на одном из языков задания спецификаций к UML-модели ПС.

Семантическое значение ПС S может быть выражено в терминах какой-либо формальной семантики UML-диаграмм (аксиоматической, операционной и т.д.).

Входные данные IN - данные, подаваемые на вход ПС для последующей обработки.

Выходные данные OUT - данные, получаемые в результате работы ПС.

• 3.2.    Семантика UML-диаграмм классов

Рассмотрим особенности семантики UML-диаграмм классов.

Под конструктором класса C будем понимать метод C (), вызов которого C.C () приводит к созданию в оперативной памяти объекта класса C .

Вызов конструктора класса возможен лишь у класса C , для которого C.static — false (для нестатических классов).

Под деструктором класса C будем понимать метод ~ C () , вызов которого C. ~ C () приводит к удалению из оперативной памяти объекта класса C .

Вызов деструктора класса возможен лишь у класса C , для которого C.static — false (для нестатических классов).

Выражение C 1 _p i ass ocC2 _p 2 означает, что класс C 1 связан отношением ассоциации мощностью (p l , p 2 ) (см. табл. 1) с классом C 2, где p l , p 2 - количество объектов класса C 1 и C 2 соответственно, участвующих в отношении.

Между классами возможны следующие виды отношений (relations): ассоциация (association), наследование - обобщение (generalization), агрегация (aggregation), композиция (composition), зависимость (dependency).

Между классом и интерфейсом возможно отношение реализации (realization).

Таблица1

Мощность отношений между классами

Мощность отношения	(p1, p2)
один к одному	(1,1)
один ко многим	( 1 , 1 ... n) или ( 1 , 0 ... n)
многие ко многим	( 1 , 1 ... n, 1 , 1 ... n) или ( 0 ... n, 0 ... n)
многие к одному	( 1 , 1 ...n, 1) или ( 0 ...n, 1)

Например, запись С 1 1(— сС2 o ..._n означает, что каждый объект класса С 1 связан отношением ассоциации с 0 ...n объектов класса С 2.

Выражение С1generC2 означает, что класс С1 наследует методы и атрибуты класса С2. Выражение С 1p1aggregC2Р2 означает, что класс С1 связан с классом С2 отношением агрегации.

Аксиома 1. Пусть даны классы  С1

и      С 2

{{ attr l o , attr 1 1 ...attr 1 _n1 } ,

{{ attr 2 o , attr2 1 ...attr2_Tl 2 } ,

{ meth 1 o , meth1 1 ...meth1 _m1 }}

{ meth 2 o , meth 2 1 ...meth 2 _m 2 }} .

Тогда

S [ { С 1 = {{ attr l o , attr 11 ...attr 1 _n1 } , { meth l o , meth 1 1 ...meth 1 _m1 }} , С 2 = {{ attr 2 o , attr 2 1 ...attr 2 _n 2 } , { meth 2 o , meth 2 1 ...meth 2 _m 2 }}} , { ... } , { С 1 gener C 2 ,... } ] = = [ { С 1 = {{ attr 1 o , attr 1 1 ...attr 1 _n1 } U { attr 2 o , attr 2 1 ...attr 2 _n 2 } , { meth 1 o , meth 1 1 ...meth 1 _m1 } U { meth 2 o , meth 2 1 ...meth 2 _m 2 }} , С 2 = {{ attr 2 o , attr 2 1 ...attr 2 _n 2 } , { meth 2 o , meth 2 1 ...meth 2 _m 2 }} , {} , {}} ] .

Аксиома 2. Справедливо следующее выражение:

С 1p1aggregC2Р2 ^ Eatribute G С1 : (type = С2) V (type = Container < С2 >), где type - тип атрибута atribute класса С1, Container < С2 > - контейнер объектов класса С2.

Выражение С 1 _p 1 Comp C 2 _Р 2 означает, что класс С 1 связан с классом С 2 отношением композиции.

Аксиома 3. Справедливо следующее выражение:

(С 1p1CompC2р2) Л (~ С 1()) С2(), где ~ С 1() - вызов деструктора класса С1, ~ С2() - вызов деструктора С2.

Примечание. Аксиома 3 означает, что удаление из оперативной памяти объекта класса С 1 автоматически приводит к удалению из памяти связанного с ним отношением композиции объекта класса С 2. Выражение С 1 depC 2 означает, что класс С 1 связан с классом С 2 отношением зависимости.

Аксиома 4. Справедливо следующее выражение:

С 1depC2 ^ (Emethod G С1) Л ((Eparameter G PAR) V (Eparameter G РОС_PAR)) : type = С2, где PAR - множество формальных параметров метода method, РОС_PAR - множество локальных параметров метода method, type – тип параметра parameter.

Тогда будем считать, что структурная семантика UML-диаграммы классов описывается следующим образом:

S = {{G1 = {{attrli = {{attr1Type, isVirtual, isStatic, isFinal, attr1V ame}}, attr12   =   {...}, ...attr1n =   {...}}, {methG   =   {{type, isVirtual, isStatic, isFinal, name, PAR =      {parameter111      =      {type, name}, parameter 112      =

{      1 1       =        {{ meth 1 ₁        =        {{ type, isVirtual, isStatic, isFinal, name,

PAR =    { parameter 1 1 1     =    { type,name } , parameter1 _{1 2}    =    { type, name } ...

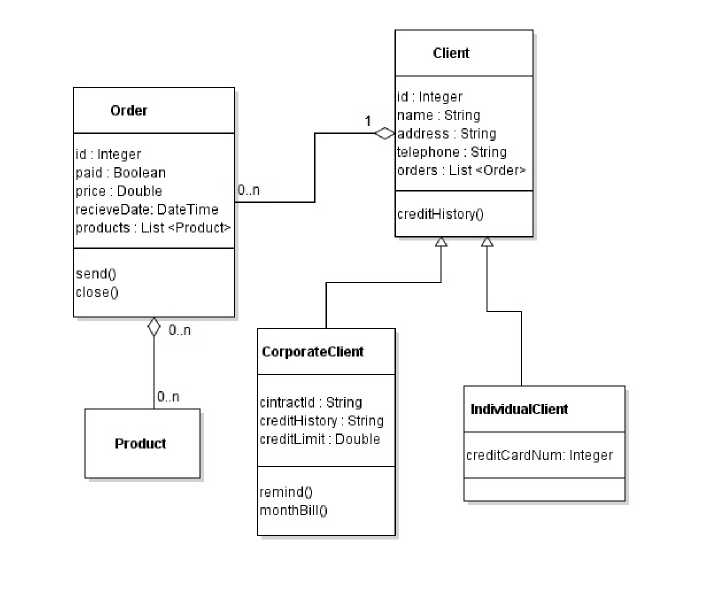
Рис. 2. Пример диаграммы классов

Например, семантическое значение диаграммы классов на рис. 2 будет следующим: S = {{ G 1 = {{ atr 1 ₁ = {{ Integer, false, false, false, „ id „ }} , atr 1 ₂ = {{ String, false, false, false, „ name,, }} , atr 1 3 = {{

String, false, false, false, „address,,}}, atr14 = {{String, false, false, false, „telephone,,}}, atr15 = {{List < Order >, false, false, false, „orders,,}}},

{ meth 1 ₁ = { void, false, false, false, „cr^diGdistary,, PAR = {} ,

LOG_PAR = {}} , false, „Client,},

G2 = {{{atr11 = {{Integer, false, false, false, „id„}}, atr22 = {{Boolean, false, false, false, „paid„}}, atr23 = {{Double, false, false, false, „price„}}, atr24 = {{DateTime, false, false, false, „recieveDate„}}, atr25 = {{List < Product >, false, false, false, „products„}}}, { meth21 = {void, false, false, false, „send„, PAR = {}, LOG_PAR = {}}, meth22 = {void, false, false, false, „cloee„, PAR = {},

LOG_PAR = {}}} , false, „ Order „ } ,

G3 = {{atr31 = {{String, false, false, false, „coatractld”}}, atr32 = {{String, false, false, false, „creditHistory„}}, atr33 = {{Doable, false, false, false, „creditLimit„}}}, { meth31 = {void, false, false, false, „remind,,, PAR = {}, LOG_PAR = {}}, meth32 = {void, false, false, false, „monthBill,,, PAR = {},

LOG _PAR = {}}} , false, „ GorporateGlient „ } ,

G 4 = {{ atr4 1 = {{ Integer, false, false, false, „ creditGardNum „ }}} , {} , false, „IndividualGlient,, } ,

G 5 = {{} , {} , false, „Product,}}, {} , { G 1 1 - ggreg G 2 o ..n ,

G 2o. ._n aggre g C 5 o ..n , G3g e n er G 1 , G4 gener G 1 }}

Выражение G 1 rea{ 1 1 означает, что класс G 1 связан с интерфейсом 1 1 отношением реализации (реализует методы интерфейса 1 1 ), причём множество методов класса G 1 M q 1 содержит в себе множество методов интерфейса 1 1 М / 1 :

M i 1 С М _С 1 .

• 3.3.    Семантически эквивалентные трансформации UML-диаграмм классов

Под трансформацией UML-диаграммы будем понимать такое изменение структурных элементов UML-диаграммы, которое обеспечивает инвариантность ее семантического значения S.

Теорема 1. (Следствие из Аксиомы 1) – Первая эквивалентная трансформация. Пусть в UML-диаграмме классов dclasses дан класс-родитель G 1 = {{ attr 1 1 , attr1 2 , ...attr 1 _n } , { meth 1 1 , meth 1 2 , ...meth 1 _m } ... } и даны классы G 2 = {{ attr 2 j } , { meth2 j } ... } ...GN = {{ attrN i } , { methN j } ... } . Причем G 2 ...GNgenerG 1 . Тогда

S [ d _c/_asses ] = S [ { G 1 = {{ attr 1 1 , attr1 ₂ , ...attr 1 _n } , { meth 1 1 , meth 1 ₂ , ...meth 1 _m } ... } ,

G 2 = {{{{ attr 1 1 , attr 1 ₂ , ...attr 1 _n } U { attr 2 j }} , {{ meth 1 1 , meth 1 ₂ , ...meth 1 _m } U

U{meth2j}},...}, G3 = {{{{attr11, attr12, ...attr1n} U {attr3j}}, ...{{meth11, meth12, ...meth1m} U {meth3j}},...}, ...GN = {{{{attr11, attr12,... attr1n} U {attrNj}}, {{meth11, meth12, ...meth1m}U {methNj}},...}}, {}, {}}], где attr2j, attr3i, ... attrNi - атрибуты классов C2 ... CN, meth2j, meth3j, ... , methNj -методы классов G2 ... CN.

Доказательство.

G 3generG 1...GNgenerG 1 }} . -------->              -------->

Поочерёдно заменяя по Аксиоме 1 класс Gi =    {{attrij}, {methi^}...} и отношение наследования     GigenerG 1     в левой части на

Gi = {{ attri j } U { attr 1 1 , attr 1 ₂ , ...attr 1 _n } , { methi k U { meth 1 1 , meth1 ₂ , ...meth 1 _m }} ... } , получаем

S [ d _c/_asses ] = S [ {{ G 1 = {{ attr 1 1 , attr 1 ₂ , ...attr 1 _n } , { meth 1 1 , meth1 ₂ , ...meth 1 _m } ... } ,

G 2 = {{ attr 1 1 , attr 1 ₂ , ...attr 1 _n }U{ attr 2 j }} , {{ meth 1 1 , meth 1 ₂ , ...meth 1 _m }U{ meth 2 j }} ,... } ,

G 3 = {{ attr 1 1 , attr 1 ₂ , ...attr 1 _n }U{ attr 3 j }} , {{ meth 1 1 , meth 1 ₂ , ...meth 1 _m }U{ meth 3 j }} ,... } ,...

U{ methN ₃ }} ,... }} , {} , {}} ] .

Что и требовалось доказать.

Аксиома 5 (Вторая эквивалентная трансформация) – Интерфейс. Справедливо следующее соотношение:

S [ {{ C 1 , С 2 } , { I 1 } , { С 2 p i - epI 1 _Р 2 , С1 r_ e^ I 1 }} ] = S [ {{ С 1 , С 2 } , {0} , { С2 р і - ерС 1 p 2 }} ] .

Рассмотрим в качестве примера семантически эквивалентной трансформации UML-диаграммы классов шаблон проектирования Фасад, предложенный Гаммой [1].

Аксиома 6 (Третья эквивалентная трансформация) – Фасад (Facade). Справедливо следующее соотношение:

S[{{С 1, С2..СН}, {...}, {... U {CКdep{C2 V С3 V .. V СН}... СМ dep{C2 VC3 V .. VCN}}}] =

= S[{{С 1 = {{{attr1j} U {С2..СН}}, {{meth1i} U {{meth2j} U {meth3k} U U{met^N/}}}}, {...}, {... U {CК...CМdepC 1}}], где С1 — класс-обёртка (фасад) для остальных классов СС2 ... CN, attr1i - атрибуты класса С1, metMi — методы класса С1, {meth2j} U {met^3^} U ... U {methNf} - мето-ды,соответствующие вызову соответствующих методов, принадлежащих классам С2 ... СН с параметром visibility = public, СК ... СМ - классы, связанные с классами С2 ... CN отношением зависимости (dependency).

• 4.    Заключение

В работе рассматриваются вопросы эволюционного проектирования объектноориентированной архитектуры программного обеспечения.

Приведено формальное описание таких понятий из объектно-ориентированной парадигмы проектирования, как архитектура ПС, диаграмма классов, диаграмма прецедентов, класс, интерфейс, метод, отношение наследования и т.д.

Предложен формальный аппарат для описания семантики UML-диаграмм классов, позволяющий ввести понятие семантически эквивалентной трансформации диаграммы классов. Данный аппарат необходим для реализации эволюционного проектирования архитектуры программного обеспечения (в частности – поиска диаграммы классов с улучшенными структурными свойствами, семантически эквивалентной исходной).

Так же в работе на основе разработанного формального аппарата описываются семантически эквивалентные трансформации (наследование, введение интерфейса, введение предложенного Гаммой паттерна проектирования Фасад (Facade)).

По теме статьи автором будет сделан доклад на предстоящей II Международной научной конференции «Инжиниринг и телекоммуникации» Москва, 18–19 ноября 2015 года.