Семейство кривошипно-коромысловых механизмов с максимумом угла передачи при угле поворота кривошипа, равном 300

Кинематические схемы многих технологиче- ских машин содержат кривошипно-коромыс-ловые механизмы (ККМ). Применительно к линиям пищевых производств приведем примеры технологических машин, кинематические схемы которых включают названный механизм: устройства для передачи изделий [1], укладочные машины [2], тестомесильные машины [3, с. 34]. Известны графоаналитические методы синтеза ККМ [4, 5, с. 238–248; 3, с. 75–84]. Эти методы позволяют проектировать названный механизм по исходным данным: по заданному ходу и углу качания коромысла; по коэффициенту увеличе-ния средней скорости коромысла при этом вводится дополнительное условие – угол передачи не опускается ниже минимально допустимых его значений; по заданным двум или трем положениям ведущего и ведомого звеньев. Графоаналитические методы синтеза ККМ не дают информации о характере изменения функции угла передачи этих механизмов в периоде кинематического цикла.

Известен метод синтеза ККМ, позволяющий определять геометрические параметры, используя область существования этих механизмов и расчетные формулы. Область существования геометрически проворачивающихся ККМ предложена Н.И. Колчиным [6, стр. 86]. Математическая модель названной области описывается тремя равенствами

1 - λ1 = λ2 - λ31 - λ1 = λ3 - λ21 + λ1 = λ2 + λ3,

В первой четверти прямоугольной системы координат с осями λ ₂ и λ 3 математическая модель, описываемая равенствами (1) – (3), представляет собой три прямые линии. В той же системе координат условие геометрической проворачиваемости с учетом углов передачи ККМ – два эллипса [6].

Известен метод синтеза ККМ, позволяющий согласовать характер изменения функции угла передачи в периоде кинематического цикла с характером изменения технологической нагрузки, приложенной к механизму [7]. Этот метод основан на делении ККМ на семейства по признаку: положению механизма, в котором наблюдается максимум функции угла передачи, равный 90о. Так, максимум функции угла передачи семейств ККМ наблюдается в наиболее характерных положениях:

• 1)    продольная ось кривошипа перпендикулярна линии центров (ККМ-1);

• 2)    продольная ось кривошипа – продолжение линии центров (ККМ-2);

• 3)    продольная ось кривошипа лежит на линии центров (ККМ-3);

• 4)    продольная ось шатуна наложена на кривошип; 5) продольные оси кривошипа и шатуна вытянуты в одну линию (ККМ-5);

• 6)    продольные оси кривошипа и коромысла параллельны, при этом названные звенья лежат по одну сторону от линии центров (ККМ-6);

• 7)    продольные оси кривошипа и коромысла параллельны, при этом упомянутые звенья лежат по разные стороны от линии центров (ККМ-7).

В развитие метода синтеза, учитывающего характер изменения функции угла передачи ККМ, выделим еще одно семейство таких механизмов. Для этого семейства механизмов характерно, что максимум угла передачи, равный 90о, наблюдается в положении КММ при ф = 30°, где ф - угол поворота кривошипа. Отсчет угла ϕ принят от положения, при котором кривошип лежит на линии центров в направлении против часовой стрелки. Обозначим условно это семейство кривошипно-коромысловых механизмов – ККМ-30о. На рис. 1 представлен ККМ в положениях, когда функция угла передачи максимальна µmax = 90о и мини- мальна µmin . Обозначим l1, l2 и l3 – длины кривошипа, шатуна и коромысла соответственно; l0 – длина межцентрового расстояния.

Из произвольного треугольника AOO 1 для q = AO 1 имеем

• 11    +10 - 2 ■ 1, ■ 10 ■ cos(30*) = q2

  
  
  

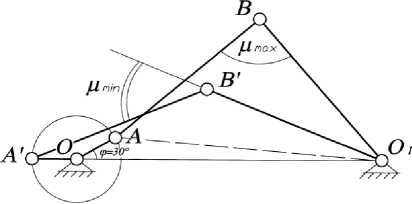
Рис. 1. ККМ в положениях, когда угол передачи максимален и минимален

Из прямоугольного треугольника ABO 1 для q получим 22  2

• l 2    + l 3 = q .                (5)

Совместно решим (4) и (5)

X2+X3 = X1 ■ (X1 - 73;+1

,

где X =   , Л ₂ = l²

l0            l0

и X2 = — - относительные длины l0

кривошипа, шатуна и коромысла соответственно.

В первой четверти прямоугольной системы координат с осями X2 и Х3 математическая модель (6) - дуга окружности произвольного радиуса

R = VX • (X - D) +1, при этом центр дуг окружностей – в начале системы координат. Выразим из 1 + X = X + X длины X2 и хз , подставим их в (6) и получим два уравнения

X

— X 3 • ( X 1 + 1) + X •

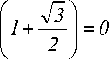
X2 - Х2 • (Х1 + 1) + Х1 •

У 2 7

= 0

Корни уравнений (7) и (8) равны

X 1 + 1  у/^{X — 2} • ^X • ⁽1 + 33 ) + ¹

X =± 3 _{2                2}

;

x + 1 , V ^{X - 2} • х ■ ⁽1 ⁺ х) + ^{+ 1}

X =---±----------------

2 _{2               2}

Из (9) и (10) видно, что эти уравнения имеют один корень, если х2 - 2 • х1 • (1+4з)+1=о

.

При этом X 1 = 0,1896 ; X ₂ = Х ₃ = 0,5948 . Следовательно, относительную длину кривошипа семейства ККМ-30^о можно варьировать в пределах от 0 до 0,1896.

Таблица 1. Координаты точек пересечения математической модели ККМ-30^о с прямой Н.И. Колчина

Длина X 1	Длина X 2	Длина Х 3
0,05	0,9520 0,0980	0,0980 0,9520
0,10	0,8904 0,2096	0,2096 0,8904
0,15	0,8002 0,3498	0,3498 0,8002
0,1896	0,5948	0,5948

Получим координаты точек пересечения математической модели (6) ККМ-30о с прямой (3) Н.И. Колчина (см. табл. 1).

По координатам, приведенным в табл. 1, построена область существования ККМ-30^о. Область существования ККМ-30^о, определяющая условия геометрической проворачиваемости этого семейства механизмов, представлена на рис. 2. Эта область – сочетание дуги abc окружности единичного радиуса R = 1 (при X 1 = 0 ) и кривой cda , полученной путем пересечения дуг окружностей произвольного радиуса R = V X • ( X - 31 ) + 1 (при 0 < X 1 <  0,1896 ) с прямой (3) Н.И. Колчина.

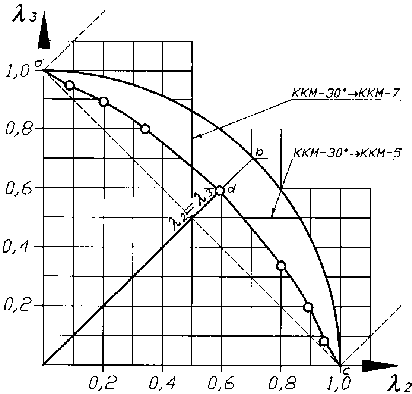
Рис. 2. Область существования семейства ККМ-30^о

Точки, лежащие на кривой cda , соответствуют ККМ-30˚ с минимальным углом передачи, равным 0^о. При этом якобиан исходной системы двух уравнений анализа ККМ равен нулю. Таким образом, точки, принадлежащие кривой cda , соответствуют ККМ-30^о, имеющим в периоде кинематического цикла особое (мертвое) положение. Точки на дуге abc соответствуют механизмам с параметром X 1 = 0 . Механизмы семейства ККМ-30^о вне области abcd не существуют. Совместный анализ математической модели ККМ-30^о и математических моделей известных [7] механизмов ККМ-5 и ККМ-7 позволил установить:

• 1)    при Х ₃ = 0,5 = const , х + X = у- математическая модель ККМ-30^о соответствует ККМ-5. В этом случае максимум функции угла передачи наблюдается в двух положениях названного механизма: при ф = 30 ° , что соответствует положению, когда продольные оси кривошипа и шатуна вытянуты в одну линию (ККМ-5) и при ф = 330 ° ;

• 2)    при Х ₂ = 0,5 = const , X + X = математиче

ская модель ККМ-30^о соответствует ККМ-7. В этом случае максимум функции угла передачи наблюдается в двух положениях названного механизма: при ф = 30 ° и при ф = 330 ° , что соотносится с положением, когда продольные оси кривошипа и коромысла параллельны, причем кривошип и коромысло лежат по разные стороны от линии центров (ККМ-7).

Приведем примеры практического применения области существования ККМ-30о (рис. 2).

• 1.    Выбираем в области по рис. 2 точку, устанавливаем ее координаты: A = 0,70 и A ₃ = 0,60 . По (6) рассчитываем относительную длину кривошипа A = 0,09 . Задаемся длиной межцентрового расстояния и определяем размеры звеньев ККМ-30^о в миллиметрах.

• 2.    Пусть A = 0,146 . Примем A 2 = A 3 . По (6) имеем, что A 2 = A 3 = 0,620 . Конструктивно выбираем

длину кривошипа и устанавливаем размеры звеньев ККМ-30˚ в миллиметрах. Силовая работоспособность ККМ оценивается функцией угла передачи, которая изменяется в периоде кинематического цикла в зависимости от значений длин звеньев. Для выделенного семейства ККМ-30о получим зависимости для угла передачи. Из рис. 1 видно, что угол передачи семейства ККМ-30о в функции угла поворота кривошипа ф со- ставит

(

^A i •

A i

= arccos

^cos( фi ⁾ — у

A • A v 7. (12)

По зависимости (12) установлен характер изменения функции угла передачи семейства ККМ-30о. Функция угла передачи этого семейства механизмов сохраняет значения, близкие к 90о, на одной трети интервала рабочего хода и к концу рабочего хода снижается, не достигая минимума. Минимум функции угла передачи наблюдается в положении механизма, когда продольная ось кривошипа – продолжение линии цен- тров, то есть при фt =180о. Представим минимальный угол передачи ККМ-30о в функции трех аргументов – относительных длин Ai, A2 и Аз

A

( Г

A i • 1

^A min

= arccos

^A 2

+ —

• А з

^{v               7} .                    (13)

При условии, что длины A2 = A3, минимальный угол передачи составит

2 • A i • 1 + —

A min = arccos

^{V                 7} .              (14)

Анализ выражения (14) показал, что с увеличе- нием длины Ai значения угла Amin уменьшаются, при Ai = 0,1896 угол Amin = 0о. Для решения практических задач проектирования ККМ-30о получим зависимости для минимального угла передачи в функции двух аргументов ^min = f( Ai, A3) и Amin = Ф( Ai,A2> соответственно

A i •

i + —

л

A min = arccos

^A 3 ■ д/ ^A i ■ ^(A i ^- V ³) ^{- A} 2 ^{+ i}

V                                7.

;

^A i •

i + —

A

A min = ^arccos

A 2 • V A _i • ( A _i - V 3) - A 2 + 1

^{V                               7} .     (16)

На рис. 3 приведены графики угла передачи

A min , полученные по зависимости (16).

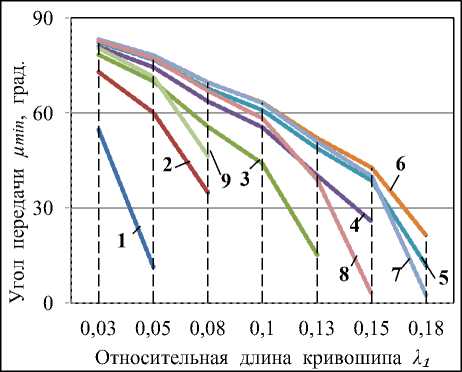
Рис. 3. Минимальный угол передачи в функции

^A i при ^A 2 = const:

1 - A ₂ = 0,i0 ; 2 - A ₂ = 0,20 ; 3 - A = 0,30 ; 4 - A ₂ = 0,40 ; 5 - A 2 = 0,50 ; 6 - A 2 = 0,60 ; 7 - A ₂ = 0,70 ; 8 - A ₂ = 0,80 ; 9 - A ₂ = 0,90

Из выражений (15) и (16) следует, что влияние длин ^A 2 и A 3 на угол передачи A min симметрично. Анализ графической интерпретации на рис. 3 позволил заключить: 1) с увеличением длины ^A _i при у = const угол A mtn уменьшается; 2) с повышением A 2 при A _i = const угол ^A min увеличивается до определенного значения, а затем снижается (при больших значениях A 2 ).

Приведем примеры практического применения зависимостей (13) – (16) и графической интерпретации (рис. 3) для семейства ККМ-30о.

• 1.    Определить значение минимального угла передачи для семейства ККМ-30^о, если известны относительные длины звеньев: A = 0,70 и A = 0,09 . По зависимости (16) получим, что A min = ⁶⁶ ° ² . Аналогичный результат можно получить по кривой 7, приведенной на рис. 3.

• 2.    Спроектировать ККМ-30^о, в котором при относительной длине шатуна A = 0,90 минимальный угол передачи должен быть не меньше 40^о. На рис. 3 выбираем кривую 9, эта кривая построена при A = 0,90 . Видим, что условие Ai_п - 40 ° выполняется при A = 0,08 . По зависимости (6) определяем относительную длину коромысла. Имеем A ₃ = 0,24 . Зная длины ^A _i , ^A 2 и ^A 3 , по зависимости (13) уточняем фактическое значение минимального угла передачи. Угол передачи A _min = 46 ° i6 , что удовлетворяет условию числового примера.

Выводы: в результате теоретических исследований для семейства ККМ-30^о установлены следующие закономерности:

• 1.    Область существования ККМ-30^о, определяющая условия геометрической проворачиваемости этого семейства механизмов – сочетание дуги окружности единичного радиуса R=1 (при Я , = 0 ) и кривой, полученной путем пересечения дуг окружностей произвольного радиуса R = ^ Я • ( Я — 3) + ¹ (при 0 < Я - 0,1896 ) с прямой (3) Н.И. Колчина.

• 2.    ККМ-30^о, геометрические параметры которых принадлежат кривой, полученной путем пересечения дуг окружностей произвольного радиуса R = V Я , • ( Я , - 33 ) + 1 (при 0 < Я - 0,1896 ) с известной прямой Н.И. Колчина – это семейства механизмов ККМ-30^о с минимальным углом передачи, равным 0^о.

• 3.    Области соответствия математической модели (6) семейства ККМ-30^о моделям известных семейств ККМ-5 и ККМ-7 – прямые линии, параллельные оси абсцисс Я и оси ординат Я соответственно.

• 4.    Минимальный угол передачи семейства ККМ-30^о с увеличением относительной длины кривошипа Я при постоянной длине шатуна Я 2 (или длине коромысла Я 3 ) уменьшается; при постоянном значении относительной длины Я 1 с увеличением длины Я 2 (или Я ₃ ) этот угол повышается до определенного значения, а затем снижается.

• 5.    В практическом плане семейство ККМ-30^о более предпочтительно для применения в составе машин с возвратно-поворотным движением рабочего органа, технологическая нагрузка которых изменяется в интервале рабочего хода по комбинированному закону, сочетающему приближенно постоянный характер изменения нагрузки в начале (на одной трети интервала) рабочего хода и уменьшающийся к концу интервала рабочего хода.