Семейство точных решений уравнений Навье-Стокса для верификации компьютерных программ

Решением уравнений Навье-Стокса. называют пару полей: поле давления и поле скорости, удовлетворяющие этим уравнениям. Говорят, что поле скорости удовлетворяет уравнениям Навье-Стокса, если существует поле давления, составляющее вместе с этой скоростью решение уравнений Навье-Стокса. При заданном поле внешних сил не для всякого поля скорости можно «подобрать» соответствующее поле давления. Поэтому не всякое поле скорости является решением уравнений Навье-Стокса.

Ниже, для краткости, будем иногда, опускать слово поле перед словами давление и скорости, понимая при этом, что речь идет о полях давления и скорости.

Если поле внешних сил потенциально, то сумма Vi + V2 скоростей, удовлетворяющих уравнениям Навье-Стокса, будет скоростью некоторого решения уравнений Навье-Стокса,

«Московский физико-технический институт (национальный исследовательский университет)», 2020

если и только если поле вектора V1 xrot V2 + V2 xrot V1 является градиентом скалярного поля. Это условие выполнено, например, для семейства винтовых (П = rot V = AV = 0, где A = const) течений, в которое входят все винтовые течения с одинаковым коэффициентом A. Наиболее известными стационарными винтовыми течениями идеальной жидкости являются течения Громеки-Бельтрами [1-2] и ABC-течение [3]. Любая винтовая скорость удовлетворяет уравнениям Эйлера - соответствующее поле давления существует. Но в общем случае эта скорость не удовлетворяет уравнениям Навье-Стокса (невозможно «подобрать» поле давления). Однако, как показал в 1919 году В. Тркал [4], скорость винтового течения, умноженная на exp( — at) , г де t — время, будет удовлетворять уравнениям Навье-Стокса при надлежащем выборе параметра а. Такая возможность получать точные нестационарные решения уравнений Навье-Стокса из стационарных решений уравнений Эйлера имеет место для всех винтовых течений [4]. В качестве решений, допускающих сложение скоростей, исследовались и такие решения, в которых П = AV, а коэффициент A может зависеть от координат и времени [4-5]. При этом решения, для которых поле вектора V 1 x гоt V2 + V2 x гоt V1 не равно нулю, но сложение скоростей возможно (поскольку это поле является градиентом некоторого скалярного поля), не были известны. Если говорить точнее, то не были известны решения, которые после сложения скоростей дают новое решение с другой картиной течения (например, новую картину линий тока, не совпадающую с картинами линий тока исходных решений). При этом решения, дающие после сложения те же линии тока, были известны. Например, к известным решениям, для которых поле вектора V 1 x гоt V2 + V2 x гоt V1 является ненулевым градиентом скалярного поля, относятся решения Куэтта [6] и Пуазейля [7]. Но в результате сложения скоростей различных решений Куэтта получается «новое» решение Куэтта с теми же линиями тока. Аналогичная ситуация имеет место и для решений Пуазейля. Поэтому следует уточнить, что до сих пор известно очень мало решений с различными картинами линий тока, допускающие сложение скоростей при ненулевом поле вектора V 1 x гоtV2 + V2 x гоtV1. Во всяком случае, такие решения не упоминаются в работах [4, 5, 8]. Не упоминаются они ни в классических учебниках [9-10], ни в монографиях [11-14], ни в обзорах [15-17]. Нет таких решений и среди результатов [18-22], полученных после опубликования обзоров [15-17]. Заметим, что решения [22] допускают сложение скоростей, но эти решения винтовые, и в них вектор V 1 x гоtV2 + V2 x гоtV1 равен нулю. Автору данной статьи удалось найти лишь два примера. Это цилиндрические (радиальная скорость равна нулю) решения [23] и некоторые из плоских решений [24].

В данной работе представлено семейство осесимметричных невинтовых ( V x rot V = 0) точных решений уравнений Навье-Стокса (в отличие от [23] радиальная скорость найденных решений отлична от нуля), скорости которых можно складывать, получая в итоге скорость некоторого другого решения уравнений Навье-Стокса, входящего в представленное семейство. Это свойство скоростей названо линейностью по скорости. Само семейство названо П/г-семейством, поскольку во всех его решениях отношение завихренности к радиусу постоянно по пространству.

Другие заслуживающие внимания свойства решений П/г-семейства представлены в седьмом разделе данной работы.

2.    Уравнения движения

Рассмотрим осесимметричное течение вязкой несжимаемой жидкости в потенциальном поле массовых сил. Далее будут использоваться следующие безразмерные переменные: V — скорость; П = rotV — завихренность; р — давление, отнесеиное к плотности; П — потенциал объемных сил; Re — число Рейнольдса, t — время. Движение жидкости описывается уравнениями Навье-Стокса в форме Громеки-Ламба [9-10]. С учетом равенства AV = —гоt П, верного для несжимаемой жидкости, их можно представить в виде

Э              1       „

[р    ' + П],

—V + П x V =--rot П — V dt              Re divV = 0. (2)

Введем цилиндрическую систему координат г, е, z с началом в точке О так, чтобы ось Oz совпала с осью симметрии течения. Параметры осесимметричного течения не зависят от окружной координаты е. Пусть е_т, е_е, е_г — правая тройка единичных векторов в радиальном, окружном и осевом направлениях соответственно. Вектор скорости имеет вид V = V_Te_T + Р^е_е + V_ze_z, а функции V-, V_e, V_z,р и П зависят только от переменных г, z и t. Ниже будем отождествлять скорость и набор функций V_T,V_e,V_z. В частности, будем говорить, что функции V ,V_e,V_z являются решением уравнений Навье-Стокса, если скорость V = Ү_те_т + V _ee_e + V _ze_z удовлетворяет уравнениям (1), (2).

3.    Основное точное решение

Для произвольной константы А рассмотрим стационарные поля скорости V = Ке_т + V_ee_e + V_ze_z и давления:

V t = Arz, V = 0, V =

—Az2,

Р = Ро — 2^Az Re

—

A2 z4

— П,

где константа ро > 0 обеспечивает положительность давления в рассматриваемой ограни-

ченной области. Покажем, что эти поля удовлетворяют уравнениям Навье-Стокса. В цилиндрических координатах, с учетом независимости параметров течения от окружной координаты е. уравнение неразрывігости (2) упрощается: TdT ( rV ) + d; Vz = 0. Подстановка выражений (3) превращает последнее уравнение в тождество. Поэтому поле (3) соленои-дально - удовлетворяет уравнению неразрывности (2).

Завихренность поля скорости, вычисленная в цилиндрических координатах, равна

Q = (—дУЬ+(д^

—

^V?) е_£ + f¹ 1- (rV_e)) е_г = Аге_е. ог )     \тот /

Отсюда получаем векторное произведение Q xV = (—A2rz²) е_т+ (—A2r²z) е_г = V (

—

аму)

входящее в левую часть (1). Вязкое слагаемое уравнений Навье-Стокса представляется в виде ^г ot Q = 0 • е_т + 0 • е_е + Це_г = V (Цz). Поэтому проверка уравнения (1) сводится к проверке равенства V ——X2^T2^2'^ = —V (Цz) — V рр + ^- + П|, которое выполнено в силу (3)и(4).

Итак, функции (3) и (4) представляют собой точное решение уравнений Навье-Стокса. Будем называть его основным точным решением. Поскольку V и V_z можно представить

в виде V_T

1 d A ² r ² ^ ² тЭг 2      , ^ ^

Т dT (—2— b линии тока основного решения лежат на

гиперболах rz = const. В этом решении можио рассмотреть две 'зоны z < 0 1i z > 0. В каждой зоне основное решение описывает взаимодействие струи со сложным профилем скорости со стенкой, расположенной в плоскости z = 0. Течения по разные стороны от плоскости z = 0 не симметричны относительно этой плоскости. Но для обоих течений скорость (3) на плоскости z = 0 равна нулю (рис. 1).

Поэтому по обе стороны от плоскости z = 0 решение (3) и (4) дает решение двух разных задач. В каждой задаче струя взаимодействует со стенкой, на которой выполнено условие прилипания. Но в одной задаче (справа) струя направлена к стенке, а в другой (слева) -от стенки. Условия на поверхностях, выбранных в качестве остальной части границы, для этих задач можно взять из самого решения (3) и (4).

На плоскости z = 0 давление постоянно и жидкость покоится. Но этого недостаточно для рассмотрения задачи о течении вязкой жидкости со свободной поверхностью. Дело в том, что тангенциальная составляющая завихренности на свободной поверхности вязкой жидкости должна быть равна нулю. Однако для решения (3) и (4) это не так.

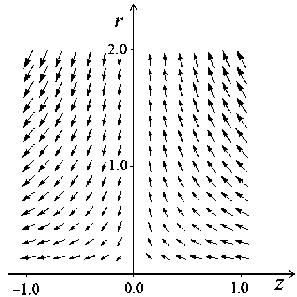
Рис. 1. Поле скорости основного решения. Размер стрелок пропорциопалеп величине скорости

В случае невязкой жидкости требование о равенстве нулю тангенциальной составляющей завихренности может быть снято. Несложно проверить, что если положить р = ро — ^-2^- — П (случай Re = то), то в каждой из зон г < 0 и г > 0 скорость (3) будет решением задачи со свободной поверхностью для уравнений Эйлера.

Основное точное решение представляет собой однопараметрическое (параметр А) семейство решений. Но различные решения могут быть получены не только выбором различных значений параметра А. «Сдвинутое» вдоль оси симметрии решение останется решением уравнений Навье-Стокса (1), (2). То есть для произвольной константы го функции

V_r = ^Ат (^г — ^го),^Ң = 0, У, = ^—А (^г — ^го) ,                        (6)

2А            А2 (г — го)4

р = ро ^{— (г — г}0) --2--^П(т, ^г)                          ( - )

также будут решением уравнений Навье-Стокса. Скорость (3) отличается от скорости (6) на вектор b = Атгое _т + (—2Агго + Аг2) е_г. Поле этого соленоидального вектора потенциально. То есть скорость точного решения (6), (7) получается сложением скорости основного решения и скорости b некоторого потенциального течения несжимаемой жидкости. Оказывается, что вектор b в этом смысле не уникален. Это будет показано в следующем разделе.

4.    Добавление скорости нестационарного потенциального течения

Для любого гладкого осесимметричного потенциального соленоидального поля вида

U = U_r(т, г, t ) е_т + ( А/т ) е_е + U_z ( т, г, t) e_z ,                         (8)

где А = const, существуют функция тока ф = ф(т, г,t) и потенциал радиально-осевой скорости у = у(т, г,t) такие, что U = ¹ ^ф, U = — ¹ д^ф, U_T = д^у, U = д^у.

Обозначим: V* = Ү* ( А, т, г ) и р* = р* ( А, т, г) — основное решение (3), (4). И пусть (8) — гладкое потенциальное соленоидальное векторное поле, а ф = ф(т, г,t) и у = у(т, г,t ) — функция тока и потенциал, соответствующие функциям U_T и U_z. Покажем, что сумма скоростей V* + U является скоростью некоторого решения уравнений Навье-Стокса. Поскольку скорости V* и U соленоидальны, то для этого достаточно показать, что существует такое поле давления р, что выполняется уравнение (1). Найдем такое поле давления.

Векторное произведение, входящее в левую часть (1), записывается в виде rot (V * + U)x(V * +U) = rotV*x Ү*+ Ате _exU = rotV* xV * + ( — А £ф) e_r+ ( — А дф) е_г = = гоt V* x V * + V ( —Аф). Добавление потенциальной скорости U не меняет вязкое слагаемое уравнений Навье-Стокса ^rotrot (V* +U) = V (2^г). Таким образом, давление р нужно подобрать так, чтобы выполнялось равенство

V (д|у) + _rot V* x V* + V (— Аф ) = —V (|Аг) —

(V * +и) ²

^V р ⁺ "—2--

+ П .     (9)

Но V* - решение уравнения rot V* х V* = —V (2^г) — V рр* + (V2) + П|. Поэтому (9) будет выполнено, если положить р=р+А«—^+(?—'+'■

Искомое поле давления найдено. Следовательно, скорость V* +U является скоростью некоторого решения уравнений Навье-Стокса.

Заметим, что, согласно (5), отношение завихренности основного решения к расстоянию г до оси симметрии постоянно и равно А. Поскольку ротор потенциального поля U равен нулю, это отношение останется равным А и для решения V* + U.

Определение. Множество всех точных решений уравнений Навье-Стокса, у которых скорость представляется в виде суммы скорости основного решения (3), взятого при каком-либо значении параметра А, и скор ости U = U (г, г, t) некоторого потенциального течения несжимаемой жидкости вида (8), будем называть П/г-семейством решений. Такое название представляется естественным, поскольку в этом семействе отношение завихренности к радиусу постоянно во всем течении.

Несложно проверить, что решения Пуазейля входят в П/г-семейство. Поэтому можно считать П/г-семейство решений обобщением решений Пуазейля.

Замечание. Для течений, в которых жидкость достигает оси симметрии, необходимо рассматривать только такие решения П/г-семейства, в которых А = 0.

5.    Линейность по скорости

Пусть V* (А1,г, г) + Ui (г, г, t) ii V* (А2,г, г) + U2 (г, г, t)   — два по ля скорости из П/г-семейства решений. Их линейная комбинация равна ki {V* (Ai, г, г) + Ui (г, г, t)} + ^2 {V* (А2, г, г) + U2 (г, г, t)} = V* ((kiAi + ^2А2), г, г) + + kiUi (г,г, t) + k2U2 (г,г, t), то есть представляется суммой скорости основного решения у * = у* (А, г, г), взятого при значении параметра А = kiAi + k2A2, и некоторой соленоидальной потенциальной скорости вида (8). Следовательно, линейная комбинация скоростей принадлежит П/г-семейству решений уравыеішй Навье-Стокса. То сеть П/г-ееменетво является линейным по скорости.

6.    Построение примеров точных решений для верификации численных алгоритмов

Следует заметить, что решения П/г-семейства соответствуют течениям, которые трудно реализовать в эксперименте или наблюдать в реальной обстановке. Это связано со сложностью создания граничных условий (которые должны быть взяты из самих решений). Но если речь идет о верификации, то есть о проверке точности численного алгоритма, не обязательно иметь техническую возможность реализовать краевые условия в эксперименте. Большинство численных алгоритмов работают с любыми граничными условиями. При этом верификация требует наличия точных выражений для функций U_r , U_z и для соответствующих им функций тока ^ и потенциалов р. Основой для построения таких точных решений может служить набор частных решений уравнения Лапласа (для потенциала р), записанного в цилиндрической системе координат, и полученных «стандартным» методом разделения переменных. Такие решения можно найти в разделе 8.1.2-1 справочника [25]. Однако в выражение для давления (10) входит функция тока, не представленная в упомянутом справочнике. Нахождение этой функции по известному потенциалу является несложной задачей. Тем не менее (для удобства использования данной работы в целях верификации численных алгоритмов) приведем некоторые линейно независимые варианты осесимметричной соленоидальной и потенциальной скорости U = U _re_r + 0 • е_е + U _ze_z, а также соответствующие этим вариантам функции тока ^ и потенциалы р.

• 1.      U_T = p J_i(pr) exp(pz), U _z = — p Jo(pr) exp(pz),

• 2.    U_r = —pJ_i(pr) exp(— pz), U_z = —pJ₀(pr) exp(—pz),

• 3.       U_T = pI_i(pr) cos(pz), U_z = — plo(pr) sin(pz),

• 4.      U_T = —pI_i(pr) sin(pz), U_z = —pIo(pr) cos(pz),

• 5.           U_r = 0,U_z = —2, ф = r², p = —2z;

• 6.      U_r = r, U_z = —2z, ф = zr², p = —z² + r²/2;

ф = r J_i(pr) exp(pz), p = — Jo(pr) exp(pz);

ф = rJ_i(pr) exp(-pz), p = Jo(pr) exp(—pz);

ф = rI_i(pr) sin(pz), p = Io(pr) cos(pz);

ф = rI_i(pr) cos(pz), p = —Io(pr) sin(pz);

где p — произвольная положительная константа; Jo, Ji — функции Бесселя нулевого и первого порядков; Io,Ii — цилиндрические функции мнимого аргумента нулевого и первого порядков. Каждый из вариантов 1-4 представляет бесконечное множество линейно независимых функций, соответствующих различным значениям параметра p. Эти решения дают на оси симметрии r = 0 ограниченные значения U_z и нулевые значения U_T. Поэтому их линейные комбинации соответствуют течениям, в которых жидкость может достигать оси симметрии. Как замечено выше, для таких течений в формуле (8) константа А должна быть равна нулю.

Коэффициенты линейной комбинации этих функций могут зависеть от времени. Кроме того, масштабирующие коэффициенты при пространственных аргументах могут также зависеть от времени. В итоге получится нестационарная потенциальная соленоидальная скорость. Поясним это на примере линейной комбинации двух стационарных потенциальных соленоидальных скоростей Ui(r, z) = Ui_T (r, z)e _T + Ui_z(r, z)e_z и U2(r, z) = U2_T (r, z)e _T + U2z (r, z)ez- Пусть фі = ф1(r,z). ф2 = ф2(r,z) ii pi = pi(r, z). p2 = p2(r, z) — функции тока и потенциалы, соответствующие этим скоростям. Тогда для любых четырех гладких функций времени

/1 = .М^Ь = ^/2^(t),9i = 9i ^(t) >  ^0,92 = 92^(t) > ⁰ (11)

линейная комбинация U (r, z,t) = /_i(t)U₁<9_i(t)r, 9_i(t)z) + /₂(t)U ₂(92(t)r, 92(t)z) будет соленоидальной потенциальной скоростью. То есть для любого значения параметра А скорость V* (А, r, z)+U(r, z, t) будет принадлежать Q/r-семейству решений уравнений Навье-Стокса.

(V *)2 (V *+U )^

Поле давления можно будет вычислить по формуле p = p* + Аф — d;p+ 2^— ”—2—’ ^{в ко}" торой функция тока ^(r, z, t) = (/i (t)/9i(t)) фi(9i(t)r, 9i(t)z) + (/2(t)/92(t)) ф2(92(t)r, 92(t)z) 11 потенциал p(r, z,t) = (/i (t)/9i (t)) pi(9i(t)r, 9i(t)z) + (/2(t)/92(t)) p2(92(t)r, 92

Выбирая различные функции (11), можно получать разнообразные картины течения с меняющейся во времени формой линий тока и со скоростями, зависящими от времени. В частности, функции (11) могут быть периодическими, и периодической во времени будет картина течения. Для получения стационарных решений следует в качестве функций (11) выбирать константы.

Если рассматривается течение, в котором жидкость не достигает оси симметрии, то к приведенным выше шести решениям для потенциала можно добавить еще пять осесимметричных линейно независимых решений уравнения Лапласа, имеющих особенность на оси симметрии [24]. Кроме того, в формуле (8) константа А может быть не равной нулю.

Представляется, что сведения, приведенные в данном разделе, позволяют создавать разнообразный и достаточный для целей верификации запас точных решений уравнений Навье-Стокса.

7.    Некоторые свойства Q/r-семейства

Кроме линейности по скорости решения Q/r-семейства также обладают двумя интересными свойствами, отличающими эти решения от решений Тркала.

Под нелинейным слагаемым уравнения Навье-Стокса в зависимости от формы записи понимают либо вектор (V • V)V, либо вектор rot V х V. В любом из этих смыслов нелинейные слагаемые для решений из Q/r-семейства не равны нулю. Это одно из отличий от решений Тркала, в которых нелинейное слагаемое rot V х V равно нулю.

Нестационарные решения уравнений Навье-Стокса, полученные Тркалом из стационарных решений уравнений Эйлера с помощью умножения скорости на exp(- at), сами по себе в общем случае не удовлетворяют нестационарным уравнениям Эйлера. То есть в общем случае решения Тркала являются только нестационарными решениями уравнений Навье-Стокса. В отличие от этого скорость любого решения (как стационарного, так и нестационарного) из Q/r-семейства удовлетворяет и уравнениям Эйлера, и уравнениям Навье-Стокса (с различным распределением поля давления).

8.    Заключение

В рамках уравнений Навье-Стокса рассмотрены осесимметричные течения вязкой несжимаемой жидкости в потенциальном поле внешних сил. Получено семейство точных решений, среди которых есть как стационарные, так и нестационарные решения. У некоторых нестационарных решений картина линий тока меняется во времени. Любая линейная комбинация скоростей из найденного семейства является скоростью некоторого решения уравнений Навье-Стокса. И это «новое» решение также входит в полученное семейство точных решений. «Новое» поле давления не является суммой давлений «исходных» решений, но несложным образом рассчитывается через параметры «исходных» решений. У разных решений этого семейства линии тока в общем случае не совпадают. Исключение составляют лишь такие решения, поля скоростей которых переходят друг в друга при умножении на функцию времени (например, на константу). При этом для всех решений семейства нелинейное слагаемое rot V х V в уравнениях Навье-Стокса не равно нулю. Последнее обстоятельство представляется особенно интересным, поскольку обычно линейная комбинация решений нелинейного уравнения не является решением такого уравнения.

Полученные точные решения могут использоваться для верификации численных схем и других приближенных методов. А также для иллюстраций различных закономерностей вязких течений.