Semi-fragile Image Watermarking Algorithm Based on Region-Segmentation

With the popularity of the Internet, especially with the wide application of the multimedia technology, the security protection problem of multimedia information is becoming more and more pressing. As an effective protective means of the multimedia data, the digital watermarking techniques have become the research focus of international academia [1].

According to its characteristics, the digital watermarking can be categorized into three types, robust digital watermark, fragile digital watermark and semi-fragile digital watermark. Owing to the limitation of network bandwidth, we often transmit multimedia information by means of data compression. Therefore, the application of semi-fragile watermark will have a promising prospect because of its fragility and robustness.

Manuscript received January 19, 2009; revised June 16, 2009; accepted July 13, 2009.

For instance, semi-fragile watermarking algorithms are unceasingly coming to the fore in spatial domain, transform domain and some other domains based on physiological model [2-7].

There are many defects in existing semi-fragile watermarking algorithms [8-10], such as bad invisibility, imperfect robustness in some routine signal processing’s. The main reason lies in that they all used some fixed quantized parameters without considering the differences between different images. Moreover, while embedding watermark information they have not considered the new characteristics brought to carrier pictures by a regular signal process, so when extracting watermark, the robustness can not reach the maximum all the time. That is to say, they were not embedding watermark information according to the attack’s characteristics. According to the vision masking feature model of human visual system stated in reference [12], reference [11] quantizes the wavelet coefficient dynamically in block form and embeds a watermarking information bit in every wavelet coefficient block by adjusting its value. From the experiment results mentioned in reference [11], this algorithm is reasonable to some extent. However, after scrutiny of the inner-block wavelet coefficients adjustment scheme, we find some defects. Firstly, because the effect of conventional attacks to the whole image is uniform, the smaller quantized step area causes the higher tampering rate. Secondly, the wavelet coefficients are not to be negative after Haar wavelet transform, therefore, there are no negative adjustment coefficients in this case, the prove is omitted. Thirdly, in accordance with the adjustment scheme of wavelet coefficients which is no less than 0, theoretically it can not extract correct watermarking information, the prove is omitted. Finally, the embedded watermarking information is so little, the number of bits is only 1/256 that of the original image pixel count.

Based on human visual features, the paper establishes a new model of visual features and puts forward the Quantized Central Limit Theorem, coefficient redressal operator, the best restore probability, and the double-step embedding method. Based on this theorem, we use dynamic quantized approach to embed watermark in wavelet transform. Experiments show that better invisibility of carrier image and a better robustness to the image processing such as JPEG compression, noise adding and smoothing filtering can be achieved. Meanwhile, embedding information in a large amount, the number of data bits reaches to a quarter that of the original image pixels. It can also ascertain the position of vicious attack exactly.

In Section II, the visual model based on human visual features will be presented. In Section Ш , the digital watermark embedding process is illustrated. In Section ^ , the digital watermark extracting process is illustrated. In Section V , the precise location of vicious attack will be presented. In Section И , the experimental results are presented. Section ^ concludes the paper.

II. The Visual Model Based On Human Visual Features

LH

M m n

--X--

is the mean of wavelet transform coefficients

of LH. This process is the same to the other two coefficients D and D .

HL        HH

As defined above, the luminance coefficient reflects the luminance degree of the image block. The texture coefficient reflects the block-image’s changing degree in three directions as horizontal, vertical and diagonal. And the variation coefficient reflects the fluctuation degree of the image pixel values. They reflect the eye characters when human observe objects. Therefore, when it is in an equiprobable situation, we introduce the coefficient sum 2 and the region segmentation operator Z ■

LT 2 =-----+ 5 x-----, max L     max T

„ 8x D

^Z =-----.

to

max _D

According to the value of Z , it can divide the picture into two areas called texture area and smooth area

• A. Visual features of human eye

The visual characteristic that influences the human eye of the picture includi luminance masking, texture masking and frequency domain characteristics. According to physiological experiments, when observing objects, human eye has such characters as follows.

• •    Low sensitivity to additional noise in high luminance image region.

• •    Relatively lower sensitivity to image texture region than the smoothing region.

• •    Low sensitivity to the image’s high frequency information.

In accordance with those three characters mentioned above, when embedding watermark in the image region of high luminance, frequency and texture, it can make the carrier image achieve a good invisibility.

(segmentation method see section Ш ). Then introduce the quantization step parameters separately in different regions.

The coefficient sum 2 0 and step A 0 of the texture area can be defined as follows.

2 0 =---L0---+ 5 x---T0----, maxLxn0     maxTxn0

A ₀ = Round (log(2 ₀ +1) x ф )/10- to

the coefficient sum 2 1 and step A1 of the smooth area can be defined as follows.

2 1 =

L ₁

+ 5 x

T 1

max _L x n 1     max _T x n 1

A 1 = Round (log( 2 1 + 1) x фx 0.2)/10.

to

Where max _L is the maximum for normalizing L ,

B. Setting-up of the visual model

Taking the Haar wavelet as basic function and making the images do a two-dimensional discrete wavelet transformation, the coefficient will be a reflection of the three visual characters of human eye. Defining the three parameters for an image block I M _x N and a one-scale 2-D

DWT coefficient

S

as follows.

MN

• •    Luminance coefficient

L = 22 S Mn (i, j ).

i j 2 2

• •    Texture coefficient

max _T is the maximum for normalizing T , and max _D is the maximum for normalizing D . They can be calculated according to Figure 1. And 5 is the operator to adjust the rate of coefficient. In a general case, the value of the normalized lamination coefficient is very small, and the sensitivity of the human eye on low frequency components is higher than on high frequency components. Z is the region segmentation threshold, the result is shown in figure 2. L ₀ and T ₀ are the luminance coefficient and the texture coefficient of the texture area

T = 22

ij

S M^LHN ( i , j )

—x—

S M^HLN ( i , j )

—x—

+ S M^HN ( i , j )

—x—

• Variance coefficient

D = D LH ⁺ D HL ^{+ D}HH .

Where

D LH =     N  2 2 ^{( S}M N ⁽ i , ^j ) - ^M M N )

M N           x—        x—

----x-- 1 i j ^{2 2             2 2}

respectively, and n ₀ is the ratio of texture area size to picture size. L ₁ and T ₁ are the luminance coefficient and the texture coefficient of the smooth area respectively, and n 1 is the ratio of smooth area size to picture size. Round is the round operator. ф is the coefficient for experimental quantized step adjustment. In order to prevent the negative number, the coefficient sum adds 1.

Thus, where the human eye has less sensitivity, the quantized step is much bigger. That is, on the premise of no affecting image quality, if the intensity for embedding is greater, the robustness of the extracted watermark is stronger.

Take Lena as an example to explain the algorithm of this paper. The detailed values for the algorithm are shown in Table 1.

To illustrate the characters of the visual model, as shown in figure 3, the 256 x 256 Lena gray image is divided into many 64 x 64 blocks and labeled with sequence number in row. According to the divided block number which is listed depending on the descending order of quantized step length. We can see the comparison results of the visual models between reference [12] and this paper in Table 2.

Contrasting the result observed directly by human eyes and the experimental data can show that the model in this paper can manifest the visual features of human eye better.

Ш. Digital Watermark Embedding

• A.    Visual features of human eye

Some classical scrambling methods such as Arnold scrambling and magic scrambling are all based on the image of square pixel matrix. However, the scrambling method of this paper is suitable for image pixel matrix of any size.

The original watermarking information scrambling processes are as follows.

to Read-in the original watermarking image w m _x n .

to Based on secret key key1 , randomly produce an array that length is m x n and store it in W1.

to Read the element value k in sequence W 1 , then take out the value of the k^th element of w , and put it into the w ₂ in sequence.

to Obtain the scrambling watermarking matrix w ₂ .

• B.    Region segmentation operator

The Region Segmentation methods, such as edge extraction and gray threshold method, are all the methods based on space domain. They are only interested in the differences of the pixel values and did not considering the change among the values. Thus these methods will divide a lot of pixel points that unnecessary divide out to the smooth area and reduce the robustness of the image. The region segmentation method of this paper is based on frequency domain, considering the changes in three directions of horizontal, vertical and diagonal.

The region segmentation processes are as follows.

to Make the original image do one-scale twodimensional discrete Haar wavelet transform.

to According to the HL coefficient S M N , LH

—x— coefficient SMLH N , HH coefficient SMHHN and

—x—                 —x

22             22

expression to calculating Z .

to Intercept the 2 x 2 blocks of the high frequency coefficients HL, LH and HH in sequence, when all the values in the 2 x 2 blocks of the coefficients are less than Z , dividing the corresponding 2 x 2 block of the low frequency coefficient LL to the smooth area, otherwise, dividing it to the texture area.

• C.    Quantized central limit theorem

When we refer to watermarking techniques, there is a difficulty. It is how to adjust the data in watermark embedding region and how to make the carrier image obtain the best robustness when we extract the watermark. There are few references that give quantitative description. Many conventional attacks, such as noise adding and filtering, only make the value of carrier data changed. Giving quantized step A and defining the best restore probability p , we find out that p is the position that the restore probability is maximal after attacks when pixel value increasing during [0, (1 - p ) x A ] or decreasing during [ - p x A ,0] . As shown in figure 4, the number of the pixel points that the changing values falling in the slipping window is maximal, the slipping window’s height A is unitary, i is linearizing position of image pixel, AF is the variation of pixel value after attack.

Figure 1 Veins

Figure 2 Segmentation

• Table 1    Parameter values of Lena

Parameter values of Lena
Ф	p	Z	L 0	T T 0	S 0	П 0	A о	L 1	T 1	S 1	П 1	A i
225	0.5	1.6898	3670803	232844	1.2011	0.9104	11	427580	2523.5	0.65023	0.0896	2.3

• Table 2    Results of different visual features models

Visual Model	Results of different visual features models
reference [12]	7	15	10	6	11	8	9	13	14	4	16	12	3	2	5	1
This paper	10	6	7	14	13	9	11	15	16	4	8	3	2	12	5	1

Figure 3 Block-Division

Giving the best restore probability p and using step

A and integer operator to quantify a positive number x, supposing that x = n x A + rem (x, A).

rem(x, A) is the remainder which has the same sign as x. The quantified value of x is n. If the parity of n is homologous with that of the watermarking data, then we make the following adjustments and define the adjusted value x as x = n x A + p x A.

As long as the carrier data x' changes in the range of [-(p xA),0] or [0,(1 - p) xA] , which we call it robust region, the parity of its quantified data can be kept unchanged, that is, the watermark data can be correctly detected. On this condition, the detected robustness of the carrier data is the greatest, and the revision change of x will not exceed the max(p x A,(1 - p) x A).

Similarly, if the parity of n is repugnant with that of the watermark data, it will be necessary to adjust the parity of quantified value, that is, it is necessary to define the adjusted value x ^'

x = ( n -1) x A + p x A, if rem ( x , A) <  p x A;

x = ( n +1) x A + p x A , if rem ( x , A) >  p x A.

Therefore as long as the carrier data x changes in the range of [-(pxA),0] or [0,(1 -p)xA] , the parity of its quantified data can be kept unchanged and the revision change of x will not exceed A . The three positions of x in the entire adjustment process are shown in Figure 5.

Similarly, when x is less than 0, we can also use the same strategy. Based on the above analysis, we can sum up and deduce the following theorem.

Quantized Central Limit Theorem

Using step A to quantify transform domain coefficient S _M ^LL _N , if the best restore probability is p , a —x— 22

quantified coefficient

^LL can be obtained. When

MN

— x- watermark data w is extracted from carrier image, it can make a best robustness by adopting the following coefficient adjustment approaches.

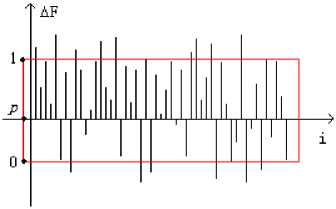
Figure 4 Probability p definition

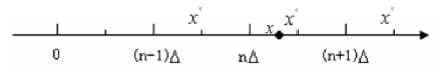
Figure 5 Value adjusting in quantization to If mod(QML N (i, j),2) = w(i, j) ,the adjusted carrier x data is

® if s M^ln >0 , x

'

^SM N ⁽ i , j ) = ^QM N ⁽ i , j ) ^{x A +} p ^{x A} ;

—x—        —x to if sMln <0,

—x—

S Mn ( i , j ) = Q — n ( i , j ) xA- p xA .

—x—         —x

22       22

to If mod(Q— n (i, j),2) # w(i, j), the adjusted carrier data is to if S— n > 0 and rem (x, A) < p x A , x

S —L N ( i , j ) = ( Q — N ( i , j ) - 1) xA + p xA ;

—x—         —x

22        22

to if S — _N > 0 and rem ( x , A ) >  p x A , x

S M^Ln ( i , j ) = ( Q MLN ( i , j ) + 1) xA + p xA ;

—x—          —x

22        22

to if S — _N < 0 and rem ( x , A)| <  p x A , x

S —n ( i , j ) = ( Q MLN ( i , j ) + 1) xA- p xA ;

—x—         —x

22        22

to if S ML _N < 0 and rem ( x , A)| >  p x A , x

'

S ML N ( i , j ) = ( Q M^L N ( i , j ) -1) xA - p xA . —x—        —x

22      22

Where i = 1,2,..., — , j = 1,2,..., — . The proving process is omitted. From Figure 5, it can be easily concluded that restore probability p is important to coefficient adjustment. Through the analysis of the result of normal attacks such as noise adding, pepper salt etc, maximal p is about 0.52 and minimal p is about 0.42.

• D.    Coefficient redressal operator ^

In general, through operator Round can change the IDWT double-precision number to unsigned 8-bit integer. But the defect of Round is that it can not extract the whole correct watermark even if there is no any attack, because if we do DWT after Round , there is much coefficient changed. Reference [13] is aware of this problem, but it can not adjust IDWT real number precisely without knowing the expression between DWT LL coefficient and carrier image data. We can prove that the low frequency coefficient of one-scale twodimensional discrete Haar wavelet transform is directly related to the data blocks of original image. That is, the corresponding data block to the low-frequency wavelet coefficient LL_L ( i , j ) of the original image is

I(((i - 1) x 2 ^L + 1): (i x 2 ^L f(fj■ - 1) x 2 ^L + 1): ( j x 2 ^L )). to

If we keep the data sum unchangeable through operator ^ , we can extract whole correct watermark. Then the operating process of the algorithm of operator ^ is as follows.

to Get the adjusted coefficient S “ _N ( i , j ).

тX т to Consult expression to, and then calculate its image data block.

to Segement double-precision real number into integer part A and decimal fraction part B .

to Calculate sum 5 of B .

to Sort B descending.

to Get the max decimal fraction position, and then add one to its integer part and subtract one from s .

to Repeat step to until 5 <  0.5 and increase each pixel value only once within 255.

to Repeat step to to to until the whole image block is processed.

to The adjusted integer part is unsigned 8-bit integer.

• E.    Digital watermark embedding

Suppose the original image is

I m x n = { g ( i , j ),1 ^ i <  M ,1 ^ j <  N }.

Where g ( i , j ) is the pixel value of the image in row i and column j . After being scrambled, the watermark binary image is

M N

W = { w ( i , j ) e {0,1},1 <  i < — ,1 <  j <  y} .

The watermark embedding algorithm is as follows.

to According to 1X1 size of the original image zoom the original watermark information.

to Scramble the watermark information that will be embedded.

to Make the original image do one-scale twodimensional discrete Haar wavelet transform.

to According to the LL coefficient S ML _N , expression

X to and to, figuring out A 0 and A1.

to Get q Mn ( i , j ) ^from S ML _N quantified by A 0 ^and A ! .

Make the LL coefficient quantized adjustment according to the Quantized Central Limit Theorem.

® If mod(QM n (i, j),2) = w(i, j), the adjusted carrier X — data is

S M^Ln ( i , j ) = Q\

---X---

*LL «( i , j ) x A, + p x A. . M N ,             ij               ij

2 ^X 2

® ^{If mod(Q} M^L N

--X--

(i, j),2) * w(i, j), the adjusted carrier data is

If rem ( x , A j ) <  p x A j ,

S ML_yN ( i , j ) = ( Q S.» ( i , j ) - 1) XA j + p XA j ;

2 ^X 2                        2 ^X 2

If rem ( x , A j ) >  p x A j ,

S M ®⁽ i , j ) =⁽ Q M ®⁽ i , j ) ⁺ 1) ^{X A} j ⁺ p ^{X A} j '

2 ^X 2                        2 ^X 2

Where S _M ^LL _N ^' ( i , j )   is the adjusted coefficient,

-X— i = 1,2,...,

M

-y’ j = I, ² ,-,

N

to Make IDWT, adjust the double-precision real number by operator ^ and change the double-precision real number to unsigned 8-bit integer. Then the image is obtained. We call it carrier image, in which watermark is embedded.

W. Digital Watermark Extracting

• A.    Digital watermark extracting

The process of digital watermark extracting is the reverse of embedding. The detailed process is as follows. to Make the carrier image do one-scale two-dimensional discrete wavelet transform.

to Quantify coefficient LL by A ₀ and A 1 .

to Express the watermark extracting method as '

w(i, j) = mod(Qm n (i, j),2). --X-- to Repeat step to until all bits are extracted.

to Anti-scramble the extracted watermark information.

In order to guarantee the failed rate of extracted watermark value, we define tamper rate of the extracted watermark and original watermark as

F =

^^ ^w ( i , ^j ) © ^w ( i , ^j )

ij

MN

— X —

Set a threshold value t . If F = 0 , it means the image has not been attacked. If F <  t , it means the image has been processed by the conventional attack. If F >  t , it indicates the image has been viciously attacked.

• B.    Watermarking information anti-scrambling algorithm The extracted watermarking information antiscrambling processes are as follows.

to Read-in the extracted watermarking information '

W m x n .

to Obtain the array W 1 that produced in scrambling process.

to Read the element value k in sequence W 1 , then take out the value of W m x n in sequence, and put it into the k ^th element of the w ₁ .

to Obtain the watermarking matrix W 1 .

V. Precise Location Of Vicious Attack

According to expression to , when L = 1, there will be a low-frequency wavelet coefficient to each 2 x 2 image data. So it is easy to find the position directly where has been changed by vicious attacks from the changed position of watermark value.

И. Experimental Results

• A.    Invisibility of digital watermark

  In this paper, 256 x 256 gray image Lena is selected as the original image and a 128 x 128 binary image is selected as the watermark image. The watermark embedding and extracting of normal condition are shown in Figure 6. When ф = 225 , the image PSNR reaches 38.4455dB. From the experimental results, the invisibility of carrier image is good. If we reduce the adjusting coefficient ф , the carrier image can have a better invisibility, but its anti-attack capability will be reduced. So it is necessary to select a balance position that the PSNR is between 38dB and 42dB.

• B.    Robustness of digital watermark

In order to test the robustness of this algorithm, we use JPEG compression, noise adding, filtering and some other image processing approaches to process carrier image. Take the Lena images for example, the experimental results are shown in Table 3.

From the experimental data, each adjusting strategy improves the result of this algorithm greatly, which makes an expected result. The JPEG compression ratio is the size ratio of the original image and compressed image. The best restore probability of each attack is from our experiments. PSNR is the peak signal to noise ratio of the carrier picture before attacking. If we know the attack firstly, embedding watermark by using the best restore probability shown in Table 3, it can get minimal tamper rate. Since watermark data is carried in the image low-frequency region, the watermark information will lose after high-pass filtering, and then it can’t be normally extracted. It is the only common attack that this algorithm is unable to resist. But we can embed another watermark copy in high DWT coefficient by using DCT, which is called bi-watermarking technique [15].

Figure 7 is the extracted watermark images of Lena after being attacked by various kinds of conventional attacks. When coefficient adjustment operator is ^ , P = 0.5, ф = 225 .

When attack the carrier image, if the change amount of pixel value has exceeded the endurance of the watermark, it is easy to orient the position of vicious attack directly according to expression to , as is illustrated in Figure 8.

Table 3 The watermark detection results for various attacks(tamper rate)

Attack	Attack parameter	p=0.5 Operator Round		p=0.5 Operator ^		p=0.45 Operator ^		restore probability p
		ф = 195 t = 0.25 A o = 11 A 1 = 2 PSNR=38.43	ф = 225 t = 0.24 A o = 11 A 1 = 2.3 PSNR=38.45	ф = 195 t = 0.25 A o = 11 A 1 = 2 PSNR=38.45	ф = 225 t = 0.24 A 0 = 11 A 1 = 2.3 PSNR=38.46	ф = 195 t = 0.35 A 0 = 11 A 1 = 2 PSNR=38.45	ф = 225 t = 0.24 A 0 = 11 A 1 = 2.3 PSNR=38.48
Filtering	Low filter 3×3	0.24518	0.23383	0.24017	0.23602	0.24548	0.23511	0.47
	median filter 3×3	0.10974	0.095154	0.09375	0.08905	0.092529	0.091003	0.43
image cut	(M/4+1)×(N/4+1)	0.075012	0.053894	0.053101	0.05298	0.052124	0.053223	0.46
	(M/2+1)×(N/2+1)	0.22913	0.21051	0.21051	0.21014	0.20935	0.21075	0.50
Noise adding	Pepper salt 1%	0.041321	0.020264	0.021545	0.021179	0.020813	0.020752	0.50
	Pepper salt 2%	0.062073	0.041931	0.042603	0.04199	0.041992	0.039429	0.51
	Pepper salt 3%	0.081482	0.062683	0.059265	0.06012	0.061462	0.057617	0.51
	Gaussian 35dB	0.19702	0.19958	0.18622	0.18964	0.19214	0.1886	0.44
	Poisson 35dB	0.12134	0.12909	0.11884	0.11658	0.12048	0.12042	0.51
JPEG compress	Ratio 3	0.03009	0.019226	0.020447	0.01239	0.022522	0.011536	0.42
	Ratio 5	0.061462	0.054321	0.054382	0.05017	0.05719	0.049927	0.49
	Ratio 7	0.13257	0.13141	0.12683	0.12891	0.13116	0.12457	0.44

W Original image to Watermark image

^M ^Ж to Extracted to Carrier image

Figure 6 Watermark embedding and extracting

^^, 44-43. 44-43.

•йж |-е!1ж ^jiit

(a) Median filter 3 X 3 ^Median filter 3 X 3 (c) Cut 1 2

(d)Cut 1/4 (e)Pepper salt 1% (OPepper salt 2% ш ilii Ш^ -SiljlL -g’jilfc ^J4t

M Pepper salt 3% ^ Gaussian 35dB (i)Poisson 35dB

(D JPEG ratio 3 W JPEG ratio 5 (O JPEG ratio 3

(a) Tampered image

Figure 8 Tampered region detection

Figure 7 Extracted watermark after normal attack

(b) Orientation image

D. Missed detection and false detection probability

In order to validate the characteristics of this algorithm, based on the missed and false detection probability, we make a comparison between the algorithms in references [1], [3], [4] and this paper. Considering the fairness and objectivity, we take 1000 images ^[16] as experimental objects. And we take the recognized 8 x 8 block as experimental objects and use the common attacks to test the missed and false detection probability. Moreover, we make different algorithms quantified with PSNR on benchmark of Lena. The results are shown in Table 4.

^. Conclusions

The main innovations of this paper can be summarized as follows. Firstly, having set up a new visual model according to visual characteristic of the human eye, provided the mathematical expression of the visual model. Secondly, according to the image characteristics that reflected by wavelet transform coefficients, brought forward the region segmentation operator to segment the image. Thirdly, it brought up the idea which embedding watermark based on the attacks’ characteristic, and obtained the best restore probability of different conventional attacks from a large number of experimental data. Fourthly, according to the best restore probability bought forward the quantized central limit theorem based on the attacks' characteristic, which applies to adjusting the coefficients in general transform domain and makes semi-fragile watermarking embedded through dynamic quantization achieve the greatest robustness. Finally, proposed and proved the wavelet transform domain coefficient redressal operator, it made the revised IDWT LL coefficient consistent with the adjusted coefficient that after quantized.

From the experimental results, we conclude that by adopting the human visual model, the algorithm in our experiment can adjust the wavelet decomposition coefficients in accordance with the Quantized Central Limit Theorem, operator Z and the best restore probability p . It is able to protect the copyright of digital image. Simultaneously this algorithm can accurately detect vicious attacks’ position. As a result, its robustness is superior to other general watermark algorithms with bits of watermark reaching a quarter of the original image’s size.

There will be the following research tasks in the future. Firstly, how to adjust visual model of human eye features and make the calculation of quantize steps keeps invariant before and after the conventional attacks, thus subtract the additional information. Secondly, on the premise of keeping the invisibility of carrier image, combining the best restore probability, how to adjust the size of quantization step just to the integral multiples of the change amount of wavelet coefficient value, thus make the tamper rate of the extracted watermark is minimum. Thirdly, segmenting the image according to the concentration and dispersion degrees, further raise the invisibility and robustness of the image. Fourthly, due to the different scrambling position will produce the different extraction effect, needing to choose the best image scrambling algorithms or the image encryption algorithms through the further experiment. Finally, according to trend of the watermark research at present, the self-recovery watermarking technique will be the focus of the watermarking integrity research, so can introduce the self-recovery technique into the semi-fragile image watermarking algorithm.

Table 4. The missed detection and false detection probability

Watermarking algorithm	Simulated attack missed rates ( % )	False detection probability of routine signal processing ( % )
		No attack	JPEG compression ratio 1.5	Histogram equalization	Gaussian noise ( 35dB )	Salt& pepper ( 1% )	Low- Pass Filtering ( 3^3 )
Reference [1]	0.4	3.7	5.0	8.3	0.3	8.3	6.8
Reference [3]	2.5	1.9	9.5	12.7	14.9	2.8	2.0
Reference [4]	13.2	1.4	11.7	23.6	2.8	11.5	5.6
This paper	0.01	0.0	2.3	1.0	0.4	1.1	2.2

Acknowledgment

This paper is supported by Chinese NSF 60373000, Hunan NSF 07JJ3124, Hunan Provincial Science and Technology Plan 2009GK3096, HUNAN graduate student innovation foundation, Hunan Provincial education department foundation 06d042, Hunan Province public security department foundation [2008]14, CSUFT science foundation 06Y003, 07007A, 2006sx02.