Сепарация слабопроводящих суспензий в бегущем электрическом поле

Применение электрических методов для очистки жидкостей, обладающих большим удельным электрическим сопротивлением (растительные масла, биотопливо, нефтепродукты и др.) обосновано малыми энергозатратами, экологичностью, малым гидравлическим сопротивлением аппаратов. В настоящее время разработан ряд аппаратов электрической очистки и сепарации слабопроводящих жидкостей в электрическом поле, в которых применяют постоянный или переменный электрический ток промышленной частоты высокого напряжения, создающий постоянное или пульсирующее электрическое поле [1, 2]. В таких устройствах используются силы электрофоретического и диэлектрофорети-ческого взаимодействия, позволяющие осаждать частички взвеси на электроды. Такой подход требует периодической очистки электродов. Кроме этого, отсутствует возможность разделения частиц с разными электрофизическими свойствами. Разделить такие частицы актуально с точки зрения использования полученных веществ. Например, разделение взвеси подсолнечного масла позволяет получить ценные компоненты – клетчатку и фосфатиды.

Применение бегущего электрического поля, созданного системой многофазных электродов, позволяет осуществлять направленное движение частиц взвеси вдоль рядов электродов [3]. Используя этот эффект, можно не только создавать электроочистители непрерывного действия, но и электросепараторы, способные разделять частицы с разными электрофизическими свойствами.

В электрическом поле на поляризованную частицу действует сила [4]:

—

——

—

f . L dE

F = Re A Ex — + E ^E + Ez ^E x         y         z d2

V V

d x

d y

;

ч

A = 4nsca3----

^{— 8}c ) ^—

f -

i

■ ч ^- )

—

( 8 4 + 28_c ) ^—

V го го 7

, i -ч+2

V to

го 7

где £ _с , е _ч - диэлектрическая проницаемость среды и частицы соответственно, Ф/м;

σ с , σ ч – удельная электропроводность среды и частицы соответственно, См/м;

a – радиус частицы, м;

ω – угловая частота, рад/с;

—

E – комплекс вектора напряженности электрического поля, В/м.

Ex, Ey, Ez – компоненты вектора, комплексно сопряженного с век-^— тором E, В/м.

В соответствии с формулой (1) в системе многофазных пластинчатых электродов на поляризованную частицу действует — сила Fч1 со стороны пульсирующего поля, которая перемещает частицы в область максимального поля между пластинчатыми —— электродами, и сила Fч2 со стороны бегущего поля, которая перемещает частицы вдоль рядов электродов (риcунок 1).

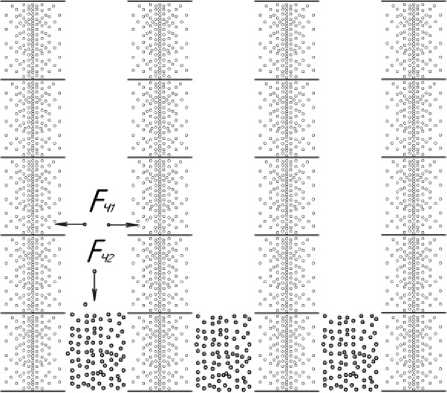
Рисунок 1 – Система многофазных пластинчатых электродов

Для исследования динамики частиц в работе [4] аналитически описано электрическое поле методом комплексного по- тенциала, и исходя из выражения (1) получены формулы для поля сил в двухрядной системе многофазных электродов:

B =

dW ro

dro

С =

d2W ro

dro2

F = A •B

——

z =

1

•

D • C

—

H • B

D

hn

( D ) ³

;

hn              hm

— Е ln (ro — ак) +—Е ln (ro

П к = 1

П = 1

—

c _i );

n

Е

^U1 ( к — 1 )

П ^ к = 1

ro

—

-

-

1

nU

U1k

ak

1 ( к — 1 )

-

- Е _{z x} ^п ( ^к = ^{1 (} ro ^{— а}к )

D =

dz

dro

m

: — 1 U

+

Е

2i

-

^U2 ( i + 1 )

+

U1n

—

U21

\

і = 1

ro

-

c

ro

-

c1

;

U 1k

m — 1 U

+

2i

-

^U2 ( i + 1 )

Е _z . i = ^{1 ( ro — c}i + 1 )

+

U1n

-

U21

\

^{( ro — С}1 )

;

H =

d2z

h

^™

h

n

Е

1

m

+ Е

1

\

П

^ к=1ro

—

ak

і = 1 ГО

^“

ci 7

;

n

1

dro

- Е ------2

п^ к=1 (ro — ак )

m

1

+ Е ------2

i = 1 (ro — ci)

,

где W – комплексный потенциал, В;

z – функция, которая конформно отображает верхнюю полуплоскость ϖ комплексной плоскости на многоугольник;

h – размер межэлектродной области (расстояние между рядами электродов), м;

a k , с i – параметры отображающей функции;

U ik – потенциал электродов, В.

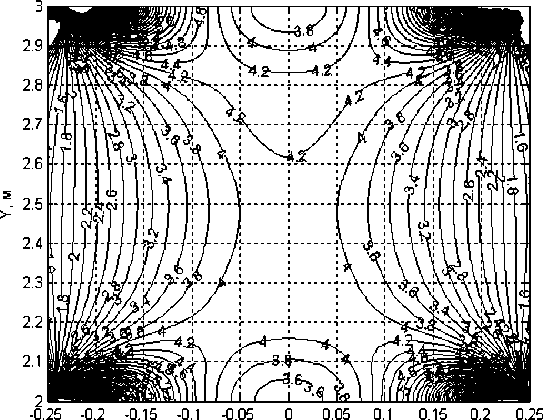
Визуализация поля сил в соответствии с формулами (2…6) программными средствами MATLAB (рисунок 2) позволила определить, что Y-составляющая силы, которая действует на частицы со стороны бегущего поля, незначительно изменяется вдоль координаты Y. Ее величина для электродной системы с размерами l = 0,5 м; h = 1 м составляет F ^* = 4 Н при величине параметра A = 1 Н∙м³/В² и действующем напряжении на электродах U ik = 1 В.

X, м

Рисунок 2 – Поле Y-составляющей силы при соотношении размеров межэлектродной области l/h = 0,5

Динамика движения частиц в бегу- щем электрическом поле исследовалась на основании второго закона Ньютона с учетом силы действия электрического поля и силы сопротивления среды. В результате было получено нелинейное дифференциальное уравнение второго порядка, которое описывает движение частицы:

d2 y + 9n dy dt2 2a2 p dt

3F* A • U²

4 mi' p h³

, (7)

где ρ – плотность вещества частицы, кг/м³;

η – динамическая вязкость, Па∙с;

В общем случае такое уравнение не имеет аналитического решения, но для постоянной векторной функции F ^* оно может быть сведено к линейному уравнению с постоянными коэффициентами и правой частью. Решение такого уравнения состоит из общего решения соответствующего уравнения без правой части и частного решения. Искомым решением является:

• ^V0 ^C3 ^үY         V o ^C3 _{r t}

У =------- e + У о ---⁺ C ' t,

Y             Y

С = Fau2

• ³   6 nq ah ' ,

9n

Y = -F^, 2a p где V0 - начальная скорость, м/с;

у о - начальная координата, м.

Если на электроды подавать две системы напряжений разной частоты с разным чередованием фаз, то в межэлектродной области создаются два электрических поля, бегущих встречно. При определенных частотах этих полей можно добиться разделения двух частиц с разными электрофизическими свойствами. Это следует из вида зависимости силы от частоты (1), которая имеет один максимум [5]. На частицу взвеси будет действовать сила, равная сумме сил от отдельных бегущих полей, которые могут быть направлены как в одну сторону, так и встречно:

F1 = F1 («1) + F1 («2),     (9)

где F 1 - сила, действующая на частицу в бегущем электрическом поле при частоте го 1 , Н;

F 2 - сила, действующая на частицу в бегущем электрическом поле при частоте го 2 , Н .

В соответствии с формулами системы (1) вид зависимости силы от частоты предопределяется видом зависимости мнимой части комплексного параметра А от частоты, который в свою очередь зависит от электрофизических свойств частицы и среды ( а с , Е с , а ч , Е ч ). Если в жидкости находится вторая частица с другими свойствами, то на нее будет действовать сила

F 2 = F 2 ( « 1 ) ^{+ F}2 ( « 2 ) , (10) которая определена другим видом зависимости мнимой части комплексного параметра А от частоты. На рисунке 3 построены зависимости величины силы от частоты для двух частиц с разными электрофизическими свойствами.

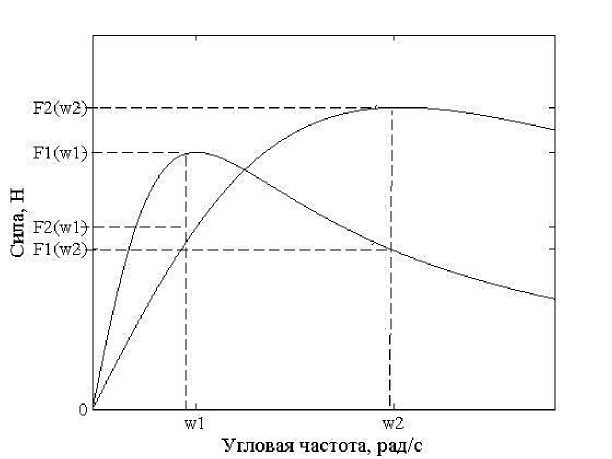
Рисунок 3 - Зависимости силы от частоты для двух частиц с разными свойствами

Если направления чередования фаз потенциалов электродов двух частот противоположны, то в межэлектродной области возникают два встречно бегущих электрических поля. В этом случае формулы (9) и (10) принимают вид:

• F, = F, («1) - F1 («23;

F2 = F, («1) - F2 («2), (11) и тогда в соответствии с рисунком 3 при значениях го1 и го2, которые соответствуют максимумам функций F1 (го) и F2(го), F1 >0, а F2<0. То есть силы направлены в проти- воположные стороны.

Для решения уравнения движения в поле двух частот по формулам системы (8) коэффициент C 3 находится по формуле

С з =

F* (A («1) - A («2 ))U2 бп^аһ3

На рисунке 4 показаны графики движения двух частиц с разными электрофи- зическими свойствами в бегущих электрических полях двух частот. Зависимости рисунка 4 построены для жидкости (подсолнечное масло) со следующими свойствами: Ос = 10-9 См/м; £с = 3,240-9 Ф/м; п = 0,054 Па-с и частицы: a = 50 мк, ρ = 1300 кг/м3, размеров области: h = 2 мм; l/h = 0,5. Движение частиц начинается с точки с координатой Y=0. Напряжение на электродах – 2 кВ.

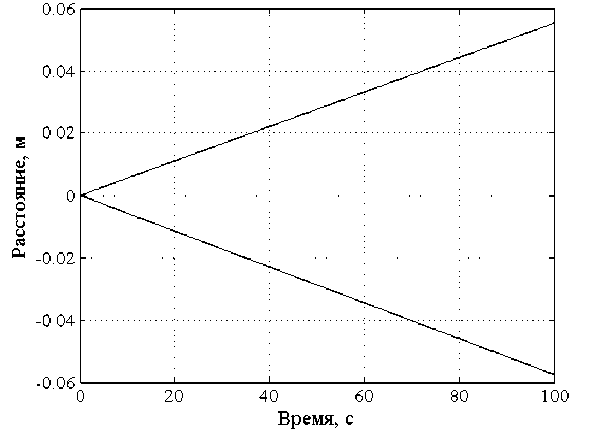
1 - О ч = 10 —7 См/м, ^ ч = 2,1 -10 — ¹¹ Ф/м; 2 - О ч = 4-10 " ⁸ См/м, ^ ч = 2,9• 10^-11 Ф/м

Рисунок 4 – Зависимости Y-координаты частиц от времени

Из полученных закономерностей следует, что частицы за 100 с разойдутся на расстояние 110 мм и будут разделены по признакам электрофизических свойств.

Теоретические исследования динамики частиц в двух бегущих полях разной частоты показывают возможность разделения их по признаку электрофизических свойств: диэлектрической проницаемости и удельной электропроводности. Причем на процесс разделения влияет как напряжение на электродах, так и частота электрического поля.

Для подтверждения полученных результатов были проведены экспериментальные исследования по разделению частиц шрота подсолнечника разной влажности. Использовался шрот влажностью 6% и 14%, который добавлялся в рафинированное подсолнечное масло в равных долях. Содержание шрота каждой из фракций составляло 0,25%. Предварительно были определены электрофизические характеристики приготовленной суспензии по методике [6]. Частицы первой фракции имели удельную электропроводность 4,4∙10-8 См/м, а диэлек-22

трическую проницаемость – 4,4∙10-8 Ф/м. Угловая частота, которая соответствует максимальной силе, для этой фракции составляет 446 рад/с. Частицы второй фракции имели удельную электропроводность 4,3∙10-7 См/м, а диэлектрическую проницаемость – 7,2∙10-8 Ф/м. Угловая частота, которая соответствует максимальной силе, для этой фракции составляет 3215 рад/с.

В экспериментальных исследованиях использовалась камера с двурядной системой электродов с h = 5 мм и l/h = 0,5. Длина камеры составляет 80 мм, поэтому для полного разделения фракций максимальное расстояние, которое должна преодолеть частица каждой фракции, составляет 80 мм. На электроды подавалось четырехфазное напряжение 7,2 кВ.

Содержание шрота в масле определялось по ГОСТ 5481-89. Пробы масла отбирались через 200 с.

Теоретические зависимости рисунка 5 строились по формулам (8) и (12) с учетом гранулометрической характеристики шрота.

Сравнение полученных экспериментальных результатов хорошо согласуется с теоретическими (рисунок 5). Расхождение не превышает 11%.

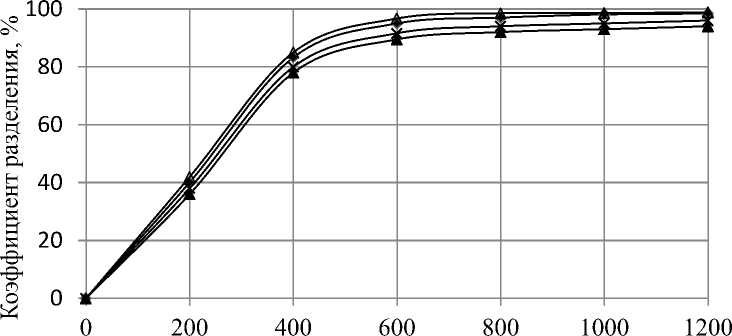
Время, с

• —♦— теоретическая зависимость для первой фракции

^s— теоретическая зависимость для второй фракции

• —*— экспериментальная зависимость для первой фракци и

э кспериментальная зависимость для второй фракции

Рисунок 5 – Динамика разделения шрота подсолнечника разной влажности

Таким образом, теоретически обоснована и экспериментально подтверждена возможность разделения частиц суспензии с разными электрофизическими свойствами в поле двух встречно бегущих электрических полей, созданных многофазными системами электродов.