Сепарация слабопроводящих суспензий в бегущем электрическом поле
Автор: Назаренко Игорь Васильевич
Журнал: Вестник аграрной науки Дона @don-agrarian-science
Рубрика: Механизация и электрификация животноводства, растениеводства
Статья в выпуске: 3 (23), 2013 года.
Бесплатный доступ
На основании теоретических и экспериментальных исследований динамики частиц обоснована возможность разделения частиц суспензии с разными электрофизическими свойствами в бегущем электрическом поле пластинчатой многорядной системы электродов.
Бегущее электрическое поле, сепарация, слабопроводящая суспензия, электрод
Короткий адрес: https://sciup.org/140204440
IDR: 140204440 | УДК: 66.086.2
Текст научной статьи Сепарация слабопроводящих суспензий в бегущем электрическом поле
Применение электрических методов для очистки жидкостей, обладающих большим удельным электрическим сопротивлением (растительные масла, биотопливо, нефтепродукты и др.), обосновано малыми энергозатратами, экологичностью, малым гидравлическим сопротивлением аппаратов. В настоящее время разработан ряд аппаратов электрической очистки и сепарации слабопроводящих жидкостей в электрическом поле, в которых применяют постоянный или переменный электрический ток промышленной частоты высокого напряжения, создающий постоянное или пульсирующее электрическое поле [1, 2]. В таких устройствах используются силы электрофоретического и диэлектрофорети-ческого взаимодействия, позволяющие осаждать частички взвеси на электроды. Такой подход требует периодической очистки электродов. Кроме этого, отсутствует возможность разделения частиц с разными электрофизическими свойствами. Разделить такие частицы актуально с точки зрения использования полученных веществ. Например, разделение взвеси подсолнечного масла позволяет получить ценные компоненты – клетчатку и фосфатиды.
Применение бегущего электрического поля, созданного системой многофазных электродов, позволяет осуществлять направленное движение частиц взвеси вдоль рядов электродов [3]. Используя этот эффект, можно не только создавать электроочистители непрерывного действия, но и электросепараторы, способные разделять частицы с разными электрофизическими свойствами.
В электрическом поле на поляризованную частицу действует сила [4]:
f . L дE
—
—
——
F = Re A Ex — + E — + Ez ^E x y z дz
——
V V
дx
дy
( °ч ° с )
—
>
A = 4nec a
—
V та to у i -ч- + 2 -с
ю у
где εс, εч – диэлектрическая проницае мость среды и частицы соответственно, Ф/м;
σ с , σ ч – удельная электропроводность среды и частицы соответственно, См/м;
a – радиус частицы, м;
ω – угловая частота, рад/с;
^—
E– комплекс вектора напряженности электрического поля, В/м.
E , E , E – компоненты вектора, комплексно сопряженного — с вектором E, В/м.
В соответствии с формулой(1) в системе многофазных пластинчатых электродов на поляризованную частицу действует сила F со стороны пульсирующего поля, которая перемещает частицы в область максимального поля между пластинчатыми электродами, и сила F со стороны бегущего поля, которая перемещает частицы вдоль рядов электродов (рисунок 1).
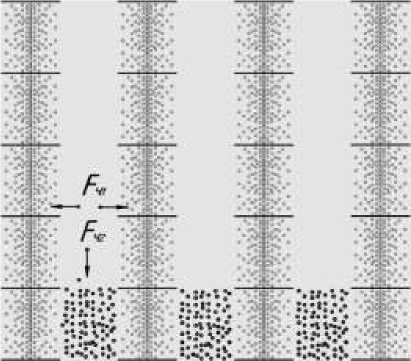
Рисунок 1 – Система многофазных пластинчатых электродов
Для исследования динамики частиц в работе [4] аналитически описано электрическое поле методом комплексного потен-
F = A • B
D
D • C
•
z =
hn
dW
dra d2W
dra
циала и, исходя из выражения (1), получены формулы для поля сил в двухрядной системе многофазных электродов:
—
H • B
hn hm
П k = 1
П i = 1
- e ' - 1 ) Un +
n ^ k=- ra - ak
m - 1 U2i U2 ( i + 1) + Uin - U21
i=1 ra - Ci+1 ra - C1 v
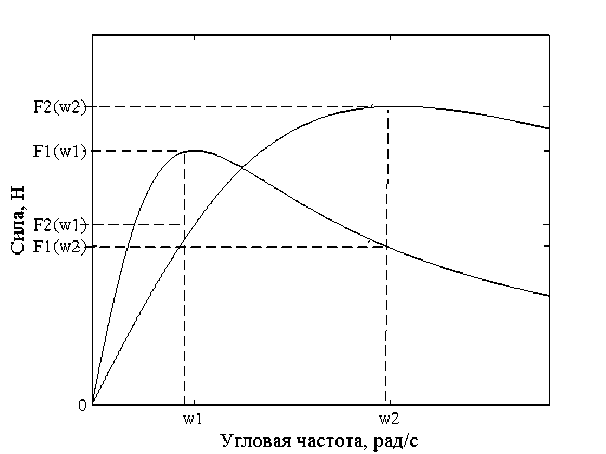
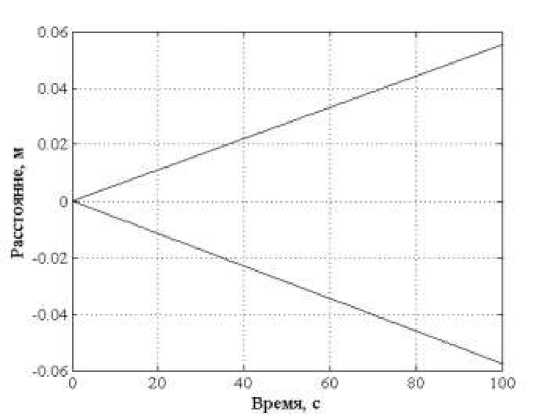
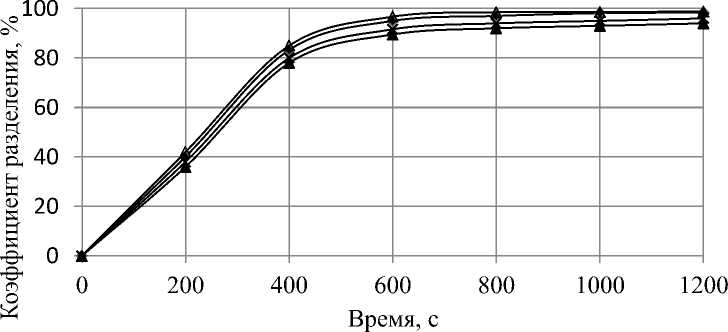
1 D = dz-dra h ( n 1 E n ^ k=1ra - ak m 1 + E----i=1ra - ci J d z h n 1 dra2 n ^k=1 (to - ak ) m 1 ) + E------Z i=1 (ra - ci)2 J где W – комплексный потенциал, В; z – функция, которая конформно отображает верхнюю полуплоскость ϖ комплексной плоскости на многоугольник; h – размер межэлектродной области (расстояние между рядами электродов), м; ak, сi – параметры отображающей функции; Uik – потенциал электродов, В. Визуализация поля сил в соответствии с формулами (2–6) программными средствами MATLAB (рисунок 2) позволила определить, что Y – составляющая силы, которая действует на частицы со стороны бегущего поля, незначительно изменяется вдоль координаты Y. Ее величина для элек- параметра A = 1 Н∙м3/В2 и действующем тродной системы с размерами l = 0,5 м; напряжении на электродах Uik = 1 В. h = 1 м составляет F* = 4 Н при величине м Рисунок 2 – Поле Y-составляющей силы при соотношении размеров межэлектродной области l/h= 0,5 Динамика движения частиц в бегущем электрическом поле исследовалась на основании второго закона Ньютона с учетом силы действия электрического поля и силы сопротивления среды. В результате было получено нелинейное дифференциальное уравнение второго порядка, которое описывает движение частицы: d2y 9п dy _ 3F* A • U2 dt2 2a2p dt 4ла3p h3 где ρ – плотность вещества частицы, кг/м3; постоянными коэффициентами и правой η – динамическая вязкость, Па∙с. В общем случае такое уравнение не имеет аналитического решения, но для постоянной векторной функции F* оно может быть сведено к линейному уравнению с частью. Решение такого уравнения состоит из общего решения соответствующего уравнения без правой части и частного решения. Искомым решением является: У = ----3eY + Уо Y V0 - C3 Y + C3t, С3 = F*AU2 6nqah3 Y = 9n 2a2 p где V0 – начальная скорость, м/с; y0 – начальная координата, м. Если на электроды подавать две системы напряжений разной частоты с разным чередованием фаз, то в межэлектродной области создаются два электрических поля, бегущих встречно. При определенных частотах этих полей можно добиться разделения двух частиц с разными элек- трофизическими свойствами. Это следует из вида зависимости силы от частоты (1), которая имеет один максимум [5]. На частицу взвеси будет действовать сила, равная сумме сил от отдельных бегущих полей, которые могут быть направлены как в одну сторону, так и встречно: F1 = F1 (Ш1) + F1 (^2), (9) где F1 – сила, действующая на частицу в бегущем электрическом поле при частоте го1, Н; F2 - сила, действующая на частицу в бегущем электрическом поле при частоте го 2, Н. В соответствии с формулами системы (1) вид зависимости силы от частоты предопределяется видом зависимости мнимой части комплексного параметра А от частоты, который в свою очередь зависит от электрофизических свойств частицы и сре- Рисунок 3 - Зависимости силы от частоты для двух частиц с разными свойствами Если направления чередования фаз потенциалов электродов двух частот противоположны, то в межэлектродной области возникают два встречно бегущих электрических поля. В этом случае формулы (9) и (10) принимают вид: F1 = F1 (») - F1 (»2);F2 = F2 (»1) — F2 (»2 ), (11) и тогда в соответствии с рисунком 3 при значениях го1 и го 2, которые соответствуют максимумам функций F1 (го) и F2(го), F1 >0, а F2<0. То есть силы направлены в противоположные стороны. Для решения уравнения движения в поле двух частот по формулам системы (8) коэффициент C3 находится по формуле Сз = F *( A(» ) - A» ))U2 6nqah3 ды (ос, ес, оч, еч). Если в жидкости находится вторая частица с другими свойствами, то на нее будет действовать сила F2 = F2 (»1) + F2 (»2 ), (10) которая определена другим видом зависимости мнимой части комплексного параметра А от частоты. На рисунке 3 построены зависимости величины силы от частоты для двух частиц с разными электрофизическими свойствами. На рисунке 4 показаны графики движения двух частиц с разными электрофизическими свойствами в бегущих электрических полях двух частот. Зависимости рисунка 4 построены для жидкости (подсолнечное масло) со следующими свойствами: ос = 10-9 См/м; ес = 3,240-9 Ф/м; П = 0,054 Па-с и частицы: a = 50 мк, р = 1300 кг/м3, размеров области: h = 2 мм; l/h = 0,5. Движение частиц начинается с точки с координатой Y = 0. Напряжение на электродах - 2 кВ. Из полученных закономерностей следует, что частицы за 100 с разойдутся на расстояние 110 мм и будут разделены по признакам электрофизических свойств. Теоретические исследования динамики частиц в двух бегущих полях разной частоты показывают возможность разделения их по признаку электрофизических свойств: диэлектрической проницаемости и удельной электропроводности. Причем на 81 процесс разделения влияет как напряжение на электродах, так и частота электрического поля. 1 – σч = 10-7 См/м; εч = 2,1∙10-11Ф/м; 2 – σч =4∙10-8 См/м; εч = 2,9∙10-11Ф/м Рисунок 4 – Зависимости Y-координаты частиц от времени Для подтверждения полученных результатов были проведены экспериментальные исследования по разделению частиц шрота подсолнечника разной влажности. Использовался шрот влажностью 6% и 14%, который добавлялся в рафинированное подсолнечное масло в равных долях. Содержание шрота каждой из фракций составляло 0,25%. Предварительно были определены электрофизические характеристики приготовленной суспензии по методике [6]. Частицы первой фракции имели удельную электропроводность 4,4∙10-8 См/м, а диэлектрическую проницаемость – 4,4∙10-8 Ф/м. Угловая частота, которая соот- ветствует максимальной силе, для этой фракции составляет 446 рад/с. Частицы второй фракции имели удельную электропроводность 4,3∙10-7 См/м, а диэлектрическую проницаемость – 7,2∙10-8 Ф/м. Угловая частота, которая соответствует максимальной силе, для этой фракции составляет 3215 рад/с. В экспериментальных исследованиях использовалась камера с двурядной системой электродов с h = 5 мм и l/h = 0,5. Длина камеры составляет 80 мм, поэтому для полного разделения фракций максимальное расстояние, которое должна преодолеть частица каждой фракции, составляет 80 мм. На электроды подавалось четырехфазное напряжение 7,2 кВ. теоретическая зависимость для первой фракции теоретическая зависимость для второй фракции экспериментальная зависимость для первой фракции Рисунок 5 – Динамика разделения шрота подсолнечника разной влажности Содержание шрота в масле определялось по ГОСТ 5481-89. Пробы масла отбирались через 200 с. Теоретические зависимости (рисунок 5) строились по формулам (8) и (12) с учетом гранулометрической характеристики шрота. Сравнение полученных экспериментальных результатов хорошо согласуется с теоретическими (рисунок 5). Расхождение не превышает 11%. Таким образом, теоретически обоснована и экспериментально подтверждена возможность разделения частиц суспензии с разными электрофизическими свойствами в поле двух встречно бегущих электрических полей, созданных многофазными системами электродов.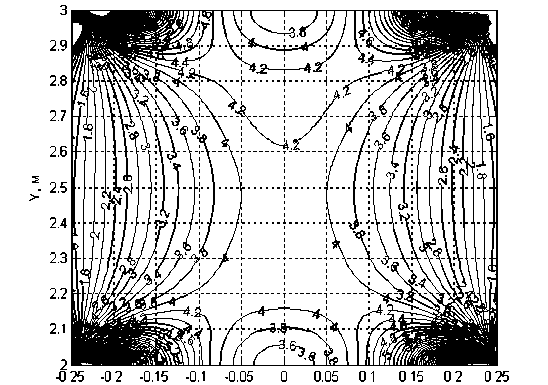
Список литературы Сепарация слабопроводящих суспензий в бегущем электрическом поле
- Украинцев, М.М. Электростатический фильтр для очистки подсолнечного масла/Е.И. Тимонина, М.М. Украинцев//Механизация и электрификация сельского хозяйства. -2001. -№ 11. -С. 26-28.
- Болога, М.К. Рафинация подсолнечного масла в электрическом поле: монография/М.К. Болога, И.И. Берилл; АН Республики Молдова, Институт прикладной физики. -Молдова: Stinta, 2004. -214 с.: ил.
- Пат. 94810 Україна, МПК В 01D35/6. Спосiбелектричної очистки дiелектричнихрiдин/I.П. Назаренко, В.А. Дiдур (Україна). -№ а 200911592; заявл. 13.11.2009; опубл. 10.06.2011, Бюл. № 11.
- Назаренко, I.П. Теоретичнi дослiдження взаємодiї електричного поля з дiелектричними суспензiями в багатоелектродних системах/I.П. Назаренко//Працi Таврiйського державного агротехнологiчного унiверситету: наук. фах. видання/ТДАТУ. -Мелiтополь, 2012. -Вип. 12. -Т. 1. -С. 35-45.
- Назаренко, I.П. Визначення електрофiзичних властивостей дiелектричних суспензiй/I.П. Назаренко, М.О. Рубцов//Працi Таврiйського державного агротехнологiчного унiверситету: наук. фах. видання/ТДАТУ. -Мелiтополь, 2011. -Вип. 11. -Т. 3. -С. 167-175.
- Назаренко, I.П. До питання визначення електрофiзичних властивостей дiелектричних суспензiй/I.П. Назаренко//Працi Таврiйського державного агротехнологiчного унiверситету. -Вип. 11. -Т. 4. -Мелiтополь, 2011. -С. 66-70.


