Сетевая модель данных службы каталогов

Служба, каталогов (Directory Service) — средство иерархического представления различных ресурсов и хранения информации об этих ресурсах. В качестве ресурсов выступают материальные ресурсы, персонал, сетевые ресурсы и т. д.

Информация об определенном объекте (ресурсе) хранится как значения атрибутов этого объекта.

Служба, каталогов в контексте компьютерных сетей — программный комплекс, позволяющий администратору работать с упорядоченным по ряду признаков массивом информации о сетевых ресурсах (общие папки, серверы печати, принтеры, пользователи и т. д.), хранящимся в едином месте, что обеспечивает централизованное управление как самими ресурсами, так и информацией о них, а. также позволяющий контролировать использование их третьими лицами.

OpenLDAP — это служба, каталогов, которая позволяет нам работать с различными сетевыми ресурсами (пользователями, компьютерами, принтерами, зонами DNS, а также всем, что необходимо вам для работы).

Вся работа, осуществляется по протоколу LDAP (англ. Lightweight Directory Access Protocol). Это сетевой протокол для доступа, к службе каталогов Х.500, разработанный IETF как облегчённый вариант ITU-T протокола. DAP. LDAP — относительно простой протокол, использующий TCP/IP и позволяющий производить операции авторизации (bind), поиска, (search) и сравнения (compare), а. также операции добавления, изменения или удаления записей.

Любая запись в каталоге LDAP состоит из одного или нескольких атрибутов и обладает уникальным именем (DN — англ. Distinguished Name). Уникальное имя состоит из одного или нескольких относительных уникальных имен, разделённых запятой. Относительное уникальное имя имеет вид «ИмяАтрибута=значение». На одном уровне каталога, не может существовать двух записей с одинаковыми относительными уникальными именами. Для хранения записей OpenLDAP использует базу данных Berkeley DB, но доступны различные модули для хранения данных в других БД.

Структуры хранения данных каталога

Стандартная структура хранения данннх каталога

Служба, каталога, как и большинство каталогов, имеет структуру организации хранения данных в виде ориентированного граф-дерева, (рис. 1), где у каждого «родителя» есть один «потомок». Данная структура детально описана в стандарте протокола RFC 4512 и использует иерархическую модель данных.

Такую структуру можно описать графом G = ( V, Е ), г де V (G) — множество вершин графа V (G) = (г/,г_р,го,. ..фі), E(G) — множество дуг графа , Е(G) = ({г/,г_р},{г_р,го},..,,{г_р,гД).

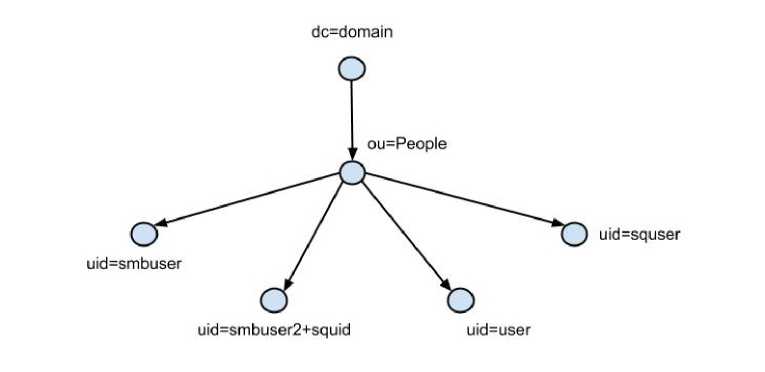
Рис. 1. Пример стандартного дерева, каталога.

Вершины обозначаются согласно принадлежности к типу записи:

Dd — вершина корневого элемента de,

Гр — вершина-родитель для группы записей (ou=People),

Di — вершина-потомок для записи в каталоге,например, uid=smbuser, г — количество записей, г = 1... п

Поиск записей в таком графе осуществляется по всему дереву службы каталогов, таким образом время поиска каждой записи будет прямо пропорционально зависеть от общего числа, записей каталога. Чаще всего при настройке каталога, и сервисов взаимодействующих с ним выбирают одну ветку для хранения и поиска, записей — ou=People. В таком случае время ответа на запрос к каталогу будет связан с содержанием ветки ou=People, а именно количеством записей в ней. Данная особенность связана со способом хранения и получения информации в Berkeley DB, которая используется по умолчанию в службе каталогов OpenLDAP.

Сетевая модель данных структуры каталога

Современная версия клиентской и серверной частей LDAP, описанная в RFC 4511, позволяет хранить, записывать, осуществлять поиск записи в разных ветках каталога, а. сервисам-службам — работать с ними. Группируя записи по их общим параметрам (атрибутам и объектным классам, используемым сервисам), можно построить более упорядоченную структуру хранения данных. Более того, отслеживая изменения в активности сервисов, можно организовать адаптивную службу каталогов, меняющую свою структуру в зависимости от динамики запросов к ней.

Но следует учитывать тот факт, что для начальной поддержки работоспособности всех сервисов существует необходимость хранения записей или ссылочных записей («алиасов») в ветке ou=People.

Таким образом, можно сформировать новую структуру каталога, использующую уже сетевую модель данных (рис. 2).

Рассмотрим такую структуру хранения данных службы каталогов с корневым элементом dc=domain, в которой записи сгруппированы по используемым сервисам-службам. С данным каталогом работают два. сервиса: файловый сервер (ветка. ou=Samba) и проксисервер (ветка ou=Squid). Как видно из рисунка, записи, используемые только одним каким-то сервисом, хранятся в соответствующей ему ветке (ou=Samba,dc=domain и ou=Squid,dc=domain), а для записей, используемых в обоих сервисах, используется специальная запись alias.

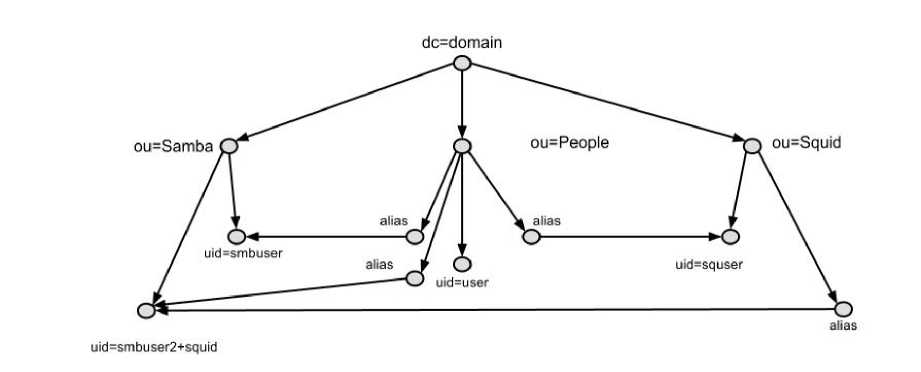
Рис. 2. Предлагаемая структура, храпения данных

Предлагаемая структура. хранения данных является ориентированным граф-деревом G“‘ = (V “‘,Е “‘), где V “‘(G“‘) — множество вершин графа V “‘(G“‘)=^t)d, v_p Vo,-• •№ dWtr ,.,vaj ^o_0v ^^>o_s\ Е “‘(G^) — множество дуг графа, дуги которого различны для каждого отделвного каталога, и имеет несколько родительских вершин (ou=Samba,ou=Squid,alias) для вершины-потомков (uid=smbuser,uid=smbuser2+squid,uid=squid), где

Vd ~ вершина корневого элемента de.

v _p — вершина-родитель для группы записей (ou=People),

Vt — вершина-потомок для записи в каталоге, например, uid=smbuser, vcj — вершины-ссылки, они же alias, vos — вершины-службы, г — количество 'записей, г = 1... п.

j — количество записей-ссылок, s — количество сервисов, работающих с каталогом.

Методика поиска принадлежности вершин

Для построения предлагаемой структуры каталога, необходимо учитывать критерии необходимости перемещения записи в графе.

Процесс определения вершин, требующих перестроения в дереве каталога, можно разделить на. несколько этапов:

• 1.    определение используемых сервисов;

• 2.    определение важности того или иного сервиса;

• 3.    определение используемых атрибутов и объектных классов;

• 4.    группирование записей по важности сервиса, и используемым атрибутам.

Для определения используемых сервисов прежде всего следует определиться с набором ролей сервера. Например, для роли файлового сервера, используется сервис samba.

Чаще всего используют такое соответствие:

• -    файловый сервер — сервис samba;

• -    прокси-сервер — сервис squid;

• -    почтовый сервер — сервисы postfix и dovecot;

• -    сервер аутентификации — РАМ.

Данное соответствие позволит четко определить вид записей в каталоге.

Например:

dn: uid=user,ou=People,dc=example,dc=com

givenName: user sn: user cn: user user sambaAcctFlags: [UD ]

mgrpDeliverTo: user objectClass: top objectClass: person objectClass: organizationalPerson objectClass: inetorgperson objectClass: posixAccount objectClass: mailgroup objectClass: sambaSamAccount uidNumber: 10022

gidNumber: 10022

homeDirectory: /home/user loginShell: /bin/bash sambaSID: S-l-5-21-2098741869-3465982337-3637863451-10022

sambaNTPassword: EE42945FD699570D2DA4C2A0BE29D3B5

sambaLMPassword: 8131BC5135B26C62C81667E9D738C5D9

sambaPasswordHistory: 00000000000000000000000000000000000000000000000000000000 00000000

sambaPwdLastSet: 1362051479

userPassword::

elNTSEF9R0tPSmclaFd5Z09JWVJBYVY3MGx3QURjTnhNZUxpSmxTVHFtRkE9PQ= uid: user

Каждый сервис имеет свои специфические свойства:

• -    количество необходимых атрибутов,

• -    вид работы (чтение/запись на жесткий диск или иной носитель данных, запросы поиска к СУБД).

Раннее проведенный анализ работы службы каталогов OpenLDAP с набором таких сервисов, как почтовый сервер, прокси-сервер, файловый сервер и сервер аутентификации показал, что больше всего времени для ответа на запрос необходимо файловому серверу, так как требуется наибольшее количество атрибутов и объектных классов, чтение данных и запись на диск, затем идут почтовый и прокси-серверы, и сервер аутентификации требует меньше всего времени ответа на запрос.

Касательно загруженности системы данный порядок сохраняется.

Имея эти данные, можно определить «числовые критерии сервисов» из условия, что наименьшее число — это наиболее критичный сервис.

Таким образом, имеем:

• -    файловый сервер — критерий равен 1;

• -    почтовый сервер — 2;

• -    прокси-сервер — 3;

• -    сервер аутентификации — 4.

• Д анные загруженности по сервисам представлены в табл. 1.

Так как каждый атрибут связан с определенным классом или группой классов, несложно определить частоту использования того или иного сервиса для различных операций с каталогом (чтение, изменение, удаление). Для определения точного множества необходимых атрибутов и классов удобно воспользоваться табл. 2 «Атрибуты для различных сервисов» и формулой 1, полученными в более ранних исследованиях.

Для точного определения необходимых атрибутов удобно воспользоваться формулой (3):

С = ((B _i \B _i+1) ...(B _n-₁ \B _n ))(B _n \((B _i \B _i+1 )...(B _n- i \B _n ))),               (1)

Таблица!

Нагруженность системы при различный сервисах

Сервис	Аутентификация bdb	Добавление пользователя bdb	Удаление пользователя bdb	Отправка почты bdb	Прием почты bdb
squid	CPU-70%,ФС-70%	_	_	_	_
samba (smbldap-tools)	CPU-84%,ФС-92%	CPU- 86%,ФС-100%	CPU- 79%,ФС-100%	_	_
postfix + dovecot	CPU-73%,ФС-69%	_	_	CPU- 73%,ФС-72%	CPU- 73%,ФС-75%
pam	CPU-71%,ФС-71%	_	_	_	_
postfix + courierimap	CPU-75%,ФС-70%	_	_	CPU- 77%,ФС-75%	CPU- 74%, ФС-78%

Т а б л и ц а 2

Атрибуты для различных сервисов

Файловый сервер (атрибуты) Критерий Почтовый сервер (атрибуты) Критерий Проксисервер (атрибуты) Критерий Сервер аутентификации (атрибуты) Критерий uid uidNumber gidNumber homeDirectory СП sn description displayName objectClass modifyTimestamp Samba* userPassword loginShell gecos shadowMax memberUid 1 uid uidNumber gidNumber homeDirectory userPassword mail 2 uid userPassword 3 uid userPassword uidNumber gidNumber homeDirectory cn loginShell gecos description objectClass 4 где г = 1... п, п — количество сервисов,

B i — множество атрибутов для определенного сервиса,

С — уникальное множество атрибутов.

Таким образом, выделяются множества атрибутов и классов, необходимых для работы сервисов.

По полученным данным заполняются табл. 3 «Записи сервисов» и табл. 4 «Записи каталога с учетом критерия сервиса», из которых принимается решение о переносе вершины записи в одну или другую ветку каталога.

Т а б л и ц а 3

Записи сервисов

запись	атрибут	класс атрибута	частота появ ления атрибута	сервис, который запрашивал атрибут

Т а б л и ц а 4

Записи каталога с учетом критерия сервиса

запись	сервис	частота использования сервиса	критерий сервиса

Построение сетевой модели данных структуры каталога

Определив раннее множество вершин V‘г, требующих перестроения, можно для каждой записи Di построить граф новых связей G‘i=(V‘гYEYY

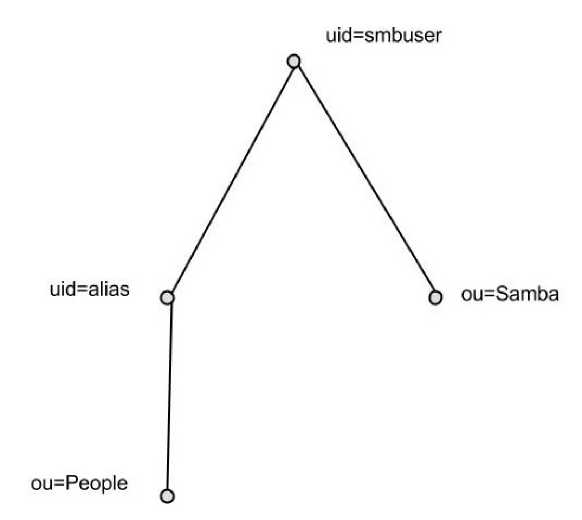
Рис. 3. Дополнительные подграфы вершин

Выделив вершины v‘i, строится граф с и сходной вершиной v‘i, вершинами «алиасов» va j и вершиной-родителем групп voo, вершинами-родителями для «алиасов» v_p, voi,.^oj—-!.

Следует отметить, что «алиасов» у записи может быть несколько, соответственно у каждого «алиаса» будет своя вершина-родитель ( vo j-Д но у каждой записи будет «алиас» для вершины v_p.

N — количество вершин-записей в каталоге, j = 1... т, т — количество «алиасов» для записи или количество веток, в которых хранится запись.

Добавление дуг сервисов к исходному графу

Для того чтобы связать полученные графы вершин и основное дерево каталога, добавим к исходному графу G дуги E j (G“)“ = (vd,voc,...,voj-i) и вершины V-(G“)“= ({vd,voc}, ..., {vd,voj—1}), задающие новые ветки.

Объединив множества вершин и дуг, получим новый граф G“(E“, V“):

V “ = V UV “i

Е “ = Е U Е “

G“ = (E “,V “)

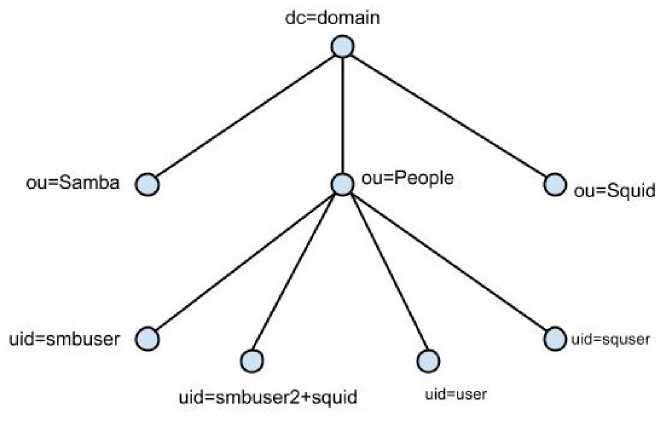
Рис. 4. Дополнительные дуги

Удаление дублирующихся записей-вершин

Перед объединением графа G‘ - и основного графа G необходимо удалить дублирующиеся записи-вершины v- для v‘- и дуги {v-,vp} в ветке ou=People.

Удаление вершины. Пусть G = (Е, V ) — граф и v Е V. Удалить вершину v из графа G — это значит построить новый граф G“ = (Е “, V“), в котором V“ = V\{v} и Е“ получается из Е удалением всех ребер, шшидептпых вершине v.

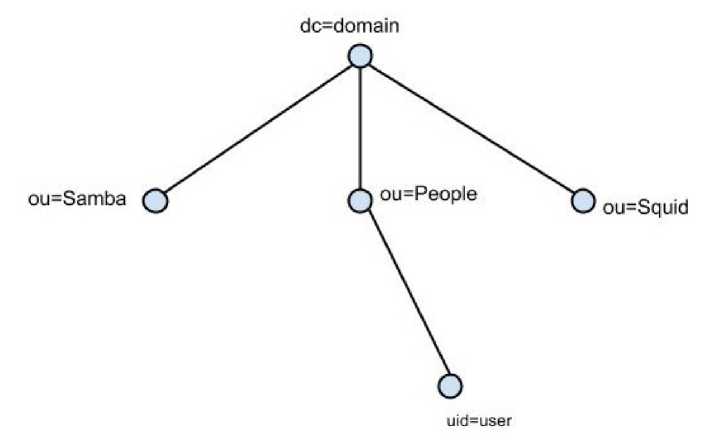
Рис. 5. Удаление дублирующихся вершин

Объединение графов

Графы вершин G ^ для каждых вершин V объединяются с графами G’”:

V “ = V “ U V ‘І,

Е “ = Е “ U Е\,

G“‘ = (Е “,V “‘).

В резулвтате чего получим новую структуру каталога, использующую сетевую модель данных, изображенную на рис. 2.

Модифицированный алгоритм поиска наименьшего пути Дейкстры

Для сравнительного анализа иерархической модели данных и сетевой воспользуемся модифицированным алгоритмом поиска наименьшего пути Дейкстры, который учитывает специфику службы каталогов.

Для поиска кратчайшего пути в дереве каталога необходимо ввести определение веса перехода а, которое будет использоваться далее.

а — некоторое число, определяющее затраты, такт перехода из одной вершины в другую.

Также введем следующие обозначения:

s — начальная вершина, t — конечная вершина, ж — текущая вершина.

Положим для начальной вершины a(s) = 0. Вес первой дуги из вершины s в ж a(s, жД = = 1. Тогда для любой другой вершины с учетом механизма поиска в службах каталогов

а(s,Ж г ) = 1 + a(s,Жj_-1),                                      (2)

где 1 — вес первой дуги,

a(s, ж^-Д — вес дуги для вершины ж^-ъ

Алгоритм поиска наименьшего пути:

Шаг 1. Перед началом выполнения алгоритма все вершины и дуги не окрашены. Каждой вершине ж присваивается некое число гі(ж), равное длине кратчайшего пути из вершины-источника s в ж, включая все вершины, ранее записанные в службу каталогов.

Следует отметить тот факт, что поиск в каталоге происходит перебором всех записей, последовательно записанных в определенную ветку.

Соответственно d(s) = 0, a d(x) = то для всех вершин, отличных от вершины-источника s. Вершину s окрашиваем и временной переменной у присваиваем s (у = s). у — последняя окрашенная вершина.

Вершина-источник — это вершина, заданная при поиске, чаще всего ou=People.

Шаг 2. Для каждой неокрашенной вершины x следующим образом пересчитать величину d(x):

d(x) = min{d(x), d(y)} + a(y, x).                              (3)

Если d(x) = то для всех вершин x, такого пути нет. В противном случае окрасить ту вершину х, для которой величина d(x) является наименьшей. Также окрасить дугу, ведущую в выбранную на данном шаге вершину х. Меняем значение у = х.

Для современных служб каталогов величина d(x^) будет равна величине веса дуги вершины Xi, так как во время перехода по графу будут закрашены все дуги и вершины, записанные раннее в текущей ветке каталога:

d(x _i ) = a(s,x _i ) =Е^ a(s,x _t ),                                 (4)

где N — количество вершин в поиске.

Шаг 3. Если у = t (конечная вершина поиска), закончить процедуру. Кратчайший путь из вершины s в t найден. Иначе перейти к шагу 2.

Рассмотрим стандартную структуру каталога, изображенную на рис. 1.

В данной случае s — это вершина ou=people, t — вершина uid=squser.

Определим веса дуг, согласно формуле 2:

a(people, smbuser) = 1

a(people, smbuser + squid) = 1 + a(people, smbuser) = 2

a(people, user) = 1 + a(people, smbuser + squid) = 3

a(people,squser) = l+a(people,user)=4 a(people, squser) = 1 + a(people,user) = 4

Согласно формуле (4) d(squser) = 4

Таким образом, кратчайший путь для вершины uid=squser будет самым длинным по сравнению с другими вершинами графа.

Рассмотрим предлагаемую структуру каталога, изображенную на рис. 2.

В предлагаемой структуре каталога — графе — поиск уже ведется от специально созданной вершины ou=Squid.

Для неё определим веса дуг:

a(squid, squser) = 1

Величина d(squser) = 1.

В данном случае путь до вершины uid=squser будет короче, чем при стандартном графе. При таком построение графа поиск записи будет осуществляться быстрее.

Заключение

Предлагаемая структура хранения данных требует в дальнейшем более детального изучения. В данном представлении сетевая модель является избыточной из-за дублирования записей в ветке ou=People, что приведет к большим затратам для хранения данных на жестком диске. Но для основной задачи — минимизации времени ответов на запросы — является предпочтительней стандартной, иерархической.

В дальнейшем следует также рассмотреть возможность изменения структуры каталога в зависимости от периодической загрузки каталога, т.е. такой случай, когда определенные ветки каталога хранить на разных носителях данных в зависимости от важности ресурса.