Сетевая модель межотраслевого баланса производства продукции горной промышленности

При росте сложности систем, специализации и разделении труда возрастает роль анализа структуры связей при проектировании, управлении, обеспечении безопасности технических, экономических систем. Например, в карьерах, шахтах возникают или закрываются пути добычи и транспортировки продукции, меняются системы энергоснабжения, вентиляции, связи между местами добычи, обогащения, переработки, и т.д. Необходим расчет поведения сложных систем при изменении структуры связей элементов, включая изменение хозяйственных связей между участниками процесса производства. Расчет таких задач всегда был проблемой больших данных, в том отношении, что расчет реальных задач превышал по времени потребности управления. Сетевая модель межотраслевого баланса системы промышленного производства представляет как процесс производства продукции, так и структуру хозяйственных связей. Основанный на сетевой модели алгоритм обеспечивает расчет изменения производства при изменении структуры хозяйственных связей, включая расчет по частям для ускорения вычислений.

2.    Тензорный метод двойственных сетей

Математической основой исследования сетевых моделей сложных систем при изменении структуры является тензорный метод, разработанный в работах Г. Крона [1], А. Петрова [2, 3], других ученых [4, 5, 6]. Сама система, и протекающие в ней процессы, рассматриваются как тензор, а состояния системы для разных структур – как проекции в разные системы координат. Переход от одной структуры связей к другой структуре производится как преобразование координат, и может быть автоматизирован.

Тензорный метод двойственных сетей обеспечивает создание сетевых моделей на основе аналогий процессов и структуры. Данный метод основан на инварианте двойственности при изменении структуры. При изменении соединения элементов постоянна сумма метрических тензоров двух сетей с двойственной структурой. Этому соответствует постоянство суммы рассеиваемых мощностей двух двойственных электрических цепей при изменении структуры соединения их ветвей. Сетевые модели сложных систем обеспечивают расчет изменения процессов при изменении структуры, включая декомпозицию на подсистемы и расчет по частям, что снижает объемы вычислений.

Модели сложных систем используют аналоги между исследуемой системой и сетью для представления одновременно структуры и процессов в структуре, которые меняются при изменении структуры по тензорным законам. Созданы сетевые модели для расчета технических систем [1, 2], межотраслевого баланса [2, 7], систем коммуникации [5], линейного программирования [6], систем управления [8, 9], а также сетевые модели физических систем.

В данной статье для решения задачи межотраслевого баланса рассмотрена сетевая модель потоков продуктов. Данная модель обеспечивает расчет объемов производства для обеспечения спроса и поставок; потребления необходимых ресурсов и комплектующих; проектирование и анализ работы промышленности при реструктуризации, изменении хозяйственных связей. Представленный алгоритм расчета по частям задач баланса большой размерности позволяет разделять сетевую модель рассматриваемой системы производства на части и применять параллельные вычисления. Это уменьшает объемы вычислений за счет обращения матриц меньшего порядка, что позволяет повысить оперативность управления.

Сетевая модель системы производства представлена эквивалентной электрической цепью [2]. Аналогии продуктов и сети используют двойственные источники в замкнутых путях. Двойственные отклики замкнутых и разомкнутых путей в совокупности представляют сумму компонентов – потоков продуктов в отраслях.

3.    Сетевая модель межотраслевого баланса

Данная задача известна как модель «затраты – выпуск». Задана система отраслей (производств), связи между отраслями и нормы взаимного потребления продукции, спрос. Необходим расчет производства продукции, которая обеспечивает спрос, поставки и потребление ресурсов. Отрасли производят продукцию в количестве, определяемом спросом рынка (заданным планом). Часть продукции поставляют другим отраслям. Сами отрасли потребляют поставки других отраслей, ресурсы, энергию, труд, необходимые для производства продукции. При ограничении определенных ресурсов, необходимо оптимизировать выпуск, или обеспечить выпуск продукции приоритетных отраслей и т.д.

Модель межотраслевого баланса исследована в работах В. Леонтьева [10], В. Косова [11], других авторов [12, 13]. Отмечалось, что проблема расчета объединенного материального и финансового баланса не решена.

В период Второй мировой войны Леонтьев разработал матрицу «затраты — выпуск» для экономики Германии; результаты использовались для выбора целей бомбардировки. Аналогичный баланс для СССР власти США использовали для принятия решений об объёмах и структуре поставок по ленд-лизу.

Расчеты балансов применяются для управления производством на государственном уровне, а также отраслями и предприятиями. Расчет межотраслевого баланса (МОБ) в настоящее время осуществляет Росстат. Универсальность задачи баланса такова, что в качестве «отраслей» можно рассматривать предприятия, технологические линии, страны, регионы. Существуют балансы в натуральном и денежном выражении. Двум видам межотраслевого баланса: материальному балансу и финансовому балансу соответствуют две двойственные по своей структуре сети.

Для добычи и производства руды, угля, углеводородов, продуктов первичной обработки необходим расчет потребления поставок и ресурсов (машин и механизмов, электроэнергии, ГСМ, транспорта, воды, работников, и др.). Для обеспечения работы горных предприятий необходимы поставки продукции других отраслей (машиностроения, электроэнергии, транспорта, химии, АПК, и т.д.). Ресурсы и необходимые поставки других отраслей на входе предприятий обеспечивают на выходе выпуск продукции предприятий горной промышленности, объемы которой заданы платежеспособным спросом.

Сетевая модель межотраслевого баланса позволяет по заданному спросу (плану) рассчитать потоки ресурсов, производства продукции. Модель дает наглядное представление хозяйственных связей при добыче угля, руды, процессов транспортировки и обогащения. Разделение задачи на части обеспечивает ускорение расчетов, а также дает возможности анализа товарных и денежных потоков. Сетевая модель применяется для расчета межотраслевого баланса страны, отраслей, а также для оценки натуральной стоимости и базовой цены месторождений [14], размещения и распределения ресурсов [15].

Расчеты задач планирования, включая межотраслевые балансы, всегда были связаны с проблемой больших данных. Времена расчетов реальных данных с сотнями, тысячами отраслей и предприятий превышают плановый период. Это не обеспечивает возможности анализа различных вариантов с целью поиска оптимального решения, снижает эффективность управления производством. Размерности задачи, в зависимости от степени детализации, составляют десятки тысяч показателей.

Для решения данной проблемы разработана сетевая модель межотраслевого баланса производства, которая при декомпозиции сети на части с применением параллельных вычислений обеспечивает ускорение расчетов.

Математическая постановка задачи имеет вид уравнений потоков продуктов. Система хозяйства состоит из n отраслей с валовым выпуском продукции X i (где i = 1, ..., n ), для обеспечения спроса y i и поставок x ij . Отрасли потребляют ресурсы и поставки. На выходе отраслей это представляет система уравнений распределения валового выпуска [10, 11, 2]:

X = A X + Y ,                                 (1)

Поставки между отраслями определяют коэффициенты прямых затрат a ij (КПЗ). Матрица КПЗ обозначается A . Значения КПЗ численно равны количеству продукта отрасли i , которое необходимо для производства единицы продукта отрасли j. Росстат рассчитывает затраты одного продукта на производство другого продукта (например, расход электроэнергии на производство угля) в рублях на 1000 рублей продукции.

Значения поставок продуктов x ij между отраслями выражаются уравнением:

x ij = a ij X j .                                                             (2)

Потребление ресурсов r ki определяет коэффициенты затрат ресурсов b kj , которые равны количеству ресурса k для производства единицы продукта отрасли j, или в рублях на 1000 рублей продукции:

r ki = b ki X i .                                                        (3)

Данные коэффициенты устанавливают пропорции между воздействием, валовым выпуском, и откликом, потоком поставки или ресурса. Они определяют нормы потребления поставок и ресурсов при производстве продукции; могут оставаться постоянными на протяжении определенного периода, но меняются по мере совершенствования технологий.

Валовые выпуски из соотношения (1), путем обращения матрицы:

X = (I – A)^-1 Y                                               (4)

Здесь I – единичная матрица, а сама ( I – A ) называется экономической матрицей. В реальных задачах порядок этой матрицы может иметь столь большие значения, что время обращения превышает потребности для управления производством.

Коэффициенты прямых затрат меньше единицы, а в реальных задачах много меньше единицы поэтому норма матрицы A меньше единицы. Тогда обратную экономическую матрицу можно разложить в степенной ряд:

(I – A)^–1 = I + A + A² + A³ + ... (5)

Элементы обратной экономической матрицы – это коэффициенты полных затрат, которые учитывают затраты, связанные с производством продукта не только прямо, но и косвенно через другие продукты, участвующие в производстве данного продукта. Например: для определения полных затрат металла на производство станков надо учитывать затраты на производство руды, чугуна, электроэнергии на выплавку стали, обработку металлов и производство других материалов, из которых изготавливаются станки; на выработку топлива для производства металла; на транспортировку всех необходимых материалов с мест производства до предприятий-потребителей, т.е., по всей цепи технологических связей.

В системах отчетности составляется симметричная таблица «затраты–выпуск», в ней связываются продукты с продуктами, отрасли с продуктами, учитываются взимаемые налоги. Для международного информационного обмена применяется ССРД МВФ – Специальный стандарт распространения данных Международного валютного фонда, к которому Россия присоединилась в 1997 г. Таблицы «затраты–выпуск» применяются для расчета прогнозов и различных сценариев развития производства, например, выпуска продукции горных отраслей.

В информационном отношении межотраслевой баланс при решении реальных задач требует больших объемов вычислений, что всегда было проблемой больших данных. Степенной ряд (5) сходится медленно. Время расчета экономической матрицы для задачи в тысячи показателей превышает плановый период. Для реальных задач планирования число показателей может составлять миллионы, что из-за большого времени расчетов затрудняет их применение для управления и прогнозирования. Декомпозиция и расчет по частям сокращает время расчетов, позволяя управлять изменениями в реальном времени.

Для разделения системы производства на подсистемы и расчета по частям разработана сетевая модель межотраслевого баланса. Расчет объемов производства при разделении сетевой модели на части обеспечивает снижение времени вычислений. Расчеты можно проводить с применением параллельных вычислений.

В сетевой модели описаны все соотношения между потоками в системе. Это позволяет привести уравнения поведения к тензорному виду. Тогда при изменении координат (структуры связей) потоки продуктов производства, поставок, ресурсов преобразуются по линейным законам. Это позволяет преобразовать решение старой сети в решения измененных связей. Баланс потоков продуктов на выходе отраслей аналогичен балансу токов в узлах электрической цепи. Баланс между потоками на входе отраслей имеет вид:

I a ij + X b kj = 1 .                                               (6)

Это условие (для выпуска продукта нужны все поставки и ресурсы) обычно не используют, однако оно дополняет описание потоков в сетевой модели. Отметим, что сумма потоков спроса на выходе равна сумме потоков ресурсов на входе: X r ik = X y i .

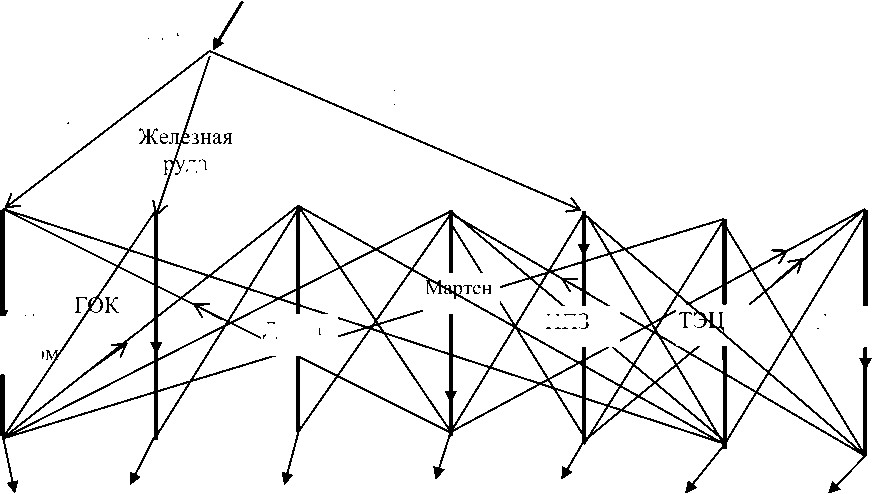
В качестве примера на рис. 1 представлены отрасли (вертикальные линии), которые обеспечивают производство продукции горной промышленности. Отрасли связаны взаимными поставками (наклонные линии). Сверху поступают добываемые природные ресурсы (уголь, железная руда, углеводороды). Стрелки внизу показывают воздействие на систему производства спроса (плана). Эта схема отражает естественную структуру процессов производства во взаимно связанных отраслях экономической системы. Представлены отрасли системы производства горной промышленности. Например, добыча руды, угля, углеводородов, горно-обогатительная, литейная, транспортная. Также в производстве необходимо использовать машиностроение, электроэнергию, воду, природный газ, которые в классификаторе по ССРД МВФ объединены в одну отрасль.

ПРИРОДА

Нефть, газ

Уголь

да

НПЗ

Домна

X 7

Чугун

Сталь

Полуфабрикат

ГСМ                 Транспорт

Электроэнергия

Рис. 1. Структура отраслей производства горной промышленности

X ₁

Углепро

Автопром

Антрацит

Вертикальные линии – это отрасли производства, потоки в них направлены вниз, от входов к выходам. Сверху к ним поступают ресурсы (уголь, железная руда и углеводороды).

Тонкие линии от выходов одних отраслей к входам других – это направления межотраслевых поставок. Стрелки внизу показывают рыночный спрос на продукцию отраслей (план производства), сверх потребностей данного кластера. Структура потоков продуктов задана технологиями, физическим содержанием процессов преобразования потоков материи и энергии при производстве обогащенной руды, антрацита, полуфабрикатов.

Пример экономической матрицы ( I – A ) для отраслей на рисунке 1:

1			2	3	4	5	6	7
	1	1	-0,2	-0,1	-0,1	0	-0,2	0
	2	0	1	-0,4	0	0	0	0
( I – A ) =	3	0	0	1	-0,4	0	0	0
	4	-0,1	0	-0,1	1	-0,1	0	-0,2
	5	0	0	0	-0,1	1	-0,2	-0,3
	6	-0,1	0	-0,2	-0,2	-0,1	1	-0,1
	7	0	0	0	-0,1	-0,1	-0,2	1

Двойные линии выделяют матрицы подсетей, на которые будет разделена система. Сетевая модель обеспечивает расчет при изменении структуры связей, появлении новых отраслей, ликвидации старых отраслей.

Значения спроса на продукцию зададим для этих отраслей вектором, например:

1           2           3           4           5           6           7

Y i =        300       300       400       500       200       200       100

Проведем расчет по частям сети на рис. 1. Для этого разделим сеть на подсети, рассчитаем их, а затем соединим решения подсетей, используя сеть соединения, в решение полной сети. Алгоритм расчета по частям состоит в следующем:

• 1.    Для разделения на части выделяем вдоль диагонали матрицы (I – A) подматрицы, размера подсетей. Выделенные блоки обращаем независимо, возможно параллельно.

• 2.    Сеть соединения. Ненулевые элементы, не попавшие в блоки подсетей, показывают связи между подсетями. Собрав ненулевые элементы вне блоков вместе с элементами на главной диагонали, получим матрицу сети соединения. Полученная матрица задает сеть соединения (пересечения отраслей), которая состоит из разорванных поставок и отраслей, которые связывают эти поставки.

• 3.    Расчет подсетей – обращаем их матрицы, получаем валовые выпуски отраслей.

• 4.    Расчет взаимодействия подсетей через сеть соединения. Для этого получаем воздействия подсетей на сеть соединения. Это валовые выпуски подсетей в отраслях, входящих в сеть соединения.

• 5.    Расчет сети соединения с воздействиями от подсетей. Обращаем матрицу сети соединения. Получаем валовые выпуски в отраслях сети соединения.

• 6.    Расчет обратного воздействия сети соединения на подсети. Обратные воздействия на подсети равны разности выпусков в сети соединения и воздействия со стороны подсистем. Это определяет взаимодействие подсетей, прирост потоков продуктов.

• 7.    Расчет подсетей с обратными воздействиями. Полученные результаты задают новые воздействия подсетей на сеть соединений, если требуемая точность не достигнута.

• 8.    Полный выпуск равен сумме выпуска в подсетях и приращений выпусков от сети соединения (или сумме всех значений предыдущих этапов и приращения выпуска от очередного этапа).

• 9.    Проверка точности решения. Вычисления по этапам повторяется, пока приращения не станут меньше заданного порога. Результат является решением задачи межотраслевого баланса.

• 10.    Если требуемая точность не достигнута, то выполняются следующие итерации.

• 11.    Получить приращения выпусков, которые станут новыми воздействиями подсетей на сеть соединений, и повторить этапы 4–8.

• 12.    Когда точность достигнута, получить значения потоков поставок и ресурсов; проверить баланс потоков в узлах входа и выхода отраслей.

Итерационный процесс сходится в силу того, что в процессе расчета нормы всех экономических матриц меньше единицы. Расчет небольших подсистем требует меньшего объема вычислений, чем обращение полной матрицы, что повышает эффективность. Результатом являются объемы валовых выпусков, поставок и ресурсов, которые представляют собой решение задачи межотраслевого баланса. Тестовые расчеты показали, что время расчета снижается тем сильнее, чем меньше плотность заполнения матрицы.

Разделим систему на рисунке 1 между отраслями 3 и 4. Этому соответствует выделение в экономической матрице двух подматриц вдоль главной диагонали, которые обведены двойной линией. Получим экономические матрицы двух подсетей и сети соединений.

Подсеть 1                    Подсеть 2                 Сеть соединения

	1	2	3	4		5	6	7	1		3	4	6
1	1,0	-0,2	-0,1	4	1,0	-0,1	0,0	-0,2	1	1,0	0,0	-0,1	-0,2
2	0,0	1,0	-0,4	5	-0,1	1,0	-0,2	-0,3	3	0,0	1,0	-0,4	0,0
3	0,0	0,0	1,0	6	-0,2	-0,1	1,0	-0,1	4	-0,1	-0,1	1,0	0,0
				7	-0,1	-0,1	-0,2	1,0	6	-0,1	-0,2	0,0	1,0

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

Соответствующие обратные экономические матрицы для двух подсетей и соединений имеют вид следующий: 1      2      3                     4      5      6      7                 1      3      4      6 сети 1 1,00 0,20 0,18 4 1,06 0,14 0,08 0,26 1 1,03 0,05 0,12 0,21 2 0,00 1,00 0,40 5 0,21 1,09 0,30 0,40 3 0,04 1,04 0,42 0,01 3 0,00 0,00 1,00 6 0,25 0,15 1,07 0,20 4 0,11 0,11 1,05 0,02 7 0,18 0,15 0,25 1,11 6 0,11 0,21 0,10 1,02 В сети соединений в качестве воздействий (спроса) на входе отраслей рассматриваются результаты расчета подсетей, т.е. выпуски в контактирующих с ними отраслях. В подсетях в качестве воздействий (спроса) на входе отраслей, при расчете обратного воздействия, рассматриваются приращения выпусков в соответствующих отраслях сети пересечений.

В таблице 1 представлены результаты расчета рассмотренного примера как целой, неразделенной системы, а также по частям, при разделении ее на две подсистемы, состоящие из отраслей 1-3, и 4-7. Полученные результаты для целой сети, а также подсетей на этапе 1, этапе 2 и отклонения от потоков выпуска продукции при расчете системы как целого, имеют следующие значения:

Таблица 1. Результаты расчета

Отрасли	Спрос (план)	Расчет целой сети	Расчет по частям			Отклонение
			Расчет подсетей	Сумма после этапа 1	Сумма после двух этапов	после первого этапа	после двух этапов
1	300	693,18	432,0	675,60	692,26	17,59	0,92
2	300	582,03	460,0	576,75	581,77	5,29	0,26
3	400	705,08	400,0	691,86	704,43	13,22	0,65
4	500	762,71	598,17	753,13	762,27	9,58	0,44
5	200	513,56	421,76	508,94	513,34	4,61	0,21
6	200	649,99	389,81	637,57	649,42	12,42	0,58
7	100	357,63	279,95	353,72	357,44	3,90	0,18

Полученные при расчете по частям потоки продуктов после второго этапа имеют незначительные отклонения от результатов расчета системы отраслей как целого.

Значения потоков поставок и ресурсов после завершения расчета по частям получаются по формулам (2) и (3). Эти потоки соответствуют потокам продуктов в полной, заданной сети, и являются решением задачи расчета межотраслевого баланса системы из 7 отраслей по частям.

Если есть собственное потребление отраслями своей продукции, то это необходимо учитывать при расчете. Тогда все отрасли, которые потребляют свою продукцию (например, электроэнергетика), следует представлять двумя ветвями. Одна ветвь от входа к выходу, как и ранее, представляет процесс производства. Другая ветвь, от выхода к входу, представляет процесс потребления. Получается цикл в каждой такой отрасли.

4.    Обсуждение результатов

Применение сетевой модели межотраслевого баланса обеспечивает наглядное представление структуры хозяйственных связей. Это позволяет проводить декомпозицию системы и расчет по частям, что снижает объемы вычислений, ускоряет плановые расчеты. В рассмотренном примере вместо обращения матрицы седьмого порядка, обращаются две матрицы четвертого порядка и одна матрица третьего порядка. Достаточно высокая точность расчета достигается уже на втором этапе вычислений. Следует отметить, что в экономическую матрицу включены два коэффициента прямых затрат, равные 0,4, что ухудшает так называемую обусловленность матрицы и ее время ее обращения. В реальных задачах значения этих коэффициентов много меньше единицы. При решении реальных задач, в которые входят сотни и тысячи предприятий экономия вычислений многократно выше, чем в демонстрационном примере. Это не только снижает объемы вычислений, повышает оперативность управлением системами производства. Сетевая модель позволяет анализировать различные варианты изменения хозяйственных связей, которые возникают и исчезают при создании новых или закрытии устаревших производств, технологий, появлении или закрытии рынков сбыта, и т.д.

5.    Предложения по направлению будущих исследований

Развивать сетевую модель системы производства по аналогии с двойственной электрической цепью [2] с целью создания аналитического инструмента для анализа потоков продуктов и потоков денежных средств на предприятиях горной промышленности. Аналогии продуктов и сети используют двойственные источники токов в открытых путях и источники напряжения в замкнутых путях. Двойственные отклики замкнутых и разомкнутых путей в совокупности представляют потоки продуктов в отраслях. Потоки в двойственной сети могут представлять пропорции в распределении денежных средств.

6.    Заключение

Таким образом, построение сетевой модели межотраслевого баланса позволяет представить систему предприятий горной промышленности, которые обеспечивают выпуск конечной продукции. Расчет по частям позволяет снизить объемы вычислений, а возможность на сетевой модели оценить изменение состояния системы при изменении хозяйственных связей провести анализ проектируемых структурных реформ, ввод новых и закрытие старых предприятий, создание новых рынков сбыта, источников ресурсов.