Сетевая модель шахтной вентиляции добывающих предприятий

Производство энергии является ключевым фактором устойчивого развития страны.

Подземная добыча ресурсов требует вентиляции шахт, роль которой сохранится при переходе к технологиям без людей.

Президент Российской Федерации В.В. Путин 22.12.2020 на встрече с Заместителем

Председателя Правительства А.В. Новаком поздравил его и всех энергетиков страны с Днём энергетика, который совпал со 100-летием плана ГОЭЛРО. План был разработан государственной комиссией и принят в декабре 1920 года. Комиссию возглавлял Глеб Максимилианович Кржижановский, участвовало более 200 специалистов, а наша школа электротехники остается одной из лучших мире.

А.В. Новак отметил, что тогда было всего полгигаватта мощностей, 13 электростанций, и надо было их соединить. До этого они работали без соединения. В течение 15 лет предполагалось построить ещё 30 электростанций, 20 теплоэлектростанций и 10 гидроэлектростанций. План был перевыполнен, за шесть лет всё было построено, и общая мощность была увеличена на 1750 мегаватт.

На сегодня электроэнергетическая система России занимает первое место по охвату территорий и четвёртое место по выработке электроэнергии. Выработка электроэнергии составляет триллион сто, отметил А.В. Новак. У нас самая надёжная энергетическая система, несмотря на то, что мы занимаем четвёртое место по выработке, потому что требования, которые установлены, дают более высокую надёжность, защиту потребителей от технологических нарушений. Сегодня у нас 253 тысячи мегаватт. Это почти в 500 раз выше, чем на момент реализации плана ГОЭЛРО, 2,6 миллиона километров электрических сетей.

Энергосистема России является самой диверсифицированной в мире, экологичные источники энергии – атом, гидроэнергетика составляют суммарно 36%, есть 1000 мегаватт солнечной и ветряной электроэнергии. В энергобалансе 50% электростанций, работающих на газе, и всего 14% – на угле. В настоящее время общая энергосистема состоит из 1000 электростанций. Есть 12 атомных электростанций, около 170 гидроэлектростанций, 935 тепловых электростанций, построено более ста ветряных электростанций и солнечных электростанций. Был принят закон о микрогенерации. Это позволяет в жилых домах устанавливать солнечные батареи или ветрогенерацию, до 15 киловатт, и использовать для собственных нужд, а излишки продавать в сеть. Это позволяет экономить средства и иметь даже доход от продаж в энергосистему.

Таким образом, в энергобалансе России уголь не играет ведущей роли. Однако уголь играет большую роль в энергобалансе многих стран – Китая, Индии, США. Уголь имеет высокую долю в энергетическом балансе США, Японии, Германии, Южной Кореи. Добыча угля во всем мире имеет большие риски для людей. Кроме рисков шахтеров при добыче, есть риски использования угля. В Китае, например, это приводит к значительному загрязнению атмосферы, что вносит определенный вклад в глобальное потепление. При повышении температуры тает вечная мерзлота, освобождая углекислый газ в болотах Западной Сибири. Поступая в атмосферу, газ увеличивает потепление, что разгоняет извлечение газа. Потепление вызывает таяние ледников, повышение уровня Мирового океана, затопление жилых территорий. Это создает потенциал для перемещения людей, на фоне роста населения в Африке, ведет к борьбе за возвышенные территории. Поставки газа из России в Китай (удвоятся в 2021 году) снижают сжигание угля, уменьшают рост потепления.

Возрастание специализации, потоков в глобальных сетях увеличивает роль структуры при проектировании, управлении, обеспечении безопасности технических, экономических систем. Например, в карьерах, шахтах возникают или закрываются пути транспортировки продукции, меняются системы энергоснабжения, вентиляции, и т.д. Это требует расчета поведения систем с переменной структурой. Математической основой исследования поведения систем при изменении структуры является тензорный метод, в котором система, и процессы в ней, рассматриваются как тензор, а состояния процессов в разных структурах – как проекции в разные системы координат.

Г. Крон применил тензоры для создания общей теории электрических машин, которые рассматриваются как проекции обобщенной машины в разные системы координат, а затем тензорного анализа сетей [1]. Переход от одной машины или сети к другой описывают матрицы соединения, или матрицы изменения структуры. Тензорный метод, и его развитие, диакоптика, применялся для построения сетевых моделей различных предметных областей с использованием аналогий процессов и структуры [2, 3].

Особенность тензорного метода для исследования структуры сложных систем состоит в том, что при изменении структуры меняются границы элементов, замкнутые пути размыкаются, или замыкаются разомкнутые пути; матрицы преобразования становятся прямоугольными. В геометрии размерность пространства не меняется при изменении системы координат. В пространстве структуры координатами являются замкнутые и разомкнутые пути, которые составляют два ортогональных подпространства. Преобразования структуры связывает инвариант двойственности, состоящий в постоянстве суммы метрических тензоров двух двойственных сетей при изменении их структуры [4, 5].

Метод применяется для расчета сложных систем по частям [2-4, 12], что позволяет снизить объемы вычислений. Созданы сетевые модели для расчета межотраслевого баланса [4-6], систем квантовых состояний [5, 6, 9], тензорных моделей нейросетей [8, 11], теории инвариантов [10], в других областях, включая современные информационные системы.

В геометрии и физике размерность пространства не меняется при изменении системы координат. Особенность тензорного метода исследования сложных систем состоит в том, что при изменении структуры меняются границы элементов, замкнутые пути размыкаются, или замыкаются разомкнутые пути. В пространстве структуры координатами являются замкнутые и разомкнутые пути, которые составляют два ортогональных подпространства. Их размерности при изменении структуры меняются, матрицы преобразования путей становятся прямоугольными. Преобразования координат в структуре связывает инвариант двойственности, состоящий в постоянстве суммы метрических тензоров двух двойственных сетей при изменении их структуры. В физике данному инварианту соответствует закон сохранения потока энергии (постоянство суммы рассеиваемых мощностей двух двойственных электрических цепей при изменении соединения ветвей).

Преобразования компонент процессов в сетевой модели аналогичны преобразованию тензоров. Они обеспечивают переход от параметров процессов в одной структуре системы к другой структуре, как преобразование координат. Это обеспечивает расчет и анализ вариантов конструкции сложной системы при проектировании или анализировать Международный электронный журнал. Устойчивое развитие: наука и практика [Электронный ресурс] / гл. ред. А.Е. Петров. – Дубна : 2008-2020. – ISSN 2076-1163. – Режим доступа: возможные изменения процессов в системе при аварийных ситуациях, вызванных разрушением элементов, отключением подсистем, и т.д.

Тензорный метод позволяет создавать сетевые модели сложных систем разных предметных областей. Применение тензорного метода позволило получить алгоритмы расчета сетей при изменении структуры, например, при разделении сети на части или соединении из частей целого, что обеспечивает параллельные вычисления на суперкомпьютерах. Декомпозиция сетевой модели на подсети и расчет по частям ускоряет расчеты и позволяет решить проблему больших данных.

Сетевые модели используют аналоги между исследуемой системой и сетью для представления одновременно структуры и процессов. Например, сетевая модель системы производства представляет потоки продуктов двойственными узловыми и контурными токами, что обеспечивает снижение объема плановых расчетов. В ректификационной колонне двойственность позволяет представить узловой подсетью тепловой баланс, а контурной подсетью – материальный баланс по аналогии с параметрами теплообмена и массообмена. При изменениях структуры установки (аварии, повреждения) модель осуществляет расчет изменения потоков энергии, показывая опасные участки. Модель используется для обучения в Академии пожарной службы МЧС.

В данной статье рассматривается сетевая модель шахтной вентиляции для расчета и анализа воздушных (газовых) потоков при возможных обрушениях, отключениях различных ходов, вызванных аварийными ситуациями.

2.    Тензорный метод двойственных сетей

Структура системы меняется при проектировании, в процессе эксплуатации, при возникновении аварийных ситуаций. При проектировании системы необходимо рассматривать варианты конструкции при различных конфигурациях расположения и соединения элементов с целью создания оптимального варианта по параметрам эксплуатации, экономики и безопасности. При эксплуатации создаются новые штольни, штреки, стволы при включении в разработку новых горизонтов, пластов, рудных тел; при изменении транспортных путей в процессе разработки карьера, и т.д. При создании систем обеспечения безопасности необходим анализ поведения системы при разрушении, отключении отдельных элементов, подсистем, участков.

Тензорный метод основан на применении измеримых величин, и обеспечивает расчет и анализ поведения технических и экономических систем. Тензор характеризуют параметры процессов, которые представлены компонентами в системе координат. При переходе к другой системе координат компоненты тензора преобразуются по линейному закону.

Пространство структуры является дискретным, например, в электрической цепи рассматриваются только ветви – каналы распространения потока электрической энергии. Метод применяется для исследования поведения системы при изменении структуры. Это дает возможность получать описание состояния системы при разных структурах соединения элементов как преобразование описания состояния только одной структуры, для которой решение получено.

В качестве известного, полученного решения удобно выбрать систему, сетевую модель из отдельных, не соединенных элементов. Ее решение обычно достаточно просто, поскольку элементы не взаимодействуют. Затем решение для требуемой структуры получим с помощью матриц преобразования, которые показывают, как изменились пути при соединении отдельных элементов. Сетевая модель, которая объединяет описание процессов и структуры проектируемой системы, в данном случае для горной промышленности.

Соединение ветвей сети отображает структуру соединения элементов системы. Воздействия, отклики, метрика в ветвях сети отображает процессы, протекающие в системе в виде потоков одних величин под действием других величин при сопротивлении материи системы. Изменение соединений ветвей отображает изменение структуры системы.

Координатами в пространстве структуры являются замкнутые и разомкнутые пути, базисы которых определяют два ортогональных и взаимно дополняющих подпространства в пространстве сети. При изменении структуры меняется число замкнутых и разомкнутых путей, соответственно меняются размерности их подпространств.

Преобразование координат в структуре обеспечивает инвариант двойственности, который состоит в постоянстве суммы метрических тензоров двух двойственных сетей при изменении их структуры. В физике данному инварианту соответствует закон сохранения потока энергии.

Замкнутые пути описывают потоки от внутренних воздействий, отклики на которые не выходят за пределы системы. Разомкнутые пути описывают потоки от внешних воздействий, которые действуют извне на границы системы, отклики на них поступают в систему на одной границе, и покидают ее на других границах, выходя за пределы системы.

Метрические тензоры представляют собой матрицы решения сетей. Это означает, что при умножении метрической матрицы на вектор воздействия получается решение, т.е.

отклики в элементах системы, характеризующие состояние процесса.

Расчет контурной сети при внутренних воздействиях, производится по формуле i c = ^mC t (^mC Z ^mC t )^{-1 m}C e                                       (1)

Выражение перед вектором источников e обозначим Y c и назовем матрицей решения.

Это метрический тензор связанной контурной сети.

Y c = ^mC t (^mC Z ^mC t )^{-1 m}C

Расчет узловой сети при внешних воздействиях, производится с помощью матрицы решения Z c , которая представляет собой метрический тензор связанной узловой сети.

Z c = ^jA t (^jA Y ^jA^{`</sup> t )<sup>-1 j`}                                                      (3)

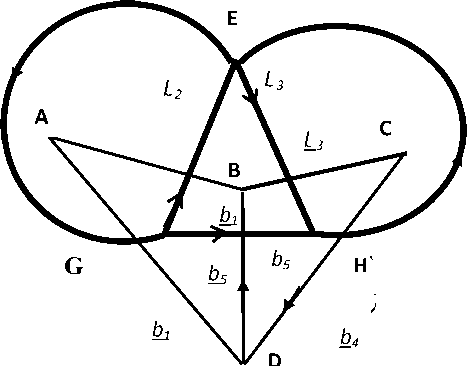
Двойственные сети дополняют друг друга до полного пространства структуры. Каждому замкнутому пути в данной сети соответствует разомкнутый путь в двойственной сети, и наоборот. Открытому пути в одной сети соответствует замкнутый путь в двойственности сети, и наоборот. При изменении структуры размыканию пути в одной сети соответствует замыкание пути в двойственной сети, и наоборот. Пример двойственных сетей и матриц преобразования путей представлен на рисунке 1, где жирные линии – ветви данной сети, тонкие линии – ветви двойственной сети.

Данная сеть

b 1

b ₃

b 2

b 3

Двойственная сеть b4

Рис. 1. Две двойственные сети из 5 ветвей

Структуру описывают матрицы преобразования путей старого базиса свободных ветвей в новый базис путей в связанных ветвях. Матрица преобразования данной сети C, а матрица преобразования двойственной сети С = А= С 1 .

	P 1	P2'	P s	P 4 '	P s			P1"	P2"	Ps"	P4"	Ps"
P1"	1	1				m	P 1	1					j
P2"		1	1		-1	m	P2'	-1	1	1			j
Ps"			1	1		m	Ps'	1	-1	1			j
С = P 4"				1		j	С = А = P 4'	-1	1	-1	1		m
Ps"					1	j	P s	-1	1			1	m

Матрицы преобразования имеют нулевой блок, поскольку нельзя выразить разомкнутые пути через замкнутые пути . Замкнутый путь создает новое измерение -охватывает часть двумерной поверхности. Матрица преобразования отображает выбор путей на ветвях сети. Базис замкнутых путей (контуров) должен охватывать все ветви, а базис разомкнутых путей должен охватывать все узлы (границы ветвей).

Пространство-структура существует только вдоль элементов сети (системы). Оно состоит из подпространств замкнутых и разомкнутых путей. Новым свойством является инвариант: постоянство суммы метрических тензоров двух двойственных сетей, что обеспечивает соединения и разъединения в сети. Векторы в пространстве сети представлены ковариантными и контравариантными проекциями в базисе замкнутых и открытых путей.

Замкнутые пути определяют базис путей для замкнутых систем, а разомкнутые пути определяют базис путей для открытых систем. Подпространства замкнутых и открытых путей взаимно дополняют друг друга до полного пространства, а их независимость (ортогональность) позволяют использовать эти свойства для сетевого моделирования сложных систем.

Инвариант двойственности представляет собой постоянство суммы метрических тензоров структуры контурных и узловых сетей, или двух двойственных сетей:

I = ^mC_t ( m C ^mC t )^{1 m}C + ^jA_t (A ^jA t )^{1 j}A (4) и их равенство единичной матрице, представляющей в данном случае метрический тензор свободных ветвей при единичной метрике.

При расчете электрических цепей и сетевых моделей сложных систем проводится проверка откликов на приложенные внутренние воздействия (источники напряжения) и внешние воздействия (источники тока) по законам Кирхгофа. Закон сохранения потока энергии выражается в постоянстве мощности mP0 в простейшей сети и в сумме двух двойственных сетей с данной структурой mPc и с двойственной mPc структурой mP0 = mPc + mPc.                                         (5)

3.    Сетевая модель системы вентиляции шахты

Цель создания сетевой модели состоит в анализе и проектировании поведения сложных систем с переменной структурой в горной промышленности. Модель шахты включает в себя воздействия: потоки массы породы и полезного ископаемого на выход, поток крепежа, поток энергии, поток воды на вход, а также потоки воздуха в системе вентиляции шахты. Рассмотрим построение сетевой модели для анализа процессов в системе вентиляции шахты.

Система, вентиляции шахты, электроснабжения, пути транспортировки продукции могут быть представлены сетевой моделью. На рисунке 2 представлен пример подземных коммуникаций для фрагмента системы вентиляции и справа два варианта сетевой модели. На верхнем варианте сетевой модели разделены входной и выходные потоки воздуха. Подматрица замкнутых путей содержит две строки, а висячие ветви не содержат потоков, поскольку в метрической матрице соответствующие им строки и столбцы нулевые. При расчете сетевой модели как контурной сети или узловой сети, получаемые отклики не соответствует исследуемой системе. Более адекватной системе вентиляции является нижний вариант сетевой модели, в котором узлы входа и выхода соединены подобно заземлению в электрической цепи. Это отражает баланс – потоки воздуха на входе должны равняться потокам на выходе из шахты. Рассматриваем модель как контурную сеть, в которой источники воздействия – нагнетающие и откачивающие насосы представлены по аналогии источниками напряжения (ЭДС), а потоки воздуха моделируют электрические токи. Величины в сети подчиняются законам Кирхгофа. Входящие потоки воздуха (токи) в каждом узле и выходящие потоки равны друг другу, а сумма перепадов давлений (падений напряжения), по каждому контуру равна нулю.

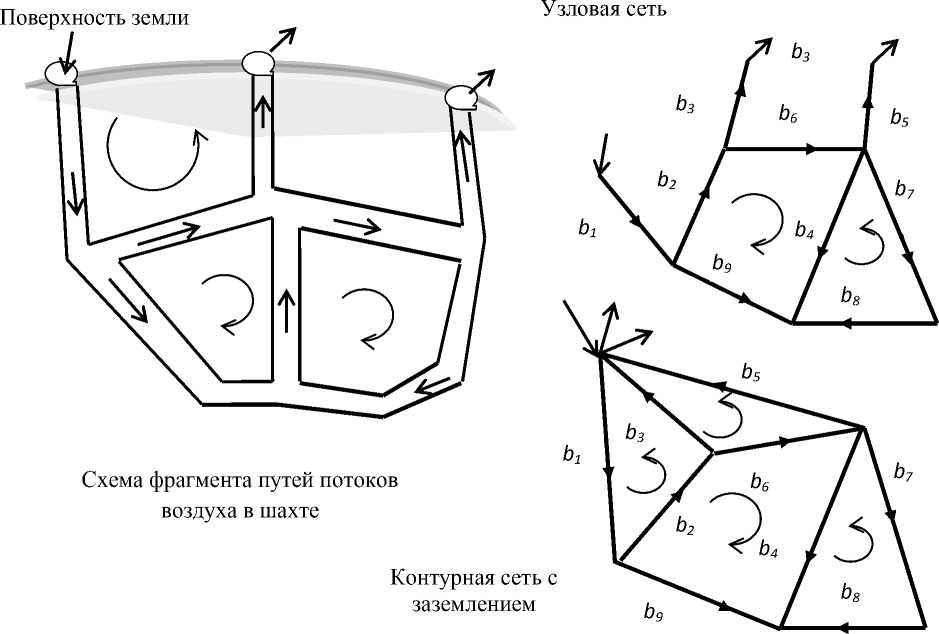
Рис. 2. Фрагмент системы вентиляции шахты и варианты сетевой модели

Матрица преобразования путей сетевой модели, представленной справа на нижней схеме, где показаны замкнутые пути, а разомкнутые проходят по соответствующим ветвям, имеет следующий вид:

	1	2	3	4	5	6	7	8	9
1	1	1	1	0	0	0	0	0	0
2	0	1	0	1	0	1	0	0	-1
3	0	0	1	0	-1	-1	0	0	0
4	0	0	0	1	0	0	-1	-1	0
5	0	0	0	0	1	0	0	0	0
6	0	0	0	0	0	1	0	0	0
7	0	0	0	0	0	0	1	0	0
8	0	0	0	0	0	0	0	1	0
9	0	0	0	0	0	0	0	0	1

Первые четыре строки представляют собой подматрицу контуров, замкнутых путей. Преобразование путей в узловой сети определяет подматрица открытых путей ортогональной матрицы преобразования путей.

Для простоты допустим, что метрические характеристики ветвей (сопротивления электрической цепи), равны единицам. Тогда матрица решения (метрический тензор связанной сети) получаемая для контурной сети по формуле (1), будет равна:

	1	2	3	4	5	6	7	8	9
1	30	18	16	-8	14	2	-4	-4	12
2	18	30	16	8	2	14	4	4	-12
3	16	16	32	0	-16	-16	0	0	0
4	-8	8	0	32	-8	8	-16	-16	-16
5	14	2	-16	-8	30	18	-4	-4	12       1/64
6	2	14	-16	8	18	30	4	4	-12
7	-4	4	0	-16	-4	4	24	24	-8
8	-4	4	0	-16	-4	4	24	24	-8
9	12	-12	0	-16	12	-12	-8	-8	24

Все элементы для наглядности даны целыми числами; их надо разделить на значение определителя, который равен 64 и показан справа от матрицы. Допустим, что воздействия в сети вентиляции заданы насосами, расположенными в ветвях 1, 3, 5, имея значения, представленные вектором ei

1         2         3         4         5         6         7         8         9

100

0

40

0

60

0

0

0

0

Умножая матрицу решения на вектор воздействия, получим отклики – токи на ветвях, которые моделируют потоки воздуха в шахте:

1         2         3         4         5         6         7         8         9

70

40

30

-20

40

10

-10

-10

30

¹i k =

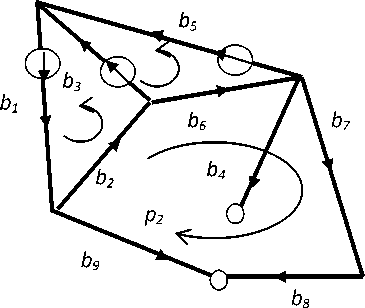
Эти значения показаны на рисунке 3 справа, где слева показана схема участка шахты, в которой изменилась структура (вариант проектирования или аварийная ситуация).

Поверхность земли

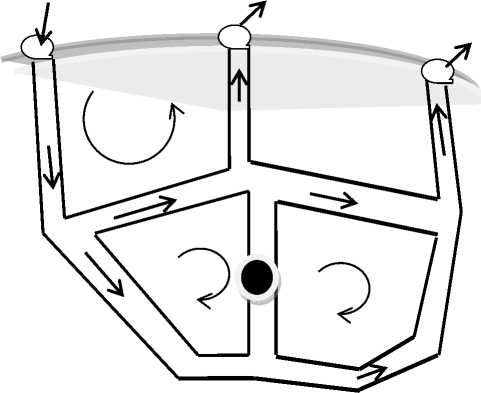
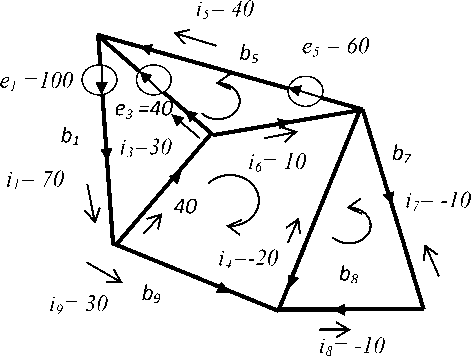
Схема потоков воздуха в шахте с аварийным участком

Источники воздействия и потоки в ветвях

Рис. 3. Результаты расчета сетевой модели

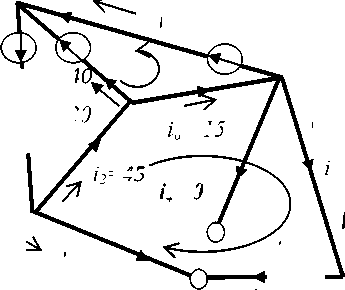
Полученные значения удовлетворяют законам Кирхгофа. Допустим, что произошли изменения в структуре, например, завален или разрушен ход, которому в модели соответствует ветвь 4. Структура сетевой модели меняется, как показано на рисунке 4. Теперь замкнутый путь 4 становится разомкнутым, а путь 2 проходит по другим ветвям.

i 5 = 35

b 7

_b5     e 5 = 60

e 1 =100

e 3 =4

b 1

i 3 =30

i 1 = 65

i 6 = 15

= 45

i 4 = 0

i 7 = -20

b 8

i 8 = -20

i 9 = 20 ^b9

Сетевая модель потоков воздуха в шахте с аварийным участком

Источники воздействия и потоки в ветвях сети с аварийным участком

Рис. 4. Структура и результаты расчета сетевой модели с аварийным участком

Это показано в контурной матрице преобразования, которая теперь состоит из трех строк, представляющих контуры, замкнутые пути.

	1	1	2	3	4	5	6	7	8	9
		1	1	1	0	0	0	0	0	0
mC =	2	0	1	0	0	0	1	1	1	-1
	3	0	0	1	0	-1	-1	0	0	0

Проводя вычисления при тех же источникам воздействия, получим отклики, новые потоки в ветвях (ходах шахты).

	1	2	3	4	5	6	7	8	9
2i k =	65	45	30	0	35	15	-20	-20	20

Эти значения показаны на рисунке на схеме справа. Ниже представлены изменения значений потоков, процессов вентиляции в шахте, которые произошли при изменении структуры.

	1	2	3	4	5	6	7	8	9
1i k - 2i k =	5	-5	0	-20	5	-5	10	10	10

Такие отклонения в значениях потоков должны учитываться при проектировании различных вариантов системы, в данном случае, системы вентиляции шахты, при создании систем обеспечения безопасности с целью учета изменений при всех потенциально возможных видах возникновения аварийных ситуаций.

4.    Обсуждение результатов

Применение тензорного метода обеспечивает проектирование, анализ, управление систем при изменении структуры за счет применения матриц преобразования, двойственности, инвариантов, аналогий между системами и сетями. Расчеты показали, что для системы вентиляции шахты наиболее адекватна контурная сетевая модель, как и для модели массовых потоков системы ректификации. При нарушении структуры значения потоков меняются, указывая на уязвимые позиции для проектирования и управления.

Подобным образом можно проводить расчеты и анализ для сети энергоснабжения, водоснабжения, сети путей транспортировки материальных (продуктовых) потоков, обеспечивая единый метод анализа всей системы проектирования и управления шахтой.

Сетевая модель обеспечивает возможность создать базу данных примеров потенциально возможных аварийных ситуаций, и на модели определить порядок действий по выходу на нормативный режим функционирования, или комплекс мер по ликвидации последствий аварии и обеспечению безопасности персонала. Для применения тензорного метода с целью комплексного анализа всех видов материальных, энергетических, информационных потоков в системе горной промышленности, необходимо использовать ортогональность замкнутых и открытых путей, инвариант двойственности, закон сохранения потока энергии.

Заключение

Таким образом, тензорный метод обеспечивает построение сетевых моделей, которые позволяют объективно представить процессы и структуру систем горной промышленности, что обеспечивает возможности проектирования наилучших вариантов, оценить на модели потенциально возможные аварийные ситуации.

Тензорный метод обеспечивает исследования систем с переменной структурой, позволяет изучать изменения процессов при изменении структуры. Это актуально в условиях роста специализации и постоянного изменения технологий.