Сетевая модель системы логистики

Потоки продуктов по путям перевозки имеют аналогии с потоками токов в электрической цепи. Роль логистики в процессах производства возрастает в связи со специализацией и разделением труда. До 90% времени производства продуктов высоких технологий составляет транспортировка компонент между пунктами различных производств.

Изменение и развитие технологий изменяет маршруты перевозок. Это требует расчетов изменения потоков продуктов в сетях перевозок при изменении потоков и структуры.

Например, как изменятся потоки при изменении структуры. Как изменится стоимость транспортировки потоков продуктов при изменении маршрутов перевозки.

Заданы спрос на продукты, объемы производства продуктов, схема маршрутов, путей транспортировки потоков. Каждому пути дана цена перевозки, тариф перевозки килограмма продукции по данному пути.

Произведение каждого тарифа на поток дает стоимость перевозки по данному пути, а сумма по всем путям – общую стоимость перевозки. Изменяя распределение потоков по путям с наиболее выгодной стоимостью можно снизить издержки, затраты на перевозку, транспортировку грузов.

Маршруты путей перевозки продуктов являются ветвями сети. Изменение маршрутов перевозок рассматривается как изменение границ соединения ветвей. Изменяются потоки по сети, при увеличении спроса и предложения поставок. Возникают новые маршруты или закрываются старые маршруты, необходимо изменить потоки продуктов. Изменить объемы, потоки перевозок по новым маршрутам.

В сетевой модели изменение маршрутов описывает матрица преобразования путей. Обратную логистику обеспечивает сеть движения потоков денежных средств, платежей за поставку продукции.

Меняется стоимость перевозки по разным путям – надо решить задачу минимизации стоимости.

Структура и процессы

Роль структуры возрастает. Мир состоит из структуры. В структуре движутся потоки энергии. Система состоит из элементов, соединенных своими границами. Каждый элемент определяет измерение в пространстве системы. Это пространство существует только в элементах, т.е. является дискретным относительно пространства геометрии, где есть непрерывность, всюду плотность, однородность, изотропность.

Элементами системы являются, например, маршруты перемещения грузов между различными пунктами (узлами). Это перемещения в пространстве. Если грузы остаются в одном пункте, то это хранение, перемещение во времени.

Координаты в структуре

В сетях координатами являются пути, которые определяют арифметизацию пространства в структуре. Путь – это линия, проходящая вдоль ветви, как ось координат вдоль измерения. Пути бывают либо замкнутые, либо разомкнутые.

Два типа путей, замкнутые и разомкнутые, образуют два независимых, ортогональных подпространства в структуре. При изменениях в структуре замкнутые и разомкнутые пути переходят друг в друга, поэтому меняются размерности их подпространств. Таким образом, в пространстве структуры базисы замкнутых и разомкнутых путей содержат не одинаковое количество элементов. Пути являются координатами пространства структуры при построении сетевых моделей систем.

Пути перемещения могут меняться, тогда меняется структура системы. Переход от одной структуры к другой обеспечивают матрицы преобразования путей. В элементах системы возникают процессы как потоки откликов на приложенные воздействия. Воздействия и отклики связаны через метрику, меру их взаимодействия, уравнениями поведения, которые не содержат описания структуры. Таким образом, описание структуры не содержит метрики, описание процессов, метрики, не содержит структуру.

Процессы и структура обладают свойствами двойственности, что позволяет, обеспечивает возможности расчета процессов пи изменении структуры.

Инвариант двойственных сетей

Изменение структуры сетей связывает инвариант двойственности. Он состоит в том, что постоянна сумма метрических тензоров двух двойственных сетей при изменении структуры связей, соединения ветвей.

Сети состоят из ветвей, одномерных отрезков, которые могут соединяться своими границами – узлами. Координатами в пространстве сети являются пути – линии, проходящие по ветвям, от одной границы к другой границе. Путь, который проходит по ветвям, и возвращается в начало – замкнутый, иначе – разомкнутый.

Сетевые модели позволяют представить процессы и структуру сложных систем, включая системы логистики. Инвариант двойственности показывает, что уменьшение потоков в одной сети вызывает увеличение потоков в другой сети с двойственной структурой.

Двойственность состоит в том, что замкнутому пути в одной сети соответствует разомкнутый путь в двойственной сети, и наоборот. Пути определяют координаты пространства сети, которое состоит из двух ортогональных подпространств замкнутых и разомкнутых путей. При изменении структуры происходит замыкание и размыкание путей, соответственно, меняется размерность их подпространств. Изменение размерности является особенностью преобразования структуры.

Структура сетей определяет свойства системы как открытой и замкнутой. Логистическая система является открытой и замкнутой. Свойства замкнутой системы определяет базис замкнутых путей. Свойства открытой системы определяет базис разомкнутых путей.

Инвариант двойственности и тензорная методология в теории систем

Система состоит из элементов, соединенных своими границами. Каждый элемент определяет измерение в пространстве системы. Это пространство существует только в элементах, т.е. является дискретным относительно пространства геометрии, где есть непрерывность, всюду плотность, однородность, изотропность.

Объекты в пространстве существуют независимо от наблюдателя. Для представления и анализа вводят системы координат, позволяющие представить объекты в цифровом виде как значения компонент вдоль систем координат.

В пространстве структуры системы координатами являются пути.

Элементы системы рассматриваются как объект, расположенный в пространстве. Пространство структуры состоит из двух пространств: замкнутых путей и разомкнутых путей. Эти особенности важны для структуры, однако они присущи и обычному пространству.

Поступательные движения в пространстве происходят по разомкнутым путям, вращательные движения происходят по замкнутым путям. Любое движение можно представить комбинацией поступательного и вращательного движения. Таким образом, замкнутость и открытость являются фундаментальными свойствами в геометрии и физике. Однако для структуры систем важным является переходы между разомкнутыми и замкнутыми путями, преобразование путей, поскольку при этом изменяется размерность подпространства, свойства структуры, и протекающих в ней процессов.

Инвариант двойственности является свойством пространства структуры, также как однородность, изотропность. Система из элементов, сеть имеет свойство двойственности. В системе возникают процессы как отклики на приложенные воздействия. Потоки процессов возникают в подпространстве замкнутых путей, или разомкнутых путей. Эти процессы не зависят друг от друга, поскольку подпространства ортогональны.

Система, состоящая из элементов, есть объект, а разные способы соединения элементов есть проекции этого объекта в разные системы координат. Когда характеристики объекта (проекции) при изменении системы координат меняются по линейным законам, то этот объект является тензором. Он существует сам по себе, а разные способы соединения элементов, или разный выбор путей являются его проекциями в системы координат.

Обобщенная система из элементов и процессов есть тензор, а сетевые модели разных предметных областей, включая системы логистики, являются ее проекциями в системы координат.

Сетевая модель Крона для транспортной задачи

Г. Крон создал сетевую модель для транспортной задачи [1]. Модель предназначена для решения по частям задачи линейного программирования (ЗЛП), и оптимизации стоимости перевозок. Продукты производителей надо доставить потребителям. Имеется много маршрутов доставки, которые отличаются длиной, скоростью, пропускной способностью и стоимостью перевозки единицы товара (тарифом). Задача состоит в том, чтобы выбрать маршруты с минимальной стоимостью доставки.

Для создания модели необходимо установить аналогии между понятиями моделируемой системы и сетью. Наиболее наглядной реализацией абстрактной сети является электрическая цепь. Достаточно очевидно, что потокам продуктов соответствуют токи. Предложение и спрос можно представить напряжениями, а тарифы – сопротивлениями (импедансами).

В сети есть шесть видов величин: импедансы и проводимости, контурные источники напряжения и токи отклика, узловые источники тока и отклики – напряжения. В транспортной системе есть три вида величин:  количество товаров, стоимость транспортировки и стоимость хранения. Хотя Крон считает, что транспортным ценам следовало бы поставить в соответствие импедансы или проводимости, однако затем он полагает, что этим величинам соответствуют единичные значения. В этом случае, заметим, ток и напряжение в каждой ветви численно равны. Далее стоимости транспортировки и хранения потоков продуктов на входе и на выходе рассматриваются как источники напряжений.

Такая сетевая модель не только реализует симплексный метод ЗЛП, но и позволяет решить задачу по частям. Такой подход позволил Крону представить целевую функцию как минимизацию мощности, однако при этом напряжение относится к контурной сети, а ток – к узловой сети. Потоки входа и выхода рассматриваются как источники тока. Потоки продуктов соответствуют сумме узловых и контурных токов, которые в каждой ветви остаются постоянными. Изменения соединения ветвей (выбор маршрутов) меняют число замкнутых и разомкнутых путей, при этом меняются узловые и контурные составляющие тока. Надо достичь выбора маршрутов, при котором мощность становится минимальной.

Симплексный метод проще и эффективнее, но, как считает Г.Крон, сетевая модель дает физическую интерпретацию, и позволяет применять декомпозицию для расчета по частям.

В настоящее время существуют различные методы решения транспортной задачи: метод северо-западного угла, метод потенциалов, варианты симплексного метода.

Классическая постановка транспортной задачи имеет вид [4]:

Минимизировать целевую функцию XXc ij x ij => min ,                           (1)

где i = 1, m; j = 1, n. Здесь обозначены стоимость транспортировки единицы продукта c ij и объем перевозимого продукта x ij .

При этом система ограничений поставок S i и спроса D j имеет вид:

Поставки (наличные ресурсы): 2 xij = Si(2)

Спрос потребителей: 2 xij = Dj(3)

Переменные принимают неотрицательные значения, т.е.

xij > 0 для всех значений i и j.(4)

Все S i и D j – неотрицательные целые числа, удовлетворяющие условию

2 S i = 2 D j , (т.е. имеется баланс – сумма поставок равна сумме спроса).

Многие оптимизационные задачи на сетях можно преобразовать в эквивалентную классическую транспортную задачу. В данной задаче основными элементами являются транспортные маршруты, также могут рассматриваться склады. Продукты перевозят (осуществляют транспортировку в пространстве) или хранят на складах (осуществляют транспортировку во времени). Стоимость перевозки c ij в одном направлении и хранения на складах единицы товара для каждого маршрута задает объединенная матрица.

Для минимизации целевой функции надо найти, выбрать такие маршруты, которые позволят выполнить необходимые перевозки для заданного интервала времени с наименьшими затратами.

Методология

Для моделирования применяется тензорный метод двойственных сетей, который обеспечивает представление процессов и структуры в системе. Структура связи элементов в системе, в данном случае, путей доставки продуктов, меняется в силу разных причин.

Для создания сетевой модели предметной области тензорным методом необходимо рассмотреть простейший вариант системы, обладающий всеми отличительными свойствами. Полученное соответствие между системой и сетью можно переносить на более сложные варианты системы с помощью матриц преобразования структуры.

Основой является применение тензорного метода расчета сетей с внутренними и внешними источниками воздействия, где используются матрица преобразования структуры.

Пусть имеются свободные ветви-контуры, с уравнением (5) e a = Z ab i^b . Соединим ветви в новую, связанную сеть, уравнение поведения которой:

e a` = Z a`b` i<sup>b`</sup>                                                                                              (6)

Матрица ^mC выражает базисные пути в связанной сети через пути в свободных ветвях.

Подставим в (6) формулы (3.4), (3.7) и (3.9) из [3]:

том 17 № 3 (52), 2021, ст. 1

m a`

e a

ma mb

t ` i

b`

и, решая это матричное уравнение, получим токи в базисных контурах связанной сети через воздействия в свободных ветвях:

i^b` = (<sup>m</sup>C a` ^a Z ab ^mC b` <sup>b</sup> t )<sup>-1 m</sup>C a` ^a e a

Перейдем от откликов (токов) в путях-контурах к измеримым величинам в отдельных ветвях связанной цепи, которые обозначим i bс b    m a b    m a m a    m b -1 m a

Выражение перед вектором источников e a обозначено как Y c и названо « матрица решения» . Y c = ^mC a` <sup>a</sup> t (<sup>m</sup>C a` ^a Z ab ^mC b` <sup>b</sup> t )<sup>-1 m</sup>C a` ^a

Это «обобщенный» метрический тензор связанной контурной сети.

Напряжение в каждой ветви связанной сети получим, умножая ее импеданс на ток в ветви: e a ^с = Z ab i^b с .

Матрица решения сети для внутренних источников воздействия (например, источников напряжения, ЭДС в электрической цепи):

Y c = ^mC t ( ^mC Z ^mC t )^{-1 m}C                                                                (9)

Базисом являются независимые замкнутые пути.

Матрица решения для внешних источников воздействия (например, источников тока в цепи) получается заменой всех величин на двойственные: Z на Y, ^mC на ^jА

Z c = ^jА t (^jА Y ^jА t ) ^{-1 j}А                                                                        (10)

Базисом являются независимые разомкнутые пути.

Умножение матрицы решения на вектор воздействий дает отклики (например, контурные и узловые токи) в связанной сети.

Матрица решения есть метрический тензор связанной сети, выраженный через метрический тензор (матрицу импедансов) простейшей сети Z = Y^-1 из свободных ветвей и матрицу преобразования структуры ^mC .

Модель системы перевозок

Предложения представляют источники напряжения в ветвях входа (склады поставок продуктов). Спрос представляют источники напряжения в ветвях выхода (склады потребителей продуктов). Маршруты представляют ветви, соединяющие выход поставщика и вход потребителя. Все входы ветвей поставщиков заземлены. Все выходы ветвей потребителей также заземлены.

Если рассматривать в качестве воздействий источники тока, то получатся лишние потоки, которые не соответствуют физической сути процесса перевозки продуктов. Дело в том, что источник тока в несоединенных ветвях сети из свободных, ветвей входит в один узел ветви, а выходит из другого узла. Когда ветви соединены, ток источника также входит в один узел, а выходит из другого узла «своей» ветви.

В логистической сети потоки продуктов покидают выход поставщика и поступают в маршруты, пути, по которым они идут к потребителям. Нет никакого выхода за пределы данной сети, данной системы. Такая же проблема возникала при разработке сетевой модели межотраслевого баланса [2, 3, 7]. Проблема решена там за счет использования потоков в двойственной контурной сети.

Сеть с источниками напряжения в ветвях поставщиков и потребителей

Источники напряжения в ветвях поставщиков представляют потоки предложения. Источники напряжения в ветвях потребителей представляют потоки спроса. Потребителей и поставщиков связывают ветви, представляющие маршруты. Решение задачи сети для данной модели дает некоторое, но неполное, распределение потоков продуктов по маршрутам от поставщиков к потребителям. Для получения распределения полных потоков в сети необходимы дополнительные источники.

Разность между заданными и полученными откликами в ветвях входа и выхода указывает, что существуют дополнительные источники, которые приводят сумму токов в ветвях сетевой модели к значениям, соответствующим потокам продуктов в логистической системе. Эти дополнительные источники должны располагаться в ветвях, соответствующих маршрутам, которые определяют базис замкнутых путей в данной сети.

Расчет дополнительных потоков в маршрутах обеспечивает баланс токов по закону Кирхгофа в узлах соединения ветвей маршрутов с ветвями входа и выхода. Особенность сетевой модели данной предметной области состоит в том что, между балансами тока в этих узлах существует линейная зависимость. По этой причине необходимо задать (выбрать или назначить) дополнительный ток в одной из ветвей маршрутов, что позволяет получить остальные токи, численно равные дополнительным потокам продуктов в логистической системе. Полученные в результате токи, в сумме с токами, полученными при первом расчете, соответствуют одному из вариантов решения задачи транспортировки продуктов от производителей к потребителям. Процедура назначения одного из дополнительных токов может рассматриваться как выбор приоритетного направления с заданным потоком, который должен быть сюда доставлен.

том 17 № 3 (52), 2021, ст. 1

Согласно тензорной методологии, сначала рассмотрим наиболее простую транспортную систему и потоки в ней. Пусть в этой системе один поставщик, два потребителя, два маршрута и она представлена на рисунке 1 слева. Поток продукта от производителя в 100 единиц поставляется по двум маршрутам к двум потребителям, получающим 70 и 30 единиц продукта соответственно. Здесь потоки по маршрутам равны потребностям потребителей, так что их распределение однозначно.

Этой системе соответствует сеть из пяти ветвей, представленная на рисунке 1 справа. Можно видеть, что структура сетевой модели отличается структуры логистической системы. Поскольку имеется равенство поставки и потребления, то вход производства и выход потребления можно рассматривать как «заземление» и связать их в одном узле D .

В результате в сетевой модели возникают два замкнутых пути, контура, которых в транспортной системе быть не должно. Вместе с тем оказалось, что именно такая структура сети позволяет адекватно представить потоки продуктов в транспортной системе. В сетевой модели воздействия представлены источниками напряжения с аналогичными значениями, которые расположены в ветвях входа и выхода.

Поставка продукта

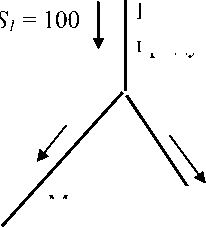
Маршруты перевозок d2 =70

Потребители

d 3 =30

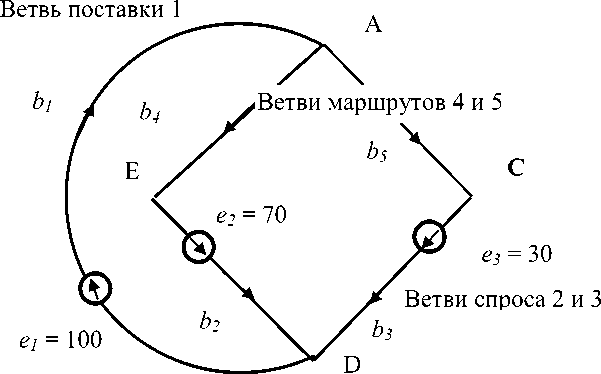
Система перевозки: поставщик, два маршрута и два потребителя

Сетевая модель системы перевозки из 5 ветвей

Рис. 1. Простая транспортная система и ее сетевая модель из 5 ветвей

Рассмотрим сетевую модель как контурную сеть, в которой есть баланс потоков продуктов на входе и на выходе, что выражается «заземлением» этих потоков в узле D . Матрица преобразования от сети из отдельных ветвей к связанной сети, в которой строки указывают выбор путей, имеет вид:

www.rypravlenie.ru					том 17 № 3 (52), 2021, ст. 1
	1	2	3	4	5
1	1,0	0,0	0,0	0,0	0,0
2	0,0	1,0	0,0	0,0	0,0	jC
С =        3	0,0	0,0	1,0	0,0	0,0
4	1,0	1,0	0,0	1,0	0,0	mC
5	1,0	0,0	1,0	0,0	1,0

Ветви входа и выхода определяют разомкнутые пути. Это первые три строки, которые составляют матрицу ^jC. Ветви маршрутов определяют замкнутые пути. Это последние две строки, они составляют матрицу ^mC , которая обеспечивает расчет контурной сети с помощью матрицы решения Y c .

Получим выражение в скобках ^mC ^mC t = z` =

1      2      3      4      5

1	1	0	1	0
1	0	1	0	1

*

	4	5
1	1	1
2	1	0
3	0	1
4	1	0
5	0	1

4		5
4	3,00	1,00
5	1,00	3,00

Обращая полученную матрицу z`, и умножая ее слева на mCt, а справа на mC, получим матрицу решения Yc = mCt (z`)-1 mC =

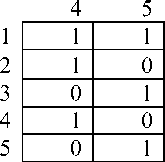
4      5

0,38	-0,13
-0,13	0,38

1      2      3      4      5

* 4

1	1	0	1	0
1	0	1	0	1

= Y c

Чтобы не переписывать, умножим сразу эту матрицу решения на вектор воздействия, заданный предложением и спросом, и представленный источниками напряжения e, тогда получим отклики, токи в ветвях контурной сети mic. В силу единичных сопротивлений, эти токи численно равны напряжениям на ветвях mic = mec.

1 2	1	2	3	4	5	1 2	e	1 2	mi c = me c
	0,50	0,25	0,25	0,25	0,25		100		75,0
	0,25	0,38	-0,13	0,38	-0,13		70		47,5
Y c = 3	0,25	-0,13	0,38	-0,13	0,38	*          3	30	=       3	27,5
4	0,25	0,38	-0,13	0,38	-0,13	4	0	4	47,5
5	0,25	-0,13	0,38	-0,13	0,38	5	0	5	27,5

Это токи, которые должны быть аналогами потоков продуктов в логистической сети. Но полученные токи не соответствуют потокам продуктов, которые надо транспортировать от входа к выходу. Однако можно дополнить эти токи с помощью источников воздействий в ветвях маршрутов, в какой-то степени используя двойственную сеть.

том 17 № 3 (52), 2021, ст. 1

Рассмотрим разности между заданными токами в простейшей сети и полученными в результате расчета. Эти разности можно рассматривать как отклики в сети, которые дополнят токи на входе и на выходе так, чтобы суммарные токи в ветвях маршрутов соответствовали транспортировке продуктов от производителей к потребителям.

1	100	1	75,0	1	25,0
2	70	2	47,5	2	22,5
3	30	-        3	27,5	=         3	2,5
4	0	4	47,5	4	-47,5
5	0	5	27,5	5	-27,5

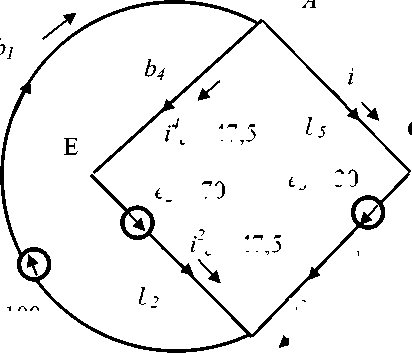
Полученные разности также соответствуют токам в двойственной сети в силу инварианта двойственности. Результаты расчета контурной сетевой модели (токи, численно равные напряжениям в силу единичных сопротивлений), показаны на рисунке 2 слева.

Дополнительные токи в сетевой модели, которые соответствуют токам в двойственной сети, показаны на рисунке 2 справа. Они обозначены индексом d , например, i¹ c d = 25. Задача состоит в том, чтобы найти новые, дополнительные источники, которые дополнят токи в ветвях на входе и на выходе до потоков поставки и спроса. Тогда в ветвях маршрутов суммарные токи дадут потоки перевозки продуктов от производителей к потребителям. В данном случае неизвестными являются дополнительные токи в маршрутах, в ветвях 4 и 5. Эти ветви, в силу выбора путей, определяют базис контуров в структуре сети, а токи в них равны контурным токам.

Это значит, что источники напряжения в этих ветвях могут дать нам необходимое дополнительное распределение токов по ветвям, которое в сумме с уже полученными, будет соответствовать решению задачи транспортировки продуктов. Неизвестные дополнительные токи в маршрутах, в данном случае, в ветвях 4 и 5, можно получить из условия баланса токов в узлах сети E и C по закону Кирхгофа .

том 17 № 3 (52), 2021, ст. 1

e 1 = 100

i⁵ c = 27,5

i¹ c = 75

b 5

i c =47,5

e 3 = 30

e 2 = 70

i c =47,5

b 2

C b3

i³ c = 27,5

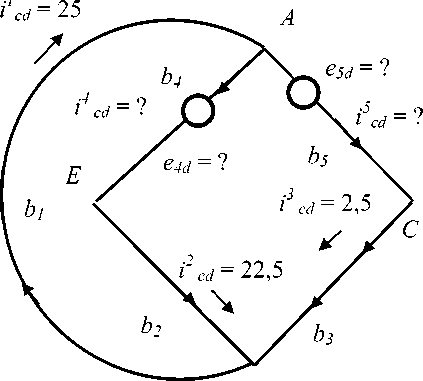
Токи на ветвях контурной сетевой модели

Дополнительные токи на ветвях сетевой модели, их надо рассчитать

Рис. 2. Результаты расчета контурной сети и данные для дополнительных токов

Таким образом, рассмотрим баланс токов в узлах, который в данном случае является весьма простым. Из узла E выходит ток, равный i² cd = 22,5, следовательно, ток в маршруте 4 равен i⁴ cd = 22,5. Аналогично, из анализа узла получим, что ток в ветви 5 равен i⁵ cd = 2,5. Сумма этих токов равна току в ветви 1, i¹ cd = 25, что является проверкой баланса в узле A .

Полученные токи являются контурными токами i` d в прежней сети с новыми источниками. По ним можно получить дополнительные токи во всех ветвях по обычной формуле:

^mi cd = ^mС t ^mi` d =

4        5

1	1	1
2	1	0
3	0	1
4	1	0
5	0	1

i` d

*  4	22,5
5	2,5

1	25,0
2	22,5
3	2,5
4	22,5
5	2,5

Также проведем расчет источников напряжения в ветвях маршрутов, которые обеспечивают дополнительные токи. Для этого умножим матрицу сопротивлений контуров связанной сети z` на вектор дополнительных контурных токов i`d.

4          5

е` d = z` i` d = 4	3,00	1,00
5	1,00	3,00

*  4	22,5
5	2,5

= 4

том 17 № 3 (52), 2021, ст. 1

Теперь, суммируя контурные токи в ветвях с дополнительными токами, получим распределение токов, соответствующее распределению перевозимых продуктов xij.

^mi c + ^mi cd = x ij

1	75,0
2	47,5
3	27,5
4	47,5
5	27,5

1	25,0	1	100,0
2	22,5	2	70,0
3	2,5	=          3	30,0
4	22,5	4	70,0
5	2,5	5	30,0

Получено правильное распределение потоков в сети, впрочем, достаточно очевидное для данного простого случая. Полученную методику моделирования применим для более сложного примера системы транспортировки продуктов.

Пример сетевой модели для системы транспортировки продуктов

На рисунке 3 представлена сетевая модель для системы транспортировки продуктов. Сама система логистики имеет вид такой же, как на рисунке 1, и здесь не показана, чтобы не усложнять рисунок. Сеть включает в себя двух поставщиков, представленных ветвями 1 и 2, трех потребителей – ветви 3, 4, 5, которые связаны пятью маршрутами – ветви 6––10.

Поток продукта от производителя в ветви 1 составляет 300 единиц, а производителя 2 – 200 единиц; требования потребителя в ветви 3 составляет 100, 4 – 350, и 5 – 50 единиц. Они представлены источниками напряжения в соответствующих ветвях на схеме. Пять маршрутов пока не имеют источников воздействия. Ветви входа и выхода определяют разомкнутые базисные пути, ветви маршрутов – замкнутые базисные пути.

Ветвь поставки

A

В e1 = 300

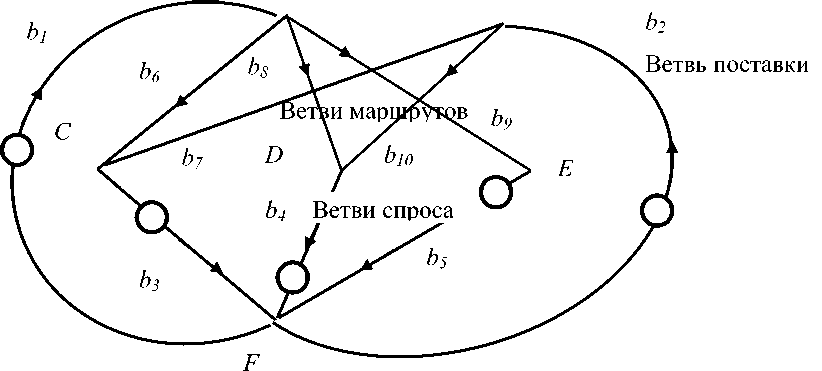
Рис. 3. Сетевая модель транспортной системы из 10 ветвей для двух поставщиков и трех потребителей

том 17 № 3 (52), 2021, ст. 1

Матрица преобразования путей описывает структуру системы перевозок продуктов. Матрица преобразования от сети из отдельных ветвей к связанной сети, в которой строки указывают выбор путей, имеет вид:

С =

1       2       3       4       5       6       7       8       9      10

1	1	0	0	0	0	0	0	0	0	0
2	0	1	0	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	0	0
4	0	0	0	1	0	0	0	0	0	0	jC
5	0	0	0	0	1	0	0	0	0	0
6	1	0	1	0	0	1	0	0	0	0
7	0	1	1	0	0	0	1	0	0	0
8	1	0	0	1	0	0	0	1	0	0	mC
9	1	0	0	0	1	0	0	0	1	0
10	0	1	0	1	0	0	0	0	0	1

Ветви входа и выхода определяют разомкнутые пути. Это первые шесть строк, которые составляют матрицу ^jC. Ветви маршрутов определяют замкнутые пути. Это последние шесть строк, они составляют матрицу ^mC , которая обеспечивает расчет контурной сети с помощью матрицы решения Y c .

Для расчета сетевой модели получим матрицу решения. Для простоты полагаем, что метрика, сопротивления ветвей, равны единицам. Далее сопротивления будут использованы для расчета финансовой составляющей потоков продуктов. При этих условиях метрическая матрица базисных контуров связанной сети имеет вид ^mC ^mC t = z` =

	6	7	8	9	10
6	3,0	1,0	1,0	1,0	0,0
7	1,0	3,0	0,0	0,0	1,0
8	1,0	0,0	3,0	1,0	1,0
9	1,0	0,0	1,0	3,0	0,0
10	0,0	1,0	1,0	0,0	3,0

Обращая полученную матрицу z` , и умножая ее слева на <sup>m</sup>C t , а справа на <sup>m</sup>C , получим матрицу решения Y c = <sup>m</sup>C t (z`)^{-1 m}C =

1         2         3         4         5         6         7         8         9        10

1	0,6216	-0,1081	0,1622	0,1622	0,1892	0,2162	-0,0541	0,2162	0,1892	-0,0541
2	-0,1081	0,5405	0,1892	0,1892	0,0541	-0,0811	0,2703	-0,0811	0,0541	0,2703
3	0,1622	0,1892	0,5495	-0,1171	-0,0811	0,2883	0,2613	-0,0450	-0,0811	-0,0721
4	0,1622	0,1892	-0,1171	0,5495	-0,0811	-0,0450	-0,0721	0,2883	-0,0811	0,2613
5	0,1892	0,0541	-0,0811	-0,0811	0,4054	-0,1081	0,0270	-0,1081	0,4054	0,0270
6	0,2162	-0,0811	0,2883	-0,0450	-0,1081	0,4955	-0,2072	-0,1712	-0,1081	0,1261
7	-0,0541	0,2703	0,2613	-0,0721	0,0270	-0,2072	0,4685	0,1261	0,0270	-0,1982
8	0,2162	-0,0811	-0,0450	0,2883	-0,1081	-0,1712	0,1261	0,4955	-0,1081	-0,2072
9	0,1892	0,0541	-0,0811	-0,0811	0,4054	-0,1081	0,0270	-0,1081	0,4054	0,0270
10	-0,0541	0,2703	-0,0721	0,2613	0,0270	0,1261	-0,1982	-0,2072	0,0270	0,4685

Умножим эту матрицу решения на вектор воздействия, заданный предложением и спросом, и представленный источниками напряжения e, www.rypravlenie.ru

том 17 № 3 (52), 2021, ст. 1

1        2        3        4        5        6        7        8        9       10

300

200

100

350

50

0

0

0

0

0

В результате получим отклики, токи в ветвях контурной сети ^mi c .

1          2        3          4        5         6        7          8         9         10

247,297

163,514

96,396

263,063

51,351

56,306

40,090

139,640

51,351

123,423

В силу единичных сопротивлений, полученные токи в ветвях численно равны напряжениям на ветвях mic = mec. Это токи, которые должны быть аналогами потоков продуктов в логистической сети. Но полученные токи не соответствуют потокам продуктов, которые надо транспортировать от входа к выходу. Однако можно дополнить эти токи с помощью источников воздействий в ветвях маршрутов, используя двойственную сеть.

Однако здесь ситуация отличается от рассмотренной выше простой сети. Пусть имеются ветви производителей и ветви потребителей. В каждой отдельной ветви два узла. Когда производители связаны с потребителями через узел заземления, что означает баланс, т.е. все произведенное потребляется, то число узлов равно сумме ветвей плюс один. Такой граф-дерево, имеет только разомкнутые пути, а замкнутых путей нет. Ветви, которые соединяют выходы производителей с входами потребителей, добавляют контуры, не меняя число узлов. Таким образом, маршруты типологически добавляют замкнутые пути в сеть. Если добавить источники в маршруты, то они создадут необходимые дополнительные токи в ветвях, которые приведут суммарные токи к значениям, соответствующим потокам продуктов в логистической сети.

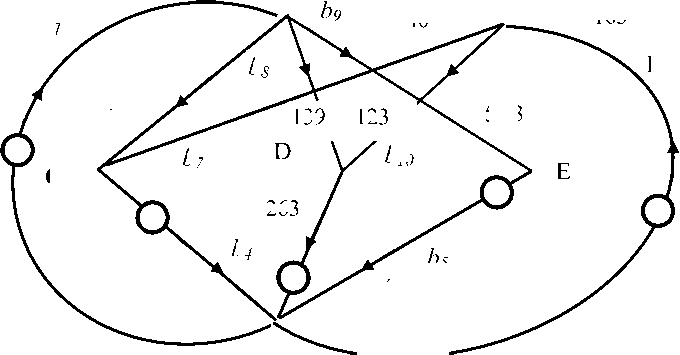
Результаты расчета контурной сетевой модели (токи, численно равные напряжениям в силу единичных сопротивлений), показаны на рисунке 4.

Ветвь поставки

A

В b1

e 1 = 300

b 8

D b10

b 7

b 4

Ветвь поставки b2

51,35

F

Рис. 4. Результаты расчета контурной сетевой модели транспортной системы

56,3

C

b 3

b 6

51,3

том 17 № 3 (52), 2021, ст. 1

Рассмотрим разности между заданными токами в простейшей сети и полученными в результате расчета. Эти разности рассматриваем как отклики в сети, которые дополнят токи на входе и на выходе так, чтобы суммарные токи в ветвях маршрутов соответствовали потокам продуктов от производителей к потребителям.

Ветви	1	2	3	4	5	6	7	8	9	10
ЭДС	300	200	100	350	50	0	0	0	0	0
Токи	247,30	163,51	96,40	263,06	51,35	56,31	40,09	139,64	51,35	123,42
Разности	52,70	36,49	3,6	86,9	-1,35	-56,31	-40,09	-139,6	-51,35	-123,4

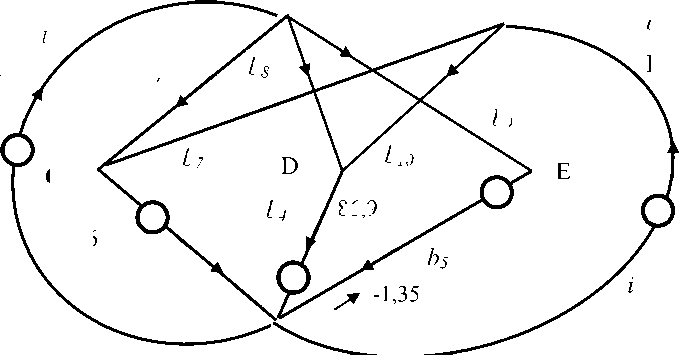
Полученные разности также соответствуют токам в двойственной сети в соответствии с инвариантом двойственности. Дополнительные токи в сетевой модели, они же токи в двойственной сети, показаны на рисунке 5,с индексом d , например, i¹ c d = 52,7 . Показаны токи ветвей входа и выхода, а дополнительные токи в маршрутах надо рассчитать.

Ветвь поставки

b 1 i¹ c d = 52,7

A

В b2

e 1 = 300

b 8

b 10

b 7

86,9

b 4

Ветвь поставки

36,49

F i1c d

Рис. 5. Дополнительные токи в контурной сетевой модели транспортной системы

b 6

?

b 9

C

3,6

b 3

Задача состоит в том, чтобы найти новые источники, отклики на которые дополнят токи в ветвях на входе и на выходе до значений реальных потоков поставки и спроса. Тогда в ветвях маршрутов суммарные токи дадут потоки перевозки продуктов от производителей к потребителям. В данном случае неизвестными являются дополнительные токи в маршрутах, в ветвях 6, 7, 8, 9 и 10. Эти ветви, в силу выбора путей, определяют базис контуров в структуре сети, а токи в них равны контурным токам.

Это значит, что источники напряжения в этих ветвях дадут дополнительные токи в ветвях, которые в сумме с уже полученными токами, будут соответствовать решению задачи транспортировки продуктов. Неизвестные дополнительные токи в маршрутах, в данном www.rypravlenie.ru

том 17 № 3 (52), 2021, ст. 1

случае, в ветвях 6-10, можно получить из условия баланса токов в узлах сети A, B, C, D и E по закону Кирхгофа. Баланс в узлах имеет следующий вид

Узел А: i¹ cd = i⁶ cd + i⁸ cd + i⁹ cd = 52,7.

Узел В: i² cd = i⁷ cd + i¹⁰ cd = 36,49.

Узел С: i³ cd = i⁸ cd + i¹⁰ cd = 3,6.

Узел D: i⁴ cd = i⁷ cd + i⁶ cd = 86,9.

Узел Е: i⁵ cd = i⁹ cd = -1,35.

Решая эту систему уравнений, обнаруживаем, что между неизвестными есть линейная зависимость. Это связано с балансом токов в узле заземления F, в котором сходятся потоки входа и выхода. Таким образом, надо задать один из токов, а остальные рассчитать из закона Кирхгофа в узлах сети. Например, зададим ток i7cd = 0, тогда получим остальные контурные токи, умножая на которые матрицу преобразования, получим дополнительные токи во всех ветвях сетевой модели. Заданное значение выделено жирным шрифтом. ic2 = mCt ikcd = ic1 + ic2

i c1

1	247,30
2	163,51
3	96,40
4	263,06
5	51,35	+
6	56,31
7	40,09
8	139,64
9	51,35
10	123,42

i c2

1	52,65
2	36,50
3	3,60
4	86,90
5	-1,35
6	3,60
7	0,00
8	50,40
9	-1,35
10	36,50

i c1 ⁺ i c2

1	299,95
2	200,01
3	100,00
4	349,96
5	50,00
6	59,91
7	40,09
8	190,04
9	50,00
10	159,92

	6	7	8	9	10	i c2
1	1,0	0,0	1,0	1,0	0,0		i7= 0	1	52,65
2	0,0	1,0	0,0	0,0	1,0			2	36,50
3	1,0	1,0	0,0	0,0	0,0			3	3,60
4	0,0	0,0	1,0	0,0	1,0	6	3,60	4	86,90
5	0,0	0,0	0,0	1,0	0,0	7	0,00	5	-1,35
6	1,0	0,0	0,0	0,0	0,0	8	50,40	6	3,60
7	0,0	1,0	0,0	0,0	0,0	9	-1,35	7	0,00
8	0,0	0,0	1,0	0,0	0,0	10	36,50	8	50,40
9	0,0	0,0	0,0	1,0	0,0			9	-1,35
10	0,0	0,0	0,0	0,0	1,0			10	36,50

Получим сумму токов в контурной сети и полученных дополнительных токов

Можно видеть, что суммы токов в узлах входа и выхода соответствуют заданным потокам спроса и предложения, которые распределились по ветвям маршрутов. Легко проверить, что сумма потоков по маршрутам равна сумме потоков на входе и сумме потоков www.rypravlenie.ru

том 17 № 3 (52), 2021, ст. 1

на выходе, а именно, равна 500, с учетом округлений. Вместе с тем возможны другие варианты, связанные с заданием требований по тем или иным маршрутам.

Например, если нужно обеспечить поток по ветви 6 равным 10, то получим следующее распределение потоков продуктов по данным маршрутам.

1 2	i c1	1 2	i c2	1 2	i c1 + i c2
	247,30		52,70		300,00
	163,51		36,50		200,01
3	96,40	3	3,60	3	100,00
4	263,06	4	86,95	4	350,01
i c1 + i c2     =   5	51,35	+          5	-1,35	=             5	50,00
6	56,31	6	10,00	6	66,31
7	40,09	7	-6,40	7	33,69
8	139,64	8	44,05	8	183,69
9	51,35	9	-1,35	9	50,00
10	123,42	10	42,90	10	166,32

Пусть дополнительный ток в ветви задан равным 100, то получим следующие результаты распределения потоков по данным маршрутам

ic1 ic2 ic1 + ic2 1 247,30 1 52,70 1   300,00 2 163,51 2 36,50 2   200,01 3 96,40 3 3,60 3   100,00 4 263,06 4 86,95 4   350,01 ic1 + ic2            5 51,35 +             5 -1,35 =              5    50,00 6 56,31 6 67,10 6   123,41 7 40,09 7 -63,50 7    -23,41 8 139,64 8 -13,05 8   126,59 9 51,35 9 -1,35 9    50,00 10 123,42 10 100,00 10   223,42 Таким образом, полученная сетевая модель и алгоритм расчета ее параметров, позволяют представить транспортировку потоков продуктов в логистической сети. Для анализа вариантов можно изменять выбор потоков в одной из ветвей, значения сопротивлений ветвей, и т.д. Обнуление потоков в отдельных маршрутах соответствует изменению выбора разных опорных планов. Вариации разных структур и разных параметров можно использовать для оптимизации плана перевозок. Можно сразу получить план перевозки при возникновении новых требований по объемам перевозок по тем или иным маршрутам.