Сетевое исчисление Network Calculus. Часть 1. Теоретические основы

С началом нового тысячелетия наметился активный переход от традиционных сетей связи с коммутацией каналов и временным мультиплексированием TDM (Time Division Multiplexing) к перспективным мультисервисным сетям следующего поколения NGN (Next Generation Network) [1]. В ближайшей перспективе Международный союз электросвязи прогнозирует построение будущих сетей FN (Future Networks) [2]. Общим для этих сетей является использование пакетных технологий для передачи любого вида информации (голоса, видео и данных) на базе протокола IP (Internet Protocol).

Для определения характеристик качества работы TDM-сетей используется часть классической теории массового обслуживания (ТМО) [3] – теория телетрафика [4], которая сыграла важнейшую роль при моделировании, анализе и расчете характеристик функционирования традиционных телефонных сетей. ТМО позволяет установить количественную связь между числом и типом приборов обслуживания, характеристиками входящего потока заявок и качеством их обслуживания. Например, в системах с очередями под качеством обслуживания, как правило, понимается своевременность обслуживания поступивших в систему заявок (среднее число заявок, находящихся в очереди на обслуживании; сред- нее время ожидания в очереди и т.д.). В системах без очередей основным показателем качества является вероятность отказа (блокировки) в обслуживании заявки.

Однако при попытке применить классическую ТМО к исследованию характеристик современных мультисервисных пакетных сетей возникает ряд трудностей. Во-первых, разнообразные заявки на обслуживание в таких сетях представляют собой пакеты различной длины, что является важным отличием от сетей TDM, где использовался, как правило, только один тип заявок – вызов или соединение. Во-вторых, обслуживание пользовательских пакетов в сетях NGN осуществляется в соответствии с различными методами обеспечения гарантий качества обслуживания QoS (IntServ, DiffServ и др.) с помощью таких механизмов, как профилирование – ограничение скорости потока пакетов пользователя в соответствии с выделенной ему полосой и шейпинг – сглаживание пульсаций трафика.

Все это значительно усложняет расчеты характеристик пакетных сетей при использовании методов классической ТМО. И, в-третьих, в большинстве международных рекомендаций (например, ITU-T Y.1541, ITU-T G.114, ITU-T G.1010, ETSI TS101329, 3GPP TS 22.105, 3GPP TS 23.107 и др.) для пакетных сетей указаны в качестве нормативных допустимые (максимально возможные) значения задержек, вари- аций задержек и потерь пакетов в зависимости от класса трафика, которые не всегда удается получить аналитически методами ТМО.

Кроме того, методы расчета характеристик пакетных сетей (пропускная способность каналов, емкость буферов, величина задержки, число потерянных пакетов и пр.), основанные на классической ТМО и которые с успехом использовались при анализе телефонных сетей, дают неоправданно оптимистические оценки QoS [5]. Объясняется это тем, что в пакетном трафике при сравнительно небольшом среднем значении интенсивности поступления заявок присутствуют относительно большие всплески нагрузки (так называемые пачечность, или берстность, трафика) и часто проявляется свойство самоподобия [6].

Математические модели, адекватно описывающие поведение современных мультисервисных пакетных сетей в целом и отдельных их узлов, существенно отличаются от широко известных моделей классической ТМО [7]:

– входной поток заявок имеет «взрывной характер», большие отклонения, что может означать возможность описания потока вероятностными распределениями, имеющими бесконечные математическое ожидание или дисперсию (так называемые длиннохвостные распределения);

– функционирование сетевых узлов в общем случае описывается нелинейными соотношениями «вход-выход», что может привести к невозможности адекватного подбора вероятностного распределения длительности обслуживания заявок в узле из числа известных;

– длина очереди в сетевом узле не является бесконечной, но может динамически ограничиваться для обеспечения некоторых заранее заданных гарантированных характеристик качества обслуживания QoS;

– дисциплина обслуживания в сетевом узле может динамически изменять как правила отказа требований в обслуживании, так и правила выбора требований на обслуживание в соответствии с некоторыми, заранее заданными, граничными значениями, обеспечивающими гарантированный уровень качества обслуживания QoS.

Таким образом, смена одного типа сетей связи на другой требует смены математических моделей и соответствующих методов расчета характеристик их функционирования.

Для исследования сложных пакетных сетей еще в начале 1990-х гг. был предложен качественно новый подход – теория Network Calculus (NC), позволяющая определять граничные оценки основных сетевых характеристик – загрузки сетевых узлов и задержки в передачи пакетов. Ее основной идеей является использование альтернативных методов анализа систем массового обслуживания: в частности, мин-плюс алгебры и макс-плюс алгебры, преобразование сложных нелинейных сетевых систем в линейные, которые легко исследовать аналитически.

Следует отметить, что термин «Network Calculus» не имеет устоявшегося русскоязычного аналога. Очевидно, что дословный перевод с английского network calculus как сетевое исчисление не отражает сути моделей, положенных в основу этой теории, поэтому приближенно названный термин можно охарактеризовать как «совокупность математических результатов для моделирования и исследования характеристик функционирования различных систем массового обслуживания (СМО), например телекоммуникационных сетей» [8]. Однако авторы все же остановились на термине «сетевое исчисление», который уже достаточно давно используется в отечественных научных публикациях, посвященных исследованию граничных характеристик различных сетевых моделей с применением теории NC [7; 9-11].

В предлагаемой первой части статьи приведены основные теоретические положения, современное состояние и перспективы развития сетевого исчисления . Во второй части планируется рассмотреть практические примеры использования NC для исследования различных инфокоммуникационных систем и сетей.

Базовые принципы теории сетевого исчисления

Прежде всего рассмотрим основные принципы теории сетевого исчисления NC и ее возможности для анализа характеристик функционирования телекоммуникационных сетей. Любая сеть связи описывается двумя основными понятиями: сетевыми узлами и потоками поступающих на них заявок (пакетов, вызовов, требований и т.п.) – см. рис. 1.

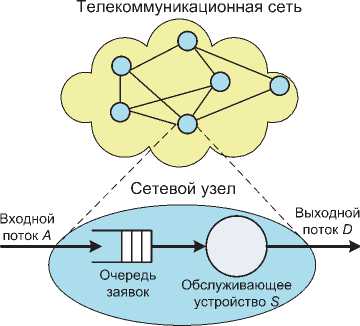
Рис. 1. Телекоммуникационная сеть и сетевой узел

Соответственно, любая теория сетевого анализа обычно строится на двух фундаментальных положениях: модель поступающего на узел трафика А и модель обслуживания этого трафика в узле S . При этом модель входного трафика А характеризует поведение входного потока заявок, а модель обслуживания трафика S характеризует поведение сетевого узла.

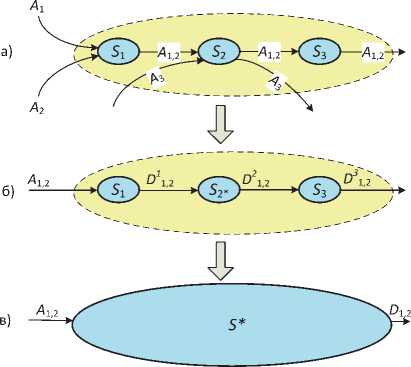
Рис. 2. Этапы анализа сети: а) исходный фрагмент сети; б) замена узла S ₂ на эквивалентный узел S ₂*; в) эквивалентная сеть в виде одного узла S *

Рассмотрим фрагмент (домен) сети, состоящий из трех узлов iS| • ^2 и трех потоков, как это показано на рис. 2а. Допустим, что потоки a_x и 7^2 _? описываемые соответствующими моделями, принадлежат к одному и тому же классу трафика и используют совместно один и тот же путь «из конца в конец» внутри рассматриваемого сетевого домена. На втором узле S' 2 имеется пересекающий кросс-поток ^3 , который использует ресурсы (пропускную способность) этого узла совместно с потоками A_x и Л₂. Предположим, что необходимо определить задержку из конца в конец в рассматриваемой сети для суммарного потока A_x э .

Можно использовать различные приемы анализа данной сети, но следующий подход является интуитивно наиболее простым [12]. Прежде всего для известных моделей трафика входных потоков A_x и моделей его обслуживания в узлах сети Sj возможен анализ функционирования одного узла с определением времени задержки прохождения трафика через него. Кроме того, анализ одного i -го узла также позволяет определить характеристики выходного потока этого узл а D с использованием модели входного трафика A,.

Этот выходной поток D, является входным для последующего (z + 1) -Г0 узла, что дает воз- можность многократного применения методики определения задержки в последовательной цепочке узлов. И, наконец, если потоки Ax и Аг (см. рис. 2а) принадлежат к одному и тому же классу трафика и совместно обслуживаются на одинаковых участках сети, основная идея предлагаемого подхода состоит в использовании объединенного потока ^1,2 на входе в первый узел

Как видно из рис. 2а, на втором узле объединенный поток ^1 2 конкурирует в обслуживании с кросс-потоком "^3 ■ Про стой подход для анализа этого узла – использовать эквивалентный узел ^ 2 для объединенного потока ^1 2 (см. рис. 2б). В этом эквивалентном узле на входе присутствует только объединенный поток, и в нем нет кросс-потока "^3 * Очевидно, что эквивалентный узел ^2 должен быть описан с использованием такой же модели обслуживания, что и исходный узел S* 2 • Таким образом, сеть преобразуется в совокупность эквивалентных обслуживающих узлов, для которых может быть проведен последовательный анализ от узла к узлу для получения величин задержек на каждом узле пути. Тогда общую задержку «из конца в конец» на всем пути можно легко получить суммированием отдельных задержек на каждом узле.

Однако, как будет показано далее, последовательный анализ узла за узлом можно значительно упростить, если использовать так называемое свойство сцепления. Суть его заключается в том, что последовательную работу (сцепление) узлов сети можно трактовать как один эквивалентный узел. Таким образом, с использованием свойства сцепления сеть в итоге можно заменить на один простой узел («черный ящик»), как это показано на рис. 2в. Применяя анализ для данного узла, получаем искомый результат величины сквозной задержки потока в сети, который может быть много лучше, чем результат, полученный последовательным анализом узла за узлом. Обобщая вышесказанное, можно сделать вывод, что в общем случае теория сетевого исчисления должна отвечать следующим пяти основным свойствам, чтобы с ее помощью можно было анализировать любую телекоммуникационную сеть [12].

Свойство №1 характеризует качество обслуживания. Для различных моделей потоков трафика и различных моделей обслуживания трафика в узле могут быть получены такие ха- рактеристики качества обслуживания, как число заявок в узле (загрузка узла) и задержка обслуживания заявок в узле.

Свойство №2 определяет характеристики выходного потока, см. рис. 3. Модель трафика выходного потока D узла с моделью обслуживания S может быть получена с использованием модели трафика входного потока A:A^^D.

Входной поток А

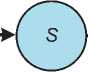
Выходной поток D

Обслуживающее устройство

Рис. 3. Характеристики выходного потока

Свойство №3 касается сцепления узлов, см. рис. 4. Сцепление (последовательное соединение) сетевых узлов может быть описано с использованием модели обслуживания, аналогичной модели для одиночного узла: 5/5^^.

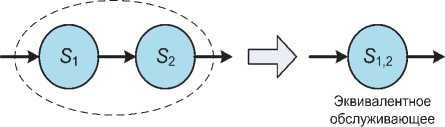
устройство

Рис. 4. Свойство сцепления

Свойство №4 характеризует остаточное обслуживание, см. рис. 5. Модель обслуживания потока в узле с конкурирующими кросс-потоками может быть получена с использованием модели обслуживания без конкурирующих кросс-потоков.

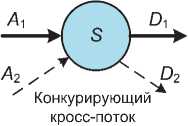
Рис. 5. Свойство остаточного обслуживания

Эквивалентное обслуживающее устройство

Свойство №5 – это свойство наложения (суперпозиции), см. рис. 6.

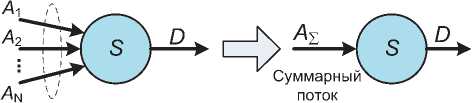
Рис. 6. Свойство наложения

Модель суммарного трафика нескольких потоков может быть получена с использованием исходных моделей трафика отдельных потоков. В классической ТМО многие модели СМО основываются на характеристиках потоков поступающих заявок и характеристиках их обслуживания в системе. Классическими примерами являются пуассоновский процесс поступления заявок и процесс обслуживания с отрицательным экспоненциальным распределением длительности обслуживания в одноканальной СМО М/М/1. В ТМО имеется множество результатов для систем с одним узлом обслуживания, которые соответствуют свойству №1. Имеется также много результатов для классических систем с очередями, соответствующих свойству №5, в частности когда источники заявок независимы. Например, при объединении двух пуассоновских потоков поступления заявок, если они независимы, результирующий поток будет соответствовать новому пуассоновскому процессу поступления заявок. При определенных условиях можно считать, что выходной поток в системе М/М/1 имеет пуассоновский закон распределения заявок в соответствии со свойством №2. Однако в общем случае выходной поток может иметь закон распределения заявок, отличный от модели входного потока. Более того, в классической теории очередей многие практические случаи не соответствуют также свойствам №3 и №4. Это частично объясняет, почему сложно применить классическую ТМО к анализу современных мультисервис-ных пакетных сетей. Основные отличия классической ТМО и теории NC приведены в таблице 1.

Таблица 1. Основные отличия ТМО и NC

Принципы классической ТМО	ПринципыNC
Один узел	Сеть узлов
Предположение о независимости событий	Общий случай
Единицей обслуживания является заявка	Единицей обслуживания является пакет. Заявкой является поток, состоящий из множества пакетов
Мало моделей, в которых заявки могут объединяться и разделяться	Потоки объединяются (агрегируются) и разделяются
Простые виды трафика	Профиль трафика может быть сложным
Основная цель анализа -точность оценок исследуемых характеристик	Целью анализа является получение граничных оценок исследуемых характеристик

История возникновения и современное состояние теории NC

Основоположником теории NC является профессор Калифорнийского университета Р.Л. Круз (1959-2013), который опубликовал в 1991 г. две части своей статьи [13-14]. В первой части были рассмотрены характеристики различных сетевых элементов, таких как линия с постоянной задержкой, входной буфер, мультиплексор, демультиплексор и др. Основное внимание в этой и дальнейших работах Круза, а также его последователей уделялось ^с,р^ – регулятору трафика, аналогичному алгоритму «дырявого ведра», где параметр р характеризует скорость входного потока трафика, а о – его пачечность (берстность). Обусловлено это тем, что данный регулятор в наибольшей степени подходит для описания трафика современных пакетных сетей.

Основная идея предлагаемого метода анализа функционирования пакетной сети заключалась в определении взаимосвязи границ пачечности потоков трафика с характеристиками функционирования узлов в различных точках сети. Очевидно, что если поступающий ^■р} -трафик обслуживается сетевым узлом с производительностью р , то число пакетов в узле (загрузка узла) никогда не будет больше о . Другими словами, Круз доказал, что если трафик на входе в сеть имеет небольшую пульсацию (пачечность), то поток трафика внутри сети так же не слишком пульсирующий. Впервые количественная зависимость основных сетевых характеристик – числа пакетов в узлах (backlog) и задержки пакетов от пачечности и скорости поступающего в сеть трафика – показана Крузом во второй части статьи [14].

С момента создания теории сетевого анализа были разработаны два ее направления – детерминированное и стохастическое. Теория детерминированного сетевого исчисления DNC (Deterministic NC) применяется при исследовании сетей, предоставляющих гарантии детерминированного обслуживания для поступающих потоков заявок [15-16]. DNC может быть использована для исследования СМО, на которые поступает неизвестный трафик, но имеющий детерминированные границы максимального числа поступивших пакетов, а обслуживание поступивших пакетов в системе также осуществляется с детерминированными верхними границами производительности. К числу таких систем относятся локальные компьютерные сети, специализированные бортовые сети (например самолета), системы на кристалле и др. Детерминированные модели NC, в отличие от стохастических, более просты и понятны для восприятия. Основные положения DNC рассмотрены ниже.

Однако часто на практике процессы поступления и обслуживания заявок в СМО характеризуются стохастическим процессом, при этом требуется определенная вероятностная гарантия качества обслуживания QoS. Примером могут служить современные мультисервисные сети связи, обслуживающие мультимедийные потоки для передачи голоса, видео и данных. Для анализа и обеспечения гарантий качества обслуживания в таких системах и сетях в наибольшей степени подходит теория стохастического (случайного) сетевого исчисления SNC (Stochastic NC) [12], основные положения которой будут представлены далее.

Теоретическим исследованиям сетевого исчисления и различным аспектам его практического применения посвящены многочисленные научные публикации – монографии, статьи, диссертации. Развитие теории NC в последние годы привело к появлению новых ее приложений и созданию выделенных направлений исследований, таких как статистическое (Statistical NC) [1718], сенсорное (Sensor NC) [19-20], временнóе (Temporal NC) [21], беспроводное (Wireless NC) [22-23], а также использование сетевого исчисления для анализа не-FIFO систем [24-25], систем с потерями [26-27], call-центров (SLA Calculus) [28] и др. Анализу этих и других направлений практического применения NC будет посвящена вторая часть настоящей статьи.

Следует отметить, что в настоящее время теория NC уже входит в программы подготовки бакалавров и магистров в ряде университетов. Так, специальный курс Network Calculus читается в Королевском технологическом институте (Стокгольм, Швеция) [31]. В Университете имени Бар-Илана (Рамат-Ган, Израиль) в учебном курсе «Коммуникационные сети» несколько разделов посвящены изучению теории детерминированного и стохастического сетевого исчисления [32]. Лекционный курс по стохастическому NC включен в программу Берлинской математической школы [33]. На факультете вычислительной математики и кибернетики МГУ читался магистерский курс «Компьютерные сети и телекоммуникации (дополнительные главы)», в котором есть раздел «Введение в сетевое исчисление» [34].

Сегодня известны несколько программных пакетов, реализующих разделы общей теории сетевых исчислений и связанных с этим моделей и методов исследований. К ним относятся такие программы, как CyNCtoolbox на основе пакета Matlab/Simulink, RTC toolbox в среде Matlab, DISCO network calculator на Java, COINC toolbox и DEBORAH на языке C++, SymTA/S toolbox и др. Краткий обзор этих и других программных средств моделирования и анализа различных моделей методами теории NC приведен в [35].

Все вышеперечисленное говорит о том, что теория NC активно развивается и является перспективным направлением моделирования и исследования сложных сетей и систем.

Математическая основа NC

Математической основой сетевого исчисления является относительно новый раздел математики, который сейчас принято называть идемпотентной математикой (часто называемой тропической в честь заслуг бразильского математика Имре Шимона) [36]. Это направление в математике активно развивается многими авторами, в нашей стране наиболее важные работы ведутся научной школой под руководством академика В.П. Маслова [37].

Термин «идемпотентность» означает свойство математического объекта, которое проявляется в том, что повторное действие над объектом не изменяет его, например, Х + Х = X, каков бы ни был элемент x . В основе идемпотентной математики лежит замена обычных арифметических операций новым набором базовых операций (такими как максимум max или минимум min), при этом числовые поля заменяются идемпотентными полукольцами и полуполями [38].

Типичные примеры – так называемые идемпотентные алгебра max-плюс R max и алгебра min-плюс R min . Пусть R – поле вещественных чисел. Тогда ^max – диоид (Ru{-oo},v,+) с операциями x v у = max{x, v} и xxy = x + y, то есть в идемпотентной алгебре новое сложение равно максимуму, а новое умножение совпадает с обычным сложением. Аналогично

^Rmin – диоид (R о {+co}₅a₉+) с операциями x a v = min{x, у} и xxy = x + y. Алгебры ^R max ^{И R}min являются диоидами, так как в них определены по две операции.

В теории электрических цепей с помощью математической операции свертки входного сигнала x ( t ) и импульсной характеристики h ( t ) линейной системы может быть получен выходной сигнал этой системы:

В теории NC входному сигналу сопоставляется кривая входного потока, а импульсной функции – кривая обслуживания (понятия этих кривых приведены далее). Поэтому аналогично выходной поток СМО может быть получен сверткой функции входного потока и функции обслуживания системы. Но так как в (min,+)-алгебре операция «сложение» представляет собой операцию нахождения минимума, поэтому операция (min,+)-свертки двух функций f ( t ) и g ( t ) (обозначается символом ® ) представляет собой функцию

• (/ ® g)(t) = inf {/(? - 5) + g(5)} . (2) 0< s

Двойственной операцией для операции (min,+)-свертки является операция (min,+)-обрат-ной свертки (развертки) функций f и g (обозначается символом о ), которая представляет собой функцию

• (/ ⁰ gXO = ^p{f(t + u) - g(w)}. (3) и > 0

Соответственно, в (max,+)-алгебре для нахождения свертки функций используется супремум, а для развертки – инфимум.

Замена свертки вычислением инфимума или супремума в идемпотентных алгебрах значительно упрощает нахождение результирующей функции, что широко используется в теории NC при анализе различных сетевых моделей.

Основную парадигму идемпотентной математики выражает идемпотентный принцип соответствия [36]. Этот принцип тесно связан со знаменитым принципом соответствия Н. Бора для квантовой теории. Оказывается, существует эвристическое соответствие между рядом важных, интересных и полезных конструкций и результатов обычной математики над полями и аналогичными конструкциями и результатами над идемпотентными полуполями и полукольцами

(полуполями и полукольцами с идемпотентным сложением). Иначе говоря, идемпотентная математика является асимптотической версией традиционной математики над полями вещественных и комплексных чисел. Точно так же, как классическая механика проще квантовой, так и идемпотентная математика проще обычной. Поэтому основная задача состоит в том, чтобы найти способы применения новой математики для решения традиционных задач: например, по анализу характеристик сложных телекоммуникационных сетей. Однако следует учитывать, что переход от традиционных конструкций и результатов к их идемпотентным аналогам часто является нетривиальным.

Основные положения DNC

Модель сетевого узла в терминах NC представлена на рис. 7.

^4(0

Рис. 7. Модель узла сети в теории NC

>ОД

Пусть входящий в узел поток трафика характеризуется кумулятивной функцией (кривой) A ( t ). Поток обслуженных пакетов на выходе узла с функцией обслуживания PW характеризуется кумулятивной функцией (кривой) D ( t ). Рис. 8 иллюстрирует пример этих кривых при постоянной скорости обслуживания в узле P^ = R. Когда система свободна, кривые этих потоков совпадают. Всякий раз, когда система загружена, она передает данные на выход со скоростью R , которая определяет угол наклона кривой D ( t ).

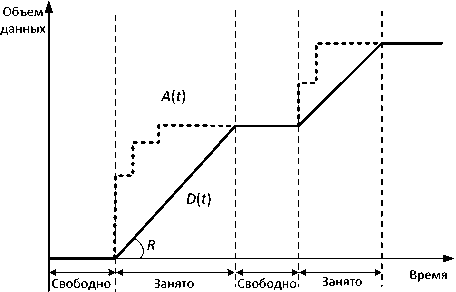
Рис. 8. Пример кривых (функций) входящего потока A ( t ) – штриховая линия; и выходящего потока D ( t ) – сплошная линия

Основная идея теории детерминированного сетевого исчисления состоит в том, что гранич- ные значения характеристик качества обслуживания потоков трафика в сетевом узле можно получить c использованием известных кривых детерминированных функций A(t) и D(t) [16]. В частности, верхнее граничное значение задержки потока трафика в узле d определяется как максимальное горизонтальное расстояние между кривыми A(t) и D(t):

d(A,D) := sup(inf[<7 e R⁺ ,D(t + d) > Л(/)]), t>0

где R – множество неотрицательных чисел. Граничное значение загрузки узла (числа пакетов в узле) b определяется как максимальное вертикальное расстояние между кривыми A ( t ) и D ( t ):

b(A, D):- sup(v4(?) - D(fp.

/>0

В общем случае для вычисления значений характеристик QoS в СМО необходимо задать законы, описывающие поступающий поток трафика и дисциплину его обслуживания в узле. Для этих целей в NC используются кривая поступления a(t), описывающая входящий в узел поток трафика, и кривая обслуживания PQ^, описывающая процесс обслуживания этого потока в узле.

Функция aUA будет являться кривой поступления для потока трафика на входе узла при условии, что для некоторого наблюдаемого периода времени [0, t ] выполняется следующее неравенство:

A(t) - A(s) < a(t - s), 0 <  s < t.

Следовательно, действительное число поступивших пакетов в потоке будет всегда меньше или равно числу пакетов, определяемых на основе кривой поступления a(P, то есть она определяет наименьшую верхнюю границу числа пакетов в поступающем потоке.

Функция PkP является кривой обслуживания для узла при условии, что для некоторого наблюдаемого периода времени [0, t ] число пакетов в выходном потоке D ( t ) в момент времени t удовлетворяет неравенству:

D(O > inf[^(Z - 5) + ^(s)] = (A ® PXp ;

0 < s < t, где ® – символ (min,+)-свертки.

По аналогии с кривой поступления функция (кривая), описывающая поток трафика на выходе узла /(0, может быть определена как:

y(t) = a(t)* P(t), где * – символ обычной свертки.

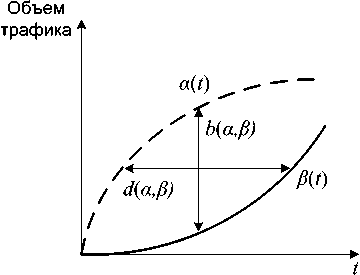
Рис. 9. Граничные значения задержки пакетов d(a,p\ и загрузки узла b(a,P)

Следовательно, граничные значения задержки пакетов в узле и загрузки узла будут определяться, соответственно, как максимальные горизонтальное и вертикальное расстояния между кривыми a^ и PU^ – см. рис. 9.

Важнейшим свойством DNC является расширение концепции кривой обслуживания от отдельного узла до произвольного числа последовательно включенных сетевых узлов [16]. Это позволяет получить сквозные характеристики всей сети с использованием методики оценки граничных характеристик для одного узла. Так, поток на выходе двух последовательно работающих узлов сети с кривыми обслуживания PPP и p^ соответственно, может быть определен путем рекурсии D^>(A®p^®p₂(tY Поскольку (min,+)-свертка является ассоциативной операцией, можно записать D^>A®{p_{®P₂\p.

Отсюда в общем случае сеть, состоящая из N последовательных узлов с кривыми обслуживания Pi, i-V-,N (рис. 10), эквивалентна одному узлу с кривой обслуживания pneAf) = P®P2®---®PN(P, где Pnet называется кривой обслуживания сети. Из-за коммутативности (min,+)-свертки порядок узлов не оказывает влияния на кривую обслуживания сети, например, конкретное местоположение самого узкого места в сети с точки зрения пропускной способности (так называемое бутылочное горлышко) не имеет значения для анализа, а важна только величина этого «горлышка».

Dpt)=A2^ = Д®Р1(Г) 02(^)⁼^2® P?(f) ⁼ ^(^Pl^S^U)

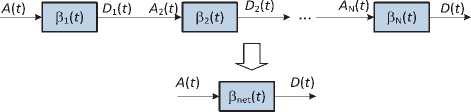
Рис. 10. Преобразование последовательности сетевых узлов

Особая ценность модели кривой обслуживания узла заключается в том, что она позволяет учесть различные алгоритмы обработки трафика в узле (профилирование, планирование, приоритетность, ограничение и др.). С этой целью введено понятие остаточной функции (кривой) обслуживания узла [15]. Если узел без потерь с дисциплиной FIFO имеет кривую (функцию) обслуживания p^ и на него поступает два потока с кривыми поступления a_x(p ^и «А*Р то остаточные кривые обслуживания этого узла для первого P_xQ,n и второго PAt,^ потоков в момент времени t определяются как:

P\ V, t) = VP(A ~ a₂ V - r)]⁺ • l_!?>r,;

P2(t,T) = VP(t)-apt-T)A+ A^t>lV где ^>r; – индикаторная функция, M+ обозначает max{0, x}.

Использование свойств остаточного обслуживания позволяет с помощью DNC проводить анализ различных схем обслуживания трафика в сложных сетевых моделях.

Одним из базовых принципов в DNC также является принцип «плати за берстность один раз» PBOO (Pay Burst Only Once) [39], определяющий правила эффективной композиции обслуживающих узлов. Суть принципа заключается в том, что оценка задержки передачи в последовательности сетевых узлов (см. рис. 10), полученная с помощью простого суммирования, проигрывает в точности оценке, полученной в результате предварительного вычисления общей кривой обслуживания сети. Причины такой разницы заключаются в том, что поузловая оценка задержки учитывает берстность проходящего через сеть потока в каждом узле. Принцип PBOO позволяет избавиться от указанных изъянов, учтя берст-ность потока единственный раз в первом узле.

Основные результаты DNC справедливы для обслуживающих узлов и потоков данных, кривые обслуживания и поступления которых описаны произвольными детерминированными функциями. В то же время для решения множества практических задач может быть удобным наложить дополнительные ограничения и аппроксимировать эти кривые известными функциями. В частности, кусочно-линейные функции удобны при описании работы алгоритма «дырявое ведро» [39].

Основные положения SNC

Главным недостатком DNC является то, что оно позволяет получить детерминированные границы качества обслуживания, которые осно- вываются на наихудшем случае. Однако в большинстве практических случаев входные потоки трафика и обслуживающие устройства характеризуются некоторыми стохастическими процессами, и использование для них детерминированных моделей приводит к слишком завышенным требованиям к сетевым ресурсам для обеспечения детерминированных гарантий QoS. Так, из определения (ст, /?) -кривой поступления следует, что любые «всплески» (берстность) трафика повышают требования к пропускной способности независимо от вероятности их появления, что приводит к неэффективному использованию сетевых ресурсов при передаче мультимедийного трафика. Кроме того, линейная зависимость кривой поступления от количества потоков препятствует реализации статистического мультиплексирования, что особенно сильно сказывается на эффективности использования ресурсов многоканальных транспортных сетей.

Стохастическое сетевое исчисление SNC (Stochastic NC) [40] позволяет получить оценку того, что реальные значения параметров QoS не будут превышать граничные величины с некоторой вероятностью меньшей единицы:

/’{Реальное QoS > Требуемое QoS} < £ , где s – допустимая вероятность, с которой реальное качество обслуживания QoS нарушает гарантированные границы.

Основой SNC являются стохастические кривые поступления и обслуживания. Говорят, что поток имеет стохастическую кривую поступления а, учитывающую объем трафика, с граничной функцией f , если для всех О < 5 <  t и всех х > О имеет место неравенство

P{A(s,t)-a(t-s) >  х} <  рУУ

Для анализа характеристик стохастического обслуживания представлено множество стохастических моделей. Например, для WYp^Y модели стохастическая кривая поступления заявок имеет граничную функцию е ^&, где 9 – некоторый заданный параметр [12]. Говорят, что система имеет стохастическую кривую обслуживания Р с граничной функцией g , если для всех t > 0 и .г > О справедливо неравенство

P{Sup[^®/?(0-W)]>x}

РУ(1) > х} < / ® g(x -а ° Р(0Р и

РУ^ > Ца + х,РУ® g(x), где о – символ обратной (min,+)-свертки (развертки); h(a + х, Р) – максимальное горизонтальное расстояние между функциями cpt> + х и /?(0 для х > 0.

Следует отметить, что в последние годы SNC стала привлекательной методологией для получения вероятностных граничных оценок характеристик различных СМО. Теория SNC основывается на том, что известны точные вероятностные характеристики процессов поступления и обслуживания заявок в системе. Однако на практике во многих случаях затруднительно, если вообще возможно, сделать такие априорные предположения. Более практичным является подход, при котором операции в SNC основываются на реальных измерениях (желательно даже онлайн) процессов поступления и обслуживания заявок в системе. Это направление развития SNC для моделирования сетей с минимумом априорных предположений получило название статистического NC (StatNC) [17]. Основное внимание исследователей в рамках теории StatNC направлено на оценку точности получаемых граничных значений характеристик систем.

Нерешенные задачи и проблемы

Наряду с достигнутыми успехами в теории сетевого исчисления остаются еще открытыми вопросы и проблемы, которые требуют своего разрешения в следующих областях:

• 1.    Сетевая топология. Замечательным свойством сетевого исчисления является возможность анализа различных систем, которые могут быть составлены из произвольных сетевых топологий. Однако разработанные аналитические и численные методы ориентированы в основном на линейные топологии с последовательной (feedforward) передачей потоков трафика. Для других классов топологий (с обратной связью, кольцевых, вложенных и др.) требуется определить их характерные свойства и разработать соответствующие методы их анализа в теории NC.

• 2.    Параллельные системы. Оценка производительности параллельных систем в последнее время приобретает все более важное значение в

• 3.    Беспроводные радиосистемы. При анализе беспроводных сетей интересным является вопрос, как стохастические свойства радиоканалов влияют на задержки информации в канале и его загрузку. Обычные статистические модели передачи радиосигналов в беспроводной среде трудно использовать в моделях ТМО. В связи с этим весьма эффективными и перспективными являются последние результаты в области сетевого исчисления, полученные для радиоканалов с замираниями.

• 4.    Преобразования потоков трафика. Большой сложностью для существующих методологий анализа систем массового обслуживания является учет преобразований трафика, которые происходят в мультисервисных сетях, например в случае транскодирования видео- или аудиопотоков. Несмотря на определенный прогресс для специальных элементов масштабирования в теории NC, который достигнут в последние годы, есть еще много открытых вопросов. Важность этой проблемы очень велика, так как ее решение значительно расширит область исследования сетевого исчисления для современных сетей.

• 5.    Точность получаемых граничных оценок. Основываясь на способности решать некоторые фундаментально сложные задачи массового обслуживания, стохастическое NC рассматривается как полноценная альтернатива классической ТМО. Для определения граничных характеристик в стохастическом сетевом исчислении часто используются хорошо известные оценки распределений, такие как границы Чернова и другие. Однако точность этих границ является актуальной темой для дальнейших исследований.

• 6.    Конечные буферы. Типичным и удобным предположением в сетевом исчислении является то, что буферы очередей считаются бесконечными. Однако представляет значительный интерес разработка новых моделей NC, которые могли бы учитывать конечные размеры буферов.

связи с распространенностью параллельных вычислительных моделей в таких перспективных технологиях, как дата-центры, облачные вычисления, умные энергосети (smart grids) и др. Таким образом, имеется прекрасная возможность для теории сетевого исчисления при разработке новых моделей и методов, которые позволят более фундаментально и глубоко исследовать характеристики параллельных систем.

Выводы

Сетевое исчисление Network Calculus становится универсальной методологией анализа раз- личных систем и сетей массового обслуживания. Перспективность данного подхода заключается в том, что он позволяет решать задачи, которые являются сложными для других методик, так как оперирует с граничными оценками исследуемых характеристик, а не стремится получить их точные значения. Высокая моделирующая способность сетевого исчисления совсем недавно была продемонстрирована на практике при решении традиционных для Internet инженерных сетевых задач, связанных с оценкой качества обслуживания QoS на основе технологий IntServ и DiffServ, а также при анализе различных сетей и систем массового обслуживания, таких как беспроводные сенсорные сети, коммутируемый Ethernet AFDX, системы-на-кристалле, умные энергетические сети (smart grids), виртуальные частные сети VPN и др. [41]. Анализ этих и других примеров практического применения сетевого исчисления в различных предметных областях приведен во второй части статьи.

Достигнутые успехи в теории NC позволяют прогнозировать, что пройдет определенное время и перечисленные выше нерешенные теоретические и практические задачи и проблемы найдут свое эффективное разрешение. Хочется надеяться, что отечественные ученые и исследователи примут в этом процессе самое активное участие и внесут свою лепту в развитие и использование на практике моделей и методов теории сетевого исчисления.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-00363 мол_а «Исследование и разработка математических моделей и методов анализа виртуальных частных сетей на основе теории Network Calculus».