Сети дискретных операторов

Системы неоднородной структуры широко распространены на практике и в настоящее время являются предметом активного изучения представителями различных научных школ и направлений. К ним традиционно относят дискретно-непрерывные, логико-динамические, гибридные и гетерогенные динамические системы, а также системы с переменной структурой. В данной работе рассматриваются системы неоднородной сетевой структуры. Для их моделирования и исследования применяется иерархический подход: строится двухуровневая модель, нижний уровень которой представлен различными управляемыми дискретными системами однородной структуры, а верхний — сетью операторов, обеспечивающей целенаправленное взаимодействие дискретных подсистем. Эту модель можно рассматривать как дальнейшее развитие неоднородной дискретной модели, предложенной и исследованной в ряде работ авторов [1, 2] . Ставится задача оптимального управления, и приводятся достаточные условия оптимальности управления — аналоги известных достаточных условий оптимальности Кротова [3] , в которых фигурируют разрешающие функции типа Кротова для каждого уровня.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований: проекты № 15-01-01915_a , № 15-01-01923_a, № 15-07-09091_a.

○c Программные системы: теория и приложения, 2016

Рис. 1.

• 1.    Сеть операторов и достаточные условия оптимальности

Пусть имеется N операторов произвольной природы Д : Х к x U ^ Y k ,

• (1)                            У к = / ^{( к,х} к ^,и к ).

Вводятся подмножества Х к _д , такие что Н” = 1 Х кд = Х к .

Говорят, что выход оператора I подается на вход оператора к, если для некоторого q имеет место равенство х(к^,х к ) = y i , где х(к, q,х _k ) — оператор проектирования на подмножество X _kg .

Пусть рассматриваемые операторы соединены указанным образом по некоторой схеме, представляемой ориентированным графом (рис. 1) .

Предполагается, что для данного к между номерами q и I имеет место взаимно-однозначное соответствие.

Иными словами, X k олицетворяет множество входов к-го оператора, занятых в соединениях, а U _k — множество свободных входов. Такая модель называется сетью операторов . Специальный случай сети — цепочка произвольных операторов — может рассматриваться как общая модель динамической системы с переменной структурой.

Рассматривается задача о минимуме функционала

N       N              N

• (2)    I = £ 1 к (_Ук) = £ Mf (к,х к ,и _к )) = £ / 0 (к,х к ,и _к ) 11    1

на множестве D наборов т = { (х к , и к ) } , к = 1,..., N, связанных указанными соотношениями сети и возможными дополнительными ограничениями вида (х к , и к ) € В (к), где В (к) — заданное при каждом к множество. Требуется найти минимизирующую последовательность { m _s } С D , т.е. такую, что I(m _s ) ^ inf I .

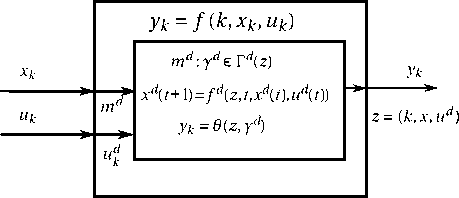
Рис. 2.

Вводится множество E элементов т, не связанных сетевыми условиями — равенствами x(k,j , x _k ) = U i . Строится обобщенный лагранжиан:

N

L = -]Т R(k,xk ,ик), k=1

N

• (3)    ^{R ( k,x,u}) = ^(^(kJJ ^{( k,x,}u)) - Ф ⁽ 1, к, x ^{( k,l,x )))} - / ^{0 ( k,x,u )} , 1=1

• 2.    Двухуровневая модель с обыкновенными дискретными системами

где ^(к, l, y k ), k,l = 1,... , N — произвольные функционалы, такие что ^(к, 1,у к ) = 0, если равенство x(k,j,x k ) = y i отсутствует (отсутствует связь l ^ k).

Теорема 1. Пусть имеются последовательность { m _s } С D и функционалы ^(k,l,y k ) такие, что R(k,X k _s ,U k _s) ^ ^(k), k = 1,..., N , где ^(k) = sup { R(k, x, и) : (x, и) e B (k) } .

Тогда { m _s } минимизирует функционал I на D .

Доказательство теоремы и первый вариант модели сети операторов даны в [4] .

Предлагается следующая конкретизация абстрактной сети операторов (рис. 2) .

Представим условие (xk,Uk) e B(k) в форме xk e X(k), Uk e U(k,!k), где X(k) — проекция на Xk, U(k,xk) — сечение B(k) при данных k, xk. Пусть на некотором подмножестве K’ С K = {1,...,N} имеем и = (и, md), где ud — произвольной природы, а md — некоторый дискретный управляемый процесс, так что сечение множества U(k, x) при фиксированных x и х есть допустимое множество Dd(k,x, и) с соответствующей дискретной системой

• (4)                x ^d (t +1) = f^d(z, t, x ^d (t),u ^d (t)), t G T (z),

x ^d G X ^d (z,t) C R ^{n ( k )} , u ^d G U ^d (z,t,x ^d ) C R ^{p ( k )} , z = (k,x,x).

^ ^d = (t z ,x ^d , t _F , x F ) G { 7 ^е : t j = т(z),x^d = ^(z), t _F = ^(z), x F G r ^d (z) } . Решением этой комбинированной системы будем считать набор т = (x(k), u(k)) G D , где при k G K ‘ : u(k) = (x(k), m ^d (k)), m ^d G D ^d (t, x(k), u ^d (k)).

Задача оптимизации формулируется для верхнего уровня. Требуется минимизировать функционал (1) . Рассматривается множество E элементов m, не связанных сетевыми условиями — равенствами x(k,j,x . ) = y i и дифференциальными связями нижнего уровня. Вводятся произвольные функционалы v(k,l,y . ), k,l = 1,..., N , такие что V(k, l,y _k ) = 0, если равенство x(k,j,x _k ) = y _i отсутствует (отсутствует связь l ^ k).

Для номеров k G K ’ вводится дополнительно функционал V ^d (z,t, x ^d ) Основные конструкции достаточных условий оптимальности имеют следующий вид [2] :

где У к = 9 (z, 7^d) при к Е К ’ , у к = / (к, x, и) при к Е К \ К ‘ . Обозначим № = sup { G ( z, 7 ^d ) : 7 ^d Е Г (z) } , x d Е X ^d (z, t j ), x ^d _F Е X ^d (z,t _F ), u ^d Е U ^d (k), x Е X (k).

Легко убедиться, что L(m) = I(m) при m Е D , т.е. при выполнении отброшенных связей. Для этого рассмотрим вначале выражение для функции R ^d . При выполнении рекуррентной цепочки (4)

R ^d (z, t, x ^d , u ^d ) = / (z, t + 1, x ^d (t + 1) ) - / (z, t, x ^d (t) ⁾ .

Тогда t p — 1

• - E R ^d (z) + V^d (z, ti,x^d) - / (z, t_F,x^d_F)) = t l

t p — 1

• - E (v^d (z , t + 1, x ^d (t + 1) ) - _V ^d ( z, t, x ^d (t)) + _V ^d ( z, t i ,x) - t l

t p — 1

- V ^d (.z, tF, x ^dF ) = - ^ (v ^d (^z, t, x ^d (t)) - _V ^d (p t, x ^d (t) ) ).

t l

С учетом выполнения сетевых связей %(k, j^x k ) ) = у / получим:

N

^ ^ ^R k EE ^{m (} V ^{( k,}l^,y k ^{) -} V ⁽ l^,k,y i ⁾⁾⁺ K ‘          K ‘ 1 = 1

t p 1                            t p 1

+ E ^ ^d (z,t) - I k (у к ) - ^ M ^d (z,t). t l                                         t l

Тогда

N

E R k = E E( ^(k, ^l, У к ) - v(l, k, y i )) - I k (У к ). K'         K' 1 = 1

Окончательно имеем:

Теорема 2.

• 1.    Для любых p, p ^d и т Е D имеет место оценка

• (5)      I(т) — I * <  Л = L(m) — L * , I * = inf I, L * = inf L.

• 2.    Пусть имеются два элемента т¹ Е D и т¹¹ Е E и функциона

лы p и p ^d , такие, что L (т¹¹) < L (т ¹) = I (т¹) , и т ¹ Е D .

Тогда I (т ¹¹ ) <  I(т¹}.

Теорема 3. Пусть имеются последовательность элементов { rn _s } С D и пара (p, p^d) такие, что:

• 1)    R (k, x _s (к) , u _s (к)) ^ р (к);

t p 1

• 2)    Е ( R ^d ( z _s (k),f,T ^d (k,t) ,U ^d (к,!)) — p ^d (z _s (k),t)' ) ^ 0, к Е K ‘ ; t j

• 3)    G (z: _s (k),p d (k) ) — P (к) ^ 0, к Е K ‘ .

• 3.    Заключение

Тогда последовательность { т ₈ } — минимизирующая для I на D .

Доказательства теорем 2 и 3 аналогичны приведенным в [2] . Сформулированные достаточные условия позволяют строить конкретные методы и алгоритмы оптимизации.

В работе представлена иерархическая модель сети дискретных операторов, для которой поставлена задача оптимального управления. Даны достаточные условия оптимальности типа Кротова.