Сети Петри с памятью состояний

Математический аппарат сетей Петри с момента своего появления зарекомендовал себя как достаточно универсальное средство моделирования процессов различной природы и сложности [1, 2]. Динамика сети Петри отражается в изменении количества маркеров в позици-

Описание предлагаемого метода

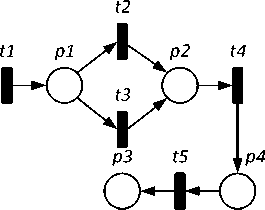
Обобщенная сеть Петри (рис. 1) формально описывается набором вида

R = {P,T,D,μ0}, где P = {p} - непустое конечное множество позиций, i = 1, n; T = {^i} - непустое конечное множество переходов, j = 1, m; D = D + — D- — отношение инцидентности позиций и переходов; μ0 : P → R+ – начальная маркировка сети; R+– множество целых неотрицательных чисел; n – ко-0

личество позиций; m – количество переходов.

Матрица инциденций позволяет определить уравнение, формирующее механизм изменения маркировки сети:

μ[k = 1] = μ[k] = D ∙ u[k], где u[k] – вектор-столбец длины m, имеющий единственный ненулевой элемент в позиции j, равный 1 и, соответственно, определяющий, какой из переходов срабатывает на текущем такте управления.

Условие срабатывания переходов сети имеет следующий вид:

D ^– ∙ u [ k ] ≤ μ[ k ].

Предлагается реализовать в сети дополнительный вектор маркировки, который будет отображать предысторию изменения маркировок позиций. Вводимый вектор можно охарактеризовать как статическую маркировку сети, а стандартный вектор маркировки – динамическую маркировку. Формально, исходя из вышеизложенной идеи, элементы вектора статической маркировки должны накапливать маркеры в каждой позиции на каждом такте имитационного эксперимента.

Уравнение состояния должно предусматривать изменение каждого вектора маркировки:

ц [ k + 1] = ц [ k ] + D ■ u [ k ] z [ k + 1] = z [ k ] + ц [ k + 1]^,

где μ[ k ], μ[ k + 1] – стандартный (динамический) вектор маркировки; z [ k ], z [ k + 1] – введенный (статический) вектор маркировки.

Основным вопросом с точки зрения организации управления является вопрос использования сформированного вектора статической маркировки. Возможны разные варианты такого использования: ограничение количества маркеров в позициях (s-ограниченность), ограничения маркировки группы позиций или применение дополнительного классификатора состояний [3]. Приведем простой пример его использования для управления имитацией сети.

Решение задачи коммивояжера на основе сети Петри

Задача коммивояжера – одна из самых известных задач комбинаторной оптимизации, заключающаяся в отыскании самого выгодного маршрута, проходящего через указанные города по одному разу с последующим возвратом в исходный город [4]. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз – в таком случае выбор осуществляется среди гамильтоновых циклов.

Общая постановка задачи и большинство её частных случаев относятся к классу NP-сложных задач. Поэтому алгоритмы решения этой задачи делятся на точные и приближенные. Все точные алгоритмы фактически представляют собой оптимизированный полный перебор вариантов. В некоторых случаях эти алгоритмы достаточно быстро находят решения, но в общем случае приходится перебирать все n! циклов.

Рассмотрим метод решения задачи коммивояжера методом случайного поиска с применением сети Петри с памятью состояний. Данный метод не гарантирует оптимального решения, но может обеспечить приемлемое решение за минимальное время. Поскольку постановка задачи не допускает повторного попадания коммивояжера в один город, то для исключения такой возможности можно применить вектор статической маркировки. Элементы данного вектора будут определять количество посещений города за время имитации. Соответственно, маркер может попасть в позицию, только если соответствующий элемент вектора статической маркировки меньше единицы. Формально указанное условие может быть представлено в виде модифицированного условия срабатывания сети:

ц [ k ] + D ■ u [ k ] > 0 z [ k ] + D ■ u [ k ] < 1

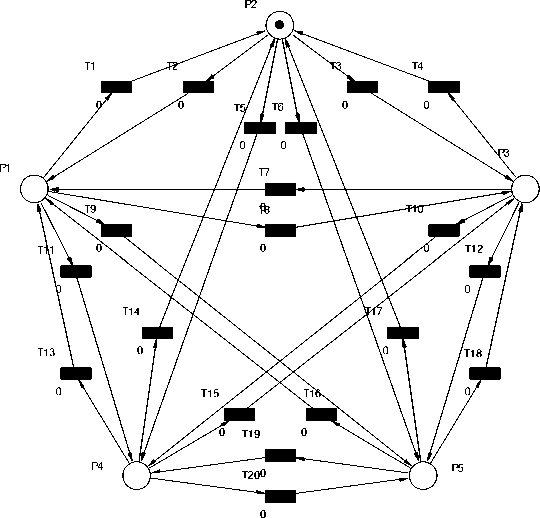
Определив формальные условия (2) и правила (1) изменения состояния сети, можно переходить к формированию её структуры. В структуре сетевой модели города представляются позициями, каждая из которых связана с любой другой позицией через два перехода. Один из переходов моделирует входящий путь в город, другой – исходящий. На рис. 2 приведен пример модели для пяти городов, построенной по описанным принципам. Принципы формирования – 525 – сетевой модели сохраняются для разного количества городов n. Далее проводятся эксперименты для n = 12.

Процесс решения задачи коммивояжера организуется как процесс прямой имитации сети до тупикового состояния. Для оценки общего времени маршрута используется временная сеть Петри, моделирующая задержки на переходах [5]. Далее, определив желаемое время, выполняется серия экспериментов с сетевой моделью с определением фактического времени маршру-тав каждой реализации.

Эмпирически была проверена применимость сети Петри с памятью состояний для решения задачи коммивояжера при разном количестве городов ( n = 4,…,50) экспериментами в программной системе MathCAD [6]. Результаты вычислений для одного из вариантов маршрута приведены на рис. 3.

В матрице на рис. 3 колонки соответствуют маркировкам сетевой модели, а строки – последовательным номерам посещаемого города. В последней строке приведены значения времени маршрута на каждом шаге. Матрица иллюстрирует работоспособность предложенного метода, так как по выделенному маршруту видно, что каждый город посещается один раз. Оптимальность маршрута оценивается по последнему значению времени.

Применение имитационной модели на основе сети Петри имеет следующие плюсы:

• 1.    Возможность применения сетевой модели как для поиска оптимального маршрута, так и для реализации маршрута, т.е. управления объектом в реальном времени.

• 2.    Простота изменения механизма выбора переходов в маршрут. Например, можно реализовать так называемый жадный алгоритм, выбрав в качестве приоритетного правила при имитации правило наименее длительной операции.

  

m(t) =

	1	2	3	4	5	6	7	8	9	10	11	12
1	1	0	0	0	0	0	0	0	0	0	0	0
2	\	0	0	1	0	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	0	0	0	0
4	0	1		0	0	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0	0	0	0	1	0
6	0	0	0	0	0	1	0	0	0	0	0	0
7	0	0	0	0	0	0	0	1	0	0		0
8	0	0	0	0	0	0	0	0	1		0	0
9	0	0	0	0		0	0	0	0	1	0	0
10	0	0	0	0	1	0		0	0	0	0	0
11	0	0	0	0	0	0	1	0	0	0	0	0
12	0	0	0	0	0	0	0	0	0	0		1
13	0	1	2	6	9	16	25	29	33	34	40	42

Рис. 3. Результаты сетевого моделирования

В качестве итога можно отметить, что автор не ставил цели найти наилучший метод решения задачи коммивояжера, а только планировал показать на конкретном примере применимость сетей Петри с памятью состояний для решения конкретных задач. С точки зрения качества получаемых решений существуют более рациональные методы решения, например муравьиный алгоритм или нейронные сети. В этой связи вопросы сравнительного анализа методов не рассматривались.

Заключение

Сформулированные в статье принципы организации памяти состояний сетей Петри, не изменяя фундаментальных принципов их функционирования, формируют дополнительные возможности для моделирования реальных объектов и процессов. Память состояний сети позволяет формировать более сложные алгоритмы имитационного моделирования, чем традиционные для сетей Петри.

Предметом дальнейших исследований по тематике статьи являются вопросы использования статической маркировки для решения отдельных задач управления.