Сгущение учебной профессионально ориентированной информации по математике при обучении студентов-экономистов

Перед высшим профессиональным образованием стоит задача подготовки профессионалов высокого международного уровня, такой подготовке должно способствовать эффективное формирование и развитие профессиональных компетенций еще на этапе обучения в вузе [1].

У студентов, обучающихся по экономическим направлениям, определенные трудности получения образования связаны с большим объемом информации, которую они получают с первых дней занятий по математическим дисциплинам; со сложностью восприятия теоретических вопросов при решении прикладных задач; с отсутствием навыков системно и напряженно работать, усваивать материал на нужном уровне.

Возникает необходимость специальным образом решить проблему интенсификации изучения математических дисциплин, что приводит к идее использования технологического подхода, в который включают техники сгущения (уплотнения, сжатия) учебной информации путем дополнительной систематизации и обобщения.

Процесс графического сгущения учебных знаний, по мнению авторов пособия «Графическое сгущение учебной информации» [2, с. 5], состоит из трех этапов-уровней: кодирования знаний, укрупнения (ранее закодированного), структурирования (ранее укрупненного).

На первом этапе происходит осмысление содержания преподаваемого материала: выявляются основные дидактические единицы, а затем учебный материал кодируется. Под кодированием учебной информации понимают процесс сокращенной записи отдельных понятий, определений, фактов, явлений, величин и т.д. при помощи определенных знаковых, рисуночных или цветовых кодов.

Под укрупнением закодированного материала понимают нахождение общих и различных черт, выделение взаимосвязей (логических, ассоциативных, формальных и т.п.) между ними, сплочение информации в единое целое в виде мнемонических или логических средств укрупнения. Материал, организованный каким-либо способом (визуально, семантически или путем классификации), запоминается и воспроизводится гораздо легче, чем неорганизованный материал.

Под структурированием укрупненного материала понимают создание крупноблочных графических опор, таких как блок-схемы, граф-схемы, логико-смысловые модели. Учебному материалу придается целостная форма, которая позволяет с наибольшим эффектом усваивать данную информацию.

Одним из дидактических способов уплотнения мысли является создание крупноблочнографической наглядности. Графические изображения укрупненного блока учебной информации (опорного конспекта) имеют различные названия: системные опорные конспекты (Т.В. Лаврентьева), синтетические конспекты (В.Ф. Шаталов, С.Д. Шевченко), блок-схемы (О.Е. Лисейчиков, М.А. Чошанов), граф-схемы, матрицы (П.М. Эрдниев), концепты (М.П. Щетинин), фреймы (Р.В. Гурина, Т.Н. Колодочка), логико-смысловые модели (В.Э. Штейнберг), семантические сети и т.д.

В опорных конспектах содержание концентрируется в ключевых словах и формулах, условных обозначениях и сокращениях. Смысл опорного конспекта как средства обучения состоит в том, что он через зрительно воспринимаемые образы, знаки и другие изобразительные средства вызывает из памяти студентов необходимые ассоциации, опорные знания, помогает достаточно компактно выстроить систему некоторого блока содержания, облегчает понимание его структуры и тем самым способствует усвоению. Ведь чем больше опор, тем упорядочение материал, что значительно облегчает усвоение нового знания.

В нашем исследовании использован технологический подход, развитию которого способствуют техники работы с опорными конспектами, опорными схемами, с граф-схемами, мнемоническими схемами, что включает различные каналы восприятия обучаемого. Систематизация учебного материала в виде связанных между собой схем, таблиц, рисунков позволяет выявить его структуру, предложить наглядный иллюстративный образ.

Приведем пример одной из разработанных таблично-матричных опор [3, с. 24] для обучения студентов по экономическим направлениям под названием «Основные формулы дифференциального исчисления» (рис.1), включающей схематизированную профессионально значимую информацию, позволяющую достаточно быстро, решать прикладные задачи по указанной теме.

Схемы, исходя из их назначения в образовательном процессе, могут выполнять следующие функции: обучающую, контролирующую, диагностическую, корригирующую, гностическую [4].

Учитывая многофункциональность схем, их можно условно разделить на:

• -    схемы-опоры в виде учебных карт, формул, инструкций, облегчающие усвоение словесно излагаемого материала;

• -    граф-схемы, упорядочивающие связи между отдельными элементами, облегчающие логическую классификацию изучаемого материала;

• -    схемы распознавания, используемые обычно в технических науках;

• -    блок-схемы, являющиеся средством моделирования и анализа деятельности.

В отличие от обычных графически выполненных схематических рисунков, широко используемых в обучении, граф-схемы представляют собой качественно новое средство, позволяющее определить поток словесных рассуждений в виде логических отношений и связей между его отдельными элементами. Граф-схему можно охватить одновременно («единым взором») в отличие от словесного текста, который воспринимается только при последовательном чтении.

Граф-схемы способствуют освобождению от второстепенных сведений, нерационального расположения теоретического материала, исключают разрозненность учебного материала, обеспечивают обобщение и систематизацию, устраняют перегрузки, экономят учебное время.

Использование графических схем позволяет студентам выявлять логические отношения и взаимосвязи между этапами рассуждений, учит планировать свою деятельность, развивает наблюдательность и самостоятельность.

Граф-схема подключает неиспользованные резервы мышления, а именно - создает символический и словесный образы в пределах одного восприятия, что означает двустороннюю перекодировку информации между правополушарными и левополушарными механизмами памяти и мышления. В большинстве видов человеческой деятельности преобладает функционирование или левого, или правого полушария мозга. Математика и методики ее преподавания является исключением из этого правила [5, с. 63]. Процесс обучения математическим дисциплинам должен строиться с учетом индивидуально-психологических особенностей личности, что необходимо для более глубокого усвоения изучаемого материала.

В обучении студентов по экономическим направлениям мы используем граф-схемы по различным темам математических дисциплин. Это актуально как при объяснении нового материала, так и при обобщении знаний по дисциплине, федеральном итоговом тестировании. Например, граф-схема по теме «Случайная величина» (рис. 2), включающая большой объем информации по видам случайных величин, их числовых характеристик и распределений. Для эффективного использования схем обучающиеся должны владеть навыкам анализа, синтеза, сравнения.

В процессе обучения студентам необходимо давать возможность изобретать самим и использовать уже готовые для запоминания, сохранения и воспроизведения информации, различные приемы или мнемотехнические средства. Они должны включать различные способы умственной обработки учебной информации, ее схематического, графического и символьного представления. Навыки графического конспектирования способствуют формированию умения самостоятельно работать с источниками знаний, развитию памяти, логического мышления студентов.

Основные формулы дифференциального исчисления

>х о т ч о m to s о CL С к St т ш X о с X О. с	Геометрические
	Угловой коэффициент касательной к графику функции в точке Ко					k™ =f,(x0) = tgc(
	Уравнении екасательной к кривой в точке Хо					y-f0} = f'(xg)(x-x0)
	Уравнение нормали					У f(x0)   ,,, Jx x0) f (x0)
	Угол между двумя кривыми					-   l+f^Xg) f^(xe)
	Механические
	Скорость				V = s'(t)
	Ускорение				a = V(t) = s'(t)
	Сила тока				i=Q'(t)
	Плотность стержня				p = m'(x)
	В математическом анализе
	6 ф	Экстремумы и интервалы монотонности функции		a) f '(х о ) = 0, f(х0 ) - мякшмум ^^~~^^ -Г (Х)
				6)f'(xo) = OT    f(x0) —минимум ^-^-у^^— _ f'(х)
				в) f'(Хо) # 0, в х. нет экстремума ~^—~~^^ - f <х) Т~^^* - f <х)
		Наибольшее и наименьшее значения на отрезке		1) f (Кд ) = 0 или не существует. х о Е [а;Ъ] 2)f(a) = ,f(x0) = _f(b) = .. 3) выбрать
		Точки перегиба и интервалы выпуклости функции		f "(xg) = 0        Хц - точка перегиба ~ ^^^^ "^ CO ^^^^^^ f ' (x)
				f "(x q ) ^ 0      в Xj нет перегиба ^ ^^^ Г (X) ^^Y^^ T w
	ПравилоЛопиталя			f(x)        f'(x) Lim----= Lun---- x->xo g(x) x-»xo g’(x)
	fl -1		Ряд Тейлора Ряд Маклорена	f(x) = f(x0) + Г(х0) ■ (x - x0) + -^(x-X^-..+ _^(Х_Х1).^^ n! При X(=0
			Дифференциал	f(x + Ax) = f(x) + f'(x)Ax

•K О I 4 о co го s о О. C LU s Ш о s Л co	Формулы дифференцирования
	1. с'= 0 (с = const), u' = 1,     (1cu')'= с • и'
	iW = nu"Vu'
	3. (aB)'=aulna u'      (e™)		= eu ■ u'
	4- Й x u' J n         (lnu) = — (log, и I =------la > 0,a * 11     ■    7n ulna
	5- (sin и ) = cos z/ ■ u'	6. (cosuj		= —sinuu'
	/ V u' 7- (tgu) -    2 cos" 11	8. (ctgu(		_ u' sin2 и
	, /    - V u	10. laivco
				"     7i-u2
	11. (arete u) =—-— т "      l + uz	/        у      u' 12. larcctg u I =--T- 1-u2
	Правила дифс	)еренцирования
	с'=0(c = const), u' = l, (ai)' = cu'
	(u ± v)' = u' ± v' (iw)r = u' ■ V 4- U ■ v'		1 u>	u'v - uv' V2

Экономические	приложения
Предельные издержки производства	МС - c'(q)
Предельный спрос (предложение)	|D'(p)|.    (S'(p))
Предельная полезность	MU= U'(q)
Предельная склонность к потреблению Предельная склонность к сбережению	MPC = C'(Y). C'CY) +S'(Y)=1. MPS=S'(Y)
Предельная производительность труда Предельная фондоотдача Темп изменения выпуска	Ца+1)х f(a)+fr(a). Yl =paK“LH, y^aaK""1!?. ^L- Уи.’Тк— Ущ^
“Золотое правило" экономики:	f(a)>^ P
Ставка банковского процента	r = (fiiK)'
Эластичность спроса (предложения) на товар по цене	EP(n) = ^n; (Ep(s)=|s;)
Распределение налогового бремени между потребителем и производителем	Др     Ep(S) t-Др   Ep(D)
Минимизация издержек склада за единицу времени	Gmin = Q= / 2KM \l h
Максимизация прибыли	P^= F'(x)=^ V

Рис.1 - Таблично-матричная опора

В некоторых случаях можно предлагать обучающимся заполнить пустые клетки схемы, например, мнемоническая блок-схема «Слепая схема» (рис. 3). Целью использования мнемонических схем в обучении является способность к легкому запоминанию основных элементов знаний изучаемой темы. К мнемоническим средствам запоминания относятся: аналогии, ассоциации, расположения на уровне памяти.

НЕПРЕРЫВНАЯ P(A)=F(X)

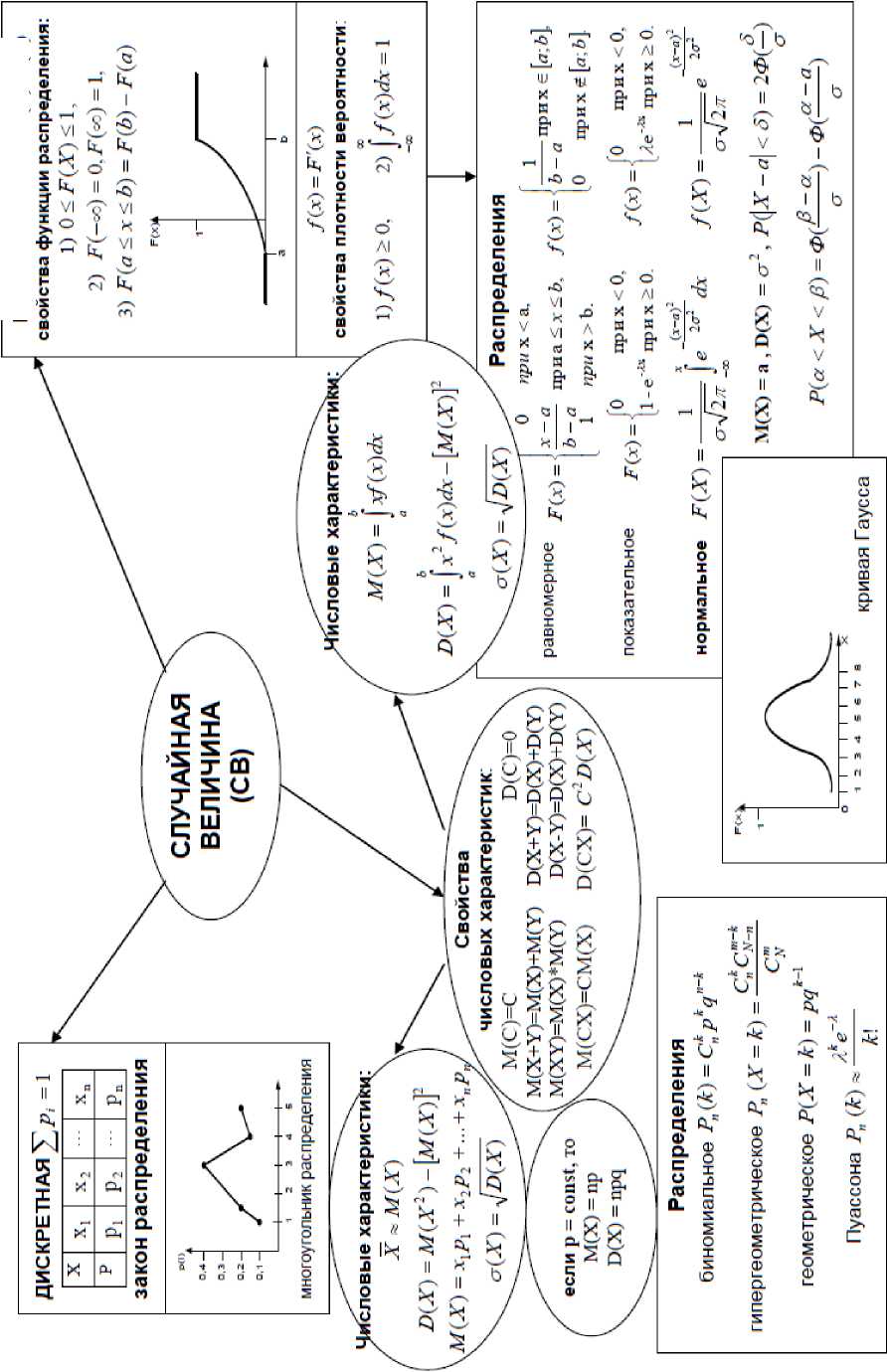
Рис. 2 - Граф-схема

«Слепая схема» по теме «Исследование функции»

Заполните схему, учитывая последовательность действий при исследовании функции, проанализировав и разбив их на части. Приводим эти действия в случайном порядке.

Необходимое условие экстремума Поведение функции вблизи точек разрыва

Построение графика функции Интервалы выпуклости функции Наклонные асимптоты

Интервалы знакопостоянства функции Значения функции в точках перегиба

Экстремум функции

Необходимое условие перегиба

Достаточное условие экстремума

Вертикальные асимптоты

Область определения функции

Четность, периодичность

Интервалы возрастания, убывания функции

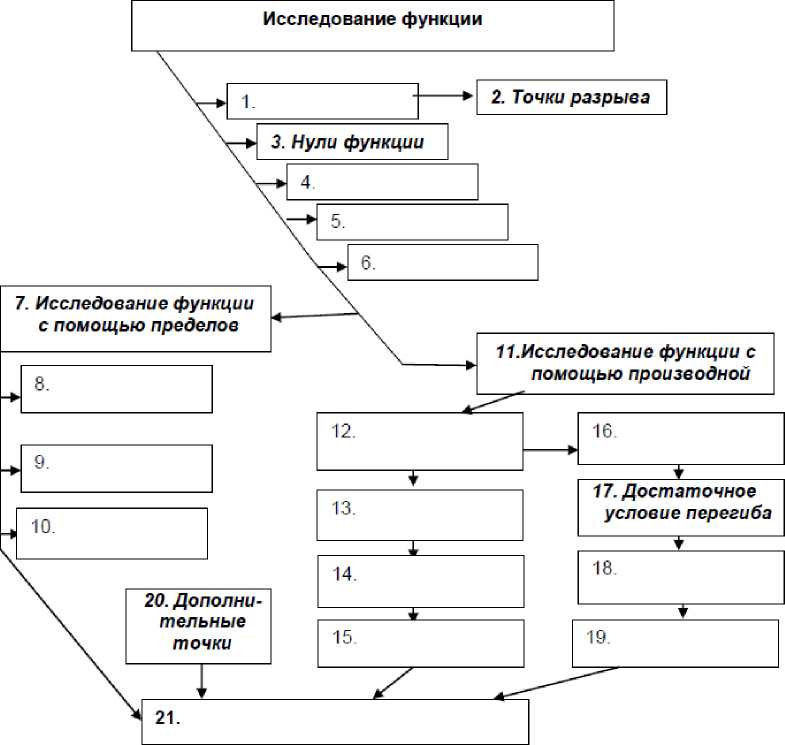
Рис. 3 - Блок-схема

При составлении опорных конспектов, по мнению В.Ф. Шаталова [6], и опорных схем необходимо учитывать следующие основные требования к изображаемой информации: лаконичность (краткость и четкость изложения); емкость (краткость и содержательность изложения); ассоциативность (установление сходства и различия между представлениями), структурность (стройность, связность крупных блоков); смысловой акцент (оригинальное расположение символов; отделение одного блока от другого при помощи специальных фигур, обводок и т.д.; цветовое решение); понятность, доступность воспроизведения.

В хорошей символической схеме учебный материал «упакован» так, что в устном его озвучивании можно многократно варьировать отдельными частями схемы. Вариативное синонимическое повторение позволяет раскрыть учебный материал с разных сторон, держа в памя- ти всю его целостность и внутреннюю стройность. При этом должны быть как вербально, так и визуально выделены главные и вспомогательные информационные единицы схемы.

Следует учитывать, что при сгущении учебного материала прочность усвоения достигается при подаче учебной информации одновременно на четырех кодах [7, с. 78]: рисуночном, числовом, символическом и словесном, что способствует развитию определенных профессиональных компетенций будущего экономиста.

Таким образом, можно сделать следующие выводы:

Более высокой результативности в обучении студентов по экономическим направлениям можно достичь при условии использования профессионально ориентированного дидактического обеспечения курса математики, проектируемого с использованием современных образовательных технологий.

Профессионально ориентированная модель, основанная на технологическом подходе, повышает мотивацию к изучению предмета, активизирует познавательную деятельность студентов, что способствует формированию и развитию профессиональных компетенций будущего экономиста.

Ссылки:

• 1.    Грушевский С.П., Шмалько С.П. Формирование профессионально-значимых качеств личности студентов экономических направлений в процессе математической подготовки // Теория и практика общественного развития. 2011. № 3. С. 157-162.

• 2.    Грушевский С.П., Гузенко В.В., Карелина З.Г., Касатиков А.А., Остапенко А.А., Прохорова Н.Г., Шубин С.И. Графическое сгущение учебной информации / под научн. рук. и ред. Остапенко А.А. Краснодар, 2005.

• 3.    Боровик О.Г., Грушевский С.П., Засядко О.В., Карманова А.В., Шмалько С.П. Приложения в экономике функции, производной и интеграла: учебное пособие. Краснодар, 2010.

• 4.    Шушарина Н.П. Программа элективного курса «Способы свертывания информации, или Как научиться    правильно    списывать».    URL:

• 5.    Карпова В.B. Прикладная направленность преподавания математики в военно-инженерном вузе как средство формирования системности научных взглядов курсантов: дис.... канд. пед. наук. Пермь, 1999.

• 6.    Шаталов В.Ф. и др. Опорные конспекты по кинематике и динамике: кн. для учителя: Из опыта работы М., 1989.

• 7.    Эрдниев П.М. Системность знаний и укрупнение дидактической единицы // Сов. педагогика. 1975. № 4. С. 72-80.