Shear angle effect on the engineering constants of woven fabrics

In application and usage, the angle between weft and warp, described as the shear angle, changes dues to the dynamic forces of tension and pure shear. This tends to have a significant impact on the behaviour and response of the fabric in usage. It is paramount to determine how this constant change in angle affect the geometry of the fabric and how it affects the textile formed from this fabric. Fabric properties including weave type and setting have significant effects on the shear response of fabrics [1]. A number of experimental methods proposed fpr measuring shear deformation in woven fabrics include the picture frame test method (PFTM), the Kawabata evaluation system for fabrics (KEF) and the bias-extension test method (BETM). Most other research works have delved into experimental investigation of the shear angle, displacement, tensile and shear forces of the fabric. There is a relationship between wrinkling and shear angle.

The study showed how the critical shear angle called locking angle has a high dependence on such parameters as yarn spacing, tow size and friction [2]. In both applications as textiles in clothing and reinforcements in composites, wrinkling and drapeability play a big role in terms of shear angle, although the latter carry more load. The pin-join model is famous in determining the deformation of woven fabrics based on kinetic-geometric analysis [3]. The main assumption is that yarns, inextensible and incompressible, are pinned at points of intersection and are free to relocation spatially but not translate in real time.

A number of research works have studied the effect of shear angle caused by different factors on textile in use. The pin-join model is one of the prominent models developed for predicting the warp-weft interaction in dynamics. One such work involves fixing the clamp holding the fabric on one end and applying a shearing force at the other end by moving the clamp at a constant spend [4, 5].

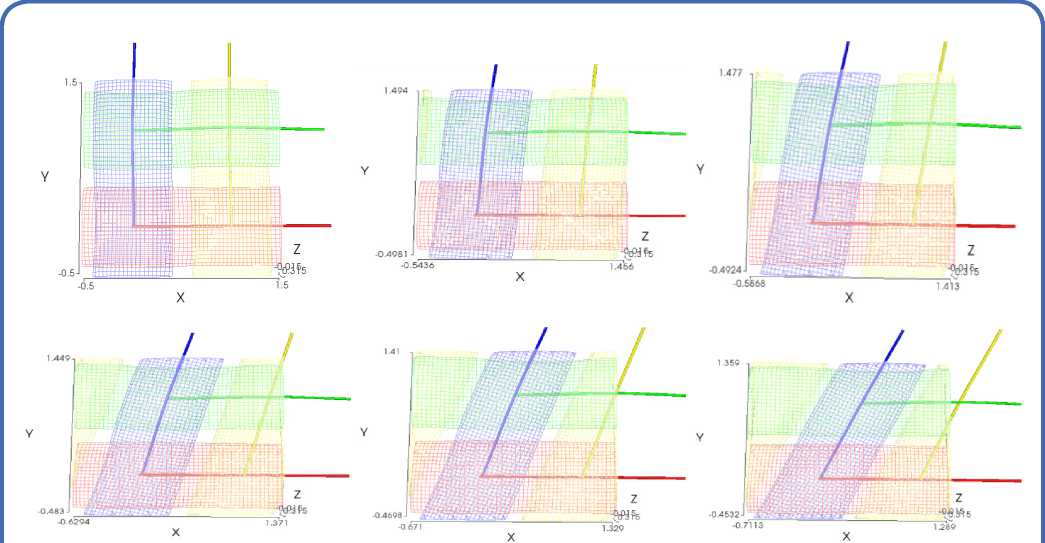
Figure 1 – Shear Angle [From Left to right (0–25o:5o)]

Another practical method, as given by numerous authors, is the picture frame method where the fabric sample is inserted in a frame. A measured tensile load is exerted along the corners of the frame – several configurations are used depending on the fabric shape and size, chosen test speed, frame design etc [6–12]. The proposed method of investigating the effect of shear angle on fabrics will be used in further works where the model is exported to commercial software, relevant boundary conditions are imposed and the system is solved in the fashion of the live experimental method.

This work will investigate the effect of shear angle on a 2x2 plain-woven fabric. The model is composed of lenticular-cross section yarns generated from TexGen. As in Table 2, the geometrics of the yarn are given as 1.0 mm for the yarn spacing, 0.8mm for the yarn width, and 0.3 mm for the fabric thickness and 0.1mm for the yarn height. It is also technically desirable to rework the process in Ansys 2022 R2, where the shear angle is initially zero and then parametrically ramped to 30o. Finally, the effect of the geometric property of the model is investigated as well by parameterizing, for instance, the yarn spacing, yarn width and fabric thickness which are known to affect both the in-plane and transverse properties of the RVE in general.

SETTING UP THE MODEL

The model is a conventional plain-woven 2x2 fabric generated in-situ using the in-built Material Modeller module in Ansys 2022. Standard periodic boundary conditions are built into the system so that opposing sides of the model are kinematically tied to a corresponding side using simple canonical equations. The proposed geometrical model is automatically generated in the software. The material properties are given as follows:

The yarn type greatly influences the behaviour of the fabric. In this case, the flattened lenticular (high fibre volume fraction) yarn type was chosen. To retain full orthotropic behaviour of the fabric, the fabric is set not to align with the x-direction. Setting this option will form a 4-yarn arrangement where each pair of yarns lay in opposite positions and form a close square. The periodicity condition is activated and to allow for solutions for the six load cases, the symmetry in XY, XZ or YZ is not turned on.

YARN AND FABRIC GEOMETRICS

The yarn geometry plays a vital role in the shear angle which is directly related to the fibre angle. Specifically, in the bias-extension experiment, the shear angle, Ѳ_L , is calculated as:

0 = - - 2 0 = ^П - 2cos ^{- 1} f L 0 +^- ^ , (1)

L 2 2 I L0^2 )

Ѳ_L is the angle between the warp and weft whereas L ₀ is the difference between the original test length L and width W , such that L ₀ = L – W , and δ is the displacement of the sample during the bias-extension test.

RESULTS AND DISCUSSION

Since the model was not solved with symmetry in XY, XZ or YZ, all six load cases are accounted for. The plots are a comparison of Young’s modulus, Shear modulus and Poisson’s ratio. The different cases of shear angle are observed. A keen observance is made of how sensitive each of the engineering constants are to the shear angles which ranged from zero through 20^o with a 5^o step. The effect of change in shear angle is the most significant in E ₁ , less in E ₂ and the least in E ₃ . The shear angle also affects the possible values the software is able to compute.

Table 1 – Material Properties
E (GPa)	ν	B (GPa)	S (GPa)	ρ (g/cm3)
73	0.22	43.45	29.918	2.56

Table 2 – Model Geometry
Yarn Spacing	Yarn Width	Fabric Thickness	Yarn Height
(mm)
я       1.00	0.80	0.30	0.10

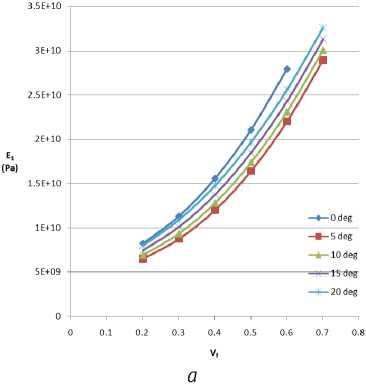
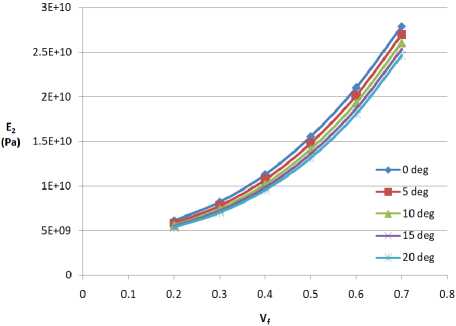
Figure 3 – (a) E1 vs Vf (b) E2 vs Vf

b

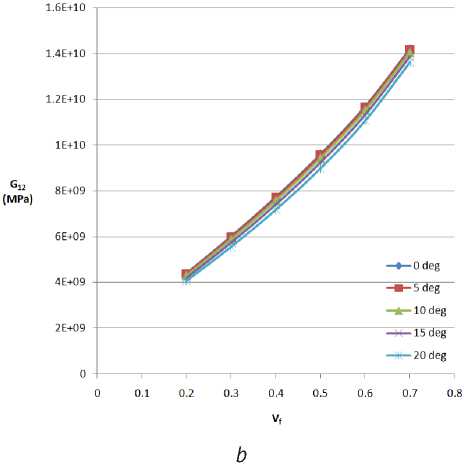
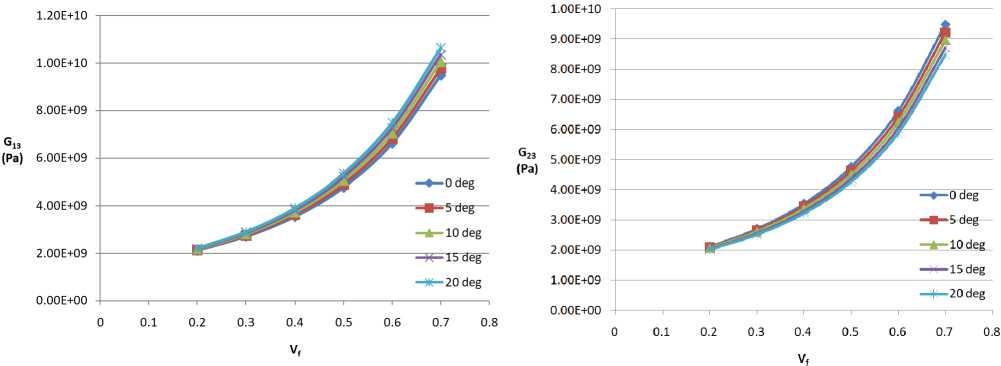
Figure 3b, 4a and 4b are the plots showing the relationships with shear modulus ( G ), and how change in shear angle affects its relation with the fibre volume fraction. G ₁₂ , G ₁₃ and G ₂₃ all showed very insignificant dependence on the shear angle.

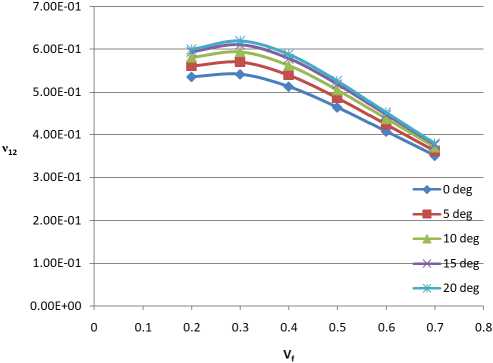
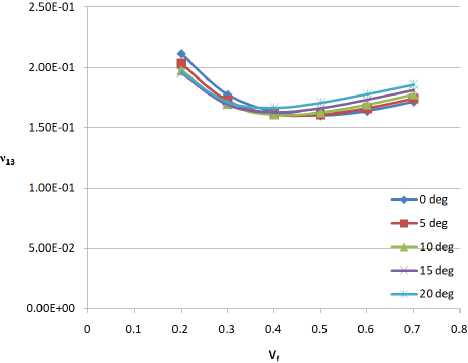
From figure 5a, 5b and 5c, the shear angle showed the most significance and effect. ν12 and ν23 showed more variation with the shear angle than ν13. Generally, this can be explained in the fact that shear modulus has a direct correlation with Poisson’s ratio.

ACKNOWLEDGEMENT

This publication was written at the Technical University of Liberec as part of the project "Research of advanced materials, and application of machine learning in the area of control and modeling of mechanical systems"

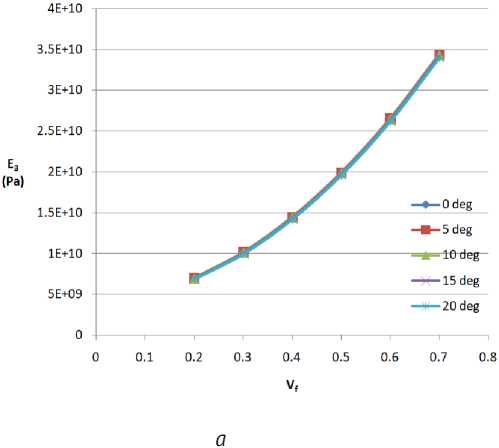
Figure 3 – (a) E3 vs Vf (b) G12 vs Vf

аb

Figure 4 – (a) G13 vs Vf (b) G23 vs Vf

nr. SGS-2022-5072 with the support of the Specific University Research Grant, as provided by the Ministry of Education, Youth and Sports of the Czech Republic in the year 2023.

а

Figure 5 – (a) ν ₁₂ vs V_f (b) ν ₁₃ vs V_f

b

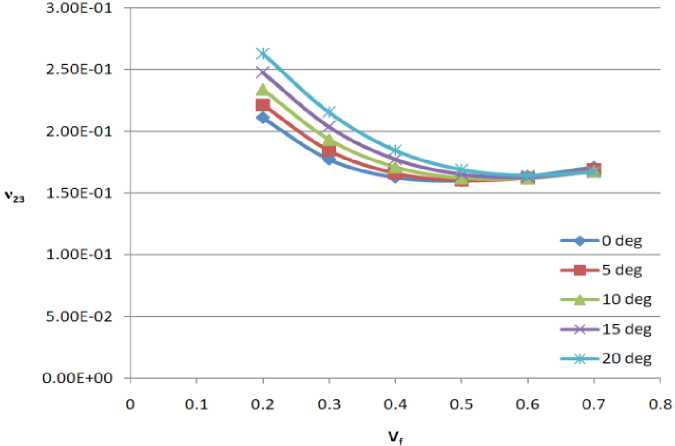
Figure 6 – ν ₂₃ vs V_f