Схемы нагружения при моделировании процесса взаимодействия внешнего движителя геохода приконтурным массивом пород

Для исследования влияния геометрических параметров внешнего движителя (ВД) геохода и винтового канала на НДС породы [1 - 4] необходимо провести математическое моделирование процесса взаимодействия ВД с геосредой [3, 4], что в свою очередь позволит провести теоретические исследования в этом направлении.

Для получения картины НДС породы приконтурного массива при взаимодействии ВД с геосредой необходимо решение сложной контактной задачи. Такие задачи успешно решаются численными методами моделирования с использованием МКЭ [5 — 7].

Для создания численной модели взаимодействия ВД геохода с геосредой необходимо сформировать исходные данные, в число которых входят: физикомеханические свойства геосреды, геометрические параметры внешнего движителя, винтового законтурного канала и их со- пряжения, силы взаимодействия, схема и способ приложения сил к модели и др. [9-10].

Физико-механические свойства геосреды являются известными табличными данными [11].

Геометрические параметры лопасти и канала описаны в работе [12, 13] и являются изменяемыми параметрами, обоснование которых и есть цель моделирования.

Для определения сил взаимодействия необходимо создание модели взаимодействия систем геохода с геосредой и между собой. Задача определения сил, возникающих при движении, может быть решена аналитически.

Взаимодействие лопасти с геосредой может осуществляться при разных моделях поведения геосреды.

При движении по сыпучим или вязко-подвижным породам (рис. 1) геосреда воздействует как на свободную (перед- нюю), так и на опорную (заднюю) поверхность лопасти ВД [14-19]. При этом происходит «проскальзывание», лопасть опорной поверхностью надвигается на геосреду, со стороны свободной поверхности лопасти формируется «пустота». Это приводит к «перетеканию» геосреды через лопасть. Разность давлений на опорной и свободной поверхностях формирует тяговое усилие, создаваемое движителем. При такой модели взаимодействия отсутствует жесткая кинематическая связь между уг- лом поворота движителя и перемещением геохода.

Подвижность геосреды обеспечивает взаимодействие по всей опорной поверхности лопасти. Поэтому увеличение площади лопасти однозначно приведет к увеличению максимального развиваемого тягового усилия. При этом значение имеет как длина, так и высота лопасти движителя.

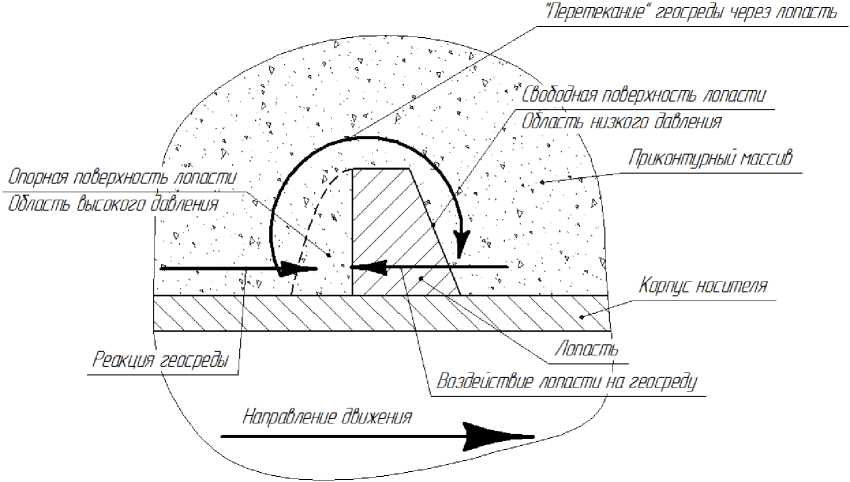
Рис. 1. Взаимодействие ВД с подвижной средой

При движении по достаточно крепким породам (рис. 2) взаимодействие происходит по опорной поверхности лопасти, а свободная поверхность может не соприкасаться с породой.

Ограниченные податливости лопасти и геосреды, отклонения размеров, формы и расположения обусловливает «точечный» характер взаимодействия лопасти с геосредой, или взаимодействие по пятну контакта ограниченных размеров. В этом случае максимальное развиваемое усилие зависит не от площади лопасти, а ограничивается несущими способностями либо межвит-кового целика, либо лопасти ВД. При этом длина и высота лопасти оказывают неоднозначное влияние на максимальное развиваемое тяговое усилие.

Очевидно, что при движении по слабым и крепким породам необходимы совершенно различные подходы к расчету и проектированию внешнего движителя геохода.

Рассмотрим взаимодействие ВД с крепкими породами, т.е. с выполнением следующих условий:

• •    жесткая кинематическая связь между углом поворота движителя и подачей агрегата на забой;

• •    неразрушение межвиткового целика.

  

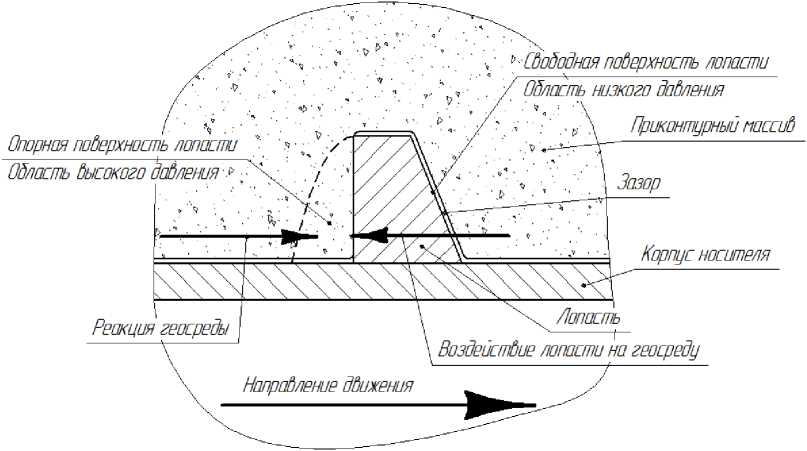
  Рис. 2. Взаимодействие ВД с крепкой средой

  
  
  

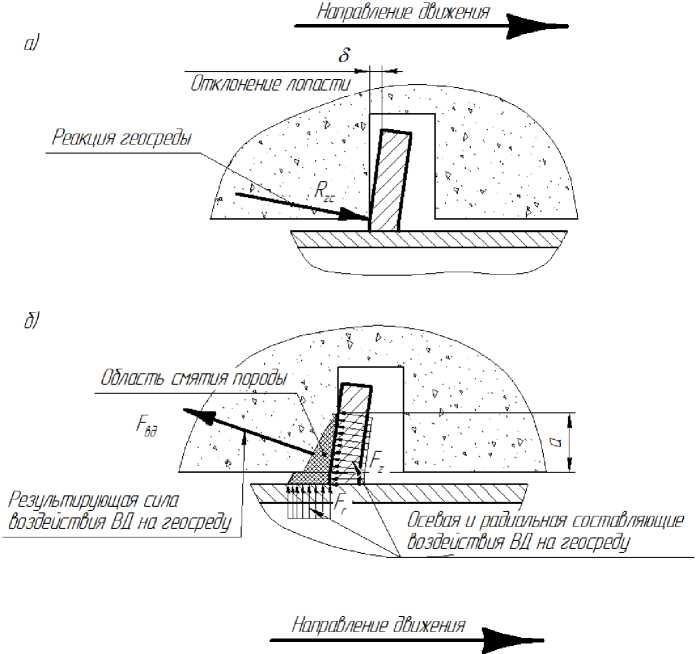
  Рис. 3. Схема взаимодействия ВД с геосредой:

  а - деформация лопасти ВД под воздействием реакции геосреды, б - формирование пятна контакта и сил взаимодействия ВД и геосреды

  
  

На рис. 3 показана схема силового взаимодействия лопасти и геосреды при условии совпадения ненагруженных профилей опорных поверхностей лопасти ВД и винтового законтурного канала.

Из схемы на рис. 3 видно, что к лопасти нагрузка прикладывается в области её подножья, а к породе в области наружной рабочей кромки канала. Очевидно, что до наступления процесса смятия породы (рис. 3, а) площадь кон- такта стремится к нулю. Это приведет к превышению предела прочности породы и к формированию области смятия породы (рис. 3, б). Граница области смятия является границей разрушения, поэтому сделаем допущение, что на границе области смятия породы напряжения в породе равны или весьма близки к пределу прочности на одноосное сжатие и направлены по нормали к границе области смятия породы. Также сделаем допущение, что модель поведе- ния породы в области смятия близка к поведению вязкой среды.

Поверхность, ограничивающую область смятия с одной стороны и неразрушенную породу с другой, можно рассматривать, как вновь сформированную опорную поверхность законтурного канала, к которой приложена равномерно распределенная нормальная нагрузка, численно равная пределу прочности породы на одноосное сжатие (рис. 4).

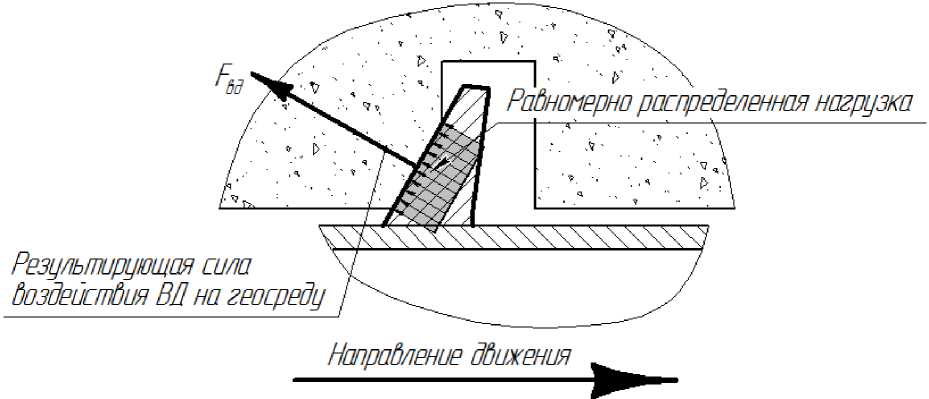
Рис. 4. Схема взаимодействия ВД с геосредой

На рис. 5 показана схема варианта силового взаимодействия лопасти и геосреды при условии несовпадения нена-груженных профилей опорных поверхностей лопасти ВД и винтового законтурного канала. Из схемы на рисунке видно, что сначала нагрузка прикладывается к вершине лопасти и в области внутренней рабочей кромки канала (рис. 5, а). После приложения нагрузки профиль лопасти деформируется, и опорные поверхности совпадают (рис. 5, б), а закон распределения на- грузки по пятну контакта определяется геометрическими и механическими характеристиками лопасти. При такой схеме взаимодействия можно избежать или минимизировать формирование области смятия породы.

Схемы распределения нагрузки по пятну контакта, приведенные на рис. 4 и 5, позволяют допустить применение равномерно распределенной нагрузки при моделировании процесса взаимодействия лопасти ВД с геосредой.

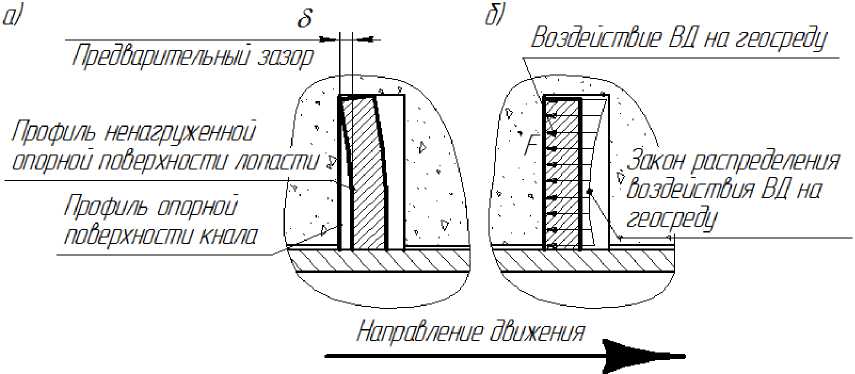
Рис. 5. Схема взаимодействия ВД с геосредой: положение профилей опорных поверхностей а - до приложения нагрузки, б - после приложения нагрузки

Выводы:

• •    при взаимодействии ВД с геосредой происходит деформация лопасти, причем податливость лопасти определяет характер взаимодействия;

• •    при совпадении профилей опорных поверхностей ненагруженных лопасти и винтового законтурного канала формируется область смятия породы;

• •    на границе области смятия породы имеет место равномерно распределенная по поверхности нагрузка, равная переделу прочности породы на одноосное сжатие;

• •    учет упругой деформации при определении геометрических параметров лопасти и законтурного канала позволит избежать или минимизировать процесс формирования области смятия в пятне контакта;

• •    при моделировании процесса взаимодействия ВД с геосредой возможно применение равномерно распределенной нагрузки;

• •    при моделировании процесса взаимодействия ВД с геосредой возможно применение произвольного закона распределения нагрузки.