Схемы расширения понятия числа

Основным понятием в математике является число. Одна из содержательно – методических линий в школьном курсе математики является линия числа. С 1 по 11 класс происходит изучение чисел.

На началах человеческой цивилизации в качестве обыкновенных потребностей деятельности людей произошло возникновение числа. Учение о числе основывается на арифметике натуральных чисел.

Развитие числовой линии состоит в последовательном расширении множества натуральных чисел по следующей схеме, которую называют логической N^Z^Q^R^C. (Рис. 1)

Рисунок 1

Помимо логической схемы расширения понятия числа существует историческая схема. В исторической схеме дроби появились намного раньше отрицательных чисел, в этом и есть различия между двумя схемами. В школьном курсе устоялась историческая последовательность расширения числа. (Рис.2)

Историческая схема N0cQ+cQcRcC уступает логической в стройности, но заслуживает предпочтения из дидактических соображений.

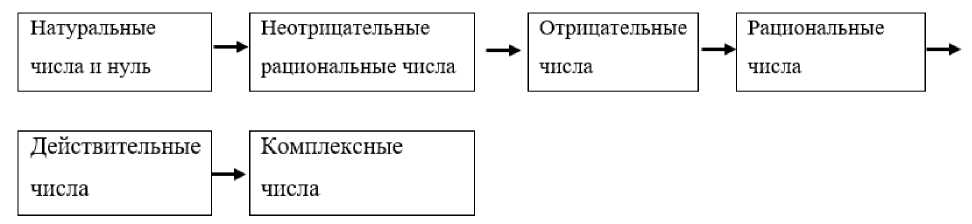
Рисунок 2

Школьная схема расширения числа даёт обоснование того, что положительная дробь более понятней детям, нежели отрицательное число.

В 1968 году была реализация логической схемы развития понятия числа в школьном курсе по математике. В 4 классе были проведены эксперименты по расширению множества натуральных чисел до множества целых чисел, но в 1970 г принятая программа, возвратилась к исторической схеме. Она предусматривала лишь изучение арифметики десятичных дробей раньше арифметики обыкновенных дробей.

Натуральные числа и нуль, обыкновенные дроби, десятичные дроби, положительные и отрицательные числа и в заключение в виде обобщения целые и рациональные числа – последовательность расширения понятия числа в 5-6 классах по программе 1996 г. Изучение иррациональных чисел, общих положений о действительных числах предусматривалось в 7 – 9 классах.

Комплексные числа то включались в школьный курс математики, то исключались из него. Программой 1970 г. комплексные числа были исключены из школьного курса, а программа 1981 г. возвратила их, спустя несколько лет комплексныечисла снова были исключены из курса.

В настоящее время обязательный минимум содержания основных образовательных программ и требования к уровню подготовки выпускников школы регламентируются государственными образовательными стандартами (начального, основного и полного) общего образования. Большинство из существующих ныне разнообразных программ по математики придерживаются традиционной (исторической) схемы введения и расширения числовых систем.

В школьном обучении перед введением новых чисел приводятся обычно примеры практических задач, неразрешимых в известном множестве чисел. Чтобы сделать эти задачи разрешимыми, расширяется имеющееся множество чисел. Например, необходимость введения отрицательных чисел обосновывается обычно с помощью задач, в которых фигурируют направленные величины (как правило, это температура воздуха), изменяющиеся в двух противоположных направлениях, при этом показывается, что неразрешимость этих задач в системе неотрицательных чисел обусловлена тем, что вычитание здесь не всегда выполнимо. Необходимость введения иррациональных чисел чаще всего обосновывается с помощью задач измерения (несоизмеримость измеряемой величины с единицей) и извлечение квадратного корня (из положительных рациональных чисел, не являющимися полными квадратами). К понятию вещественного числа приходят как к числу, представимому в виде бесконечной десятичной дроби (если эта дробь периодическая, то вещественное число – рациональное, если же она непериодическая, то число- иррациональное).

Первая из рассматриваемых задач практическая, вторая – математическая. Легко показать, что первая сводится ко второй. Например, при введении иррациональных чисел достаточно рассмотреть единичный квадрат, измерение его диагонали приводит к извлечению корня квадратного из неполного квадрата. Получается следующая схема обучения: от потребностей практики в разрешимости задач – к потребностям математики в выполнимости операций и от последних – к новым числам, вооружающим математику средствами для удовлетворения потребностей практики.

В сознании учащихся годами складывается историческая схема расширения числовых систем, а одним из результатов общего образования должно быть сформированное представление о логической схеме расширения числовых систем, умение характеризовать их порядковую и алгебраическую структуры согласно логической схеме.