Шестиволновое взаимодействие с удвоенным обращением волнового фронта на тепловой нелинейности в среде с нелинейным коэффициентом поглощения

Интерес к многоволновым процессам (шести-, восьмиволновым и т.д.) обусловлен рядом причин. Во-первых, при распространении нескольких волн в нелинейной среде происходит запись динамических решеток, причем по мере увеличения интенсивности волн наблюдается искажение этих решеток. При дифракции считывающей волны на таких решетках возникают волны, дифрагировавшие в высшие порядки дифракции [1 –5]. С использованием терминологии нелинейной оптики запись динамических решеток и дифракция считывающей волны в первый, второй и последующие порядки дифракции и есть соответственно четырех-, шестиволновое и т.д. взаимодействия. При сильных искажениях записываемых динамических решеток интенсивность шестиволновых процессов может превышать интенсивность четырехволновых процессов. Во-вторых, при больших коэффициентах преобразования наличие волн, дифрагировавших в высшие порядки дифракции, безусловно, оказывает влияние на характеристики волны, дифрагировавшей в первый порядок дифракции. Это необходимо учитывать при использовании четырехволновых преобразователей в системах коррекции фазовых искажений, в системах обработки изображений, временных сигналов. В-третьих, переход к шести-, восьмиволновым взаимодействиям существенно расширяет возможности управления параметрами световых волн, в частности, при шестиволновом взаимодействии можно получить волну с удвоенным обращенным волновым фронтом [6–8].

При многоволновом взаимодействии в поглощающих средах, моделируемых системой энергетических уровней, существенное влияние на характер взаимодействия может оказывать тепловая нелинейность, меняя как амплитудные [9– 10], так и про-

странственные характеристики многоволновых преобразователей.

В настоящей работе исследуются амплитудные и пространственные характеристики шестиволнового преобразователя излучения, осуществляющего удвоенное обращение волнового фронта сигнальной волны, в среде с тепловой нелинейностью и нелинейным коэффициентом поглощения.

1. Вывод уравнений, описывающих связь пространственных спектров взаимодействующих волн

Пусть в плоском слое нелинейной среды толщиной ℓ

распространяются две волны накачки с комплексными

амплитудами A 1 , A 2 и частотами © 1 , © 2 и сигнальная

волна с амплитудой A 3 , частотой © 1 . В результате четы

рех- ( © 1 + © 2 - © 1 = © 1 ) и шестиволнового ( © 1 + © 1 + © 2 -

Уравнения Гельмгольца, описывающие распространение волн в нелинейной среде, имеют вид [11]

V2 + k^ 11 +

I      n 10 .

V 2 + к 2 [ 1 + 251

I    n 20

2 ik1a1 ^ (Д + A3 + к.с.) = 0,

2 ik ₂ а ₂ ^ ( A + A ₄ + A +к .с. ) = 0.

Здесь 5 n = (d n /d T ) 5 T + 0,5(d ² n /d T 2 ) 5 T ² - изменение показателя преломления, обусловленное изменением температуры ( 5 T) при поглощении излучения веществом, к 1 2 = © 1 2 n 1 ₂₀/ c , а 1, ₂ и n i _-20 - коэффициент

поглощения и показатель преломления на частоте © _1-2, d n /d T и d ² n /d T ² – термооптические коэффициенты.

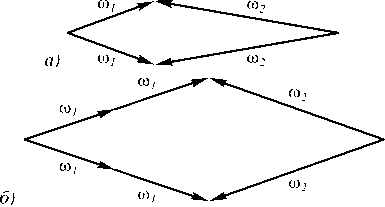
Рис. 1. Схемы четырёхволнового (а) и шестиволнового (б) взаимодействия

Если нелинейная среда моделируется двухуровневой или трехуровневой системой энергетических уровней с учетом возбужденных синглетного и триплетного уровней, то зависимость коэффициента поглощения на частоте ® 1, ₂ от интенсивности излучения есть [12]

а1,2 = а10,20/(1 + Ь111 + Ь2I2) , где 11,2 - интенсивность излучения на частоте w1j2; a1-20 и b 1,2 - начальный коэффициент поглощения и параметр, представляющий собой комбинацию сечений поглощения и скоростей релаксации между энергетическими состояниями на частоте щ1-2.

С учетом интерференции сигнальной волны с первой волной накачки выражение для интенсивности излучения на частоте Щ 1 есть

1 1 = I ‘+ д а * + a A 3 ,

где I‘ = ДА*. Тогда в приближении заданного поля по волнам накачки при малом коэффициенте отражения как в волну с обращенным волновым фронтом (А4| << А3|), так и в волну с удвоенным обращенным фронтом (А6| << |А3|) выражение для коэффициентов поглощения можно переписать следующим образом а1.2 = (а10,20/(1 + J о)) {1 - b1 (A A + А A3)/(1 + J о)+

+ b ( a A * + а A 3 ) ² / ( 1 + J 0 ) ² } .

Здесь J ₀ = b 1 1 ‘ + b ₂ 1 ₂, 1 ₂ = А А * .

Уравнения (1)-(2) дополняются уравнением Пуассона

V ² 5 T + ( a 1 ( 1 ’+ А А * + А * А ₃ ) + a ₂ 1 ₂ ) / Л c p v = 0 .   (5)

Здесь Л - коэффициент теплопроводности, c p - удельная теплоемкость, v - объемная плотность вещества.

Анализ уравнения Пуассона с учетом выражения для коэффициента поглощения (4) показывает, что изменение температуры можно представить в виде суммы быстро ( 5 T₃₁, 5 T * ) и медленно ( 5 T ₀) меняющихся в зависимости от координат составляющих

5 T = 5 Т ₀ +5 T ₃₁ +5 T₃ ‘ +5 T +5 T * . (6)

Изменения температуры 5 T ₃₁ и 5 T₃₁ связаны с наличием в уравнении (5) слагаемых, пропорциональных Д А * и (Д А * ) .

Таким образом, генерация волны с обращенным волновым фронтом обусловлена как изменением показателя преломления 5 n ' = (d n /d T ) 5 T₃₁, так и изменением коэффициента поглощения

^5a 2 = ^a 20 ^b 1 ( А A * ) / ( 1 ⁺ J 0 ) 2 -

Генерация волны с удвоенным обращенным волновым фронтом обусловлена изменением показателя преломления 5 n ‘ = (d n /d T ) 5 T + 0,5(d ² n /d T ² ) 5 T ₃ 2 и изменением коэффициента поглощения

5« 2 = а ₂ 0 b * ( А А * ) ² /2 ( 1 + J 0 ) ³ .

В дальнейшем будем считать, что поглощением излучения на частоте ю ₂ можно пренебречь ( a ₂₀ = 0, b ₂ = 0). Именно такая ситуация реализуется, как правило, в нелинейной среде моделируемой двухуровневой системой энергетических уровней [9].

С учетом вышесказанного уравнения Гельмгольца, описывающие распространение волн накачки, сигнальной и объектных волн, примут вид

{ V ² + k 1² + (2 k, /n ₁₀)((d n /d T ) 5 T ₀ +

+ 0,5(d ² n /d T ² ) 5 T ₀ ² ) - 2 ik ₁( a ₁₀/(1 + b 1 1 ‘ )) } Д,₃ = 0,

L 2.L/2.L² k 2 ( d n_ST Id² n о _T2YL

V + k - +         5 T +     5 T A = 0,

[       ²    n ₂₀ ( d T ⁰ 2d T ^{2   0} Jj

{V2 + k22 + (2 k22/ n 20)((d n/dT )5T0 + 0,5(d2 n /dT2) x x5 T02 }x A4 + (2 k22 / n 20 )(d n /d T )5 T31A2 = 0, l„2 ,2 2k2 [ dn 1 d2n „„2 ]| , V2 + k2 + —2    5 Tn +     5 TA +

2                        U                   U6

I            n 20 ( d T 2 d T Jj

+^ k ² [ dn 5 T ₃‘ + ^1d - n- 5 T ₃ 2 1 A = 0.

n20 (dT 31 2dT231

Уравнение Пуассона распадается на три уравнения

V257* +aw I‘/Л Cp v(1 + b11‘) = 0,(11)

V25T31 +aw ДА* /Л cp v(1 + b11*)2 = 0,(12)

V25T3;-a10 b1 (ДА*)2/Л cp v(1 + b11*)3 = 0.(13)

Из уравнений (9)-(10), (12)-(13) следует, что с учетом рассматриваемых приближений на распространение волны с удвоенным обращенным волновым фронтом не влияет наличие волны с обращенным волновым фронтом. Подробный анализ пространственно-временных, пространственных характеристик волны с обращенным волновым фронтом при четырехволновом взаимодействии на тепловой нелинейности в среде с нелинейным коэффициентом поглощения проведен в работах [13, 14], поэтому в дальнейшем при изучении волны с комплексной амплитудой А 6 наличие в среде волны с комплексной амплитудой А 4 учитывать не будем.

Пусть волны накачки плоские:

4,2 ( r ) = 4 * 1,2 ( z )exp ( - ik 1,2 ⁷ ) •

Сигнальную и объектную волны разложим по плоским волнам

M

4,6 ^{( 7 )} = J 4,6 ^{( K} 3,6 , ^{z )ex}P⁽ - i ^K 3,6 ^p - ^ik 3,6 z z ^{)d K} 3,6 •

—M

Здесь A _3,6 – пространственные спектры сигнальной и объектной волн, k _1,2 – волновые вектора волн накачки, K ₃₆ и k 3 6 _z - поперечная и продольная составляющие волновых векторов k ₃₆, ⁷ { р , z } - радиус-вектор.

Быстро осциллирующие составляющие температуры разложим по гармоническим решеткам

M

5 T ₃₁( ⁷) = J 5 T ₃₁( K _T , z )exp ( — i к _T р ) d K _T ,

—M

M

5 T i (r) = J 5 T ^K t 31 , z )exp ( — i к t 31 р ) d K t 31 ,

—M где 5T31 и 5T31, KT и KT31 - пространственные спектры и волновые вектора изменения температур (температурных решеток).

С учетом приближения медленно меняющихся амплитуд уравнения для амплитуд волн накачки, пространственных спектров сигнальной и объектной волн есть dA1,3 /dz + i (k1 / n10 )((dn /d T )5 T0 +

+ 0,5(d ² n /d T 2 ) 5 T ₀ ² ) A 1, ₃ + ( a ₁₀/(1 + b 1 1 ‘ )) A 1, ₃ = 0 ,

**

*                                     2

⁴ — ik, | d n 5 t ₊ 1 dn 5 t 2 I 4 * = o, d z n ₂₀ ( d T ⁰ 2d T ^{2 0} J

4 — i I * 5 T„ + '   5 T1 IA = dz    n20 (dT 0 2dT2 0 J

= — i — -dn 573'1 4 exp ' i ( k2 z — k6 z ) z ] — n20 dT(16)

k-. d n *   *~/ 7      * 77

^— i Z     _|T? ⁴ I ^{5 T} 31 ^(k T ’ ^z ) ^{5 T} 31 ^{( K} 6 ^{— K} T ’ ^{z ) X}

2n20 dT—M

X exp [— i ( k _{2 z} — k 6 _z ) z ] d K _T .

Уравнение для пространственного спектра волны с удвоенным сопряженным фронтом получено при условии K, = K_T,. + K = K_T + K1 + K = 2 K, + K — K — K‘ .

6 T 31      2 T T 2         1      2      3      3

При выполнении граничных условий

A ( z = 0 ) = Z A 10 , A 2 ( z = ^l ) = A ,, A ( ^K 3 , z = 0 ) =Z A 30 ( ^K 3 )

решения уравнений (14)–(15) есть

A.3 = 4,30 exP [ ^{— C} 1 ^{( z} ) ] , A 2 = ,4 20 exp [ — C 2 ( 1 ) + C 2 ( z ) ] .

Здесь C1 (z) = k j I 4 57 + 1dn 5T02 J dz + Cw(z), n10 0 Id T      2d T ik z I dn        1 d2nI

C2 (z) = П ,,5T0 +^-7^5T0 Idz1, n20 J0 I d T      2d T

z

C 10 ( ^z ) = ^a 10 J ^{(d z} 1 / [ 1 ^{+ b} 1 1 ¹ ( ^z 1 ) ] )•

С учетом граничного условия A 6 ( K 6 , z = I ) = 0 из (16) пространственный спектр объектной волны на передней грани нелинейного слоя имеет вид

A 6 ( K 6 , z = 0) = z 4 6 T ( K 6 , z = 0) + z 4 6 RT ( K 6 , z = 0).

Здесь z46T(K6,z = 0) = i(k2/2n20)(d2n/dT2)z420 X xJJ 5731 (Kt,z)5731 (K6 — Kt,z)x

0 —M

X exp [— i ( k _{2 z} — k _{6 z} ) z ] d K _T d z ,

A RT ( K 6 , z = 0) = i ( k 2 / n 20 >(d n /d T ) z 4 20 X i

^X J ⁵ 7 31 ( ^K 6 ^{— K} 2 , ^z ) exp ^[— i ( ^k 2 z ^{— k} 6 z ) ^z ] ^dz • 0

Пространственный спектр волны с удвоенным обращенным волновым фронтом определяется двумя слагаемыми, одно из которых связано непосредственно с тепловой нелинейностью ( z 4 6 _T ) , а второе слагаемое обусловлено как наличием тепловой нелинейности, так и нелинейным характером изменения коэффициента поглощения (^ 4 6 _RT ) .

Уравнения (18)–(19) дополняются уравнениями для определения пространственных спектров изменения температур 5 T ₃₁ ( K _T , z ) и 5 T' 1 ( K _{T 31}, z ) , полученных из (12), (13) с учетом (17), вида

(d ² 5 7 31 /d z²) — k T 5 7 31 +

A 10 4 X0^ ^[— i ( ^k 1 z ^{— k} 3 z ) z ^— 2 C 10 ^{( z} ) ]         (20)

+--------------------------- 2------------- = 0,

^Л c p ^V ( 1 ^{+ b} 1 1 1 ’ )

d!5 Z 31 __K2 *f'-    ^Ь1^аюA 120   ехпГ-4С

2    кt315T31                   3 exp [ 4C10(z)]X dz               Л Cp v(1+b111)

X J A * 0 ( K 3 )z 4 3 * 0 ( K 3 = 2 K 1 —K 3 —K T 31 ) x            (21)

—M

Xexp[—i(2k1 z — k3z — k3z) z]dK3 = 0, а также уравнением, описывающим изменение интенсивности первой волны накачки, d117dz + (2a10/(1 + b111))I‘ = 0 •                   (22)

Уравнения (20), (21) получены при условии к _T = к 1 — к ₃, к _{T 31} = 2 K 1 —к ₃ — к 3 .

Совместное решение численными методами уравнений (18)–(22) позволяет проанализировать характеристики шестиволнового преобразователя излучения.

• 2.    Обсуждение результатов

При анализе пространственного спектра волны с удвоенным обращенным волновым фронтом будем считать, что пространственный спектр сигнальной волны на передней грани нелинейного слоя меняется по Гауссову закону

A (K3 ) = exp (-K32/K0 ) , где κ0 – параметр, характеризующий расходимость сигнальной волны. В предельном случае (κ0→0,1k) пространственный спектр сигнальной волны соответствует пространственному спектру точечного сигнала.

Для упрощения последующего анализа уравнений (18) – (22) перейдем от трехмерной зависимости пространственных спектров и температурных решеток объектных волн к двумерной.

С учетом выражения для пространственного спектра сигнальной волны уравнение (21), описывающее изменение пространственного спектра температурной решетки, связанное с квадратом интерференционного слагаемого, примет вид d2 5 T1 dz2

^- κ T ²31 ^δ T 3 ^′ 1

-

b ^ .v ^k _x

Λ c_p ν ( 1 + b ₁ I ₁′ ) ³

π k

×        ¹ ₂ exp

2 k ₁ + iz κ ² ₀

к2

- 4 C _w( z ) + i -1- z x ^k i _

× exp

( 2 κ ₁ - κ _{T 31} ) 4 k ₁ κ ² ₀

( 2 k 1 + iz k 0 ) I = 0.

Численный анализ уравнений (18)–(19) с учетом (21)–(23) показывает, что амплитуды пространственных спектров объектных волн А 6 _т и А 6 _RT с увеличением пространственной частоты монотонно уменьшаются (рис. 2).

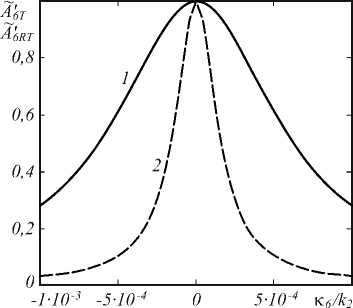
Рис. 2. Нормированные на максимальные значения амплитуды пространственных спектров объектных волн

4 6 _т (I) и А 6 TR (2) при k 1 l = 10⁴ , a ₁₀ l = 1 , k ₂ / k 1 = 2 ,

κ 0 = 0,01 k 1 , b 1 I′(z = 0 ) = 0,05

В качестве характеристик пространственной селективности шестиволнового преобразователя излучения введем полуширины полос пространственных частот ∆κ 6 T и ∆κ 6 RT объектных волн с удвоенным обращенным волновым фронтом, определяемые из уравнений

|A6_T ( к ₆ =Ak _{6 t} , z = 0)| = 0,5| A_T ( K ₆ = 0, z = 0)|,

| A 6 RT ^{( K} 6 = ^Ak 6 RT , ^z = ⁰⁾| = 0,5| A 6 RT ^{( K} 6 = 0, ^z = ⁰⁾| .

Увеличение расходимости сигнальной волны приводит к росту полуширин полос пространственных частот с последующим выходом на установившиеся значения ∆κ ⁰ _{6 T} и ∆κ ⁰ _{6 RT} (рис.3) . Причем ∆κ ⁰ _{6 T} >  ∆κ ⁰ _{6 RT} .

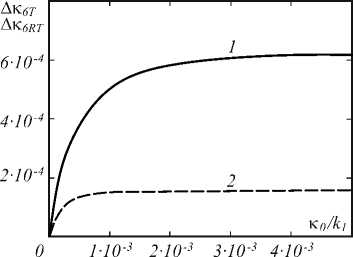
Рис. 3. Зависимость от расходимости сигнальной волны полуширин пространственных спектров объектных волн

^4 6 _T (I) и ^4 6 _RT (2) при k 1 l = 10⁴ , a ₁₀ l = 1 , k ₂/ k 1 = 2

Как следует из уравнений (20), (23), при большой расходимости сигнальной волны κ 0 / k 1 ≥ 10^–2 пространственные спектры температурных решеток перестают зависеть от расходимости сигнальной волны , полностью определяются явлением теплопроводности. Соответственно, от расходимости сигнальной волны перестают зависеть пространственные спектры объектных волн. Нормированные на максимальные значения зависимости пространственных спектров температурных решеток δ T ₃ ′ ₁ от κ T 31 и δ T ₃₁ от κ T совпадают. Однако пространственные частоты κ T 31 и κ T отличаются при κ 1 = 0 в два раза, поэтому пространственный спектр температурной решетки δ T ₃ ′ ₁ у_́же пространственного спектра температурной решетки δ T ₃₁ . Если пространственный спектр объектной волны A _{6 RT} линейно связан с пространственным спектром температурной решетки δ T ₃ ′ ₁ , то пространственный спектр волны A _{6 T} определяется корреляцией пространственных спектров температурной решетки 5 T ₃₁, это и объясняет соотношение между установившимися значениями полуширин полос пространственных спектров этих волн.

При большой расходимости сигнальной волны изменение фаз на полуширинах полос пространственных частот объектных волн ∆κ 6 T и ∆κ 6 RT меньше π / 100.

С ростом интенсивности волны накачки нормированные максимальные значения амплитуд пространственных спектров объектных волн

• ⁽ ^A 6 т =| ^ A 6 T ( ^K 6 = 0, ^z = 0 )| g g 1 ,

A6RT = A6RT (κ6 = 0,z= 0) g2 , где g 1 = (k2 k ia20l5/2 n 20 Ь1(Л Cp v)2)(d2 n /dT2) .420 , g2 = ('Jπk2α10κ0ℓ3/n20Λcpν)(dn/dT)Aɶ20)

вначале возрастают, достигают в окрестности параметра b 1 I ′ ( z = 0), равного единице, наибольшего значения, а затем монотонно уменьшаются (рис. 4). Оптимальное значение интенсивности волны накачки, при которой амплитуда пространственного спектра объектной волны A _{6 T} принимает наибольшее значение, меньше чем оптимальное значение интенсивности волны накачки для объектной волны A _{6 RT} . При этом изменение интенсивности волны накачки в пределах 0,1 ≤ b 1 I ′( z =0) ≤ 10 с точностью ±0,1 % не меняет значения полуширины полос пространственных частот объектных волн.

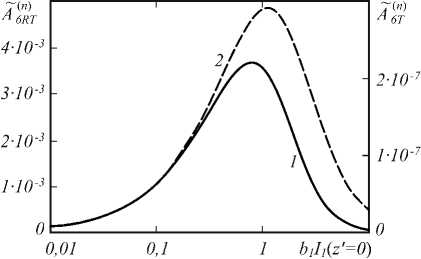
Рис.4. Зависимость нормированных амплитуд пространственных спектров объектных волн A _{6 T} (1) и A ^ɶ _{6 RT} (2) от интенсивности волны накачки при k ₁ ℓ = 10⁴ , α ₁₀ ℓ = 1 , k ₂ Ik ₁ = 2 , κ ₀ = 0, 01 k ₁

С увеличением интенсивности волны накачки возрастает относительный вклад в волну с удвоенным обращенным волновым фронтом объектной волны, наличие которой связано как с тепловой нелинейностью, так и нелинейным характером изменения коэффициента поглощения. Так, при k1ℓ= 104, α10ℓ= 1, k2 / k1 = 2, κ0 = 0,01k1 рост интенсивности волны накачки от b1I′ (z =0) = 1 до b1I′ (z = 0) = 10 приводит к увеличению почти на порядок отношения амплитуд объектных волн A6RT и A6T .

Изменения полуширин полос пространственных частот в зависимости от толщины нелинейной среды хорошо описываются выражениями вида

^∆ κ 6 T ,6 RT

⁼ a T , RT

/ ℓ + b   k

T , RT 2

где α T,RT и b T,RT – коэффициенты пропорциональности, значения которых слабо зависят от коэффициента поглощения и в основном определяются отношением волновых чисел взаимодействующих волн. При k 1 = 10⁵ см^–1, α 10 / k 1 = 10^–5, k 2 / k 1 = 2 в области изменения толщины нелинейной среды от 2 мм до 5 см a T = 12,56, a RT = 3,22, b T =1,22 ⋅ 10^–6, b RT =0.

В качестве примера рассмотрим шестиволновое взаимодействие с удвоенным обращением волнового фронта в водно-спиртовом растворе эозина при записи температурных решеток излучением на длине вол- ны 1,06 мкм в слое толщиной ℓ= 1,25 мм (dn /dT = 4⋅10–4 град-1, d2n /dT2= 10–7 град–2 n10=1,36, b1 = 10–24 (с∙м2) / фотон, Λcp = 3⋅10–1Дж /(м·с·град) [9], [15]). При концентрации молекул эозина N = 8⋅1017 см–3, σ21 = 1017 см2       коэффициент поглощения

α 10 = N σ 12 = 8 см^–1. При малой интенсивности волны накачки ( b 1 I ′ ( z = 0) ≤ 0,1) и расходимости сигнальной волны κ 0 / k 1 = 10^–2 отношение максимальных значений амплитуд пространственных спектров объектных волн A _{6 TR} и A _{6 T} равно 3 ⋅ 10³. Таким образом, волну с удвоенным обращенным волновым фронтом при шестиволновом взаимодействии на тепловой нелинейности в водно-спиртовом растворе эозина определяет объектная волна A 6 TR . Наибольшее значение амплитуда пространственного спектра этой волны принимает при интенсивности волны накачки, равной 19 Вт/м². При этом полуширина полосы пространственных частот ∆κ RT = 2,4 ⋅ 10³ м^-1.

Заключение

Рассмотрен вклад в волну с удвоенным обращенным волновым фронтом как объектной волны, связанной непосредственно с тепловой нелинейностью, так и объектной волны, наличие которой обусловлено как тепловой нелинейностью, так и нелинейным характером изменения коэффициента поглощения . Найдена зависимость амплитуд пространственных спектров объектных волн от интенсивности волны накачки. С увеличением интенсивности волны накачки возрастает вклад в волну с удвоенным обращенным волновым фронтом объектной волны, связанной непосредственно с нелинейным характером коэффициента поглощения. Показано, что при большой расходимости сигнальной волны полуширина полосы пространственных частот объектной волны , связанной с нелинейным характером коэффициента поглощения, в несколько раз меньше полуширины полос пространственных частот объектной волны , связанной только с тепловой нелинейностью. Изменение интенсивности волн накачки не влияет на полуширины полос пространственных частот объектных волн. Найдены зависимости полуширин полос пространственных частот объектных волн от толщины нелинейной среды.