Шестиволновое взаимодействие в многомодовых волноводах с керровской нелинейностью с учетом гауссовой структуры волн накачки

По сравнению с трех-, четырехволновыми преобразователями излучения шестиволновые преобразователи излучения обладают большими возможностями управления формой волнового фронта, пространственной фильтрации, преобразования изображения, передачи информации с одних пучков на другие и т.д. [1 –7].

Для повышения эффективности (коэффициента отражения), как и при четырехволновом взаимодействии [8– 13], целесообразно и шестиволновое взаимодействие рассматривать в волноводах [14].

Многоволновое взаимодействие в волноводах по сравнению с взаимодействием в неограниченных в поперечном направлении средах характеризуется по крайней мере двумя особенностями: 1) выполнение условий фазового синхронизма при переходе от непрерывного набора мод, на которые раскладываются амплитуды взаимодействующих волн, к дискретному набору накладывает часто более жесткие требования на номера мод взаимодействующих волн; 2) изменяется роль волн накачки. В нелинейной среде с неограниченными в поперечном направлении размерами пространственная структура волн накачки на гранях нелинейной среды определяет объем нелинейной среды, в которой происходит эффективное многоволновое взаимодействие. В волноводе объем взаимодействия определяется в основном геометрическими размерами самого волновода. Пространственная структура волн накачки на гранях волновода определяет распределения амплитуд волн накачки по поперечному сечению волновода.

При использовании многоволновых преобразователей излучения в системах коррекции фазовых искажений для обработки изображений в реальном масштабе времени необходимо знание соответствия между комплексными амплитудами падающей (сигнальной) на преобразователь и отраженной или прошедшей (объектной) волн [15]. Задача о нахождении однозначной связи между комплексными амплитудами объектной и сигнальной волн имеет решение лишь в приближении заданного поля по волнам накачки. В этом случае многоволновой преобразователь излучения можно рассматривать как линейный фильтр пространственных частот [16] и, используя, например, метод функции размытия точки (ФРТ), найти однозначную связь между комплексными амплитудами сигнальной и объектной волн [17].

В настоящей работе в приближении заданного поля по волнам накачки с учетом пространственной структуры волн накачки методом ФРТ анализируется качество обращения волнового фронта (ОВФ) при шестиволновом взаимодействии в многомодовых двумерных волноводах с керровской нелинейностью. В качестве волноводов рассматриваются волновод с бесконечно проводящими поверхностями и градиентный волновод с параболическим профилем показателя преломления (параболический волновод).

1. Вывод выражения для функции размытия точки шестиволнового преобразователя излучения

Имеется волновод с керровской нелинейностью, расположенный между плоскостями z =0 и z = l . В волноводе навстречу друг другу распространяются две волны накачки с комплексными амплитудами A 1 , A 2 и сигнальная волна с комплексной амплитудой A 3 . В среде в результате вырожденного шестиволнового взаимодействия й + и - и + и - и = и наводится нелинейная поляризация P нл ~ ( A 12 A 1 * A 2 + A 1 A 2 A 2 * ) A 3 * , которая выступает как источник объектной волны с комплексной амплитудой A 6 , сопряженной амплитуде сигнальной волны и распространяющейся ей навстречу.

В приближении заданного поля по волнам накачки, без учета изменения показателя преломления из-за распространения волн накачки, при малом коэффициенте преобразования (| A 6 | << | A 3 |) система уравнений, описывающая распространение волн накачки, сигнальной волны, генерацию волны с обращенным волновым фронтом, имеет вид [17– 18]:

[V ² + k ² n ² ( x ) ] A i,2,3 = 0,

[V ² + k ² n ² ( x ) ] A = - g ( A ² A * A 2 + A A 22 A 2 ) A * .

da NNNNN

2iвr     = gX X X XXaipaip'a*p'a2ma3*s x dz       p=0 p '=0 p ‘=0 m=0 s=0

^xy pp ' p"msr ^{exp [—} i A pp ' p’msr^z J ⁺

NNN NN

+gXXXXXaipa2ma2m'a2m''a3s Х p=0 m=0 m '=0 m '=0 s=0

^xy pmm ' m"sr ^{exp [—} i ^A pmm ' m"sr^z J

Здесь

У ppp'msr = J fp (x) fp' (x) f„ ■ (x) fm (x) fs (x) Х fr (x) dx - интеграл перекрытия, характеризующий эффективность взаимодействия шести мод волновода,

^A pp ' p " msr P p ^{+ в} p ' ^в p "  ^в m ^в s ^{+ в} r ,

Apmm' m " sr вp в m в m' + в m " в s + в r волновые расстройки.

С учетом граничного условия a 6r (z = £) = 0, проинтегрировав правую и левую части выражения (5) по продольной координате z, получим igf " " "ЛЛ a 6 r (z = 0) = - —XX X XXYpp'p' msraipaip' x 2вr p=0 p'=0 p'=0 m=0 s=0

Здесь g 240 n k ² x ⁽⁵⁾, x ⁽⁵⁾- нелинейная восприимчивость пятого порядка, k = и / c, и - циклическая частота, n ( x ) -показатель преломления, x – поперечная координата.

Пусть модами волновода являются функции:

f m ( x, z ) = fm ( X ) exp( - i в m Z ) •                       (2)

Здесь p m - постоянная распространения m -й моды волновода, z – продольная координата.

Разложим комплексные амплитуды взаимодействующих волн по модам волновода:

N

Ai (x, z) = X aip (z) fp (x)exP(—iвpZ), p=0

N

A 3 ( x , Z ) = X a 3 s ( z ) f s ( x )exp( - i в s Z ), s = 0

N

A2 (x, z) = X a2m (z) fm (x) exp(iвmz), m=0

N

A ( x , z ) = X a 6 r ( z ) fr ( x ) exp( i в r z ), r = 0

где a jn ( z ) – коэффициенты разложения волн накачки, сигнальной и отраженной волн по модам, N – число мод волновода, учитываемых в разложении. Из системы уравнений (1) следует, что коэффициенты a jn ( z ), j = 1,2,3, не меняется вдоль оси Z.

В приближении медленно меняющихся амплитуд из (1) с учетом разложения взаимодействующих волн по модам волновода уравнение, описывающее изменение вдоль оси Z коэффициентов в разложении амплитуды волны A 6 ( x , z ) по модам волновода, можно записать следующим образом:

*         * ■    f App'p'msrf |      [ ■ App'p'msrf xaip’a2ma3ssinc I ----I exp I -i     2----

NNNNN

- XXXXX y 2 ^в r p = 0 m = 0 m '= 0 m'=0 s = 0

x sinc

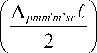
exp I ^- i

*             -.*

pmm ' m ' sr a ip a 2 m a 2 m ' a 2 m' a 3 s ^Х

^A pmm ' m 'sr'

Зная выражение для коэффициента a 6 r , найдем амплитуду объектной волны на передней грани волновода:

л p m N pp \     g f N f r ( x )

A (x,z=0) = x a 6 rfr(x,) = - i—X     Х r=0                     2 r=1 в r

NNNNN

Х

XXXXX y

p = 0 p '= 0 p '= 0 m = 0 s = 0

*           -.*

pp’p’msr a ip a ip ' a i p’ a 2m a 3 s ^Х

■ I ^A pp'p'msr ^f | ^f . ^A pp'p^rnrr ^f | . x sinc —--- exp - i—^ --- +

I 2 J I 2 J

NNNNN

+ XX X X X a i p a 2 m^a 2 m a 2 m ' a 3 s У pmm^!m’'sr ^Х p = 0 m = 0 m’ = 0 m'=0 s = 0

х sinc

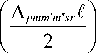
exp I - i

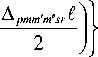
Пусть сигнальная волна – это волна от точечного источника, расположенного на передней грани волновода на расстоянии x 0 от оптической оси,

A ₃( x , z = 0) = 8 ( x - x ₀ ) .

Тогда выражение для коэффициента a 3 r в разложении амплитуды сигнальной волны по модам волновода можно представить в виде:

a 3 s ( z = 0 ) = j f_s ( x ) A 3 ( x , z = 0) dx = f s ( x 0 ).          (8)

в r = { к ² П 1 ² - q 2 } ^1/2,

Подставив (8) в (7), получим выражение, описывающее преобразование точечного сигнала (функция размытия точки (ФРТ)) вида

g ^ N J ( x )

G ⁽ x, x o , z = 0) = - i — > 1. -p— x

NNNNN x^EEEEEypp'p " msra1 pal p' al p "a 2 mfs ( xo) X

[ p = 0 p '= 0 p ’= 0 m = 0 s = 0

x sinc I ^{X p} 'm ^J | exp | - i ^ ppvmr L | +

I 2 J 4    2 J

где q 2 = 2(2 r + 1)/ ю 2 - для параболического волновода, q r =[л ( r + 1 )/2 a ] - для волновода с бесконечно проводящими поверхностями.

Из условий фазового синхронизма (10) следует связь между номерами мод взаимодействующих волн вида: в волноводе с бесконечно проводящими стенками

NNNNN

+ EX > E > a i p a 2 m a 2 m a 2 m f s ( x 0 ) Y

p = 0 m = 0 m' = 0 m ’= 0 s = 0

pmm'm’sr

^Л pmm'm’sr = ⁰ ^ ( p ^{+ 1} ) ^-( m ^{+ 1} ) ^-( m ' ^{+ 1} ) ⁺ + ( m” + 1 ) ² - ( s + 1 ) ² + ( r + 1 ) ² = 0,

^Л pp ' p ’ msr = ⁰ ^ ( Р ^{+ 1} ) ⁺( Р' ^{+ 1} ) ^-( Р ” ^{+ 1} ) ^- - ( m + 1 ) 2 - ( s + 1 ) 2 + ( r + 1 ) 2 = 0,

■ f ^Л pmm’m'sr ^ X Sinc —-----

exp l ^- i

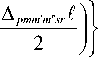
Будем рассматривать длинные волноводы, т.е. считаем, что при условии Л ppp '„sr * 0, Л pmm m "_sr * 0, Л _Рр p'msr I >> 1, Лр„„ ’_m ' sr I >> 1. Тогда основной вклад в выражение для комплексной амплитуды объектной волны дают слагаемые, для которых выполняются условия

^Л pp'p’msr   ⁰ , ^Л pmm'm’sr   ^0.

Это условия фазового синхронизма для шестиволнового взаимодействия. Условие фазового синхронизма уменьшает число сумм, входящих в выражение (9), устанавливает связь между номерами шести взаимодействующих мод волновода.

2. Обсуждение результатов

В качестве волноводов рассмотрим двумерный волновод с бесконечно проводящими поверхностями, расположенными на расстоянии 2 а друг от друга, заполненный средой с показателем преломления n 1 , и двумерный волновод с параболическим профилем показателя преломления:

n ² ( x ) = n 2 Г 1 - 2 е ₂ ( x/x q ) 2

s ₂ и x q - параметры, характеризующие волновод.

Модами волновода с бесконечно проводящими поверхностями являются функции

f ( x ) = ^sin a

п ( r + 1 )

2 a

( x + a )

Модами параболического волновода являются

функции Гаусса–Эрмита [19].

^fr ^{( x} ) =

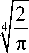
4 2 ^rr ! ® 0

H r

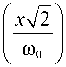
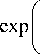
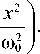
Здесь H_r ( x V2"/ю₀) - многочлен Эрмита r -го порядка, ю 0 = (2 x q )/( kn ₁(2 s ₂ )^1/2). Постоянная распространения r -й моды волновода есть

в параболическом волноводе

Л _pmm ' _m ’ _sr = 0 ^ p - m - m ' + m” - s + r = 0,   (16)

Л pppmsr = 0 ^ p + p’ - p ’ - m - s + r = 0.    (17)

Если обе волны накачки одномодовые и возбуждают нулевую моду волновода, выражение для ФРТ принимает вид

G 0 ( x , x 0 , z = 0) = - ig- ( a 30 a 20 + a 10 a 20 ) x k

N

^: E fr ( x ) f_r ( x 0 ) Y 0000 rr .

r = 0

На рис. 1 для шестиволновых преобразователей излучения в волноводе с бесконечно проводящими поверхностями (рис. 1 а ), в параболическом волноводе (рис. 1 б ) приведены нормированные на максимальное значение ( G = G ( x , x ₀ = a , z = 0)/ G m _ax|, G max - максимальные значения функции) зависимости модулей ФРТ от поперечных координат. При расчете ФРТ учитывалось 30 мод волновода. Вид модулей ФРТ типичен для многомодовых преобразователей излучения в средах с керровской, тепловой, резонансной нелинейностями [17] – увеличение поперечной координаты приводит к уменьшению (монотонному или осциллирующему) модуля ФРТ.

Пусть первая волна накачки возбуждает нулевую моду волновода ( p =0), а вторая волна накачки многомодовая. Тогда ФРТ шестиволнового преобразователя излучения в параболическом волноводе есть

G ₁( x , x ₀, z = 0) = - ig- x

X L3 УУ ^fr = s + m ⁽ x ) у ₍ f(_X\ ₊ ^X ] ^a 10 EE о       ^Y 000 ms ( s + m ) a 2 mjs ^{( x} 0 ) ⁺

I m = 0 s = 0 ^p r = s + m

NNNN

+a10EEEE R m=0 m'=0 m "=0 s=0   P;

ГЫ fs+m+m' - m"

¹ s + m + m' - m"

^X a 2 m a 2 m' a 2 m" ^fs ⁽ x 0 ) } .

( x )

^Y 0 mm'm"s ( s + m + m' - m ’ ) ^X

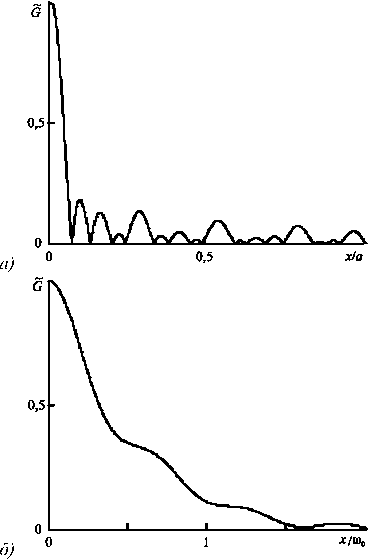
Рис. 1. Вид модулей ФРТ шестиволновых преобразователей в волноводе с бесконечно проводящими поверхностями (а), в параболическом волноводе (б) при одномодовых волнах накачки (p=m=0)

Выражение для ФРТ шестиволнового преобразователя излучения в волноводе с бесконечно проводящими стенками совпадает с выражением для ФРТ шестиволнового преобразователя излучения в параболическом волноводе (19) при условии, что в первой сумме номер моды объектной волны находится из условия

( r + 1 ) 2 = ( m + 1 ) 2 + ( s + 1 ) 2 - 1,                     (20)

а во второй сумме из условия

(r + 1)2 = (s + 1)2 + (m + 1)2 + (m‘ + 1)2 —(m’ + 1)2 -1. (21)

Если вторая волна накачки одномодовая и возбуждает основную моду волновода ( m =0), а первая волна накачки многомодовая, тогда выражение для ФРТ шестиволнового преобразователя излучения в параболическом волноводе запишется следующим образом

G ₂( x , x ₀, z = 0) = - ig- x

N N N N f *\ a 20 XX XX f_R I      p = 0 p '=0 p ’= 0 s = 0 P

x a 1 p a 1 p a ip f s ( x 0 ) +

NN

+ a 230 EX p = 0 s = 0

- p - p '+ p • ⁽ x )

1 0 ppp ■s ( s - p - p '+ p ') ^x ’ s - p - p '+ p '

^fr = s - p ⁽ x ) P r = s - p

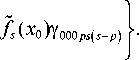
Если шестиволновое взаимодействие реализуется в волноводе с бесконечно проводящими стенками, то в первой сумме выражения (22) номер моды объектной волны находится из условия

( r + 1 ) ² = ( s + 1 ) ² - ( p + 1 ) ² - ( p ' + 1 ) ² + ( p + 1 ) ² + 1,(23) а во второй сумме из условия

( r + 1 ) ² = ( s + 1 ) ² - ( p + 1 ) ² + 1. (24)

Качество ОВФ шестиволновым преобразователем излучения будем характеризовать полушириной центрального максимума ФРТ, расположенной на оси волновода ( A x ), определяемой из решения уравнения [10],

| G ( x = A x , x ₀ = 0, z = 0)| = 2 G ( x = 0, x ₀ = 0, z = 0). (25)

При условии, что обе волны накачки одномодовые с нулевыми номерами мод, полуширина модуля ФРТ четырехволнового преобразователя излучения в волноводе с бесконечно проводящими стенками A x = 0,039 a , в параболическом волноводе A x = 0,031 ю ₀ .

• 2.1.    Параболический волновод

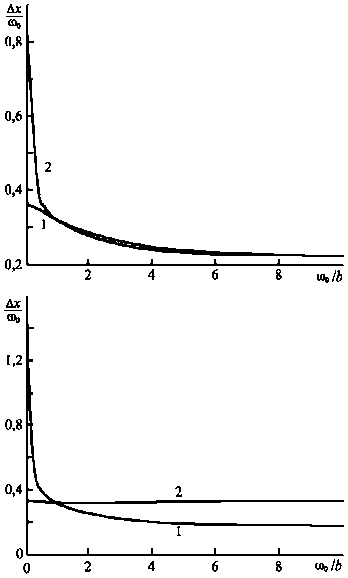
На рис. 2 для шестиволнового преобразователя в волноводе с параболическим профилем показателя преломления приведены зависимости нормированных полуширин модулей ФРТ, расположенной на оси волновода, от нормированной ширины волны накачки при условии, что одна из волн накачки возбуждает нулевую моду волновода, а распределение амплитуды другой волны накачки на грани волновода описывается гауссовой функцией ( A 1 ( x , z =0)=exp(– x ²/ b ²) или ( A 2 ( x , z = ℓ ) =exp (– x ²/ b ²), здесь b – ширина волны накачки).

При A A i >>  A ₂ A i для шестиволнового преобразователя излучения как при уменьшении ширины второй гауссовой волны накачки при условии возбуждения первой волной накачки моды волновода с нулевым номером, так и при уменьшении ширины первой гауссовой волны накачки при условии возбуждения второй волной накачки моды волновода с номером m =0 наблюдается уменьшение полуширины модуля ФРТ (рис. 2 а ). Качество ОВФ улучшается. Причем в интервале 01 ю ₀ <  b <  ю ₀ значения полуширин модулей ФРТ как в случае одномодовой первой волны накачки и многомодовой второй волны накачки, так и в случае одномодовой второй волны накачки и многомодовой первой волны накачки с точностью 4 % совпадают. В интервале ю ₀ <  b <  10 ю ₀ скорость изменения полуширины модуля ФРТ с увеличением ширины пучка накачки в случае одномодовой первой волны накачки и многомодовой второй волны накачки оказывается меньше, чем в случае одномодовой первой волны накачки и многомодовой второй волны накачки .

При A A* << A2 A2 для шестиволнового преобразователя излучения уменьшение ширины пучка второй гауссовой волны накачки при условии возбуждения первой волной накачки моды волновода с номером p =0 уменьшает полуширину модуля ФРТ.

а)

б)

Рис. 2. Зависимость нормированной полуширины модуля ФРТ от нормированной ширины волны накачки.

Интенсивности волн накачки: A 1 A >>  A 2 A 2 (а),

A A <<  A 2 A ₂ ’ (б). Первая волна накачки возбуждает нулевую моду волновода, амплитуда второй волны накачки меняется по гауссовому закону (1); амплитуда первой волны накачки меняется по гауссовому закону, вторая волна накачки возбуждает нулевую моду волновода (2)

Однако в случае, когда амплитуда первой волны накачки на передней грани волновода меняется по гауссову закону, а вторая волна накачки возбуждает нулевую моду волновода, уменьшение ширины пучка накачки практически не меняет полуширину модуля ФРТ.

В табл. 1 приведены максимальное и минимальное значения полуширин модулей ФРТ в диапазоне изменения ширины волны накачки 0125 ® ₀ <  b <  5 ® ₀

Табл. 1. Максимальное и минимальное значения полуширин модулей ФРТ шестиволнового преобразователя в волноводе с параболическим профилем показателя преломления

	Первая волна накачки	Вторая волна накачки	Максимальное значение полуширины	Минимальное значение полуширины
A i A i >>  A 2 A	одномодовая	гауссова	0,358 ® 0	0,226 ® 0
	гауссова	одномодовая	0,687 ® 0	0,225 ® 0
A A i <<  A 2 A i	одномодовая	гауссова	0,881 ® 0	0,183 ® 0
	гауссова	одномодовая	0,331 ® 0	0,332 ® 0

Сравнение минимальных значений полуширины модулей ФРТ шестиволновых преобразователей излучения в параболическом волноводе показывает, что среди рассмотренных случаев наилучшее качество ОВФ будет наблюдаться при A 1 A i <<  A 2 A 2 и условии, что первая волна накачки одномодовая с нулевым номером моды, а распределение амплитуды второй волны накачки на задней грани волновода описывается гауссовой функцией, изменение ширины которой позволяет изменять разрешающую способность шестиволнового преобразователя излучения, оцениваемую по полуширине модуля ФРТ.

В случае A 1 A i >>  A₂ A 2 , когда первая волна накачки одномодовая, а вторая волна накачки многомодовая, ФРТ шестиволнового преобразователя излучения можно представить в виде когерентной суммы ФРТ, соответствующих одномодовым волнам накачки,

N

Gi( x, x о, z = 0) = £ G0 m (x, x 0, z = 0),(26)

m = 0

где

G 0 m ( x , x 0 , Z = 0) =

. g£ „3    N 77

i ~    a 10 a 2 m / , ^fr ⁽ x ) fr- m ⁽ x 0 ) ^Y 000 mr ( r - m )

2 knir

В функциях G 0 m ( x , x 0 , z =0) отсутствуют моды волновода с номерами от 0 до m -2. При условии, что первая волна накачки возбуждает нулевую моду волновода, увеличение номера моды второй волны накачки приводит к сужению ширины центрального максимума модуля функций G 0 m ( x , x 0 =0, z =0), возрастанию величины боковых максимумов (рис. 3). По мере отклонения от единицы отношения ® ₀ / b увеличивается вклад в выражении (26) ФРТ, соответствующих одномодовым волнам накачки с неравными номерами мод. Причем при b <  ® ₀ центральные максимумы этих функций складываются синфазно, а при b >  ® ₀ - в противофазе. Это объясняет улучшение качества ОВФ с уменьшением ширины пучка накачки. Сходный характер зависимости полуширины модуля ФРТ от ширины пучка гауссовых волн накачки наблюдается и для четырехволнового преобразователя излучения [20].

Аналогично выражение для ФРТ шестиволнового преобразователя излучения в виде когерентной суммы ФРТ, соответствующих одномодовым волнам накачки, можно представить и в случае A1 Ai << A2 A2, когда вторая волна накачки возбуждает одну моду волновода, например, с номером m =0, а первая волна многомодовая. В этом случае ФРТ, соответствующие одномодовым волнам накачки, есть g^    N

G 2 p ( x , x 0 , z = 0) = - i —— a 2 ³ 0 a i p > f_r ( x ) x

2 kn i       Г : 0                  (27)

^x f r + p ^{( x} 0 ) ? 000 pr ( r + p ) .

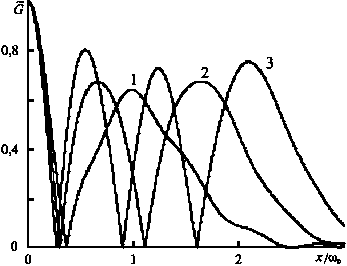
Рис. 3. Нормированные на максимальное значение модули ФРТ шестиволнового преобразователя излучения в параболическом волноводе, соответствующие одномодовым волнам накачки с номерами мод p = 0, m=2(1), 4(2), 6(3)

2) номер моды сигнальной волны равен нулю ( s =0), совпадают номера мод объектной волны и второй волны накачки ( r = m ).

Численный анализ выражения (27) показывает, что в диапазоне изменения ширины первой гауссовой волны накачки 0,1 ю ₀<  b < 10 ю ₀ имеем

I G 2 p ( x , x о , z = 0)| <<| G 2о ( x , x 0 , z = 0)|, p = 2,4,...

Табл. 2. Максимальное и минимальное значения полуширин модулей ФРТ шестиволнового преобразователя в волноводе с бесконечно проводящими поверхностями

	Первая волна накачки	Вторая волна накачки	Минимальное значение полуширины	Максимальное значение полуширины	^ , %
A A >>  A 2 A 2	одномо довая	гауссова	0,039 a	0,041 a	5,1
	гауссова	одномо довая	0,038 a	0,046 a	20,5
A, A <<  A 2 A 2	одномо довая	гауссова	0,038 a	0,048 a	25,6
	гауссова	одномо довая	0,039 a	0,044 a	12,6

Так, например, при ю ₀/ b = 3 отношение максимальных значений модулей функций G 2 p и G 20 составляет при p =2,4,6 соответственно 0,12, 0,04, 0,02. Это объясняет слабую зависимость ширины модуля ФРТ шестиволнового преобразователя излучения от ширины первой гауссовой волны накачки.

2.2. Волновод с бесконечно проводящими поверхностями

Для шестиволнового преобразователя излучения в волноводе с бесконечно проводящими поверхностями изменение ширины одной из гауссовых волн накачки при условии возбуждения второй волной накачки нулевой моды волновода в диапазоне 0,125 a <  b <  5 a независимо от соотношения интенсивностей волн накачки слабо меняет полуширину модуля ФРТ (табл. 2). Относительное изменение полуширины модуля ФРТ, оцениваемое как

£, = (Axmax — Axmin ) / Ax0,

Тогда выражение для ФРТ (19) можно записать следующим образом

G ( 1 ) ( x , x ₀ = 0, z = 0) = - i -g— a i³₀ x 2 kn 1

N T²⁰ -^lr

N

+ £ a 2 r sin r = 2

n( r +

2 a

n( r +1)

2 a

( x + a ) sin

n ( r n

7 0000 rr + ⁽²⁸⁾

( x + a ) Y 0000rr ’ •

где A x _max, A x min - максимальное и минимальное значение полуширины модуля ФРТ на рассматриваемом диапазоне ширин волны накачки, A x 0 - значение полуширины модуля ФРТ при одномодовых волнах накачки ( p = m =0) в рассмотренных случаях меняется от 5,1 % до 25,6%.

Остановимся на случае A 1 A ^ >>  A ₂ A ₂ * , когда происходит изменение ширины второй гауссовой волны накачки при условии возбуждения первой волной накачки в волноводе нулевой моды.

Для этого случая условие фазового синхронизма (20) выполняется при двух условиях:

1) номер моды второй волны накачки равен нулю ( m =0), а номера мод сигнальной и объектной волн совпадают ( r = s );

В случае A ₂ A 2 >>  A 1 A 1 * , когда первая волна накачки многомодовая, а вторая волна – одномодовая ( m = m' = m" = 0), условие фазового синхронизма (24) может быть выполнено, если:

• 1)    номер моды первой волны накачки равен нулю ( p =0), а номера мод сигнальной и объектной волн совпадают ( r = s );

• 2)    номер моды объектной волны равен нулю ( r =0), совпадают номера мод сигнальной волны и первой волны накачки ( s = p ). В этом случае выражение для ФРТ запишется следующим образом

G 2 ^{2 )} ( x , x 0 = 0, z = 0) = - i -^g— a 20 x 2 kn ₁

N

4 a ¹⁰ -^

+ sin

n( r +1)

2 a

(x + a)

sin

n( r +1)

Y 0000 rr + (29)

—(x - a) 2a

N

£ a 1 p sin

P = 2

^П( P ⁺ 1 )

^Y 0000 pp

Численный анализ выражений (28), (29) показывает, что величины первых слагаемых, значения которых определяет нулевая мода второй (первой) волны накачки, намного превосходит значение второго слагаемого, зависящего от коэффициентов высших мод в

разложении амплитуды второй (первой) волны накачки по модам волновода. Так, например, для функции G 22 ) отношение максимальных значений модулей второго и первого слагаемых составляет 0,042. Это объясняет слабую зависимость полуширины модуля ФРТ от ширины гауссовой волны накачки.

Заключение

С использованием метода ФРТ в приближении малого коэффициента отражения проанализировано качество ОВФ шестиволновыми преобразователями излучения в многомодовых волноводах (параболическом, с бесконечно проводящими поверхностями) с керровской нелинейностью с учетом гауссовой пространственной структуры волн накачки.

Показано, что при шестиволновом взаимодействии в волноводе с бесконечно проводящими поверхностями при условии, что одна волна накачки возбуждает нулевую моду волновода, а распределение амплитуды другой волны накачки на грани волновода меняется по гауссову закону, ширина волны накачки слабо влияет на качество ОВФ. Сходная ситуация наблюдается для шестиволнового преобразователя излучения в параболическом волноводе при условии, что интенсивность второй накачки намного больше интенсивности первой волны накачки, вторая волна накачки возбуждает нулевую моду волновода, а распределение амплитуды первой волны накачки в зависимости от поперечной координаты меняется по гауссову закону.

В случае, когда интенсивность первой волны накачки намного превосходит интенсивность второй волны накачки, полуширина модуля ФРТ шестиволнового преобразователя в параболическом волноводе с уменьшением ширины гауссовой волны накачки уменьшается. Качество ОВФ улучшается.

Заметим, что объяснение полученных результатов, используя представление ФРТ шестиволнового преобразователя излучения в волноводе в виде когерентной суммы ФРТ, соответствующих одномодовым волнам накачки, возможно лишь в случае, когда волна накачки, амплитуда которой входит в выражение для нелинейной поляризации среды в третьей степени, возбуждает одну из мод волновода, а многомодовой является волна накачки, амплитуда которой входит в выражение для нелинейной поляризации среды в первой степени.