Щелевые дифракционные экраны для минимизации волновых полей

Одной из актуальных задач при волновой передаче информации является подавление помеховых полей, оказывающих мешающее влияние на работу различных систем. При решении этой задачи получили признание вынесенные экраны [1–5]. Достоинством таких экранов является то, что они не оказывают существенного влияния на характеристики антенной системы и потому не требуют внесения в нее каких-либо конструктивных изменений. В работе исследуется класс экранов прямоугольной формы, имеющих большую протяженность в одном направлении и непрерывные щелевые прорези в этом направлении по всей длине. Благодаря этой особенности такие экраны при удачном выборе размеров щелей и полосок обеспечивают широкую область подавления в данном направлении.

Идея использования щелевых экранов выдвинута впервые в [1], затем развивалась в [2–4]. Исследования направлены в основном на выбор оптимальных параметров, что понятно с точки зрения повышения эффективности и инженерной реализуемости создаваемых конструкций. Однако в случае экранов с произвольном числом щелей сложность их оптимизации определяется большим числом искомых параметров, входящих в уравнение целевой функции. Поэтому в указанных работах достигнутая степень подавления помехового поля либо невысока (~15 дБ) [3, 4], что говорит о несовершенстве методов оптимизации, либо она получена в простейшем случае [2] (падение плоской волны, когда экран имеет одну щель и симметрию относительно ее середины), что свидетельствует об ограниченной области его применения.

В данной работе ставилась задача: разработать достаточно эффективный метод выбора оптимальных параметров щелевых экранов для локального подавления помеховой волны и исследовать пространственную структуру областей подавления, создаваемых вблизи точек максимального ослабления.

В качестве обобщенного экрана выбирается k – щелевой экран, имеющий симметрию относительно середины центрального экрана (рис. 1), а в качестве целевой – функция Ф, имеющая значение множителя дифракционного ослабления.

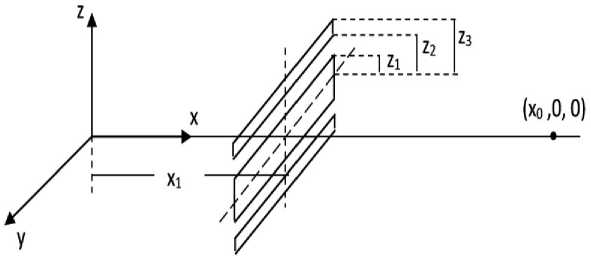
Рис. 1. Геометрия и задачи

Уравнение целевой функции включает в себя условие абсолютной минимизации поля Ф = 0 в точ-

ке (x0, 0, 0). В векторной записи уравнение целевой функции представится в виде:

2k + 1 ,       . -  .

где

Ф = E( - 1 ) ^{J - 1} • a (u j ) = 0, J = 1

| a (U j ) I = _A/l^C( J - S(u JJ )J⁷ + C(^

^ ^{( u} j ) = arctg^ модуль и фаза векторной функции a (_v ) , _v =

C(u j ) - S(u j )

–

- C(u j ) - S(u j )

2 _z b – параметр Френеля, а С(υ j ) и S(υ j ) – из-

вестные интегралы Френеля, b – радиус первой зоны Френеля.

Уравнение целевой функции в виде (1) содержит 2к неизвестных параметров υj и даже в простейшем случае однощелевого экрана имеет 2 неизвестных параметра при одном заданном. Если к этому добавить, что вид векторной функции a (Uj) достаточно сложен, то непосредственное аналитическое решение данного уравнения не представляется возможным. Поэтому оставался единственный вариант поиска эвристических способов решения исходного уравнения. В результате поиска разработан способ решения уравнения целевой функции, в равной степени использующий аналитические идеи и численные приемы с графическими построениями. В основу способа заложено использование свойств годографа векторной функции а (и.) для нахождения значений параметров uj, удовлетворяющих заданному уравнению (1). Векторная функция a (и ), задаваемая формулами (2) и (3), описывает дифракцию от прямолинейного края (от полуплоскости), соответствующего j-й кромке щелевого экрана. Поэтому в уравнении (1) осуществляется суммирование 2k + 1 таких векторных вкладов, причем чередование знака определяет по принципу Гюйгенса с учетом затененных и свободных областей.

В разработанном способе используются оптимизатор, состоящий из годографа векторной функции а (и ) , предварительно рассчитанный и построенный на плоскости, и механизм плоскопараллельного перемещения линеек, осуществляющий операцию векторного суммирования и выявления тех векторов, которые удовлетворяют уравнение (1). Предложенный способ достаточно прост и обеспечивает высокую точность и скорость определения параметров экранов. Найденные с его помощью данные о размерах одно-, двух- трехщелевых экранов подавления приведены на рис. 2. Данные представлены в виде серий кривых: каждая серия соответствует определенному числу щелей, а каждая кривая определяет в обобщенных параметрах υ j изменение высоты соответствующей кромки.

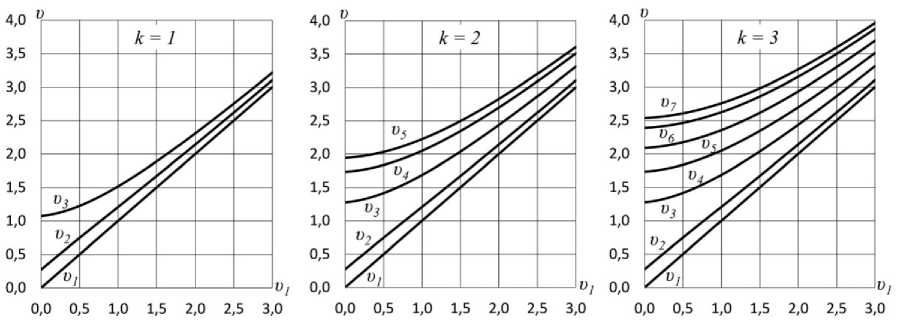
Рис. 2. Оптимальные параметры для щелевых экранов с различным числом щелей k

Из представленных на рис. 2 графиков видно, что при малых значениях υ все кривые (кроме первых двух υ₁ и υ₂) носят ярко выраженный нелинейный характер, однако с возрастанием значения υ они постепенно переходят в асимптотические прямые. Это, очевидно, объясняется тем, что при малых υ на условие определения оптимальных размеров накладываются два фактора: фазовое соотношение лучей от кромок и соотношение между их интенсивностями. При больших же значениях υ интенсивности лучей от кромок уравниваются и оптимальные высоты кромок экрана зависят только от фазовых соотношений, что приводит к квазилинейному ходу кривых. Представленными графиками можно пользоваться для определения распределения полосок и просветов в случае, когда произвольным образом задана высота нижней кромки υ₁ или общая высота υ_2k+1 всей экранирующей системы в указанных пределах. При больших значениях параметров υ приближенно можно считать постоянными ширины полосок и просветов (изменяется лишь параметр υ 1 , т.е. высота нижней кромки).

Из численных методов решения уравнения (1) ввиду ряда причин наиболее подходящим для нашего случая является итерационный метод Ньютона: а) функции непрерывны и легко вычисляемы вместе со своими производными, б) быстрая сходимость к решению, в) легко получить начальное приближение, исходя из решения графоаналитическим способом.

Практический интерес представляет также картина пространственного распределения дифракционного поля вблизи создаваемого абсолютного минимума поля. Пространственное распределение поля имеет значение для оценки величины допуска при выборе положения и размеров экранирующих систем, формирующих дифракционное поле, а также для сравнения и выявления наиболее эффективных вариантов в тех или иных конкретных ситуациях. Наиболее наглядную информацию о пространственном распределении дифракционного поля щелевых экранов дают линии постоянного уровня подавления в меридиональном сечении. Эти линии удобно строить относительно точки локального минимума поля (x 0 , 0, 0) в виде зависимостей Ф(q x , q z ) от некоторых безразмерных координат:

qx

x - x о -         z            z

; q == x 0          b (x 0)   V^m 0 (1 - m 0 )x 0

определяющих положение исследуемой точки относительно точки локального минимума (фокальной). Здесь x 1 /x 0 = m 0 – параметр, определяющий положение экрана относительно фокальной точки.

На рис. 3 представлены некоторые результаты расчетов, которые дают общую картину пространственного распределения дифракционного поля вблизи фокальных точек.

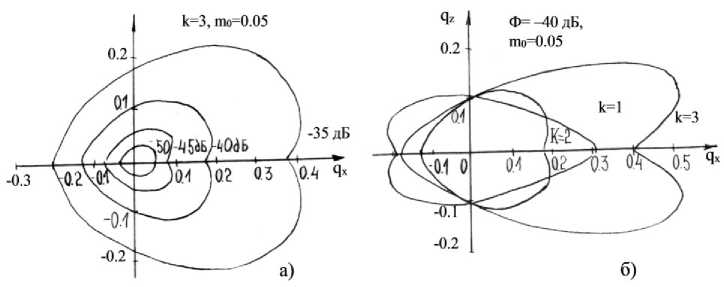
Рис. 3. Картина пространственного распределения дифракционного поля вблизи фокальных точек

Линии постоянного уровня подавления имеют для экранов с любым количеством щелей асимметрию относительно локального минимума поля (относительно фокальной точки q_x = 0, q_z = 0) по оси q_x. Наблюдаемая асимметрия постепенно исчезает с увеличением уровня подавления. Это хорошо видно в случае двухщелевого (k = 2) экрана (рис. 3а), где уже на уровне –50 дБ линию постоянного уровня можно считать симметричной относительно оси q z . Обращает на себя внимание форма линий постоянного подавления, имеющая с одной стороны седловидный, а с другой – выпуклый (заостренный) вид, причем в случае двух– и трехщелевых экранов седловидная часть обращена в сторону экрана (рис. 3б). Асимметричность линий равного подавления показывает, что на всех уровнях подавление обеспечивается в более широкой пространственной области справа от фокальной точки (в сторону удаления от экрана), нежели слева.

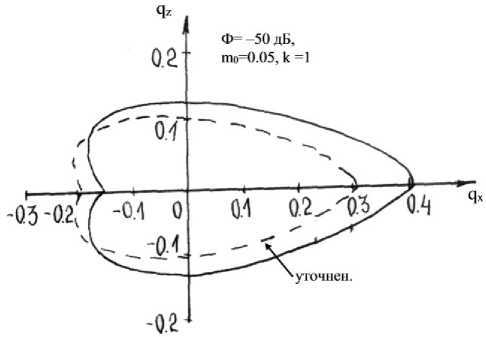
Рис. 4. Пространственные картины ослабления поля, полученные графоаналитическим способом и итерационным методом Ньютона

Представляет интерес сравнение пространственных размеров экранируемой области в зависимости от числа k щелей экрана. На рис. 3б приводится такое сравнение на уровне –40 дБ в случае расположения экранов в точке с относительной координатой m 0 = 0,05. Как видно, наиболее широкую область подавления в правой части от фокальной точки создает трехщелевой экран, однако в левой час-