Щелевые импульсные состояния и дисперсионный анализ механического поведения вязкоупругих сред

PNRPU MECHANICS BULLETIN

Определение вида дисперсионных соотношений является актуальной задачей для понимания и прогнозирования поведения и свойств неравновесных систем. Преобразование исходного волнового уравнения в дисперсионное соотношение является эффективной процедурой получения простой эквивалентной записи волнового уравнения. При таком преобразовании сохраняются фундаментальные свойства и связь характеристик волны, распространяющейся в нелинейной среде [1].

Анализ дисперсионных соотношений, как правило, даёт более ясное представление о поведении и физических свойствах систем с помощью таких характеристик, как групповая и фазовая скорость, энергетический спектр волны. Теория дисперсионных соотношений как инструмент исследования волновых процессов применяется в различных областях физики, таких как физика твердого тела [2–4], гидродинамика [5–8], электродинамика и оптика [9–11], квантовая механика [12; 13]. Наиболее простая форма зависимости частоты (энергии) от волнового числа (импульса) может быть получена с помощью линейных безразрывных дисперсионных соотношений. Дисперсионные соотношения данного класса описывают, например, распространение фотонов и фононов в кристаллических твердых телах, пренебрегая взаимодействием между частицами и дефектами кристаллической структуры. Для описания поведения реальных систем, как правило, используются нелинейные дисперсионные соотношения. В теории нелинейных волн появление нелинейных дисперсионных соотношений обусловлено влиянием таких факторов, как нелинейность свойств среды, диссипация энергии в системе, дисперсия групповых скоростей [14]. Физическая причина появления этих факторов определяется как нелинейным характером взаимодействия частиц среды с внешними полями, так и особенностями структуры среды (наличие дефектов и неоднородностей).

Особого внимания заслуживают нелинейные дисперсионные соотношения с разрывом по энергии (the energy gap) и разрывом в пространстве импульсов (the gap in momentum space). Резкое изменение скорости распространения частиц вблизи разрыва свидетельствует о качественном переходе механизма переноса импульса и распределения энергии в системе. Этот факт указывает на возможное появление принципиально новых свойств и эффектов в системе [3].

Феномен энергетической щели встречается в современных работах в рамках исследования структуры и физических свойств новых материалов, таких как наноматериалы, биоразлагаемые полимеры [15–18]. Работы включают исследования, посвященные как созданию математических моделей для объяснения этого явления, так и экспериментальные исследования, направленные на обнаружение энергетической щели в различных материалах. Понимание физических причин появления энергетической щели является важным фактором для управления этим феноменом при разработке материалов с уникальными свойствами.

Ко второму типу относятся дисперсионные соотношения с разрывом в пространстве импульсов [19–27]. «Щелевые состояния», обнаруживающиеся в процессе построения дисперсионных кривых данного класса, представляют собой интервалы волновых чисел с нулевыми значениями частот. Формирование «щелей» или разрывов дисперсионных соотношений имеет решающее значение для объяснения динамики коллективных мод различных систем, выделения характерных масштабов рассматриваемых процессов. Понимание природы и механизмов разрыва в пространстве импульсов позволит установить особые динамические и термодинамические свойства различных неравновесных систем [28].

В жидкостях эти механизмы связаны с коллективными сдвиговыми модами (возбуждениями) [19; 29–33]. Как известно, движение частиц в жидкости реализуется по двум сценариям: колебания в квазиравновесных положениях и диффузные скачки в соседние положения. Экспериментально установлено, что динамика колебаний частиц в жидкости при распространении продольных волн качественно идентична динамике, наблюдаемой в твёрдых телах [34]. Динамика поперечных (сдвиговых) колебаний жидкости проявляется в течение ограниченного времени и на ограниченных масштабах [30]. Отсутствие сдвиговой упругости на больших масштабах приводит к преобладанию механизма сдвиговой диффузии над механизмом распространения сдвиговых волн. В режиме сдвиговой диффузии происходит постепенное перераспределение частиц в жидкости, что препятствует существованию и устойчивому распространению поперечных волн. Однако на малых пространственных и временных масштабах жидкости демонстрируют сдвиговую упругость, характерную для твёрдых тел [35].

Для описания сдвиговой упругости в жидкостях уравнения классической гидродинамики необходимо модифицировать с использованием вязкоупругих моделей. В работах [19; 36] на основе моделей вязкоупругости Максвелла и Кельвина – Фойгта были получены волновые уравнения, характеризующие динамику сдвиговых мод в жидкостях. Анализ дисперсионных соотношений при использовании представленных моделей выявил разрыв в пространстве импульсов.

Актуальной задачей является применение других вязкоупругих моделей для исследования «щелевых состояний». Основная проблема существующих исследований [37–39] посвященных выводу дисперсионных соотношений на основе этих моделей, заключается в отсутствии исчерпывающего анализа полученных уравнений в контексте обнаружения разрыва в пространстве импульсов.

Настоящая работа сфокусирована на выводе и анализе дисперсионных соотношений, полученных с использованием вязкоупругих моделей Кельвина – Фойгта, Максвелла, стандартного линейного тела, модели Кельвина – Фойгта с дробной производной. Исследование разрыва в пространстве импульсов с учетом сдвиговой упругости в жидкостях позволит установить универсальные вязкоупругие свойства конденсированных сред. Поскольку интересующие эффекты, связанные с качественной сменой механизма переноса импульса, в жидкостях наблюдаются при взаимодействии сдвиговых мод, то в работе были рассмотрены уравнения только для поперечных (сдвиговых) волн. Алгоритм получения дисперсионных соотношений был основан на применении уравнения упругой поперечной волны в твёрдых телах и его модификаций для учета вязкости и диссипации. Таким образом, для каждой модели получены аналитические выражения дисперсионных уравнений и решения для них. Сформулированы критерии качественного изменения вида дисперсионных уравнений для обнаружения «щелевых состояний».

1.    Модель Кельвина – Фойгта

Рассмотрим особенности дисперсионных соотношений на примере моделей Максвелла и Кельвина – Фойгта, определяющих характерные случаи вязкоупругого поведения. Определяющее соотношение модели Кельвина – Фойгта имеет вид (рис. 1):

O = G I E + T_c

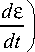
(1.1)

где σ – сдвиговое напряжение, ε – величина сдвига,

η

τ=    – время ретардации, G , η – модуль сдвига и ко-

G эффициент вязкости соответствующих элементов.

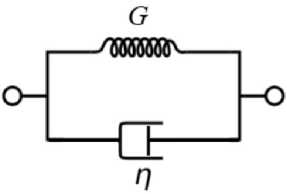
Рис. 1. Схема модели Кельвина – Фойгта

Fig. 1. Schematic representation of the Kelvin – Voigt model

Вывод дисперсионных соотношений связан с подстановкой оператора (1.1) в уравнение распространения упругих поперечных волн в твёрдых телах:

∂ ² v    ∂ ² v

G =ρ , ∂ x ² ∂ t ^2,

(1.2)

где v ‒ смещение частиц среды в плоскости, перпендикулярной направлению распространения волны (оси x ). Модификация выражения (1.2) предполагает замену линейной зависимости σ= G ε на зависимость

σ= M ε ,

M = G I 1 + т_п — I , I ° dt )

(1.3)

(1.4)

которая приводит к уравнению

∂ ² v         ∂ ³ v

^G ∂ x ^{2 + G} τ^σ∂ x ² ∂ t

_∂ 2 _v

=ρ .

∂ t ²

(1.5)

Представление решения v = v ₀ exp( i ( kx - ω t )) в виде плоской волны позволяет перейти от волнового уравнения (1.5) к дисперсионному соотношению вида:

На рис. 2 представлены решения (1.7) при параметрах G = 2 ⋅ 10⁶ Па, ρ = 1000 кг/м³ и различных значениях времен ретардации. Малые времена ретардации свидетельствуют о преобладании механизмов упругости над механизмами вязкости. Поэтому при малых временах ретардации отклонение графиков от прямой, характеризующей линейную зависимость частоты от волнового числа в идеально-упругих телах, происходит значительно позже.

2.    Модель Максвелла

В отличие от модели Кельвина – Фойгта, в структурной схеме модели Максвелла упругий и вязкий элемент расположены последовательно (рис. 3). Определяющее соотношение модели имеет вид:

ω ² +τ_σ c ² k ² i ω- c ² k ² = 0,            (1.6)

σ+τε

d σ

= G τ _ε dt

d ε dt ^,

(2.1)

где c= G/ ρ – скорость распространения упругой по- где σ – сдвиговое напряжение, ε – величина сдвига, перечной волны. Появление дисперсии в среде приводит к частотной (длинноволновой) зависимости скорости распространения волны c, что отражается на различии в значениях фазовой и групповой скорости (скорости волнового пакета) волны. Выражение (1.6) представляет собой квадратное уравнение относительно частоты ω . Ре-

η

τ=    – время релаксации, G , η – модуль сдвига и ко-

G

эффициент вязкости соответствующих элементов.

шение этого уравнения имеет вид:

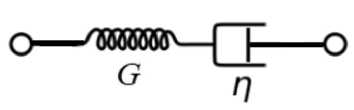
Рис. 3. Схема модели Максвелла

ω=

i ± ck 1 -

222 τ ck

(1.7)

Fig. 3. Schematic representation of the Maxwell model

Из (1.7) можно определить критическое значение волнового числа k_g , при котором образуется «щель» в k-пространстве:

c τ _σ

(1.8)

k g

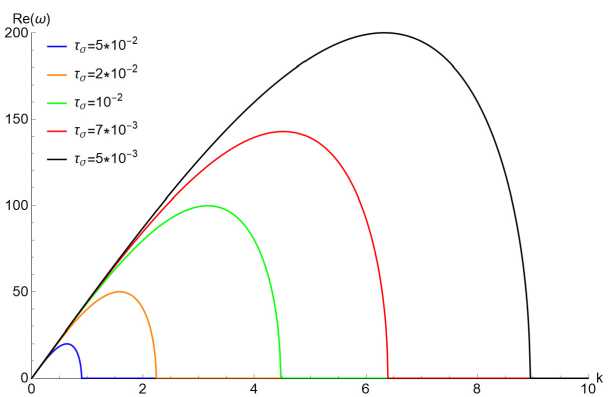
Рис. 2. График зависимости частоты от волнового числа при различных значениях времен ретардации для модели Кельвина – Фойгта

Fig. 2. Frequency-wavenumber dispersion curves for the Kelvin – Voigt model at various retardation times

Для получения дисперсионного соотношения и его дальнейшего анализа для модели Максвелла выполним действия, аналогичные преобразованиям для модели Кельвина – Фойгта. За основу принимается волновое уравнение распространения упругих поперечных волн в твёрдых телах (1.2). Для получения прямой зависимости (1.3) из уравнения (2.1) вводится вспомогательный опе- d     dB - 1

ратор B =1 +τ , откуда = и выражение (2.1) ε dt            dt τε принимает вид:

Bσ=G(B-1)ε,(2.2)

откуда

M=G(1-B-1 ).(2.3)

Выполним подстановку выражения (2.3) в уравнение

• (1 .2), заменив модуль сдвига G на оператор M :

G(1-B-1)∂2v=ρ∂2v.(2.4)

∂x2

Умножая обе части уравнения на оператор B , получим:

G ( B - 1 )	∂ 2 v 2 =ρ B ∂ x	∂ 2 v ∂ t 2,	(2.5)
G   ∂∂ 2 v ε ∂ t ∂ x 2	= P < 1 + T	1A d 2 v d t J d t 2 ,	(2.6)
∂ ∂ 2 c 2 τε ∂ t ∂ x	v ∂ 2 v ∂ 3 v 2 =∂ t 2 +τε∂ t 3,		(2.7)
∂ 2 v c 2 τ ε    2 ∂ x 2	∂ v =∂ t +τε	∂ 2 v ∂ t 2.	(2.8)

Принимая гипотезу плоской волны, определим вид волновой функции из уравнения (2.8) как v = v ₀ exp( i ( kx - ω t )) и получим дисперсионное соотношение вида [19]:

ω+ ⁱ ω- c ² k ² = 0.             (2.9)

τε

Решение уравнения (2.9) имеет вид:

• i1

3.    Модель стандартного линейного тела

ω=-   ± ck -    .         (2.10)

2 τ ε             4 τ ε

Действительные значения частоты принимают ненулевые значения только при волновых числах, больших критического значения k_g :

Для модели стандартного линейного тела определяющее соотношение имеет вид:

_ . d о < ( .   d E A

° ^+TCT = ^G o |^E+T»T I ^,         (3.1)

dt ^ dt J где σ – сдвиговое напряжение, ε – величина сдвига,

η                            (G1+ G0)

τ=    – время релаксации, τ=        η – время ре-

G 1                             G 1 G 0

тардации, G ₁, G ₀ – модули сдвига упругих элементов, η – коэффициент вязкости соответствующего элемента. Схема для модели стандартного линейного тела приведена на рис. 5.

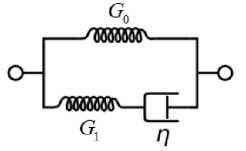
Рис. 5. Схема модели стандартного линейного тела

Fig. 5. Schematic representation of the standard linear solid model kg

2 c τ_ε ^.

(2.11)

Диапазон волновых чисел от 0 до k_g характеризует разрыв в пространстве импульсов.

На рис. 4 проиллюстрированы решения (2.10) при параметрах G = 2 ⋅ 10⁶ Па, ρ = 1000 кг/м³ и различных значениях времен релаксации. Ширина «щели» по оси k растёт по мере уменьшения времени релаксации.

Введем вспомогательный оператор B =1 +τ , от-ε dt dB-1

куда =      . Выражение (3.1) в таком случае примет

dt    τε вид:

B σ= G ₀

1 + ^i(B-1) IE, I TE       J

(3.2)

откуда

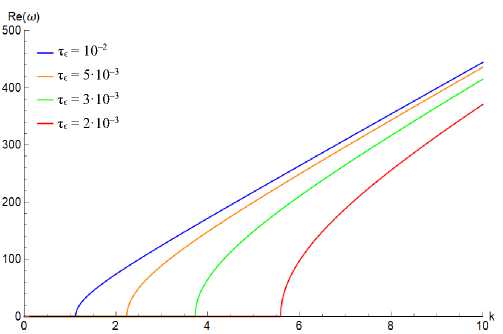
Рис. 4. График зависимости частоты от волнового числа при различных значениях времен релаксации для модели Максвелла

M=

G o 1 1 ■ ^ B - 1 )

I TE

B

(3.3)

Выполним подстановку выражения (3.3) в волновое уравнение (1.2):

Go (1+|( B-1) Idv = p B d2v, TE        J dx        dt

(3.4)

ε

f,      d A d² v Г     d A d² v

^G 0 I¹ ^ Ь =P I^{1 + T} E I , ^       d t J dx² ^       d t J d t²

(3.5)

Fig. 4. Frequency-wavenumber dispersion curves for the Maxwell model at various relaxation times

∂ ² v ∂ ³ v ∂ ² v ∂ ³ v G + G τ =ρ +ρτ . ⁰ ∂ x ^{20 σ}∂ x ² ∂ t     ∂ t ^{2 ε}∂ t ³

(3.6)

Получили достаточно сложный вид волнового уравнения (3.6). Принимая гипотезу плоской волны, перейдём к дисперсионному соотношению вида:

k2 =

p t„tEw4 + ю2 + iю3 (тя -te)

G 0         t „ w ² + 1

(3.7)

a ² - 3 b = P - 3 G ₀ к ² t , T_e

9             9 P t E ’

2 a ³ - 9 ab + 27 c = 2 P + 9 G 0 к ²T e ( 3 T e - t „ )

54                 54 P T 3

(3.13)

k = ±w

p ( ^T „ ^T e ® ^{2 + 1 +} i ^ю ( ^Т „ ^-Т е ) )

G O ( ^т„^ю2 ⁺ 1 )

(3.8)

S = Q ³ - R ²

G 0 к ² ( - 4 P 2 - 4 G 0 ² к ⁴ T „ T e + G 0 к ²P ( T „ + 18 T „ T e - 27 t E ) ) 108 P ³ t 4

Заметим, что при t „ = t_E , что можно допустить при G 1 <<  G₀ и n <<  G о , дисперсионное соотношение (3.8) преобразуется к виду:

Вид решения для z зависит от знаков параметров Q и S :

• при S > 0 получим три действительных корня

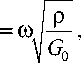
(3.9)

■ 1 = ^{- 2} 4q cos ( ф )^- 3,

■ 2,3 =^- 2 4Q cos ( ф± у 'j - a ,

ф

что в точности соответствует дисперсионному соотношению в идеально-упругих твердых телах [4].

Из дисперсионного соотношения (3.8) можно определить зависимость частоты и волнового числа, соответствующей структурно-механической модели Максвелла (рис. 2.1). Для этого примем значение мо-

= — arccos

R

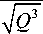
• при S <  0 и Q >  0 уравнение имеет два комплексных и один действительный корень

дуля сдвига G 0 равным 1 ^Т„^ТЕ^Ю 2 ^{+ 1 +} i ^Ю ( ^Т„^-Те ) G O        т „ ю ² + 1

тю+ i „ даст -£----. В результате

T_Ew G

(3.7) принимает вид:

нулю. Предел выражения из (3.8) при условии G0 ^ 0

дисперсионное соотношение

w² + w — - c² k ² = 0, ^T e

(3.10)

z1 =-2sgn (R) 7Q cosh (ф)-3, z 2,3 = sgn (R) TQ cosh (ф)-3 ± i V3 TQ sinh (ф),

ф = 3 Arccosh

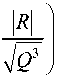
• при S <  0 и Q <  0 решение аналогичное

что в точности совпадает с уравнением (2.9).

Для вычисления аналитического решения уравнения (3.7) выполним преобразование этого уравнения:

± Ю² - AG М_и- ^к^ = 0.     (3.11)

^Te          P ^Te        P ^Te

Полученное кубическое уравнение (3.11) содержит мнимые коэффициенты. Приведём его к другому виду с помощью замены ю = iz :

z 1 =^- 2sgn ( R ) _X ^Q sinh ( ф ) ^- 3,

3 ± i v3 7 Q 1 cosh ( ф ) ,

z 2,3=sgn (R) TQi sinh (ф)- ф = — Arcsinh

R

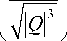
• при S <  0 и Q = 0 корни выглядят следующим образом

73+ 1 2 . к2Gо Ха     22G( z +--z +---z +--

T e          P T e P Т е

= 0.

(3.12)

z ₁

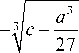
a

3,

Для решения кубического уравнения (3.12) с действительными коэффициентами воспользуемся тригонометрическими формулами Виета. Использование этих формул позволяет получить аналитическое решение с помощью тригонометрических функций в компактном виде. Для нахождения решения (3.12) выпишем действительные коэффициенты a = 2_, b = ^{к G 0} Io., c = ^{к G 0} ,

Te ’         P Te ’       PTe затем вычислим значения параметров:

^z 2,3 = ^- —у ± 2^|( а ^{- 3} z 1 )( а ^{+ z} 1 ) ^- 4 ^b |,

• при S = 0 получим два действительных корня, один из которых является корнем кратности 2

z, = - 2 3 R - a , 1₃

3a z 2,3   R1X 3-

Возвращаясь обратно к решению уравнения (3.11) с неизвестной ю = iz , заметим, что для получения действительных частот необходимо рассматривать мнимые корни относительно переменной z . В результате получим:

, ( S <  0 ) n ( Q >  0 ) ,

ю 2 =± 43^Q cosh ( ф ) , ф = 3 Arcsinh

R

, ( S <  0 ) n ( Q <  0 ) ,

и = ± 2 71 ( a - ³ p )( a ⁺ p )^{- 4} b l ^, p = ^- 3

c — 27 — a ^, ( S <  0 )^П( Q = 0 ) ^,

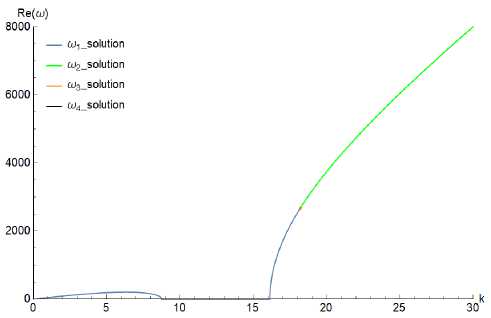
Рис. 6. Вид кусочно-заданной функции, состоящей из решений ю 1 , ю₂, ю₃, ю₄ в (3.14)

ю ₄ = 0, S >  0.

Подставляя готовые выражения вместо коэффициентов a , b , c , выпишем решения в окончательном виде:

, ( S <  0 ) n ( Q >  0 ) ,

Fig. 6. Form of the piecewise function composed of Ю 1 , ю₂, ю₃, ю₄ solutions as defined in (3.14)

ю ₂ =± 43 Ti Q cosh ( ф ), ф = 3Arcsinh

Г \

IRI

Q

, ( S <  0 ) n ( Q <  0 ) , ⁽³-¹⁴⁾

to; = ±--- 3₂

4 Q -I 2 R--Q

I т

, ( S <  0 ) n ( Q = 0 ) ,

ю ₄ = 0, S >  0.

На рис. 6 представлены решения и , ,ю₂,ю₃,ю₄ из (3.14) при параметрах G ₀ = 2 • 10 6 Па, р = 1000 кг/м³, т_а = 5 . 10 - ³ c, _{Т е} = 10 ^{- 4} с. Общее решение уравнения (3.11) представляет собой кусочно-заданную непрерывную функцию, состоящую из отдельных решений ю 1 ,ю₂,ю₃,ю₄ в (3.14). Из рис. 6 можно сделать несколько выводов.

Во-первых, последовательный переход от решения ю 1 к решениям ю₂ и ю₃ определяется условием Q <  0 или р - 3 g ₀ к ² _Тат_е<  0 . Очевидно, что при увеличении к значение параметра Q уменьшается и увеличивается вероятность этого перехода.

Во-вторых, появления решения ю₄ зависит от условия S > 0 или

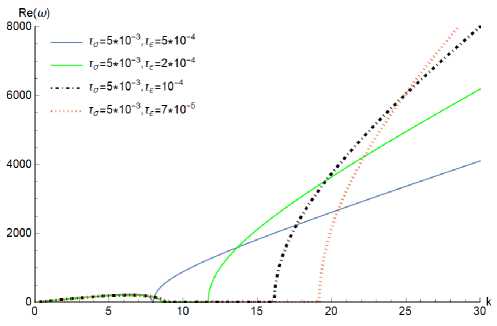
Рис. 7. График зависимости частоты от волнового числа при различных значениях времен релаксации для модели стандартного линейного тела

Fig. 7. Frequency-wavenumber dispersion curves for the standard linear solid model at various relaxation times

-4р2 -4G02к4т3 тЕ + G0к2р(т2 +18татЕ -27тЕ2) > 0. (3.15)

Решение ю₄ также определяет существование области с нулевыми значениями частоты (разрыв в k- пространстве). Условие (3.15) является критерием появления разрыва.

На рис. 7 и 8 представлены графики зависимости частоты от волнового числа при изменении времен релаксации тЕ и ретардации то . Анализ графиков показывает, что по мере сближения значений времен тЕ и то (тЕ < то) область нулевых значений частот (размер «щели») сначала уменьшается, а затем и вовсе исчезает (первый график на рис. 7, четвертый график на рис. 8).

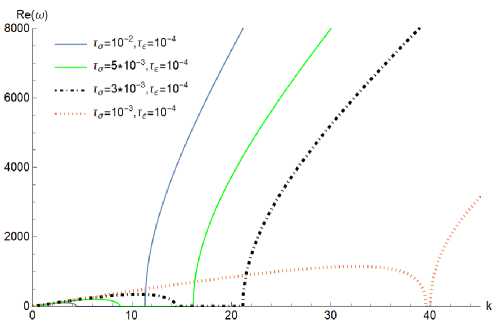
Рис. 8. График зависимости частоты от волнового числа при различных значениях времен ретардации для модели стандартного линейного тела

Fig. 8. Frequency-wavenumber dispersion curves for the standard linear solid model at various retardation times

4.    Дробные реологические модели

Дробные модели основаны на существенно новом представлении релаксационных функций (ядер релаксации), имеющих отношение к качественным изменениям реакции среды (жидкостей и твердых тел), термодинамических свойств, например, вида свободной энергии. При этом описание релаксационных свойств с использованием дробных моделей обусловлено нелинейной динамикой внутренних мезоскопических (структурных) переменных, «подчиняющих» релаксационные свойства макроскопических переменных (напряжения, деформации). «Дробная» феноменология на основе релаксационных моделей (моделей Максвелла, Фойгта) позволяет в ряде случаев успешно описать механическое поведение полимерных, композитных, биологических систем, обнаруживающих широкий спектр релаксационных механизмов в условиях «структурной перестройки» системы. При этом моделирование релаксационных механизмов достигается с относительно небольшим количеством параметров, характеризующих дробную пространственновременную кинетику и связанных с фундаментальными пространственными и временными масштабами, характеризующими эволюцию мезоскопических систем в условиях структурно-скейлинговых переходов [40]. Данные масштабы являются параметрами автомодельных решений, описывающими пространственно-временную динамику коллективных мод структурных мезоскопических переменных. Пространственные и временные масштабы определяют «дробный порядок» соответствующих производных в моделях вязкоупругого поведения сред. С учетом качественных изменений типов автомодельных решений эволюционных уравнений для мезоскопических переменных изменение «дробного порядка» в релаксационных уравнениях может иметь функциональный вид. Термодинамически это связано, как правило, с качественными изменениями неравновесных потенциалов (свободной энергии) и необходимостью введения «эффективных температур», определяющих изменение текущей «восприимчивости» системы в условиях внешних воздействий и обнаруживающих специфическое свойство «памяти» при релаксационной реакции твердых тел, жидкостей, а также эффектов теплопроводности.

Дробные вязкоупругие модели используют функцию памяти K ( s ) вида

K ( s ) = k^, ae ( 0,1 ) , k 0 >  0. (4.1)

Эксперименты по пластическому деформированию, ползучести для широкого класса материалов с затухающей памятью демонстрируют применимость техники дробных производных для описания изменения спектра времен релаксации при условиях нагружения, близких к квазистатическим [41].

Интерес представляет понимание природы степенного закона в механизмах релаксации, который наблюдается для широкого класса нелинейных систем, в том числе при пластическом течении в сплавах, когда проявляются многомасштабные коллективные эффекты локализации пластической деформации с выраженными макроскопическими признаками резкого изменения времен релаксации – флуктуациями напряжения пластического течения (эффект Портевена – Ле Шателье). Коллективное поведение областей локализованного сдвига характеризуется степенными распределениями флуктуаций напряжения пластического течения [42].

Появление многомасштабных коллективных мод сопровождается качественным изменением механизмов переноса импульса и диссипации, характерными для неравновесных «критических» систем. Степенные показатели при этом аналогичны показателям скейлинга в классической теории фазовых переходов. При характерных временах воздействия, близких к временам структурной релаксации (временам Френкеля), обнаруживаются «щелевые состояния – Gapped Momentum States», реализуемые на множестве волновых чисел (спектре масштабов). В зависимости от природы релаксационных механизмов (времена релаксации напряжений в модели Максвелла, времена ретардации деформаций в модели Кельвина или стандартного твердого тела) «щелевые состояния» определяют качественные изменения механизма переноса импульса, например, коллективные моды локализованного сдвига при пластическом течении, формирование вихрей в жидкости, зарождение и распространение коллективных ориентационных мод в полимерах, известные как эффект образования «шеек».

Взаимодействие множественных коллективных мод, локализованных на спектре «щелевых» масштабов, на макроскопических масштабах, например, на масштабе образца, приводит к резкому уменьшению времен релаксации (ретардации), что проявляется в выраженной степенной зависимости последних от параметров нагружения. Появление спектра «щелевых масштабов», соответствующего им спектра «временных масштабов Френкеля» и коллективных мод «структурных переменных» приводит к резкому изменению топологии фазового пространства, реализуемого в ходе множественного «распада» метастабильных состояний [43]. Спектр «щелевых масштабов» определяет пространственные (масштабы локализации коллективных мод) и их временные масштабы (масштабы Френкеля), на которых развивается релаксационная кинетика макроскопической системы. Взаимодействие между мезоскопическими масштабами на характерных макроскопических (пространственных и временных) масштабах может быть описана с использованием техники дробных производных. Ключевая роль пространственно-временных масштабов, определяющих динамику коллективных мод структурных (мезоскопических) переменных проявляется в ограниченности применения степенных законов изменения времен релаксации, определяющих физически нереальные значения модулей упругости в начальный момент времени. Устранение этого несоответствия достигается феноменологически введением временного масштаба tc, начиная с которого проявляются степенные закономерности в изменении времен релаксации. В [43] показано, что типичное значение этого временного масштаба tc соответствует временам Френкеля tc ⁓ tF ⁓ 10-5 с. Широкое распространение степенные реологические модели получили при описании свойств клеток с помощью введения двух параметров – жесткости (модуля) системы и показателя степени, определяющего меру близости к твердотельному или жидкоподобному состоянию. Важным аспектом является также то, что степенная модель была разработана не только на основе дробного исчисления, но и в рамках мезоскопической теории полимерных и биологических систем. Теория предполагает, что вырождение масштабов является естественным следствием метастабильности внутренней структуры материала, которая состоит из множества структурных элементов и соответствующих им энергетических минимумов, переходы между которыми определяются внешним воздействием и «эффективными температурами», изменения которых характеризуют переходы по множественному метастабильному потенциалу. Показатель степени при этом связан с эффективной температурой материала, которая задаёт динамику системы и устанавливает вероятность перехода элементов между энергетическими минимумами.

5. Дисперсионные свойства среды Кельвина – Фойгта с дробной производной

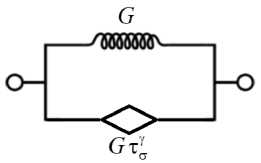
Рис. 9. Схема модели Кельвина – Фойгта с дробной производной

Fig. 9. Schematic representation of the fractional derivative Kelvin – Voigt model

Связь напряжений и деформаций в модели Кельвина – Фойгта с дробной производной определяется с помощью оператора

M = Go

( d И 1+т^ — |.

I    о dtYJ

(5.3)

При подстановке выражения (5.3) в волновое уравнение (1.2) получим:

d ² v

^G 0 л 2 ^{+ G} 0^т d x

Y о

d ^Y d ² v = d ² v dt ^Y d x ² P d t ²

(5.4)

Использование гипотезы плоской волны позволяет перейти к дисперсионному соотношению вида:

Структурная схема модели Кельвина – Фойгта с дробной производной состоит из упругого и вязкоупругого элемента, параллельно расположенных друг относительно друга (рис. 9). Определяющее соотношение модели имеет вид:

Y^- i « t

- G 0 k ² - G 0 т О k ² e « t d-e— = -p « 2 .      (5.5)

dt ^Y

Для вычисления дробной производной функции e ^-1« t воспользуемся формулой (5.2) и следствием из этой формулы [44]

о =Go е+т^— ,           (5.1)

dYf =   1    f(0) + r f '(т) dт

dtY   Г(1 -y)[ tY    J (t-т)7

(5.6)

где о - сдвиговое напряжение, е - величина сдвига,

П т = — - время ретардации, Go - мгновенный модуль G сдвига. Выражение d в (5.1) представляет собой dtY дробную производную Римана – Лиувилля

df = dt- d т, dtY dt J Г(1 -y)(t-т)7

(5.2)

где Y - порядок дробной производной (0 < у < 1 ), Г ( 1 - у ) - гамма-функция. При у= 0 вязкоупругий элемент в схеме становится идеально-упругим элементом, при Y = 1 данный элемент принимает вид идеально-вязкого элемента.

t - i сот e Обозначим Y( t ) = ----- -d т , тогда

00 (t-т)7

1      d y ( t )        1 Г 1 . _z 1

=              i W( t ) ,

Г(1 -y) dt     Г(1 -y) LtYJ dy(t) . z x 1

-IT ⁺ i ^w( t ) = 7 ’

y( t) = C[ e-«t - e - i«ti1+7 (-«)Y ГО-Y,- i«t),

« где Г(1 - y,-i«t) - неполная гамма-функция. Учитывая, что ^(0) = 0, получим

• - i«t 1+7Y

• V( t ) =--------(—^L ( Г(1 - Y ) - Г(1 - Y , - i « t ) ) . (5.8)

«

Выражение (5.8) представляет собой итоговое решение для функции ψ( t ) . При помощи этого решения вычислим дробную производную функции e ^{- i ω t} :

_d γ e - i ω t dt ^γ

d- ( dt ^ Г (1 -Y)

V( t ) I = e 't ( - i w ) ^Y| 1

Г ( —Y,— i w t ) ^

.

Г ( —Y ) )

В результате дисперсионное уравнение (5.5) принимает вид:

- G о k ² - G о t ^y k ² ( - i w ) ^YI 1 - ^r( _r Y’ i ^W t ) I = -p w ².      ⁽5.⁹⁾

I       r( -Y )    J

На рис. 10 построено численное решение дисперсионного уравнения (5.9) при различных значениях порядка дробной производной и параметрах G ₀ = 2 ⋅ 10 ⁶ Па, ρ = 1000 кг/м³, τ_σ = 5 ⋅ 10 ^{- 3} c, t =5⋅10 ^{- 3} с. При значениях параметра γ , близких к нулю, дисперсионное соотношение (5.5) сводится к уравнению, характерному для идеально-упругих твердых тел. При дальнейшем увеличении порядка дробной производной преобладают вязкие свойства среды. Наконец, при значениях параметра γ , близких к единице, модель преобразуется в классическую модель Кельвина – Фойгта. Это означает, что при данном условии результаты численного решения (чёрный график на рис. 10) практически совпадают с результатами на рис. 2.

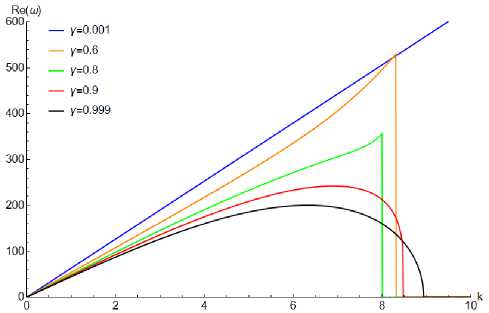
Рис. 10. График зависимости частоты от волнового числа при различных значениях порядка дробной производной для модели Кельвина – Фойгта с дробной производной

Fig. 10. Frequency-wavenumber dispersion curves for the fractional derivative Kelvin –Voigt model at various values of the fractional derivative order

Заключение

Настоящая работа посвящена выводу и анализу дисперсионных соотношений с использованием вязкоупругих моделей с целью исследования «щелевых состояний». Дисперсионные соотношения были получены в результате модификации уравнения упругой поперечной волны в твёрдых телах. Конечный вид модифицированных волновых уравнений определялся структурой выбранных вязкоупругих моделей. Переход между волновыми уравнениями и дисперсионными соотношениями осуществлялся с помощью гипотезы плоской волны в одномерном случае. В качестве вязкоупругих моделей были рассмотрены модели Кельвина – Фойгта, Максвелла, стандартного линейного тела, модель Кельвина – Фойгта с дробной производной. Сделаны выводы и сформулированы критерии качественного изменения вида дисперсионных уравнений для обнаружения разрыва в пространстве импульсов.

Несмотря на простоту и схожесть схем моделей Кельвина – Фойгта и Максвелла, эти модели описывают качественно различное вязкоупругое поведение среды. Как известно, при малых скоростях деформаций модель Кельвина – Фойгта описывает поведение материала, характерное для твердых тел, в то время как модель Максвелла при тех же условиях демонстрирует поведение вязкой жидкости [36]. Поэтому модель Кельвина – Фойгта хорошо предсказывает распространение звуковой волны с диффузионным затуханием, когда чисто упругий механизм при увеличении скорости деформаций постепенно сменяется вязким.

Как и в модели Кельвина – Фойгта, дисперсионное соотношение модели Максвелла содержит разрыв в пространстве импульсов, что подтверждается многочисленными исследованиями [19; 23; 29]. Наличие разрыва в дисперсионных кривых позволяет модели Максвелла описать динамику сдвиговых мод в жидкостях, когда сдвиговая упругость жидкости проявляется на ограниченных масштабах системы [19; 31]. Критическое значение волнового числа k_g , определяющее длину разрыва в пространстве импульсов, имеет обратную зависимость от двух параметров модели: скорости распространения упругой волны c и времени релаксации системы τ_ε .

Конечный вид дисперсионного соотношения, полученного из модели стандартного линейного тела, представляет собой кубическое уравнение относительно частоты и совпадает с уравнением из статьи [38]. Аналитическое решение этого уравнения было получено с помощью тригонометрических формул Виета. При обнулении модуля сдвига одного из упругих элементов дисперсионное соотношение модели преобразуется в дисперсионное уравнение модели Максвелла, что подтверждает адекватность полученного решения. Построенные дисперсионные кривые модели демонстрируют конечный разрыв в пространстве импульсов при определённых условиях. Для описания этих условий сформулирован критерий, включающий параметры модели и обнаруживающий «щелевые состояния» в системе.

Дисперсионное соотношение модели Кельвина – Фойгта с дробной производной, как и дисперсионное уравнение классической модели Кельвина – Фойгта, содержит разрыв в пространстве импульсов. В случае, когда параметр дробной производной стремится к единице, что соответствует преобразованию вязкоупругого элемента в вязкий элемент, результаты модели сводятся к результатам классической модели Кельвина – Фойгта. При стремлении параметра дробной производной к нулю схема модели состоит из двух упругих элементов, поэтому дисперсионные кривые представляют собой линейные функции.

Необходимость исследования «щелевых состояний» при анализе дисперсионных соотношений обусловлена появлением качественного нового механизма переноса