Широтно-импульсное управление электрореактивными двигателями при коррекции орбитального движения спутника
Автор: Сомов Сергей Евгеньевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 6-3 т.17, 2015 года.
Бесплатный доступ
Представляется метод удержания малого спутника землеобзора на солнечно-синхронной орбите по долготе восходящего узла. Созданы алгоритмы широтно-импульсного управления КДУ с 8 электрореактивными двигателями и приведены результаты исследования разработанных алгоритмов.
Коррекция орбитального движения спутника, электрореактивный двигатель
Короткий адрес: https://sciup.org/148204326
IDR: 148204326 | УДК: 629.78
Текст научной статьи Широтно-импульсное управление электрореактивными двигателями при коррекции орбитального движения спутника
Разнообразные возмущающие факторы обуславливают отличие реального траекторного движения информационного спутника (связи, геодезии, землеобзора и др.) от его расчетного движения. Если такое отличие превосходит допустимые отклонения, то возникает необходимость коррекции (исправления) характеристик орбитального движения спутника на основе результатов наземных и космических (ГЛОНАСС/GPS) измерений параметров его фактической орбиты.
При постановке задачи орбитальной коррекции с помощью традиционных реактивных двигателей большой тяги обычно принимают допущение об импульсном характере изменения вектора скорости v ( t ) в некоторой точке движения спутника. Текущее состояние спутника на орбите определяется 6 общеизвестными параметрами кеплерова орбитального движения либо 6 фазовыми координатами – 3 компонентами вектора положения r ( t ) = {r z .( t ) i = 1 ^ 3} и 3 компонентами вектора скорости v ( t ) = {v z ( t )} поступательного движения спутника в околоземном пространстве. Для выполнения полной коррекции необходимо 6-ти параметрическое (по числу корректируемых параметров) управляющее воздействие. Однако в случае импульсного характера коррекции управляющими воздействиями могут быть только три компонента вектора скорости v ( t ) . Следовательно, для исправления всех шести параметров орбитального движения спутника требуется как минимум два включения корректирующей двигательной установки (КДУ) на основе реактивных двигателей для выполнения 2 трехкомпонентных коррекций. Реализация таких
Сергей Евгеньевич Сомов, научный сотрудник отдела «Динамика и управление движением».
коррекций наиболее сложна и требует высокоточной ориентации оси действия тяги КДУ в системе координат, в которой вычислялось направление потребного корректирующего импульса этой тяги. Требования к точности ориентации оси действия тяги КДУ значительно ослабляются при выполнении двухкомпонентных и однокомпонентных орбитальных коррекций.
При баллистических расчетах обычно предполагается, что суммарный вектор тяги КДУ проходит через центр масс (ЦМ) спутника C , и решаются задачи оптимизации траекторного движения по существу лишь одной точки C по расходу топлива, энергетическим, временным и др. критериям. Между тем, если принять конструкцию спутника в виде твердого тела со связанной системой координат (ССК) O xyz с началом в фиксированной точке конструкции - полюсе O , то при стандартных обозначениях модель динамики его пространственного движения в ССК имеет вид [1]
m v o - L x ci) - го x (L x m) = R o,
Lxv o + K +mxK = M o , где vo = vo + to x vo, L = mpc - вектор статического момента, K = Jo - вектор кинетического момента (КМ), постоянный вектор pc представляет расположение ЦМ C в ССК, а Ro и Mo - главные векторы внешних сил и моментов, представленные в ССК. В проектном (расчетном) варианте точки C и O совпадают, тогда вектор pc ^ 0, что дает L = 0, уравнение углового движения отделяется, но в уравнении поступательного движения остается зависимость от скорости вращения ССК m в инерциальной системе координат (ИСК). При совпадении точек C и O векторные уравнения поступательного и вращательного движений спутника полностью разделяются только при их представлении в ИСК в виде m v0 = R0; K 0 = M 0, где верхним индексом I отмечено, что указанные векторы определяются их проекциями на оси ИСК. В процессе орбитального полета спутника в силу ряда причин (расход топлива, изменение конфигурации навесных конструктивных элементов, например панелей солнечных батарей (СБ), и др.) вектор pc ^ 0, поэтому поступательное и вращательное движения спутника являются связанными.
Векторы внешних возмущающих сил и моментов, действующих на спутник, физически формируются в отношении его ЦМ C , этот факт следует учитывать при расчете главных векторов внешних возмущающих сил и моментов в полюсе O . С другой стороны, в силу технологических условий установки реактивных двигателей на корпусе космического аппарата (КА) ось действия суммарной тяги КДУ не проходит точно через полюс O и при коррекции орбитального движения спутника возникает возмущающий момент КДУ. При этом система управления ориентацией обеспечивает стабилизацию требуемого углового движения спутника и в ее электромеханических исполнительных органах (ЭМИО) с вектором КМ H происходит накопление вектора суммарного КМ G = K + H механической системы, обусловленного внешним возмущающим моментом.
Для эпизодической разгрузки ЭМИО от накопленного КМ традиционно применяется магнитный привод (МП), который создает механический момент за счет взаимодействия его электромагнитного момента с магнитным полем Земли. Однако здесь имеются общеизвестные ограничения [2,3] на доступные значения модуля и орта направления вектора механического момента МП, поэтому в [4] впервые предложено выполнять разгрузку ЭМИО при одновременном широтно-импульсном управлении как МП, так и КДУ. Одновременное создание внешних сил и моментов с помощью электрореактивных двигателей (ЭРД) является актуальной проблемой управления движением информационных спутников [5] – [9].
Некоторые вопросы оптимального удержания КА на солнечно-синхронной орбите (ССО) при стандартных способах управления шестью ЭРД были исследованы в [10]. При использовании ССО скорость прецессии плоскости этой орбиты равна средней угловой скорости годового движения Земли вокруг Солнца, при этом спутник землеобзора приблизительно в одинаковое солнечное время перемещается над фиксированной широтой земной поверхности. При решении задач космического землеобзора необходимо обеспечить [11,12] синхронность прецессии орбитальной плоскости ССО со средним движением Земли вокруг Солнца, стабильность высоты полета и местного солнечного времени на одной и той же широте, а также повторяемость прохож- дения трассы спутника через смежные районы съемки для полного покрытия заданного района земной поверхности. В статье решается задача разработки алгоритмов широтно-импульсного управления 8 ЭРД в составе КДУ оригинальной схемы [13] при удержании малого спутника зем-леобзора на ССО.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
В дополнение к ИСК и ССК стандартным образом вводятся орбитальная система координат (ОСК) и геодезическая гринвичская система координат (ГСК). Ориентация ССК относительно ИСК определяется матрицей направляющих косинусов C , а относительно ОСК Oxoyozo – углами крена ф1 = у, рыскания ф2 = ^ и тангажа ф3 = О. Для простоты предполагается совпадение положений ЦМ C и полюса O в ССК. В процессе полета КА изменяются все шесть элементов его орбиты - долготы восходящего узла (ДВУ) Q , наклонения i , фокального параметра p , экс- центриситета e , углового расстояния перигея мп и момента времени тп его прохождения спутником. В соответствии с общеизвестными законами механики космического полета [14] – [16] значения этих элементов орбиты варьируются под воздействием гравитационного поля Земли и сопротивления ее атмосферы, гравитационных полей Солнца и Луны, сил светового давления Солнца, а также управляющих и возмущающих воздействий КДУ на основе ЭРД.
На рис. 1 представлена схема КДУ на основе восьми ЭРД [13]. Здесь орты ep, p = 1 ^8, осей сопел 8 ЭРД имеют в ССК представления в виде столбцов с с а в
С с ав e1
- e 8
e 2
e 3
;
;
^^^^^^^в
C а S в
C а S в
S а
S а
- e 7
- e 6
|
C “ C " |
" C а C в |
|
|
- C а S , |
; e 4 e 5 |
- C а S в |
|
S а |
- S а |
,
где Sx = sin x , Cx = cos x , x = а е, P e .
Пусть p p является вектором точки O p приложения вектора тяги p -го ЭРД , причем в ССК векторы p p , p = 1 ^ 8 , представляются столбцами
|
[ b x 1 |
Г b x 1 |
Г b x 1 |
" b x |
||||
|
P 1 = |
b> |
; p 2 |
b , |
; p 3 |
- b, |
; p 4 |
- b y |
|
. b z . |
- b. |
. b . |
- b z |
р5 =
- b x b y bz
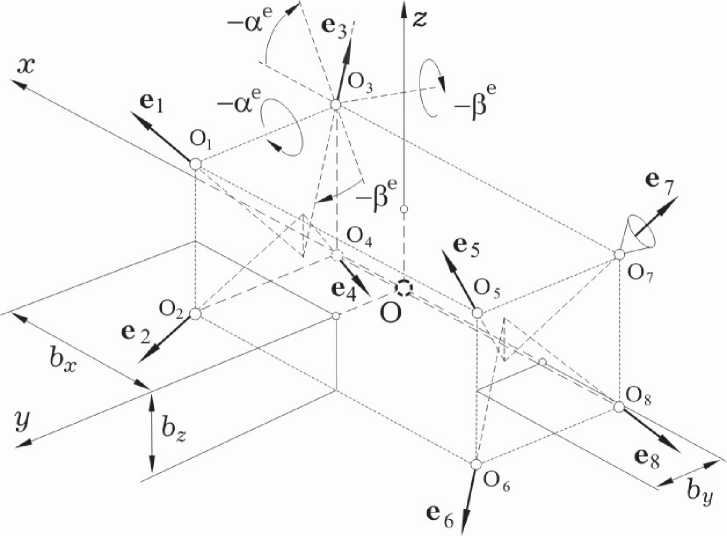
Рис. 1. Схема КДУ на основе 8 ЭРД
; Р б =
- b x b y - b z
; р 7
^^^^^^^^
^^^^^^^в
bx b y
b z
^^^^^^^е
; р 8
^^^^^^^в
^^^^^^^в
bx b y b z
.
Пусть также каждый ЭРД имеет широтноимпульсную модуляцию (ШИМ) тяги, что описывается нелинейными непрерывно-дискретными соотношениями pp(t) = Pm PWM(t-TeA,Tm, vpr) Vt e [tr,trJ с периодом Tue и временным запаздыванием Tzeu [17]. Здесь
PWM( t,t r , T m ,v pr ) ^
Signv pr t e [ t r ,t r + T pr ) ; 0 t e [ t r + T pr , t r + 1 )’
T = s
pr
0 sat( Tu e,|v pr
|)
t r = rT U , t r + 1 = t r + T U
|v pr | < T m
|v pr | > T m '
; r e N o = [0,1,2,3...) ,
где Pm
–
номинальное значение тяги, одина-
ковое для всех ЭРД в составе КДУ. В ССК вектор тяги p -го ЭРД вычисляется по формуле P p ( t ) = - p p ( t ) e p , а векторы силы R e и момента M e КДУ - по соотношениям R e = Z P p ( t ) и M e = Z [ p p x ] P p ( t ) .
ПОСТАНОВКА ЗАДАЧИ
Рассматривается задача удержания малого спутника землеобзора на круговой ССО за счет эпизодической коррекции его траекторного движения с помощью КДУ на основе 8 ЭРД . Пусть такой спутник массой m = 1000 кг движется
на высоте H = 600 км по ССО с наклонением i = 97.8 град. Для условной даты 22.01.2015 и времени прохождения восходящего узла 08:00:00 по Гринвичу над земной поверхностью с геодезической долготой Lп = 90 град (ДВУ Q = 331.36 град) драконический период обращения спутника T = 5801.23 с = 96.68 мин, что дает 14.89 витков в сутки.
Пусть КА оснащен 2 панелями СБ суммарной площади 50 м2 и нормаль к их рабочей плоскости наиболее близка к направлению на Солнце за счет регулярного одноосного вращения панелей относительно корпуса КА. Примем также, что коэффициент лобового сопротивления c x = 2.5 и при выполнении коррекции орбиты КА имеет фиксированную ориентацию в ОСК: углы крена Y = -10 град, рыскания ^ = 3 град и тангажа 0 = 8 град.
Солнце находится с одной стороны плоскости ССО – угол между направлением на Солнце и плоскостью орбиты равен - 28.11 град, силы аэродинамического сопротивления при указанной фиксированной ориентации ССК в ОСК и вращающихся крупногабаритных панелях СБ имеют несимметричный характер. В силу такой несимметричности притяжение Солнца и давление солнечного излучения приводит к вариациям положения орбитальной плоскости ССО (наклонение i и ДВУ ^ ), а силы аэродинамического сопротивления монотонно изменяют форму этой орбиты (фокальный параметр и эксцентриситет).
Приближенных аналитических соотношений [16], воспроизведенных в [10], недостаточно для достоверной среднесрочной (до 15 суток) оценки возмущений наклонения и ДВУ ССО с учетом
влияния сил солнечного давления и сил аэродинамического сопротивления при вращающихся крупногабаритных панелях СБ. Поэтому было выполнено численное исследование влияния всех внешних возмущающих сил (без включения КДУ) для рассматриваемого малого спутника на ССО с указанными параметрами. При этом влияние гравитационного поля Земли учитывалось 8 компонентами аналитического представления его потенциальной функции. Результаты такого анализа в отношении вариаций ДВУ 8Q и наклонения 5 i на трёх витках полета КА представлены на рис. 2.
Для используемых данных КА и ССО наибольшее влияние оказывают сопротивление земной атмосферы, гравитация Солнца и силы солнечного давления. При этом суточное изменение радиус-вектора ССО равно 13.5 м, за 10 суток полета уменьшение высоты орбиты составит более 100 м. Удержание КА на ССО может быть достигнуто только за счет эпизодической коррекции траектории спутника, в рассматриваемом случае с помощью КДУ на основе ЭРД. В отличие от КДУ с реактивными двигателями большой тяги, здесь коррекция орбитальных параметров выполняется на длительных временных интервалах и поэтому возможно аналитическое определение корректирующих силовых воздействий при различных составах корректируемых параметров орбиты [15, раздел 11.7]. При этом в ССК определяется вектор-функция R p ( t ) потребного импульса (pulse) вектора корректирующей силы t
Rp (t) = C( t )J C ‘(t) R е(т) dт, t0
которая должна быть реализована КДУ на основе ЭРД. Естественно возникает вопрос: каким же образом можно создать вектор потребного импульса корректирующей тяги Rp (t) произвольного направления в ССК, если орты ep осей сопел ЭРД фиксированы в ССК и каждый ЭРД может находится только в двух состояниях – включен (тяга pp (t) = Pm) либо выключен (тяга pp (t) = 0) ? Для решения этой проблемы применяется широтно-импульсная модуляция тяги всех 8 ЭРД, которая обеспечивает выполнение заданного значения вектора Rp (t) в моменты времени t = tr = r TU .
Для схемы КДУ на рис. 1 орты rp векторов pp вычисляются как rp =pp/р, где скаляр p = (bX + by + b2)1/2 является единым модулем точек O p приложения векторов тяги ЭРД в ССК. При обозначениях тr = {тpr}; De = {[ep],[rp X ep]};
r p = R p /Pm ; m p = M p /(Pm p ) ;
tp = {r p, m p }, где векторы Rp и Mp представляют импульсы векторов сил Re = R = {Rx,Ry,Rz} и моментов Me = M = {Mx,My,Mz} КДУ, заданные в ССК, принципиальная проблема заключается в решении векторно-матричного уравнения
D e т r = t p , т r e R + 8 , t p e R 6 ; (1)
при условии о относительно компонентов вектора-столбца тr= {tpr}, когда прямоугольная матрица Deи вектор-столбец tp e R6заданы. Ставятся задачи синтеза алгоритма управления КДУ на основе 8 ЭРД с ШИМ тяги (1), (2) 0 2000 4000 6000 8000 10000 12000 14000 16000 t,S Рис. 2. Вариации долготы восходящего узла и наклонения ССО на трёх витках полета и апробации этого алгоритма при выполнении коррекции ССО в отношении ДВУ. АЛГОРИТМ УПРАВЛЕНИЯ КДУ При использовании псевдообратной матрицы (De)# = (De^D^D^t)-1разработанный закон распределения длительностей тpr тяги всех 8 эрд в составе КДУ на каждом полуинтервале времени t е [tr, tr+1) ШИМ управления с периодом TU при указанных условиях имеет следующую простую алгоритмическую форму: т — (т e # pg ■ ~ —" Т Т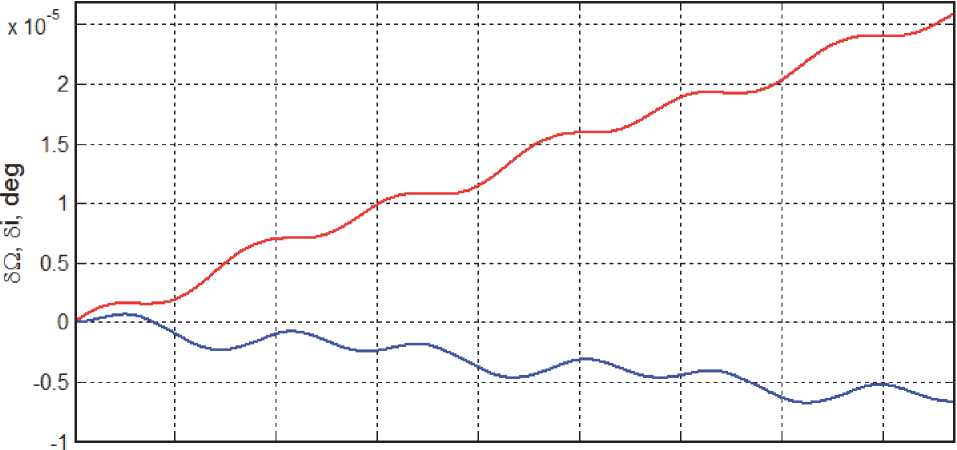
Список литературы Широтно-импульсное управление электрореактивными двигателями при коррекции орбитального движения спутника
- Лурье А.И. Аналитическая механика. М.: Физматлит, 1961.
- Коваленко А.П. Магнитные системы управления космическими летательными аппаратами. М.: Машиностроение, 1975.
- Алпатов А.П., Драновский В.И., Салтыков Ю.Д., Хорошилов В.С. Динамика космических аппаратов с магнитными системами управления. М.: Машиностроение, 1978.
- Сомов С.Е. Экономичное широтно-импульсное управление при разгрузке силового гирокомплекса системы ориентации мини-спутника//Проблемы управления. 2014. № 4. С. 60-68.
- Хоулдвэй Р. Использование двигателей малой тяги для коррекций орбиты и для управления положением спутников//Навигация. Наведение и оптимизация управления. Труды 7 международного симпозиума ИФАК по автоматическому управлению в пространстве. Том 3. М.: Наука, 1978. С. 14 -22.
- Rayburn C.D., Campbell M.E., Mattick A.T. Pulsed plasma thruster system for microsatellites//Journal of Spacecraft and Rockets. 2005. Vol. 42. No. 1. P. 161-170.
- Garulli A., Giannitrapani A., Leomanni M., Scortecci F. Autonomous low-Earth-orbit station-keeping with electric propulsion//Journal of Guidance Control and Dynamics. 2011. Vol. 34. No. 6: P. 1683 -1693.
- Платонов В.Н. Одновременное управление движением центра масс и вокруг центра масс при маневрах космических аппаратов на геостационарной и высокоэллиптических орбитах с использованием электрореактивных двигателей//Космическая техника и технологии. 2013. №1. С. 56-65.
- Nakajima Y., Murakami N., Ohtani T., Nakamura Y., Hirako K., Inoue K. SDS-4 attitude control system: in-flight results of three axis attitude control for small satellites//Proceedings of 19th IFAC Symposium on Automatic Control in Aerospace. 2013. P. 283-288.
- Ван Лицзе, Баранов А.А. Оптимальное удержание космического аппарата с двигателями малой тяги на солнечно-синхронной орбите//Вестник МГТУ им. Н.Э. Баумана. Сер. «Машиностроение». 2015. № 2. С. 68-82.
- Чернов А.А., Чернявский Г.M. Орбиты спутников дистанционного зондирования Земли: Лекции и упражнения. М.: Радио и связь, 2004.
- Vallado D.A. Fundamentals of astrodynamics and applications. Microcosm Press, Hawthorne and Springer, New York. 2007.
- Давыдов А.А., Игнатов А.И., Сазонов В.В. Применение реактивных двигателей для управления поступательным движением КА одновременно с разгрузкой кинетического момента электромеханических исполнительных органов//Препринты ИПМат РАН. 2006, № 082.
- Тихонравов М.К., Бажинов И.К., Гурко О.В. и др. Основы теории полета и элементы проектирования искусственных спутников Земли. М.: Машиностроение, 1974.
- Иванов Н.М., Лысенко Л.Н. Баллистика и навигация космических аппаратов. М.: Дрофа, 2004.
- Chobotov V.A. Orbital Mechanics. AIAA education series, 3rd edition, 2002.
- Somov Ye.I., Butyrin S., Somov S. Economical attitude and orbit control of information satellites by electromechanical, magnetic and plasma drivers//Proceedings of 6th IEEE/AIAA International Conference on Recent Advances in Space Technologies. 2013. P. 1009 -1014.
- Суханов А.А. Астродинамика. Сер. Механика, управление, информатика. М.: Изд-во Института космических исследований РАН. 2010.
- Ходненко В.П., Хромов А.В. Выбор проектных параметров системы коррекции орбиты космического аппарата дистанционного зондирования Земли//Вопросы электромеханики. Труды ВНИИЭМ. М.: 2011. Том 121. № 11. С. 15 -22.
- Somov Ye.I., Butyrin S., Somov S. Digital and pulse-width attitude control of land-survey mini-satellite//Proceedings of 22 Saint Petersburg International Conference on Integrated Navigation Systems. Saint Petersburg. 2015. P. 110-115.


