Шкив регулируемого диаметра для бесступенчатого вариатора

Предлагаемый шкив содержит несколько пар двуплечих рычагов 4 и 5, равномерно размещенных вокруг вала I и создающих рабочую поверхность 6, охваченную гибкой связью г?. Рычаги соединены друг с другом шарниром 8, а со ступицами 2 и 3 - шарниром 9. Увеличение диаметра шкива производится перемещением ступиц 2 и 3 навстречу друг другу, а уменьшение диаметра - их перемещением в противоположные стороны. Вс избежание чрезмерного натяжения гибкой связи шкивами лЛо.. Дорот, иэ проскальзывания по рабочий поверхностям в i4 изви пъ изменение диаметров взаимодействующих шкивов необходимо сиптронио.

На рис Л изображен шкив с положением рычагов, создающих минимальный диаметр, а на рис.2 - шкив при максимальном диаметре.

Как видно из чертежей, диапазон регулирования диаметра каждого шкива и, соответственно» передаточного отношения вариатора определяется только соотношением плеч рычагов 4 и 5 и общим габаритом устройства. поэтову представляется целесообразным ввести понятие ''ксзффициент изменения диаметра шютва к *’, равный отношению максимального диаметра шкива Д. к минимальному Д,п,т:

а также коэффициент, характеризующий передаточного отношения вариатора 1^, коэффициентов изменения дааметра шкивов:

диапазон изменения равный произведение

j lB Ш1 ' Ш2

Очевидно, что пр,:, перемещении ступиц в любом направление угол между рычагами 4 и 5 будет изменяться с предельное изменение - от 180° при горизонтальном положении рычагов, создающих минимальный .диаметр шкива, до 0°, когда ступицы полност но сдвинуты друг с другом и рычаги, стоя перпендикулярно к валу, создают максимальный диаметр, Соответственно, будет изменяться угол между верхними плечами рычагов.

Рис Л

Рис. 2

Передача вращающего момента

м вр

с

осуществляется с помощью клиноременной

одного шкива на другой гибкой связи ?. Сечение

такой ; такой связи представляет собой равнобочную трапецию с цш.з? средней линии а& и углом наклона ^ боковой стороны к оси Симметрии.

Обеспечить сцепление такой гибкой связи с рабочими гтазерхностями можно только в том случае, если при каждом измтаеьиз положения рычагов отноаггельно вала на рабочей псьгрлнссти будет точка, находящаяся на расстоянии а от оси т-шиетрии трапеции (сечения гибкой связи), при этом касательная, г.зоь денная к рабочей поверхности через эту точку, будет тред онить к оси симметрии под утлом «.

^ атле тичес кий р асчет формы рабочи х п оверхностей

Останин гибкой связи 7 (клиновидного ремня) представляет табод равнобочную трапецию со средней линией а» и острым углом та образуемым боковой стороной с осью симметрии трапеции. Нтасгходамо придать рабочим поверхностям 6 такую форму, чтобы они «.та таись (в математическом татад?) гибкой связи 7 при любом положении рычагов 4 и 5„ Ото < ття к следующей задаче.

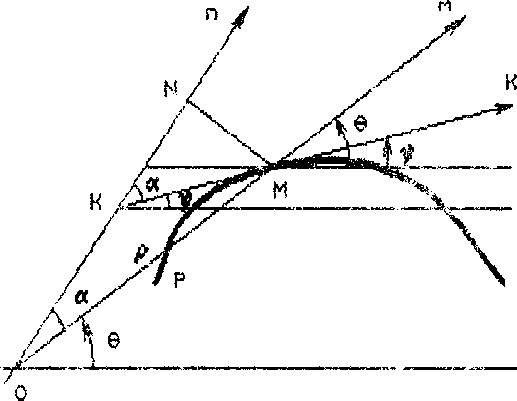
В татрной системе координат полюсом о найти кривую, обладающую свойством: в каждой точке м кривой касательная (.оставляет угол « с осью on, проходящей нз расстоянии а о*" гички и (рис. 3},

Заметим, что в предельно*! случае, когда ата. „та кривая тать не что иное, как логарифмическая опирал^.

Введем некоторые обозначения и попутно утончим постановку . ■ = in. Пусть ох - полярная ось, а - полярный угол точки г- ом - ее полярный радиус, от - луч, прохс.цящий через точку м, Из услогия задачи следует, что р>а (иначе но существует оси эп на расстоянии а от ТОЧКИ м).

Исходя из практического применения искомой кривой как продольного сечения рабочей поверхности рычага 4 (полярную ось о.-< считаем параллельной ваду I), из двух осей, проходящих через псл1)с о (в качестве полюса о принята ост шарнира 8) на расстоянии а от1 точки м, возьмем в качестве on ту ось, которая относительно луча от повернута против часовой стрелки. Пусть у -угол между on и №. Очевидно, о< у < п/г, причем у=п/й при ₽=а, о. когда точка м занимает положение точки в (рис. 3).

Далее,, из двух прямых, проходящих через точку м и составляющих данный угол асо<а<п/г) с осью on, будем считать касательной к искомо^ кривой ту прямую, которая повернута (ня угол а) относительно оси о- по часовой стрелке. Выберем на касательной прямой направление от точки к ее пересечения с осью on к точке м. Касательный луч м_к (рис.З) будем считать направленным в этом направлении.

х

Рис.З

^сознании через у угол наклона касательного луча н к полярной оси ох и положим ю=у-е. т.е. ^ - это угол наклона луча м_к к лучу см. т.к. е^^а, то г=^а. Отсюда следует, ч^п -а< to

Приступит*, к выводу уравнения кривой. Из прямоугольного треугольника omn жеем «sin, а, т.е.

р si nC ш -> cD = а ,                     Г 1 С

Раскрывая sinew + «о и заменяй sin® на ±ci+ctg^lw. (исключив тем самым на время ^=о), получи*

pCct-gw si net + cosoD ~ ±C3.*ctg u£ .

Как известно, для кривой с уравнением р=рсео справедлива ctgo = р’/р.

Подставляя это выражение в (2), получим дифференциальное уравнение искомой кривой pCpcosct * р* < :Р = ±а"Vp*' +р’ 2 .

Сделав замену р^', получим е (.costs а’^хшхЗ ™ lavl

ИДИ                               _ ау'Г-ю’ 2

о = In ------------------------ .                  С 32> jcosa + o' si isc* |

Дифференциальное уравнение (з), разрешенное относигельно искгиоэ функции о = с<ю, решаем известным приемом, а именно, ввода параметр р=о’, т.е.

о = Ina + 1 п"/С+р2 - In jcosa + psi na j , и продифференцировав это равенство по е, получим

_ Г Р _s 1 па) dp

4 1 +р cosa -t- psi па

ИЛИ

... f i                sina        1 , ati      .—- - -----------dp.

*■ 3. +р pCcosa + psi па) '

Заменим параметр р на «. Т.к. »=inp, то p-о* =р*/р=сх.ди>.

Поэтому f . sina ), cosnsinCto+a)^

ИЛИ de

Отсюда

. . f cosCto+oO ^yal sintaH-cD

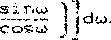
e

+

tga In

si n<, a> »<-O

COSO)

Для определения константы с зададим е=е с о< е ^^/й) в точке а, для которой ось on перпендикулярна оси ох (в этой точке происходит касание со связью 7 при минимальном диаметре шкива). При этом г=п/г - е_о$ ^=п/г -а, так что ы=п/г - а - е^ (рис.4).

Определив с помощью этих значений константу с, получим sinCa+e Dsi nv. a>+a)

= ^ - a - ci + cga In--------s--

2                       cos6 cosa)

Присоединив к (4) равенство (см. (i)).

si nC cu+cO имеем параметрические уравнения искомой кривой, пределах "рабочей” части кривой ав меняется Шд=,7./2-е^-а в точке а до значения

C4D

Парметр ш в от значения

arcsin -г - Ct d

Рис, 4

в точке, в, которое определяется из (?) при р-о^а и соответствует максимальному диаметру шкива. При этом не исключается и значение «>=о

Выражая из <з) и подставляя в (4), получаем уравнение кривой в виде с=еср>:

os -- + t got 1 n

В пределах "рабочей” части кривой р меняется от p_a=_C7-™q До рр-а. Будем считать, что a«icos6. Тогда р_к<  г_в и и> > а<_в.

Выскажем некоторые соображения относительно формы найденной кривой. С угон целью заметим, что

Г.К»                            с t gC сб+сО 5: G.

Поэтому из (7) сл/дуит, что е принимает наибольшее значение етах при о=о, т.е. при

S1 по b соответствующей точке м, луч r*m идет по касательной. При этим,как следует из (4),

г tga in---

s i пС а+в } s.i па

Исходя из требуемого вида рабочей поверхности, будем считать, что ^в<<’- Это обеспечивается неравенством dsiпо.

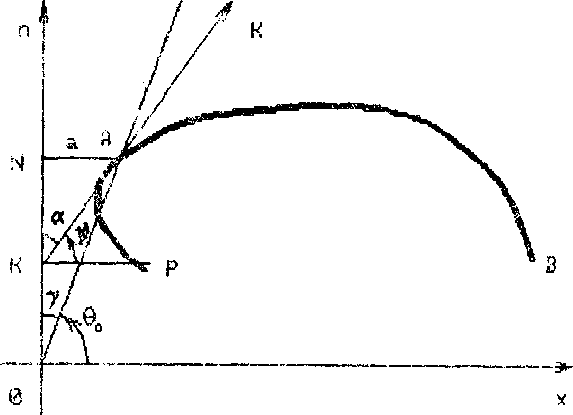
Вид кривой в пределах от а до в зависит от того, лежит ли точка м между а и в или нет. А это, в свою очередь, зависит от величины е_о, т.е. от начального положения связи ^.

В случае, изображенном на рис.4, е_о> п/2 - « =_v„ т.е. -д^о. Т.к. ^хш , то при движении точки по кривой от а к в ее полярный угол е убывает (см.(7)). При этом точка и находится между точками в и а, т.е. вне "рабочей" части кривой.

Если б_=п,г - с (рис.5), то «_А=о, т.е. ^е_тач^т8_с. ^{1 м}_о совпадает с а), в убывает от ©_о до е_в.

Наконец, если о < пег - а (рис.в), то ш_д>о, так что точка м лежит между див. в этом случае е при движении точки ст а до м, возрастает, а от м^ до в - убывает.

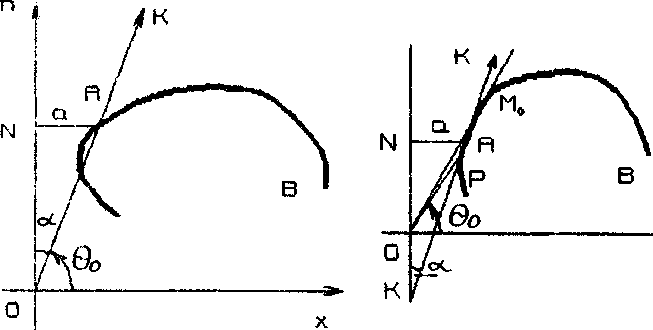
Рис. 5

Рис. В

В заключении обсудим вопрос о соотношениях между параметрами задачи а, о, о, и о. Выше были приняты условия к.юа', и as-is, по. Очевидно, если е ' » . о (рис.4), то второе условие вытекает из первою. Если о < “ « (рис.В), то первое следует из втори-о, а если п 'г « (рис.5), то оба условия совпадают. Таким образом, в каждом случае достаточно обеспечить одно из этих условий.

Кроме того, по практическому смыслу задачи должно бытп е -о.Значение е_н получается из (о) при ;>=<>. Это дает еще одно соотношение между а, •», е и а. Заметим, что, как следует из (о), е - «у при р * », т.е. вся кривая представляет собой бесконечно расширяющуюся спираль с началом в точке в и (коконечным множеством витков вокруг полюса о. Поэтому при заданных <, «, и о величина а не до.лжна быть слишком большой.

Одесский i|оли|ухнический и нс титут

Перм ский т'осударств онны й универюитсл¹

Ин|.‘ин1, iiivif'iHi'. i'H'Ich и проц. Nai е^ , 1904