Signals transmission by invariant method with further non-linear processing under weak correlation

The analysis of the qualitative parameters of the invariant system with non-linear processing of the readings of the sub-carrier under weak correlativity of the noise readings is carried out. The analytical expression of calculation of the probability density of the invariant estimation is found. All this allows to use the given structure for qualitative transmission of information.

In papers [1–5] the invariant systems of transmission of information having different probabilities of pairwise transition were investigated.

It should be pointed out that the mentioned above invariant systems have appreciably better characteristics in comparison with the classical systems of amplitude modulation under complex influence of noise.

The advantage in noise immunity of the invariant systems is explained by the fact that the modulating parameter is included in the relation of energies of informative and training signals.

However, it should be pointed out that the search for construction of such invariant systems is not stopped. The given paper is devoted to the further investigation of characteristics of the invariant system using square-law characterized detection, that is non-linear processing of signals.

Statement of Purpose. There is a channel of communication, limited by the frequencies f_h and f_l . Temporal dynamics of the channels with variable parameters can be conventionally divided into the intervals of stationarity. Consider the reception of the informative and training signals within the extracted intervals of stationarity. Within the abovementioned intervals the influence of multiplicative noise is described by the constancy of the coefficient of transmission k ( t ) on a certain frequency. The algorithm of reception is determined by the carrying frequency, given as an average frequency of the channel, whose amplitude is modulated by the sub-carrier.

Each transmitting block will contain an informative part and a sequence of training signals S _tr. The quantity of the elements of the information sequence related to the quantity of the elements of the training sequence is equal to:

N inf : N tr = 3:3.

Due to the changing of parameters of the communication channel to informative and training signals, the additive noise is interfering.

The Solution of the Stated Problem. On the receiving side the training signals are averaged and used for demodulation of the informative part of the block and for reduction of additive noise influence of the communication channel.

In figure 1 the structure of the receiving part of the invariant relative amplitude modulation is represented. Such kind of structure contains a synchronous detector (multiplier, PLL and LPF) and a special calculator.

Due to the equal influence of multiplicative noise on both parts of each transmitted block, the algorithm of demodulation of the reception signals with the chosen way of signals processing will consist in calculation of the invariant estimation.

Since non-linear square-law characterized algorithm is used in calculation of the estimation of the invariant, the following relationship is true:

N

X ( k ■ INV 1 ■ S ( i ) + ^ ( i ) )

• INV * ² = — ^n------------------- S t (1)

7 LZ ( ^k ■ ^S» ■^{S (} j ⁾⁺n⁽ m , j ) )

L m = 1 j = 1

In the numerator of the expression (1) there is a sum of N squares of instantaneous readings of the signal of information impulse. The information signal is formed by the sub-carrier of the kind

S (i ) = A sin (2 n f_s ■At ■ i ) , where A is amplitude; f_s is frequency of oscillations of the sub-carrier; A t is digitization interval and is equal to the following expression:

C(i ) = k■ INV l ■ SU ) + ^( i ) , where k ■ INV / ■ S (i ) is instantaneous reading of the signal of the information part of the block, coming from the channel; x( i ) – additive noise readings, distributed according to the normal law; k is the coefficient of transmission of the communication channel on the interval of stationarity.

In the denominator of the expression (1) there is a sum of N squares of instantaneous readings of the signal of training impulse, formed by the sub-carrier

G (m ) = k ■ S tr ■ S (i ) + n ( m , j ) , where n ( m , j ) is noise in m -realization of the training signal, distributed according to the normal law; L is the quantity of accumulation G ( m ).

Without loss of generality it is supposed that S tr = 1. If S tr * 1 then all the initial parameters, namely INV l and g₂ (root-meansquare deviation of the noise 2( i ), n( m ■ j )) can be scaled by the quantity S _tr .

In accordance with the restrictions introduced, formula (1) will be as follows:

N

£ ( k ■ INV i ■ S ( i ) + 2 ( i ) )

^INV * 2 =       -------------------- 2 = B ■    ⁽²⁾

7 ££ ( k ■ ^S ( j ⁾⁺ n ( m ■ ^j ) )

L m = 1 j = 1

where variables are described above.

Let us assume that the occasional quantities 2(i) and n(m■ j) are equally distributed according to the normal law with the zero mathematic expectation and dispersion g22. Besides, it is supposed that in each block only the next occasional quantities are dependent. Then corr (2( i\ 2( i-1) ) =

= corr(n(m■ j)■ n( m■ j-1 )) = R■ where R is the coefficient of correlation.

All the other occasional quantities entering each receiving block will be independent. To realize this model, it is necessary to have

are calculated for the squares of invariants. The threshold value z _thr in the expression (3) is also squared. The shifted squares of the invariants in the formula (3) are marked as INV ₁ ² INV _i ² .

On the basis of the expression (2) mathematic expectation and dispersion of instantaneous values and are calculated. Mathematic expectation of the numerator is equal to[7]:

N mA = £(k2 INVl2 S(i)2 +g2).

i = 1

Mathematic expectation of the denominator is [7]:

N mB =£(k2S(i)2 +g2).

i = 1

Dispersion of the numerator is equal to [7]:

N

DA = 4 k2 INVl2 g 2 £ S2 (i)+2 Ng 4 + i=1

N - 1

+ 8 £ k ² INV l ² S ( i ) S ( i +1 ) g ² R + 4 ( N -1 ) R ² g 2 .

i = 1

Dispersion of the denominator is equal to [7]:

I R l <  VV2 .

Let us use the known approach of estimation of pairwise transition probability, described by the formula of average probability [6]

z 2_r                      -

P _tr = p J w i ( z ) dz + P i J w , ( z ) dz ■      (3)

0                              zt2hr where Ptr is the probability of transition of INV12 to INVi2 and vice versa; 1 is the probability of appearing INV12; iisthe probability of appearing INVi2.

The first integral is probability of appearing INV _i ² when INV ₁ ² is sent.

The second integral is probability of appearing INV ₁ ² when INV _i ² is sent.

z ² _thr is the threshold value, necessary to calculate P _tr ; with the known ₁ and _i.

It is calculated by the best bias estimation using minimization P _tr on z ² _thr .

Having unknown ₁ and _i we choose ₁ = _i = 0,5.

From analysis (3) it is evident that to calculate P _tr itis necessary to know the analytical expression W ₁ ( z ) and W_i ( z ) of the density of probability of invariant estimation.

At non-linear processing and calculation of quantities of the invariants the shift appears. This shift is stipulated by the fact that in the formula (3) the quantities W ₁ ( z ) and W_i ( z )

D - = L

4 k ² g ² £ S ² ( i ) + i = 1

+8 k ² g ² R £ S ( i ) S ( i + 1 ) +

+2 N g ⁴ + 4 ( N -1 ) R ² g ⁴

.

The calculation of the quotient of two accidental values is made on the basis of the formula given below [7]:

r

W ( z )= [-------- x

-L ^{2 nG} A ^g b

( zx - m A ) ²      ( x - m - ) 2

x e     ^2g A e ^2g b Xx\dx ■

where g^ and g_b are calculated using expressions (6) and (7)₅ m_A and m_B are calculated using expression (4) and (5).

It should be noted that in the formula (3) INV ₁ is used calculating W ₁ ( z ), and INV _i is used calculating W_i ( z ). The value of the pairwise probability P _tr was calculated using the method of numerical integration. The number of accumulations with averaging is equal to 40.

The data obtained are restricted by the first six pairs of compared invariants, when INV ₁ =1, INV _i =2;3;4;5;6;7.

The probability of the pairwise transition was calculated by the values h -relations of signal/noise with the help of the formula defined by the relation of the signal intensity to the noise intensity

k ² INV l ² a

N G ²

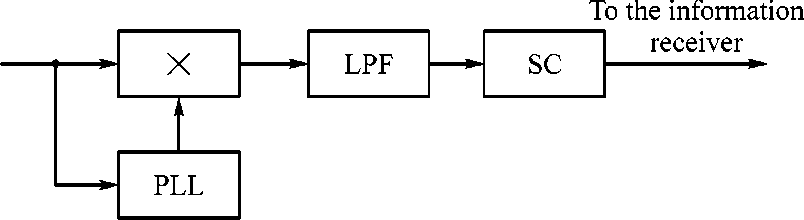
Fig. 1. Structural circuit of invariant system of information transmission: PLL is a phase-lock loop; LPF is a low-pass filter

The peculiarity of any invariant system based on the principle of the invariant relative amplitude modulation is amplitude modulating signals formed by INV _l and S _tr transmitted through the channel.

The transmission of these signals is provided on the basis of classical algorithms of information processing and has low noise immunity. Only after processing of these signals in accordance with the algorithm of the quotient of the expression (2) we obtain the estimation of the invariant which is really a number, not a signal.

Curve2infigures2and3 corresponds to the probability of error P_er in classical systems, being an analogue of the probability of pairwise transition, and is calculated by the known formulas [6].

As we can see from figures 2 and 3 the probability of pairwise transition in invariant system is determined by the quantity (10–1...10–18). At the same values signal/noise probability of inaccurate reception of a single symbol in the classical systems is in the limits (10–1...10–5).

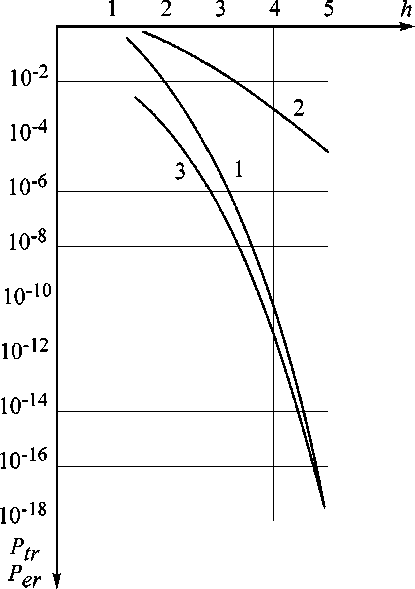
Fig. 2. Noise immunity of invariant system under the absence of multiplicative noise and INV₁ =1; INV _i =2;3;4;5;6; 7 Curve 1 is the probability of pairwise transition under weak correlation of readings of the noise and non-linear processing of signal readings Curve 2 is the probability of error of classical AM Curve 3 is the probability of pairwise transition under non-correlativity of noise readings and using extended synchronous detector

The carried out analysis shows that the invariant system of information transmission under additive noise with non- correlated readings has high noise immunity. The probability of error of the classical algorithm with amplitude modulation is at least by two orders greater than the probability of pairwise transition in invariant system.

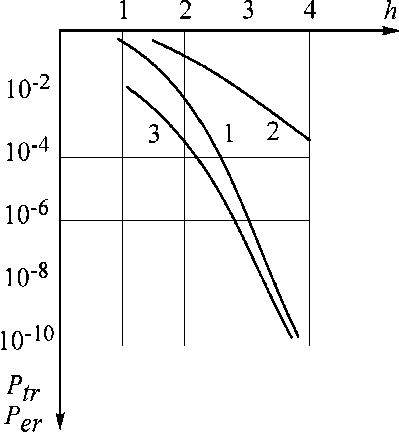
Fig. 3. The noise immunity of the invariant system under multiplicative noise and k = 0,7; INV1 =1; INVi =2;3;4;5;6; 7 Curve 1 is the probability of pairwise transition under weak correlativity of the readings of noise and non-linear processing of signal readings Curve 2 is the probability of error of the classical AM Curve 3 is the probability of pairwise transition under non-correlativity of the readings of the noise and application of the extended synchronous detector

We should like to emphasize that the system with the square-law characterized non-linear processing is much simpler in realization in comparison with the invariant systems, developed by the authors earlier [1–5]. Simplification presupposes that in the developed above algorithm the extended synchronous detection is not required. Therefore, the system can be used in telecommunication systems, telecontrol systems and other systems requiring high level of immunity to noise.