Сила Хмельника

В [1] показано, что силы Лоренца и Ампера могут быть определены как следствия существования потока электромагнитного импульса и закона сохранения импульса. При этом они определяются в виде (в системе СИ)

F = V • 5 • 4ЁЙ!c ,

где

S - плотность потока энергии,

V - объем тела, пронизываемого потоком электромагнитного поля,

ε - относительная диэлектрическая проницаемость тела,

• µ - относительная магнитная проницаемость тела,

• c - скорость света в вакууме.

2.    Двигатель Фарадея

На основе этой формулы можно утверждать, что существует еще одна сила, которую для краткости назовем силой Хмельника (если, конечно, никто еще не рассматривал эту силу). В частности, она может быть силой Лоренца или силой Ампера. Но в других случаях она не эквивалентна этим силам. Рассмотрим некоторые такие случаи.

Наиболее яркий пример такой силы можно наблюдать в конструкции, изображенной на следующем рис. 1. "Изобретатель данного мотора взял дисковый неодимовый магнит с никелевым покрытием, намагниченный по оси, к нему в центре примагнитил шуруп с острым концом, а этот конец примагнитил к плюсу круглой батарейки. Минусовой вывод батарейки он соединил тонким проводом (как щетка) с цилиндричской поверхностью магнита. Таким образом, между острием шурупа и плюсовым выводом образовался подшипник с очень малым трением. Когда минус батареи был соединен с окружностью магнита, магнит закрутился сразу и в течении пары секунд развил скорость порядка 15,000 об/мин, после чего за счет дисбалланса сорвался с шурупа и улетел!". Цитата и рис. 1 взяты из [2], но каждый может легко повторить такой эксперимент. Ранее в [3] было дано краткое объяснение этого эксперимента.

Рис. 1.

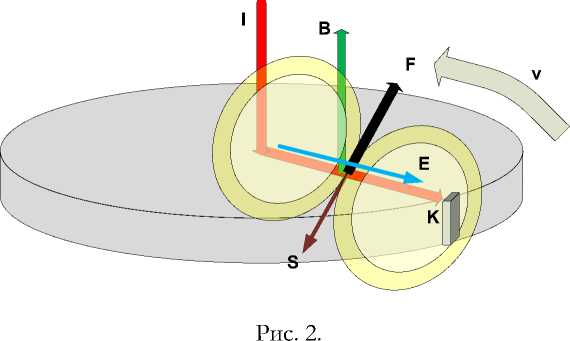
В сущности, это – частный случай двигателя Фарадея – см. рис. 2. В нем имеется электропроводящий магнит с индукцией B , линия тока I , проходящего по оси вращения (вертикальному шурупу на рис. 1), радиусу магнита и неподвижный контакт K . На токопроводящем радиусе имеется электрическая напряженность

E = j ρ ,                                              (2)

где j - плотность тока, ρ - удельное сопротивление. Магнитная напряженность H пропорциональна индукции B . Векторы этих напряженностей взаимно перпендикулярны и поэтому возникает поток электромагнитной энергии с плотностью

S = EH ,                                            (3)

показанный на рис. 2 окружностями в плоскости магнита. Заметим, что этот поток возникает в статическом электромагнитном поле. Этот поток создает силу F , вращающую магнит со скоростью v . Эта сила не является ни силой Лоренца, ни силой Ампера.

3.    Мысленный эксперимент Тамма

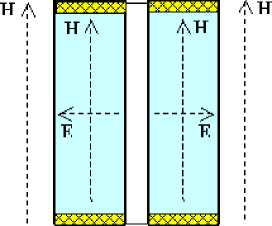
В [4] Тамм описывает следующий мысленный эксперимент – см. рис. 3. Рассматривается цилиндрический конденсатор, помещённый в однородное магнитное поле Н , параллельное его оси. В пространстве между обкладками конденсатора, помимо магнитного, существует также и радиальное электрическое поле напряжённости E , созданное заряженным конденсатором. В пространстве между обкладками конденсатора в статическом электромагнитном поле существует вектор Пойнтинга (3). Линии вектора Пойнтинга, т. е. линии потока энергии, представляют собой концентрические окружности, плоскости которых перпендикулярны к оси конденсатора.

N

Рис. 3.

4.    Эксперимент Грехема и Лахоза

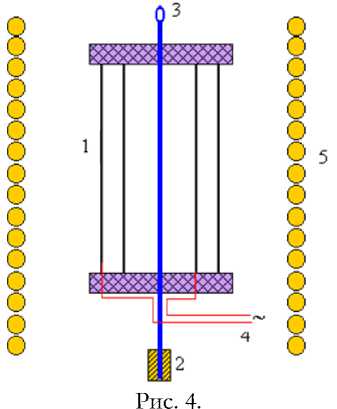
Схема эксперимента приведена на рис. 4, где

• 1    - цилиндрический конденсатор,

• 2    - торсионно-осцилляторная подвеска,

• 3    - зеркальце,

• 4    - радиально расположенные провода для подачи переменного напряжения на пластины,

• 5    - сверхпроводящий соленоид.

5 . Мысленный эксперимент Иванова 3.    Предлагаемая конструкция

Авторы пишут: "Наша программа измерения сил, связанных с электромагнитным импульсом на низких частотах в веществе достигла кульминации в первом прямом наблюдении свободного электромагнитного момента импульса, создаваемого квазистатическими (неволновыми) независимыми полями E и B в пространстве между пластинами цилиндрического конденсатора. Чтобы зарегистрировать его (конденсатора) движение использовалась резонансная подвеска. Наблюдаемые изменения момента импульса согласуются с классической теорией в пределах ошибки ~ 20%. Это наводит на мысль, что вакуум есть место, где что-то движется, при наличии статических полей, обладающих ненулевым вектором Пойнтинга, как и предвидели Максвелл и Пойнтинг. "

Эксперименты Тамма, Грэхема и Лахоза обсуждает Иванов в [6] (откуда взяты иллюстрации и перевод статьи [5]). Из них, по его мнению, следует, что "момент импульса вещества и поля не сохраняется". Позднее в [7] он предлагает конструкцию, изображенную на рис. 5. Он полагает, что его конструкция будет двигаться только при переменном напряжении. Его доказательство построено "на основании законов сохранения импульса, энергии и принципа относительности, согласно которым такое движение осуществляется благодаря силовому и энергетическому взаимодействию с физическим вакуумом (эфиром)".

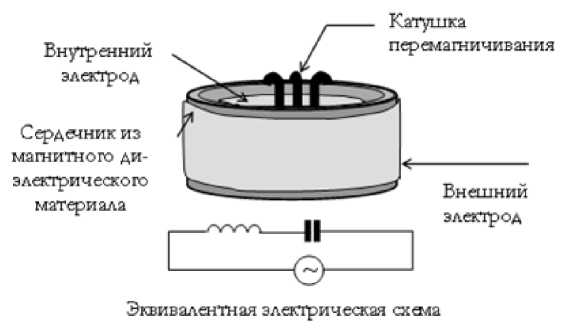
Рис. 6.

Все вышеперечисленные эксперименты не могут быть объяснены силами Лоренца или Ампера, но легко объясняются силами (1). Наиболее отчетливо это можно показать на предлагаемой далее конструкции.

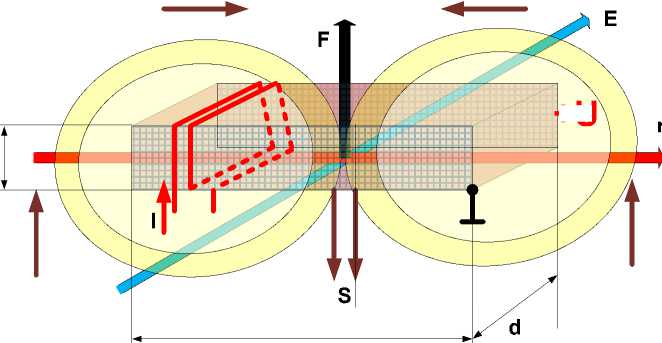
Рассмотрим рис. 7, где изображено тело, находящееся внутри соленоида с постоянным током I . Тело имеет обкладки-электроды, находящиеся под постоянным напряжением U . При этом в теле создается стационарное электромагниное поле с электрической E и магнитной H напряженностями. Возникает поток электромагнитной энергии с плотностью (3), показанный на рисунке окружностями. Можно представить его в виде двух сфер, объединяющихся в теле и пронизывающих его в вертикальном направлении. Этот поток создает силу (1), действующую на тело.

h

+U

L

Рис. 7.

Рассмотрим подробнее расчет силы (1), используя для этого обозначения размеров тела, показанные на рис. 3: L, d, h . Имеем:

E = U / d , H = Iw / L , V = hdL .

При этом

F = V • E • H • ^ёц!c ,

или

F = hUIw ЛС c .

Пример .       Пусть в системе СИ

I = 1, _e = 4, c = 3 • 10 8 , U = 30000, I = 20, h = 0.2, w = 100 .

Тогда F = 0.2 • 30000 • 20 - 10074 ^ 1/3 - 10 8 = 0.08 [ V ] .

Таким образом, устройство обещает быть реализуемым . Автор приглашает экспериментаторов проверить появление силы Хмельника и дополнить ее название своим именем.